Программирование на языке Python

1. Программирование на языке Python

1
Программирование
на языке Python
Лекция 7. Процедуры и
функции. Рекурсия
Заманова С.К.

2. Что такое подпрограмма?

2
Что такое подпрограмма?
Подпрограмма – это отдельная функционально независимая часть программы, имеющая имя и решающая
отдельную задачу.
Подпрограммы:
✓ избавляют от необходимости многократно повторять в
тексте программы аналогичные фрагменты;
✓ улучшают структуру программы, облегчая ее понимание;
✓ позволяют распределять большие задачи между
несколькими разработчиками или стадиями проекта;
✓ повышают устойчивость к ошибкам программирования и
непредвидимым последствиям при модификациях
программы

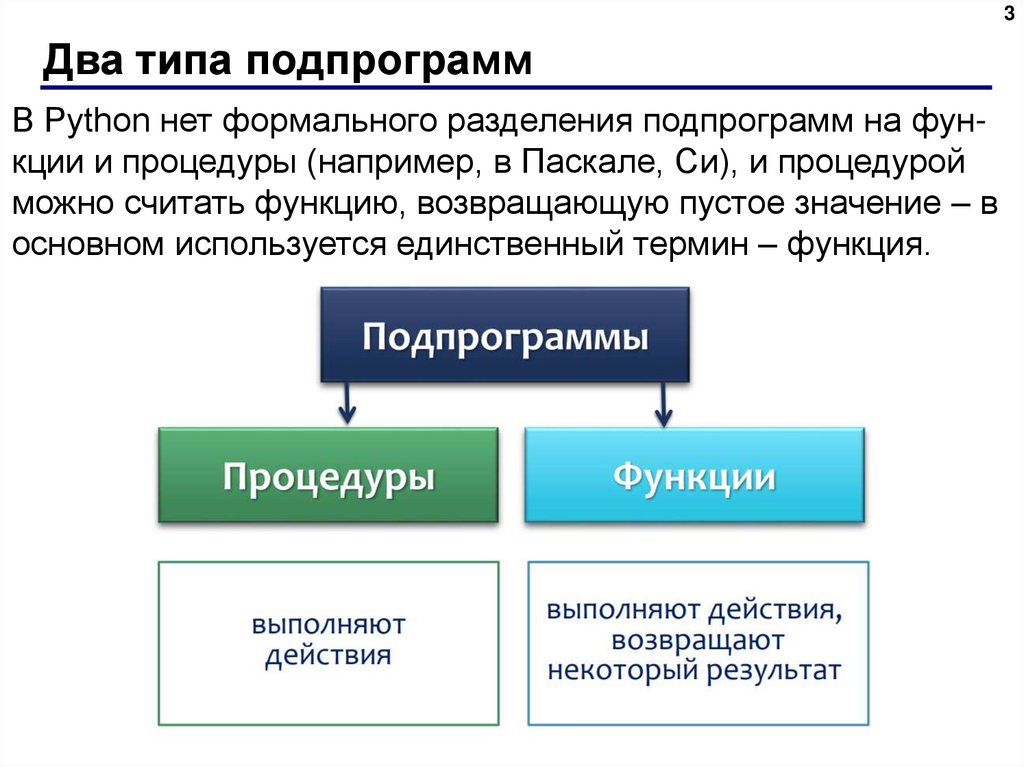
3. Два типа подпрограмм

3
Два типа подпрограмм
В Python нет формального разделения подпрограмм на функции и процедуры (например, в Паскале, Си), и процедурой
можно считать функцию, возвращающую пустое значение – в
основном используется единственный термин – функция.

4. Что такое процедура?

4
Что такое процедура?
Процедура – вспомогательный алгоритм, который выполняет
некоторые действия.
• текст (расшифровка) процедуры записывается до её вызова
в основной программе
• в программе может быть много процедур
• чтобы процедура заработала, нужно вызвать её по имени
из основной программы или из другой процедуры.
Общий вид процедуры:
define
имя
определить
процедуры
def name_procedury(параметры):
тело процедуры
Параметр – это
переменная, от значения которой зависит
работа подпрограммы;
если параметры не нужны – ставят пустые ()

5. Вызов процедуры

5
Вызов процедуры
При вызове процедуры нужно в скобках передать ей
фактические значения параметров.
Аргумент – это значение параметра, которое передаётся
подпрограмме при её вызове.
Аргументом может быть не только постоянное значение
(число, символ), но также переменная, и даже
арифметическое выражение.
•name_procedury() или
•name_procedury(n) или
•name_procedury(a, b, c, d)

6. Зачем нужны процедуры?

6
Зачем нужны процедуры?
print ( "Ошибка программы" )
много раз!
Процедура:
define
определить
def Error():
print( "Ошибка программы" )
n = int ( input() )
if n < 0:
вызов
Error()
процедуры

7. Процедура с параметрами

7
Процедура с параметрами
Задача. Вывести на экран запись целого числа (0..255) в
8-битном двоичном коде.
много раз!
Алгоритм:
178 101100102
? Как вывести первую цифру?
7
6 5 4
3 2 1
0
n:= 1 0 1 1 0 0 1 02
n // 128
разряды
n % 128
? Как вывести вторую цифру?
n1 // 64

8. Процедура с параметрами

8
Процедура с параметрами
Задача. Вывести на экран запись целого числа (0..255) в
8-битном двоичном коде.
Решение:
n
k
вывод
k = 128
178
128
1
while k > 0:
print ( n // k,
end = "" )
n=n%k
k = k // 2
178 10110010
зависит
! Результат
от n!
50
50
18
64
32
16
0
1
1
2
2
2
8
4
2
0
0
1
0
0
1
0
0

9. Процедура с параметрами

9
Процедура с параметрами
Параметры – данные, изменяющие
работу процедуры.
def printBin( n ):
k = 128
while k > 0:
локальная
переменная
print ( n // k, end = "" )
n = n % k;
k = k // 2
printBin ( 99 )
Несколько параметров:
def printSred( a, b ):
print ( (a + b)/2 )
значение параметра
(аргумент)

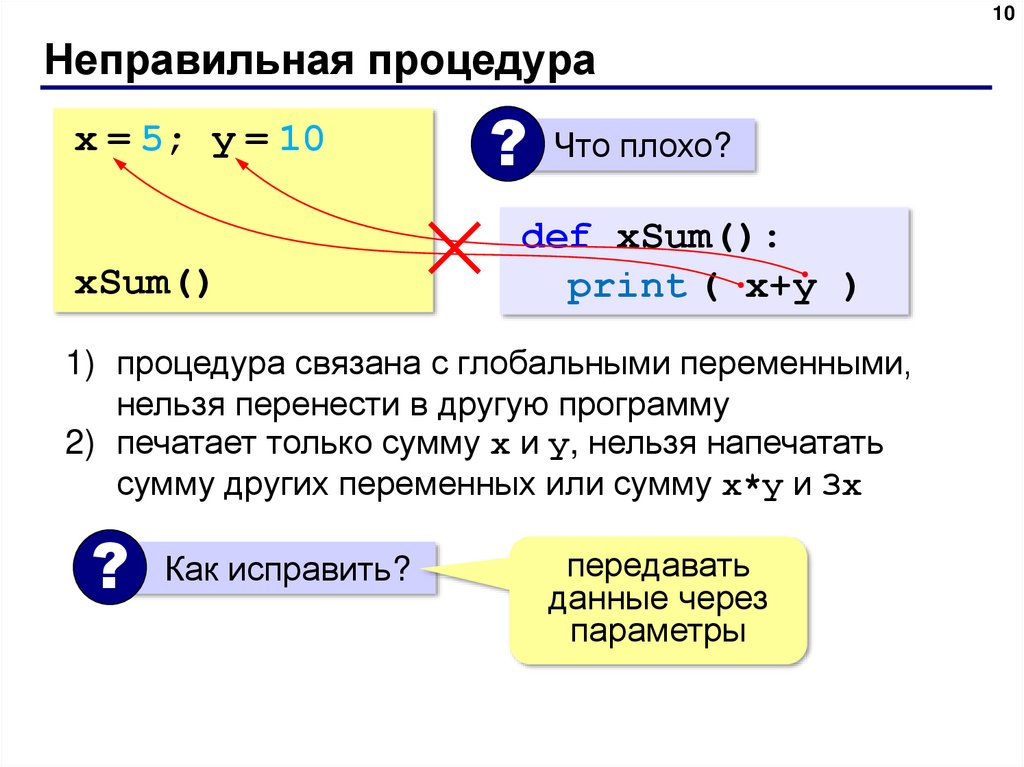
10. Неправильная процедура

10
Неправильная процедура
x = 5; y = 10
def sum():
print ( x+y )
xSum()
? Что плохо?
def xSum():
print ( x+y )
1) процедура связана с глобальными переменными,
нельзя перенести в другую программу
2) печатает только сумму x и y, нельзя напечатать
сумму других переменных или сумму x*y и 3x
? Как исправить?
передавать
данные через
параметры

11. Правильная процедура

11
Правильная процедура
Глобальные:
x
y
5
10
z
w
17
3
def Sum2(a, b):
print ( a+b )
x = 5; y = 10
Sum2( x, y )
z=17; w=3
Sum2( z, w )
Sum2( z+x, y*w )
Локальные:
a
b
17
22
5
10
30
3
1) процедура не зависит от глобальных
переменных
2) легко перенести в другую программу
3) печатает только сумму любых выражений
15
20
52

12. Задачи

12
Задачи
«A»: Напишите процедуру, которая принимает параметр –
натуральное число N – и выводит на экран линию из N
символов '–'.
Пример:
Введите N:
10
---------«B»: Напишите процедуру, которая выводит на экран в
столбик все цифры переданного ей числа, начиная с
первой.
Пример:
Введите натуральное число:
1234
1
2
3
4

13. Задачи

13
Задачи
«C»: Напишите процедуру, которая выводит на экран
запись переданного ей числа в римской системе
счисления.
Пример:
Введите натуральное число:
2013
MMXIII

14. Программирование на языке Python

14
Программирование
на языке Python
Функции

15. Что такое функция?

15
Что такое функция?
Функция – это вспомогательный алгоритм, который возвращает
значение-результат (число, символ или объект другого типа).
Общий вид функции:
define
имя
определить
функции
def name_function(параметры):
тело функции
return (результат)
Выражение, стоящее после ключевого слова return будет
возвращаться в качестве результата вызова функции.
Результат вызова функции можно:
✓ присвоить переменной,
✓ использовать его в качестве операндов математических
выражений, т.е. составлять более сложные выражения.

16. Сумма цифр числа

16
Сумма цифр числа
Задача. Написать функцию, которая вычисляет сумму цифр
числа.
сумма = 0
Алгоритм:
пока n != 0:
сумма += n % 10
n = n // 10
Программа:
def sumDigits( n ):
sum = 0
while n!= 0:
sum += n % 10
n = n // 10
return sum
# основная программа
print ( sumDigits(12345) )
передача
результата

17. Использование функций

17
Использование функций
x = 2*sumDigits(n+5)
z = sumDigits(k) + sumDigits(m)
if sumDigits(n) % 2 == 0:
print ( "Сумма цифр чётная" )
print ( "Она равна", sumDigits(n) )
! Функция, возвращающая целое число, может
использоваться везде, где и целая величина!
Одна функция вызывает другую:
def middle ( a, b, c ):
mi = min ( a, b, c )
ma = max ( a, b, c )
return a + b + c - mi - ma
вызываются
min и max
? Что вычисляет?

18. Задачи

18
Задачи
«A»: Напишите функцию, которая находит наибольший
общий делитель двух натуральных чисел.
Пример:
Введите два натуральных числа:
7006652 112307574
НОД(7006652,112307574) = 1234.
«B»: Напишите функцию, которая определяет сумму
цифр переданного ей числа.
Пример:
Введите натуральное число:
123
Сумма цифр числа 123 равна 6.

19. Задачи

19
Задачи
«C»: Напишите функцию, которая «переворачивает»
число, то есть возвращает число, в котором цифры
стоят в обратном порядке.
Пример:
Введите натуральное число:
1234
После переворота: 4321.

20. Как вернуть несколько значений?

20
Как вернуть несколько значений?
def divmod ( x, y ):
d = x // y
d – частное,
m=x%y
m – остаток
return d, m
a, b = divmod ( 7, 3 )
print ( a, b )
# 2 1
q = divmod ( 7, 3 )
print ( q )
# (2, 1)
кортеж – набор
элементов

21. Задачи

21
Задачи
«A»: Напишите функцию, которая переставляет три
переданные ей числа в порядке возрастания.
Пример:
Введите три натуральных числа:
10 15 5
5 10 15
«B»: Напишите функцию, которая сокращает дробь вида
M/N.
Пример:
Введите числитель и знаменатель дроби:
25 15
После сокращения: 5/3

22. Задачи

22
Задачи
«C»: Напишите функцию, которая вычисляет
наибольший общий делитель и наименьшее общее
кратное двух натуральных чисел.
Пример:
Введите два натуральных числа:
10 15
НОД(10,15)=5
НОК(10,15)=30

23. Логические функции

23
Логические функции
Задача. Найти все простые числа в диапазоне от 2 до 100.
for i in range(2,1001):
if i
isPrime(i)
i -- простое
простое :
print ( i )
? Какой алгоритм?
функция, возвращающая
логическое значение
(True/False)
def isPrime ( n ):
k=2
while k*k <= n and n % k != 0:
k += 1
if k*k > n:
return (k*k > n)
return True
else:
return False

24. Логические функции: использование

24
Логические функции: использование
! Функция, возвращающая логическое значение,
может использоваться везде, где и логическая
величина!
n = int ( input() )
while isPrime(n):
print ( n, "– простое число" )
n = int ( input() )

25. Глобальные и локальные переменные

25
Глобальные и локальные переменные
• Переменные, которые введены в основной программе,
называются глобальными (общими). Их могут использовать
все подпрограммы (процедуры и функции).
• Переменные, которые используются только внутри процедуры или функции, называются локальными (местными). К
ним можно обращаться только внутри этой подпрограммы,
остальные подпрограммы и основная программа их не видят.
Такой прием называется инкапсуляцией (от латинского
«помещение в капсулу»).
• Локальная переменная создается только при вызове
процедуры или функции. Как только работа подпрограммы
будет закончена, все локальные переменные будут
удаляться из памяти.
• Имена локальных переменных в каждой подпрограмме
можно выбирать независимо от имён локальных переменных
других подпрограмм.

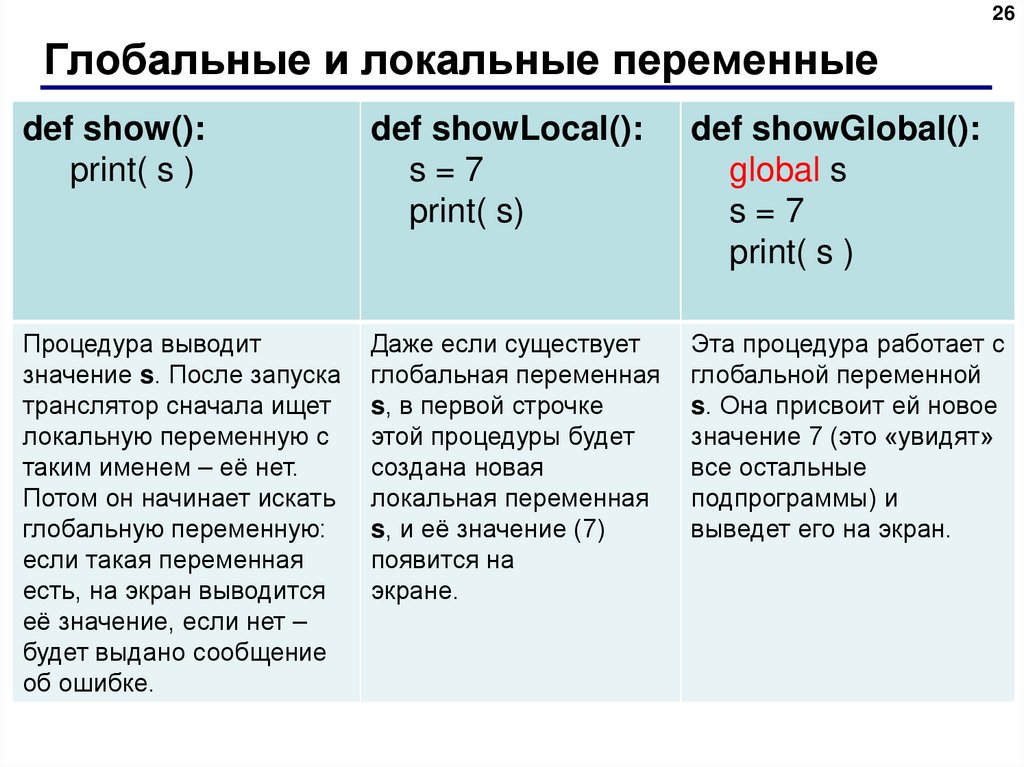
26. Глобальные и локальные переменные

26
Глобальные и локальные переменные
def show():
print( s )
def showLocal():
s=7
print( s)
def showGlobal():
global s
s=7
print( s )
Процедура выводит
значение s. После запуска
транслятор сначала ищет
локальную переменную с
таким именем – её нет.
Потом он начинает искать
глобальную переменную:
если такая переменная
есть, на экран выводится
её значение, если нет –
будет выдано сообщение
об ошибке.
Даже если существует
глобальная переменная
s, в первой строчке
этой процедуры будет
создана новая
локальная переменная
s, и её значение (7)
появится на
экране.
Эта процедура работает с
глобальной переменной
s. Она присвоит ей новое
значение 7 (это «увидят»
все остальные
подпрограммы) и
выведет его на экран.

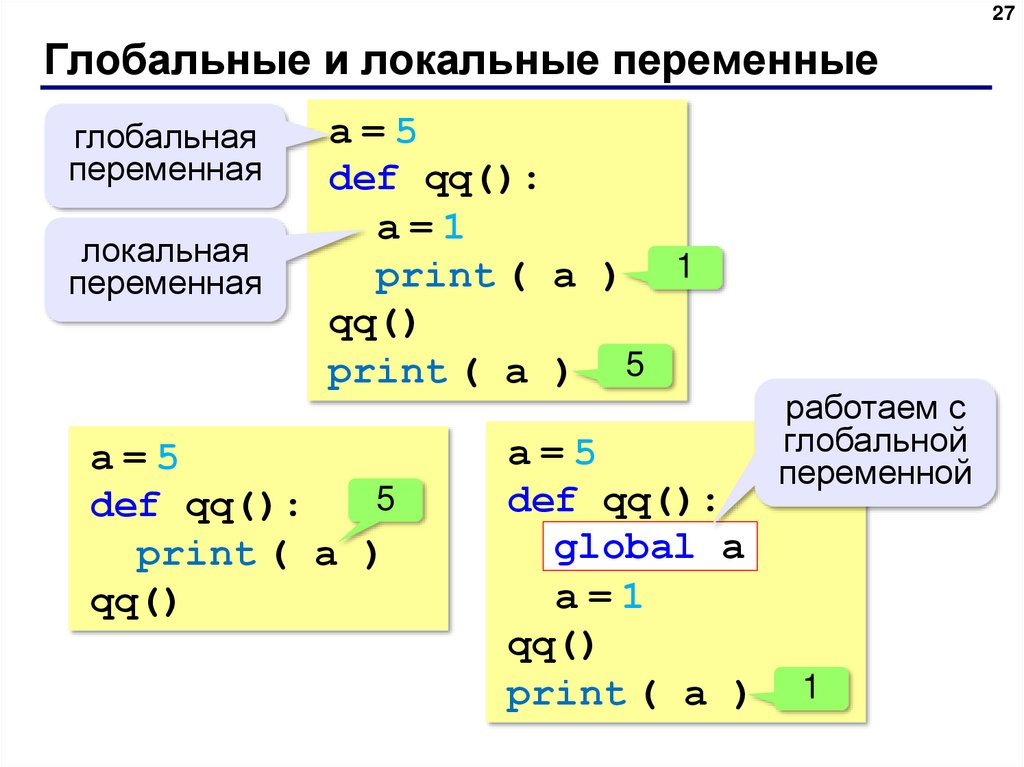
27. Глобальные и локальные переменные

27
Глобальные и локальные переменные
глобальная
переменная
локальная
переменная
a=5
def qq():
a=1
print ( a ) 1
qq()
print ( a ) 5
a=5
5
def qq():
print ( a )
qq()
a=5
def qq():
global a
a=1
qq()
print ( a )
работаем с
глобальной
переменной
1

28. Задачи

28
Задачи
«A»: Напишите логическую функцию, которая
определяет, является ли переданное ей число
совершенным, то есть, равно ли оно сумме своих
делителей, меньших его самого.
Пример:
Введите натуральное число:
28
Число 28 совершенное.
Пример:
Введите натуральное число:
29
Число 29 не совершенное.

29. Задачи

29
Задачи
«B»: Напишите логическую функцию, которая
определяет, являются ли два переданные ей числа
взаимно простыми, то есть, не имеющими общих
делителей, кроме 1.
Пример:
Введите два натуральных числа:
28 15
Числа 28 и 15 взаимно простые.
Пример:
Введите два натуральных числа:
28 16
Числа 28 и 16 не взаимно простые.

30. Задачи

30
Задачи
«С»: Простое число называется гиперпростым, если любое
число, получающееся из него откидыванием нескольких
цифр, тоже является простым. Например, число 733 –
гиперпростое, так как и оно само, и числа 73 и 7 –
простые. Напишите логическую функцию, которая
определяет, верно ли, что переданное ей число –
гиперпростое. Используйте уже готовую функцию
isPrime, которая приведена в учебнике.
Пример:
Введите натуральное число:
733
Число 733 гиперпростое.
Пример:
Введите натуральное число:
19
Число 19 не гиперпростое.

31. Программирование на языке Python

31
Программирование
на языке Python
Рекурсия

32. Рекурсия

32
Рекурсия
• Одной из идей процедурного программирования, которая
оформилась в начале шестидесятых годов ХХ века,
стало
активное
применение
в
практике
программирования некоторого метода, основанного на
организации серий взаимных обращений программ
(функций) друг к другу.
• Вопросы об эффективности использования данного
метода при разработке алгоритмических моделей
актуальны и в настоящее время, несмотря на
существование различных парадигм программирования,
создание новых и совершенствование существующих
языков программирования.
• Речь идет о рекурсивном методе в программировании,
который
рассматривается
альтернативным
по
отношению к итерационному.

33. Рекурсия

33
Рекурсия
• Рекурсия – это определение объекта через обращение к
самому себе (через такой же объект (или объекты), но с
другими параметрами).
• Рекурсивный алгоритм – это алгоритм, в описании
которого прямо или косвенно содержится обращение к
самому себе.
• Рекурсивная подпрограмма вызывает саму себя
напрямую или через другие подпрограммы.
• Количество вложенных вызовов функции или процедуры
• называется глубиной рекурсии. По умолчанию глубина
рекурсии в языке Python ограничена 1000 вызовов.
• Рекурсивная
программа
позволяет
описать
повторяющееся или даже потенциально бесконечное
вычисление, причем без явных повторений частей
программы и использования циклов.

34. Рекурсия

34
Рекурсия
• Прямое обращение функции к самой себе предполагает,
что в теле функции содержится вызов этой же функции,
но с другим набором фактических параметров. Такой
способ организации работы называется прямой
рекурсией.
• Например, чтобы найти сумму первых n натуральных
чисел, надо сумму первых (n-1) чисел сложить с числом
n, то есть имеет место зависимость: Sn=Sn-1+n.
Вычисление происходит с помощью аналогичных
рассуждений.
• Такая цепочка взаимных обращений в конечном итоге
сведется к вычислению суммы одного первого элемента,
которая равна самому элементу.

35. Рекурсия

35
Рекурсия
• При косвенном обращении функция содержит вызовы
других функций из своего тела. При этом одна или
несколько из вызываемых функций на определенном
этапе обращаются к исходной функции с измененным
набором входных параметров. Такая организация
обращений называется косвенной рекурсией.
• Например, поиск максимального элемента в массиве
размера n можно осуществлять как поиск максимума из
двух чисел: одно их них – это последний элемент
массива, а другое является максимальным элементом в
массиве размера (n-1). Для нахождения максимального
элемента
массива
размера
(n-1)
применяются
аналогичные рассуждения. В итоге решение сводится к
поиску максимального из первых двух элементов
массива

36. Рекурсия

36
Рекурсия
В математике существует множество рекурсивных функций,
которые для вычислений используют обращение к самой
себе только с другими аргументами.
Существуют два вида функций:
• Конечная рекурсивная функция – выполняется за
конечное количество рекурсивных вызовов, которые
приводят к частному или базовому варианту. Примером
такой функции является факториал числа, в котором для
аргумента со значением 0, задан базовый вариант
возвращаемого значения – 0! = 1;
• Бесконечная рекурсивная функция – для таких функций
не существует базового варианта, и они всё время
вызывают себя.
Примером служит непрерывная дробь f(x) = x / (f(x+2))

37. Примеры рекурсии

37
Примеры рекурсии
Факториал числа: n! = 1*2*…*n (0!=1)
• 0!=1,
• n! = n ⋅ (n-1)!
индуктивное определение
Рекурсия — это способ определения множества объектов
через само это множество на основе заданных простых
базовых случаев.
Формулу можно представить в таком виде:
n! = 1 * … * (n-2) * (n-1) * n,
т. е. каждый предыдущий множитель меньше на 1, чем последующий. Или в перевернутом виде:
n! = n * (n-1) * (n-2) * … * 1,
Функцию можно записать так:
•f(0) = 1;
•f(n) = f(n-1) ⋅ n.

38. Как работает рекурсия?

38
Как работает рекурсия?
Факториал:
1, N 1
N !
N ( N 1)!, N 1
def Fact(N):
print ( "->", N )
if N <= 1: F = 1
else:
F = N * Fact ( N – 1 )
print ( "<-", N )
return F
-> N = 3
-> N = 2
-> N = 1
<- N = 1
<- N = 2
<- N = 3
? Как сохранить состояние функции перед
рекурсивным вызовом?

39. Примеры рекурсии

39
Примеры рекурсии
Факториал числа:
Программа вычисления факториала числа с помощью цикла
n = int(input())
factorial = 1
for i in range(2, n+1):
factorial *= i
print(factorial)
Программа для рекурсивного вычисления факториала числа
def factorial(n):
if n == 1:
return 1
else:
return factorial(n - 1)*n
print(factorial(5))

40. Примеры рекурсии

40
Примеры рекурсии
Факториал числа:
Поток выполнения программы при n = 5:
Вызов функции fac(5)
fac(5) вызывает fac(4)
fac(4) вызывает fac(3)
fac(3) вызывает fac(2)
fac(2) вызывает fac(1)
fac(1) возвращает в fac(2) число 1
fac(2) возвращает в fac(3) число 1 * 2, т. е. 2
fac(3) возвращает в fac(4) число 2 * 3, т. е. 6
fac(4) возвращает в fac(5) число 6 * 4, т. е. 24
fac(5) возвращает число 24 * 5, т. е. 120 в основную ветку
программы
Число 120 выводится на экран

41. Примеры рекурсии

41
Примеры рекурсии
Факториал числа:
Такой рекурсивный алгоритм вычисления факториала имеет
два преимущества:
1.
Минимальное количество кода;
2.Полное соответствие математическому определению.
К недостаткам можно отнести ресурсы, которые используются
на рекурсивный вызов метода.
В стиле Python:
import math
print( math.factorial(4))
Результат: 24

42. Примеры рекурсии

42
Примеры рекурсии
Натуральные числа:
• 1 – натуральное число
• если n – натуральное число,
то n 1 – натуральное число
индуктивное
определение
Рекурсия — это способ определения множества
объектов через само это множество на основе
заданных простых базовых случаев.
Числа Фибоначчи:
• F1 F2 1
• Fn Fn 1 Fn 2 при n 2
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…

43. Примеры рекурсии

43
Примеры рекурсии
Числа Фибоначчи:
Программа вычисления чисел Фибоначчи с помощью цикла
fib1 = fib2 = 1
n = int(input())
print(fib1, fib2, end=' ')
for i in range(2, n):
fib1, fib2 = fib2, fib1 + fib2
Результат: 10
print (fib2, end=' ')
1 1 2 3 5 8 13 21 34 55
Рекурсивное вычисление n-го числа ряда Фибоначчи
def fibonacci(n):
if n in (1, 2):
return 1
else:
return fibonacci(n-1)+ fibonacci(n-2)
print(fibonacci(10))

44. Примеры рекурсии

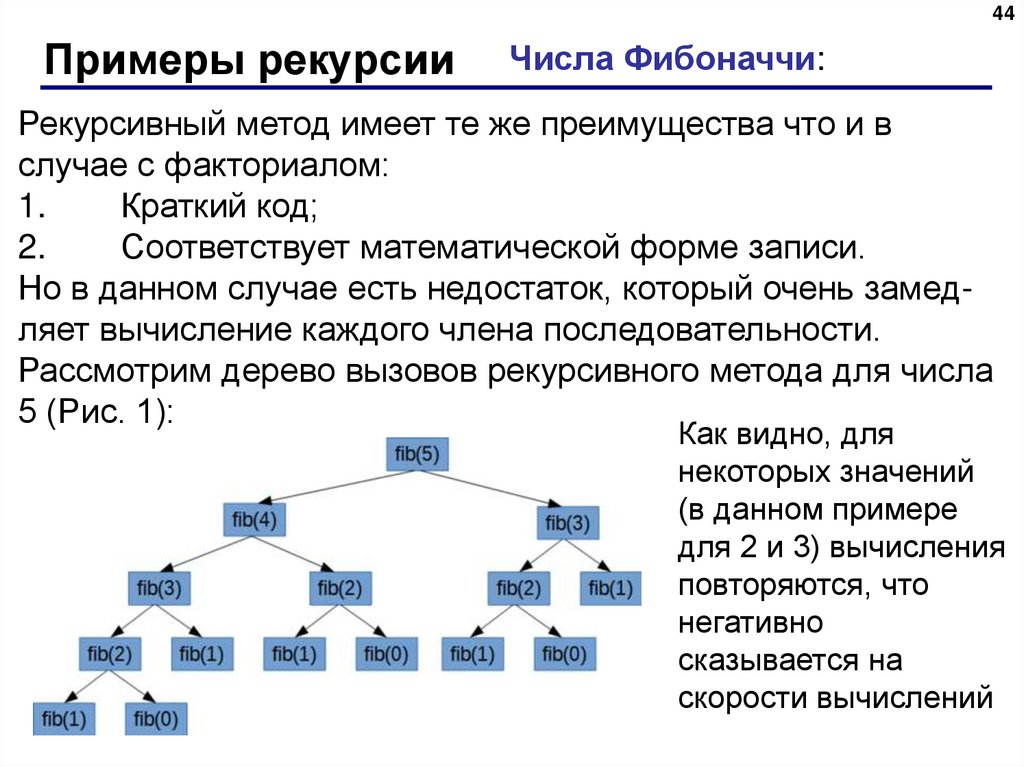
44
Примеры рекурсии
Числа Фибоначчи:
Рекурсивный метод имеет те же преимущества что и в
случае с факториалом:
1.
Краткий код;
2.
Соответствует математической форме записи.
Но в данном случае есть недостаток, который очень замедляет вычисление каждого члена последовательности.
Рассмотрим дерево вызовов рекурсивного метода для числа
5 (Рис. 1):
Как видно, для
некоторых значений
(в данном примере
для 2 и 3) вычисления
повторяются, что
негативно
сказывается на
скорости вычислений

45. Фракталы

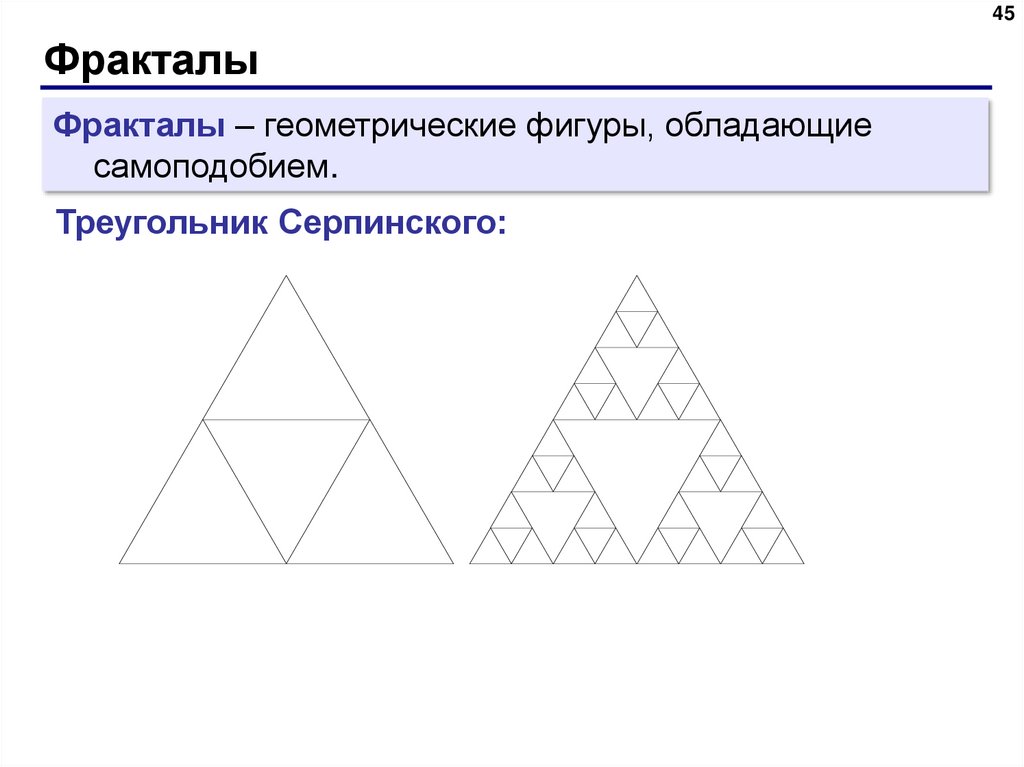
45
Фракталы
Фракталы – геометрические фигуры, обладающие
самоподобием.
Треугольник Серпинского:

46. Ханойские башни

46
Ханойские башни
1
2
3
• за один раз переносится один диск
• класть только меньший диск на больший
• третий стержень вспомогательный
перенести (n, 1, 3)
перенести (n-1, 1, 2)
1 -> 3
перенести (n-1, 2, 3)

47. Ханойские башни – процедура

47
Ханойские башни – процедура
сколько
откуда
куда
номер
def Hanoi ( n, k, m ): вспомогательного
рекурсия p = 6 - k - m
стержня (1+2+3=6!)
Hanoi ( n-1, k, p )
print ( k, "->", m )
Hanoi ( n-1, p, m )
рекурсия
? Что плохо?
! Рекурсия никогда не остановится!

48. Ханойские башни – процедура

48
Ханойские башни – процедура
Рекурсивная процедура (функция) — это процедура
(функция), которая вызывает сама себя напрямую или
через другие процедуры и функции.
def Hanoi ( n, k, m ):
if n == 0: return
p=6-k-m
Hanoi ( n-1, k, p )
print ( k, "->", m )
Hanoi ( n-1, p, m )
# основная программа
Hanoi( 4, 1, 3 )
условие выхода из
рекурсии

49. Вывод двоичного кода числа

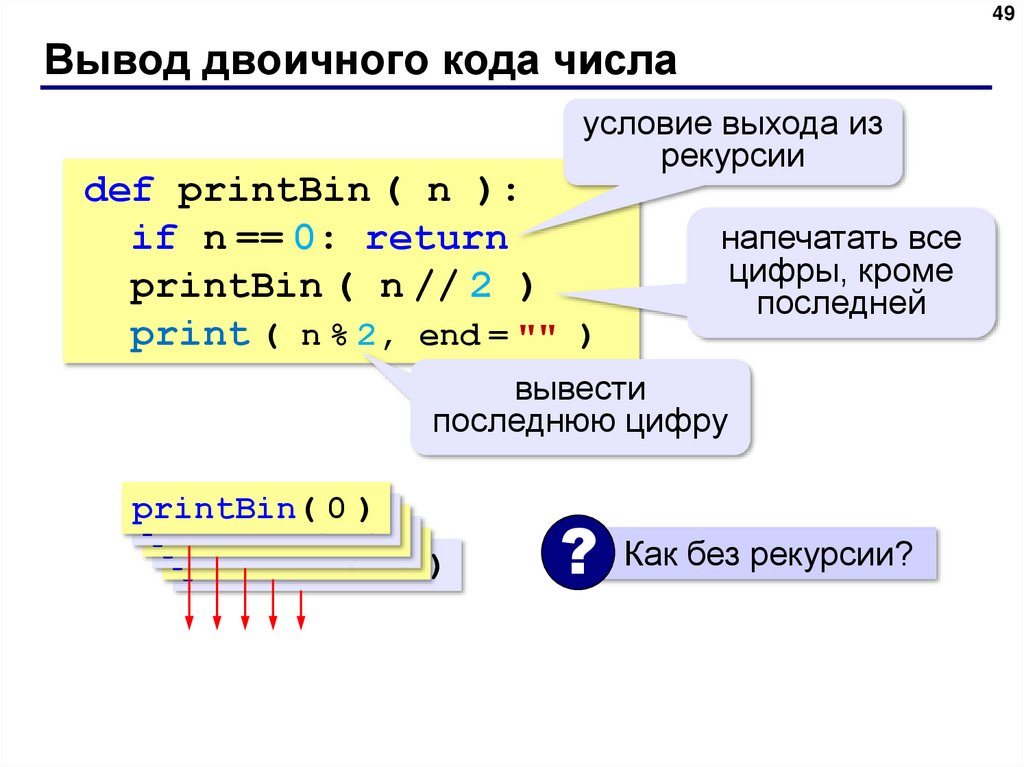
49
Вывод двоичного кода числа
условие выхода из
рекурсии
def printBin ( n ):
if n == 0: return
printBin ( n // 2 )
print ( n % 2, end = "" )
напечатать все
цифры, кроме
последней
вывести
последнюю цифру
printBin(
01))
printBin(
printBin(
24))
printBin(
printBin(
))
printBin(919
10011
? Как без рекурсии?

50. Вычисление суммы цифр числа

50
Вычисление суммы цифр числа
def sumDig ( n ):
sum = n % 10
последняя цифра
if n >= 10:
sum += sumDig ( n // 10 )
return sum
рекурсивный вызов
? Где условие окончания рекурсии?
sumDig( 1234 )
4 + sumDig( 123 )
4 + 3 + sumDig( 12 )
4 + 3 + 2 + sumDig( 1 )
4 + 3 + 2 + 1

51. Алгоритм Евклида

51
Алгоритм Евклида
Алгоритм Евклида. Чтобы найти НОД двух натуральных
чисел, нужно вычитать из большего числа меньшее до
тех пор, пока меньшее не станет равно нулю. Тогда
второе число и есть НОД исходных чисел.
def NOD ( a, b ):
if a == 0 or b == 0:
условие окончания
рекурсии
return a + b;
if a > b:
return NOD( a - b, b )
else:
return NOD( a, b – a )
рекурсивные вызовы

52. Задачи

52
Задачи
«A»: Напишите рекурсивную функцию, которая
вычисляет НОД двух натуральных чисел, используя
модифицированный алгоритм Евклида.
Пример:
Введите два натуральных числа:
7006652 112307574
НОД(7006652,112307574)=1234.
«B»: Напишите рекурсивную функцию, которая
раскладывает число на простые сомножители.
Пример:
Введите натуральное число:
378
378 = 2*3*3*3*7

53. Задачи

53
Задачи
«C»: Дано натуральное число N. Требуется получить и
вывести на экран количество всех возможных
различных способов представления этого числа в
виде суммы натуральных чисел (то есть, 1 + 2 и 2 + 1
– это один и тот же способ разложения числа 3).
Решите задачу с помощью рекурсивной функции.
Пример:
Введите натуральное число:
4
Количество разложений: 4.

54. Стек

54
Стек
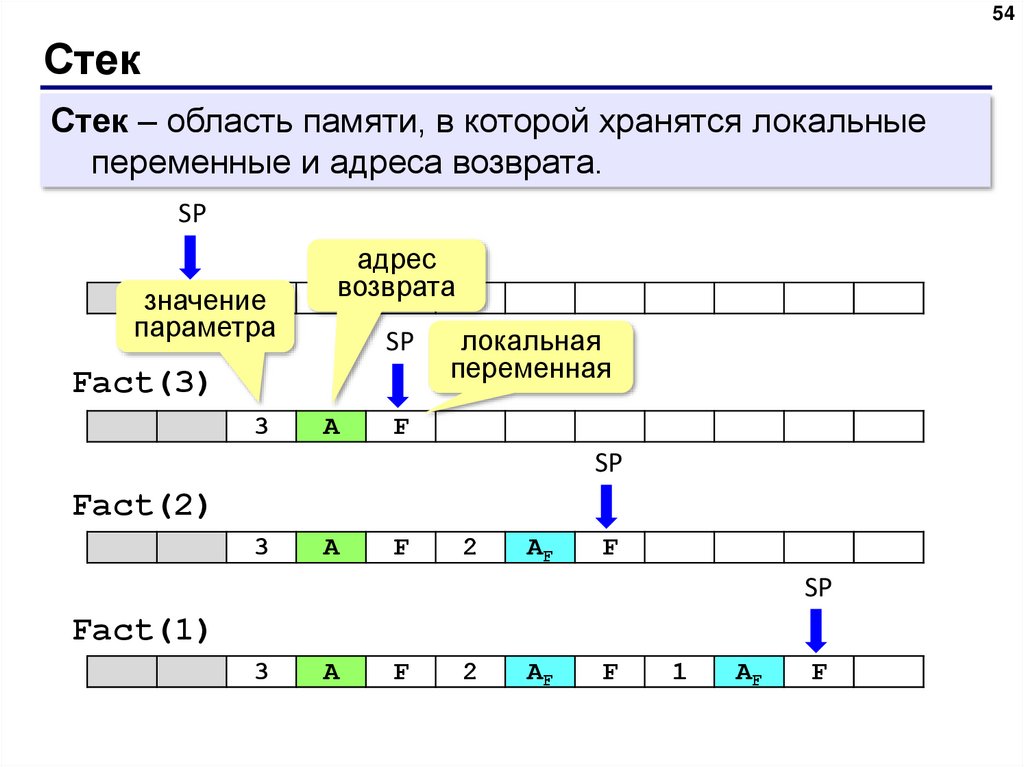
Стек – область памяти, в которой хранятся локальные
переменные и адреса возврата.
SP
значение
параметра
адрес
возврата
SP
Fact(3)
3
A
локальная
переменная
F
SP
Fact(2)
3
A
F
2
AF
F
SP
Fact(1)
3
A
F
2
AF
F
1
AF
F

55. Рекурсия – «за» и «против»

55
Рекурсия – «за» и «против»
• с каждым новым вызовом расходуется память в стеке
(возможно переполнение стека)
• затраты на выполнение служебных операций при
рекурсивном вызове
программа становится более короткой и понятной
возможно переполнение стека
замедление работы
! Любой рекурсивный алгоритм можно заменить
нерекурсивным!
def Fact ( n ):
f=1
for i in range(2,n+1):
итерационный
f *= i
алгоритм
return f