Логические основы устройства компьютера

1. Логические основы устройства компьютера

2. Вентили

Аппаратура современных ЭВМ состоит из некоторых элементарных
конструктивных элементов, называемых вентилями. Каждый
вентиль реализует одну из логических операций, у него есть один
или два входа и один выход. На входах и выходе могут быть
электрические сигналы двух видов:
низкое напряжение, обычно сигнал от 0 до 1В (трактуется как нуль
или логическое значение false);
высокое напряжение, обычно сигнал от 2 до 5В (в Pentium 3,3В)
(ему соответствует единица или логическое значение true).
Вентили могут вычислять различные функции от этих двузначных
сигналов.
Каждый вентиль срабатывает (т.е. преобразует входные сигналы в
выходные) не непрерывно, а только тогда, когда на вентиль по
специальному управляющему проводу приходит так называемый
тактовый импульс. По этому принципу работают ЭВМ, которые
называются дискретными, в отличие от аналоговых компьютеров,
схемы в которых работают непрерывно. Подавляющее число
современных ЭВМ являются дискретными
Ковина Т.П., г.Пермь
2

3. Принципы работы вентилей.

Вся современная цифровая логика основывается на том, что транзистор может
работать как очень быстрый бинарный переключатель.
Каждый логический элемент – это электронно-техническое изделие. В этих
схемах все транзисторы работают в ключевом режиме. Это означает, что при
подаче сигнала высокого уровня на базу транзистора, его сопротивление
становится пренебрежимо малым, то есть транзистор как бы "стягивается в
точку". При низком потенциале на базе транзистора сопротивление между
коллектором и эмиттером становится чрезвычайно большим, что фактически
означает разрыв цепи.
Ковина Т.П., г.Пермь
3

4.

Рассмотрим это на примере работы инвертора. Если сигнал X
имеет высокий потенциал, то ключ, реализованный на
транзисторе, замкнут, и потенциал точки Y низкий. В противном
случае связь между точкой Y и "землей" разорвана, и сигнал Y
имеет высокий уровень, что и обеспечивает реализацию
логической функции "отрицание".
Для элемента "И-НЕ" сигнал в точке Y будет иметь низкий
уровень (НУ) лишь тогда, когда оба сигнала X1 и X2 имеют
высокий уровень (ВУ)
Для элемента "ИЛИ-НЕ" сигнал в точке Y будет иметь высокий
уровень лишь тогда, когда оба сигнала X1 и X2 имеют низкий
уровень.
Ковина Т.П., г.Пермь
4

5. Основные вентили :

Отрицание, этот вентиль имеет один вход и один выход, если на
входе значение true, то на выходе значение false и наоборот.
not
Конъюнкция или логическое умножение, имеет два входа и один
выход, на выходе принимает значение true, если оба значения на
входе true, иначе принимает значение false
and
Дизъюнкция или логическое сложение, на выходе принимает
значение true, если хотя бы одно значение на входе было true,
реализует хорошо известную операцию Паскаля or
or
Ковина Т.П., г.Пермь
5

6. Отрицание

Отрицание реализует операцию « не »
not
1
0
Ковина Т.П., г.Пермь
not
0
1
6

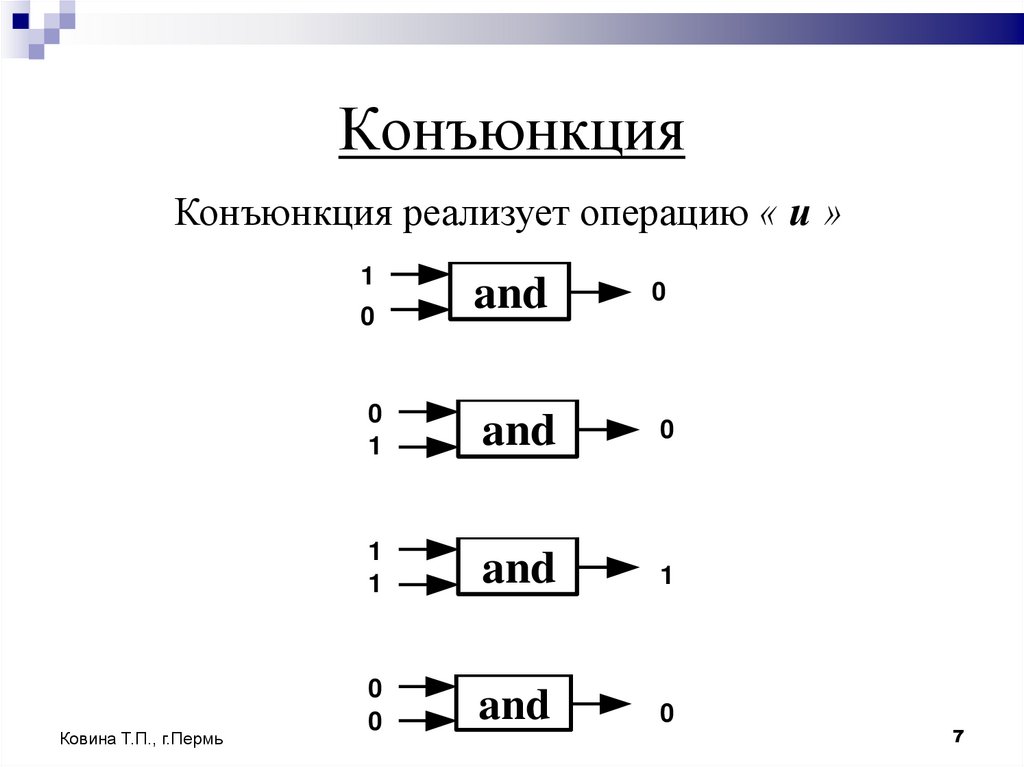
7. Конъюнкция

Конъюнкция реализует операцию « и »
1
Ковина Т.П., г.Пермь
0
0
and
0
1
and
0
1
1
and
1
0
0
and
0
7

8. Дизъюнкция

Дизъюнкция реализует операцию « или »
1
or
1
1
or
1
1
1
or
1
0
0
or
0
0
0
Ковина Т.П., г.Пермь
8

9. Булева алгебра

Чтобы описать схемы, которые строятся путем сочетания различных
вентилей, нужен особый тип алгебры, в которой все переменные и
функции могут принимать только два значения: 0 и 1. Такая алгебра
называется булевой алгеброй. Она названа в честь английского
математика Джорджа Буля (1815-1864).
Как и в обычной алгебре, в булевой алгебре есть свои функции.
Логической (булевой) функцией называют функцию F(Х1, Х2, ..., Хn),
аргументы которой Х1, Х2, ..., Хn (независимые переменные) и сама
функция (зависимая переменная) принимают значения 0 или 1.
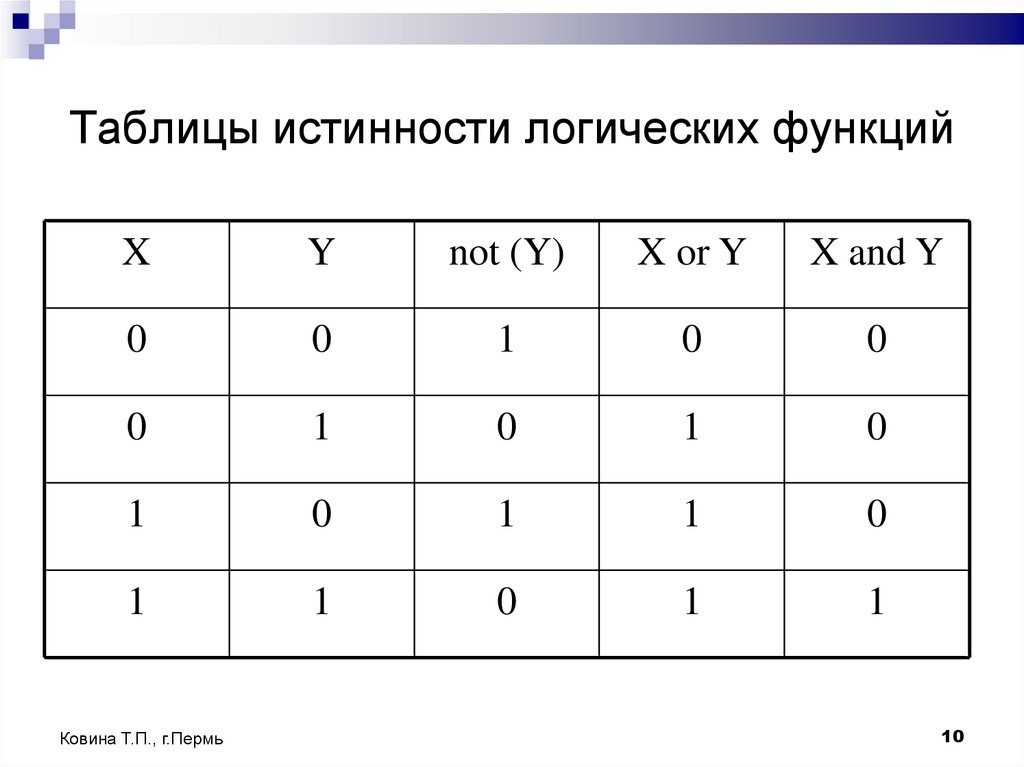
Таблицу, показывающую, какие значения принимает логическая функция
при всех сочетаниях значений ее аргументов, называют таблицей
истинности логической функции. Таблица истинности логической
функции n аргументов содержит 2n строк, n столбцов значений
аргументов и 1 столбец значений функции.
Логические функции могут быть заданы табличным способом или
аналитически — в виде соответствующих формул.
Если логическая функция представлена с помощью дизъюнкций,
конъюнкций и инверсий, то такая форма представления называется
нормальной.
Ковина Т.П., г.Пермь
9

10. Таблицы истинности логических функций

X
Y
not (Y)
X or Y
X and Y
0
0
1
0
0
0
1
0
1
0
1
0
1
1
0
1
1
0
1
1
Ковина Т.П., г.Пермь
10

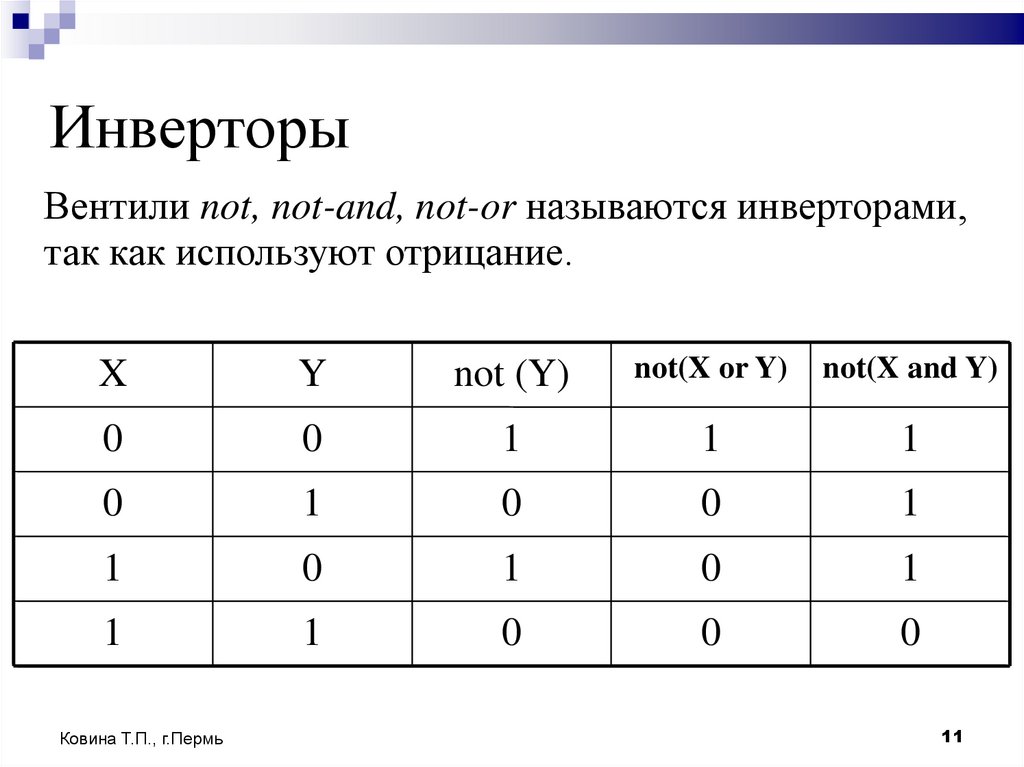
11. Инверторы

Вентили not, not-and, not-or называются инверторами,
так как используют отрицание.
X
Y
not (Y)
not(X or Y)
not(X and Y)
0
0
1
1
1
0
1
0
0
1
1
0
1
0
1
1
1
0
0
0
Ковина Т.П., г.Пермь
11

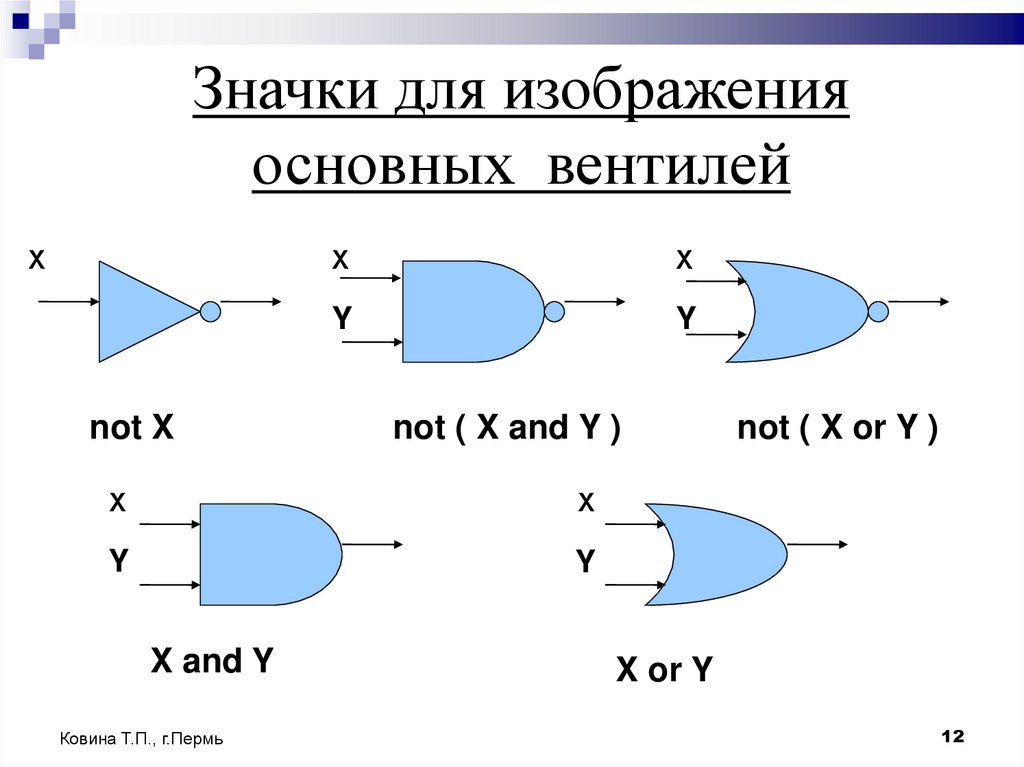
12.

Значки для изображения
основных вентилей
Х
not X
Х
Х
Y
Y
not ( X and Y )
Х
Х
Y
Y
X and Y
Ковина Т.П., г.Пермь
not ( X or Y )
X or Y
12

13. Приоритеты выполнения логических операций:

Операции в скобках
Логическое отрицание not (не)
Конъюнкция (логическое умножение) and (и)
Дизъюнкция (логическое сложение) or (или)
Ковина Т.П., г.Пермь
13

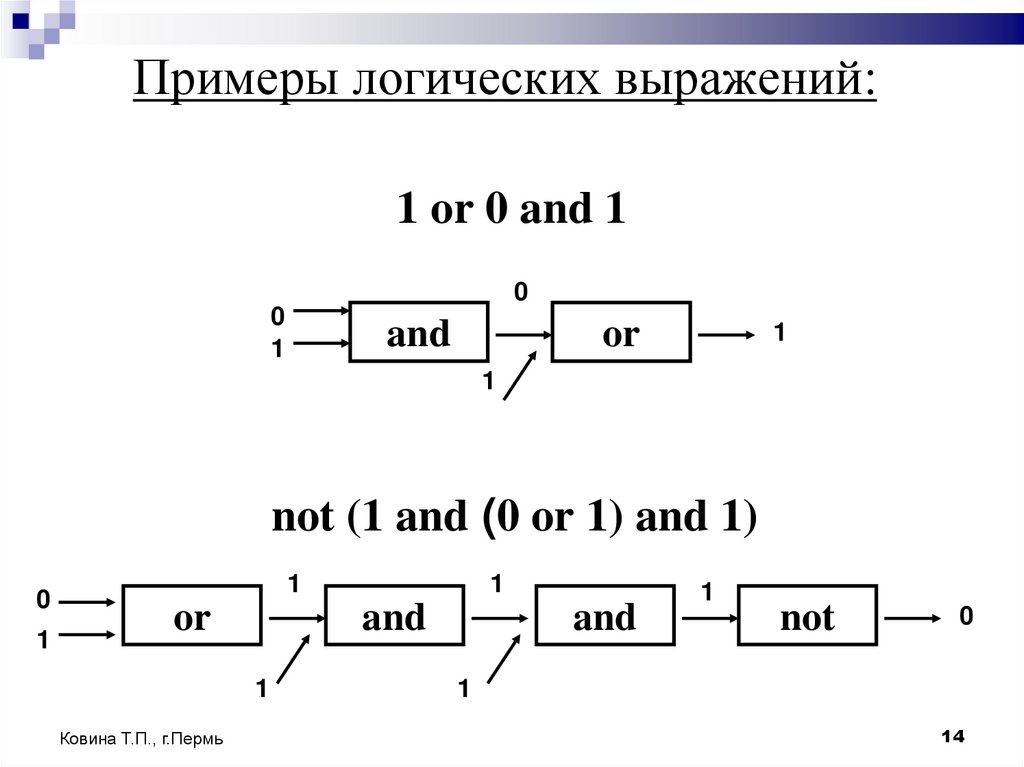
14. Примеры логических выражений:

1 or 0 and 1
0
0
1
and
or
1
1
not (1 and (0 or 1) and 1)
0
1
1
or
and
1
Ковина Т.П., г.Пермь
1
and
1
not
0
1
14

15. Интегральные схемы

Из вентилей строятся так называемые интегральные схемы –
это набор вентилей, соединённых проводами и такими
радиотехническими
элементами,
как
сопротивления,
конденсаторы и индуктивности. Каждая интегральная схема
тоже имеет свои входы и выходы и реализует какую-нибудь
функцию узла компьютера. В специальной литературе
интегральные схемы, которые содержат порядка 1000
вентилей, называются малыми интегральными схемами
(МИС), порядка 10000 вентилей – средними (СИС), порядка
100000 – большими (БИС) и более 100000 вентилей –
сверхбольшими интегральными схемами (СБИС).
Большинство современных интегральных схем собираются на
одной небольшой прямоугольной пластинке полупроводника
с размерами порядка сантиметра. Под микроскопом такая
пластинка СБИС похожа на план большого города.
Интегральная схема имеет от нескольких десятков до
нескольких сотен внешних контактов.
Для того, чтобы реализовать простые электронные часы, необходимо порядка 1000
вентилей, из 10000 вентилей уже можно собрать простейший центральный
процессор, а современные мощные ЭВМ состоят из миллионов вентилей.
Ковина Т.П., г.Пермь
15

16. Полусумматор двоичных чисел.

Рассмотрим
интегральную
схему,
которая
реализует функцию сложение двух одноразрядных
двоичных чисел. Входными данными этой схемы
являются значения переменных x и y, а результатом –
их сумма, которая, в общем случае, является
двухразрядным числом (обозначим разряды этого
числа как P - перенос и S - сумма), формирующиеся
как результат сложения X+Y. Запишем таблицу
истинности для этой функции от двух переменных:
Ковина Т.П., г.Пермь
16

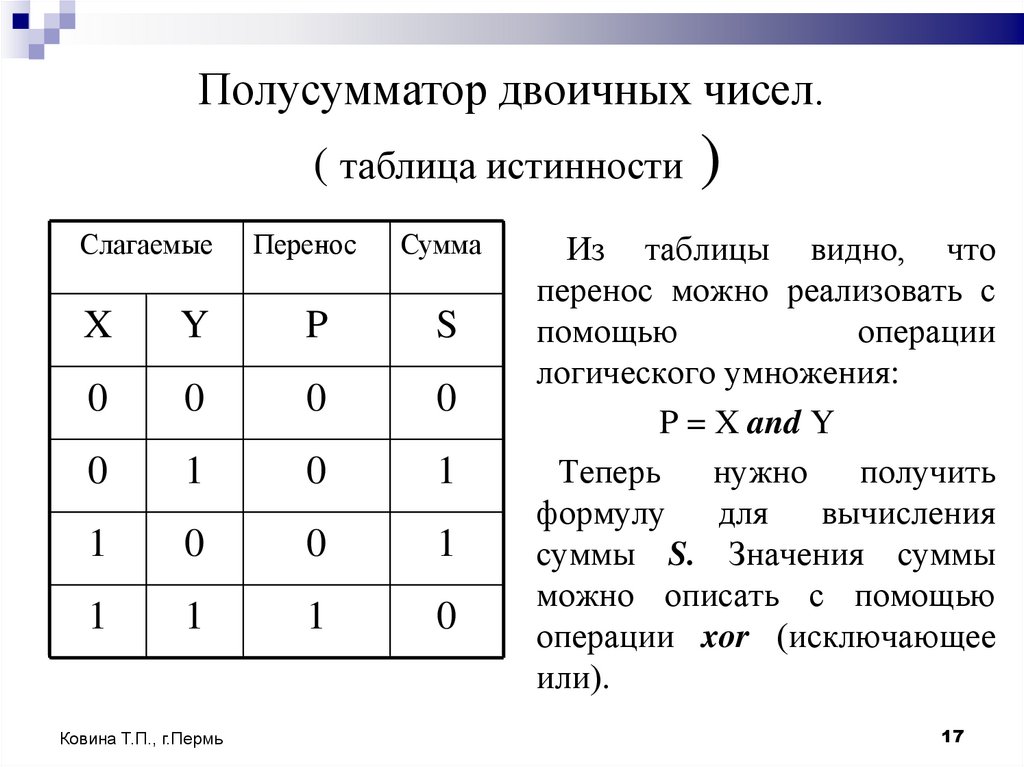
17. Полусумматор двоичных чисел. ( таблица истинности )

Слагаемые
Перенос
Сумма
X
Y
P
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
Ковина Т.П., г.Пермь
Из таблицы видно, что
перенос можно реализовать с
помощью
операции
логического умножения:
P = X and Y
Теперь
нужно
получить
формулу
для
вычисления
суммы S. Значения суммы
можно описать с помощью
операции xor (исключающее
или).
17

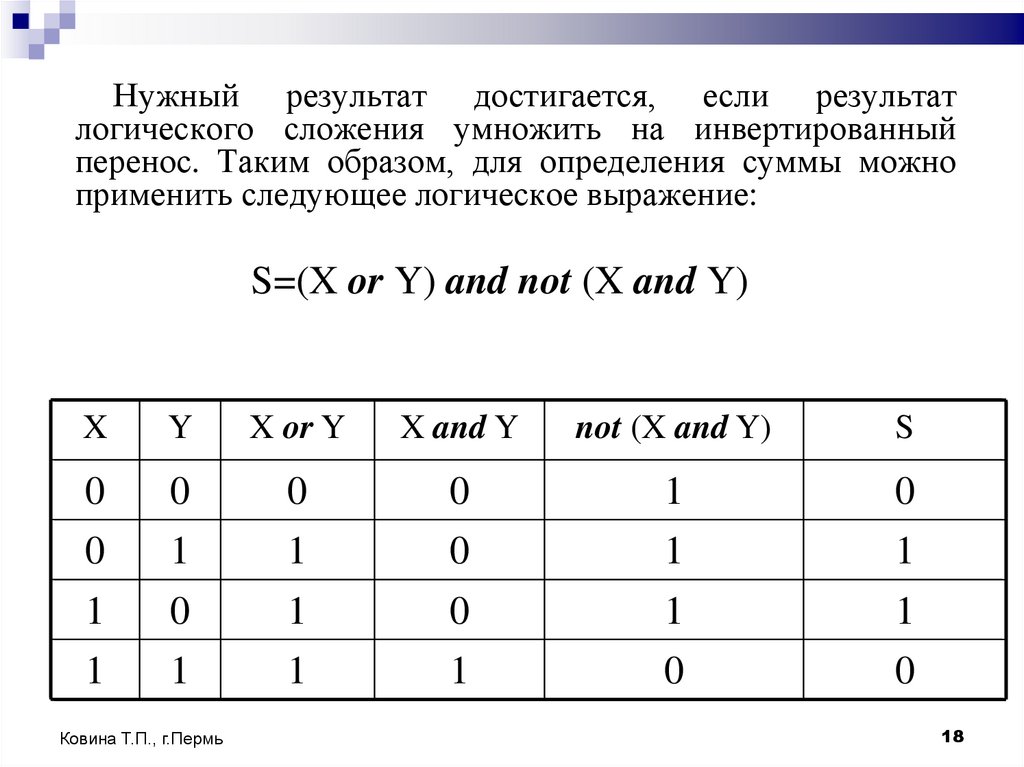
18.

Нужный результат достигается, если результат
логического сложения умножить на инвертированный
перенос. Таким образом, для определения суммы можно
применить следующее логическое выражение:
S=(X or Y) and not (X and Y)
X
Y
X or Y
X and Y
not (X and Y)
S
0
0
0
1
0
1
0
0
1
1
0
1
1
1
0
1
1
1
0
1
1
0
1
0
Ковина Т.П., г.Пермь
18

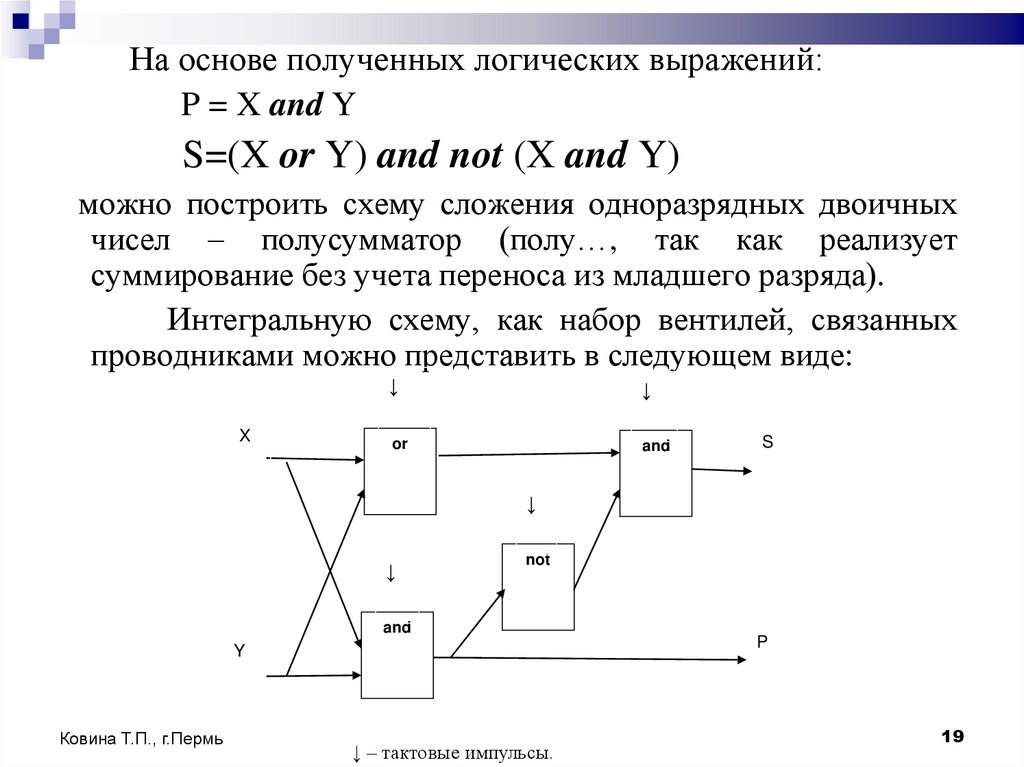
19.

На основе полученных логических выражений:
P = X and Y
S=(X or Y) and not (X and Y)
можно построить схему сложения одноразрядных двоичных
чисел – полусумматор (полу…, так как реализует
суммирование без учета переноса из младшего разряда).
Интегральную схему, как набор вентилей, связанных
проводниками можно представить в следующем виде:
X
↓
↓
or
and
S
↓
↓
not
and
Y
Ковина Т.П., г.Пермь
↓ – тактовые импульсы.
P
19

20. Интегральная схема двоичного сумматора

будет иметь не менее 7-ми внешних контактов: входные X и Y,
выходные P и S, один контакт для подачи тактовых импульсов, два
контакта для подачи электрического питания (ясно, что без энергии
ничего работать не будет) и, возможно, другие контакты.
Суммирование чисел X и Y в приведенной выше схеме осуществляется
после прихода трёх тактовых импульсов (как говорят, за три такта).
Современные компьютеры обычно реализуют более сложные схемы
суммирования, срабатывающие за один такт.
Скорость работы интегральной схемы зависит от частоты прихода
тактовых импульсов, называемой тактовой частотой. У современных
ЭВМ тактовые импульсы приходят на схемы основной памяти с
частотой примерно в сто миллионов раз в секунду, а на схемы
центрального процессора – ещё примерно в 10 раз чаще.
+
X
Y
Ковина Т.П., г.Пермь
–
такт
Интегральная
схема двоичного
сумматора
P
S
Интегральная схема двоичного сумматора.
20

21. Полный одноразрядный сумматор

должен иметь
три входа: X, Y – слагаемые и P0 – перенос
из младшего разряда;
два выхода: сумму S и перенос P;
контакт для подачи тактовых импульсов;
два контакта для подачи электрического
питания.
Ковина Т.П., г.Пермь
21

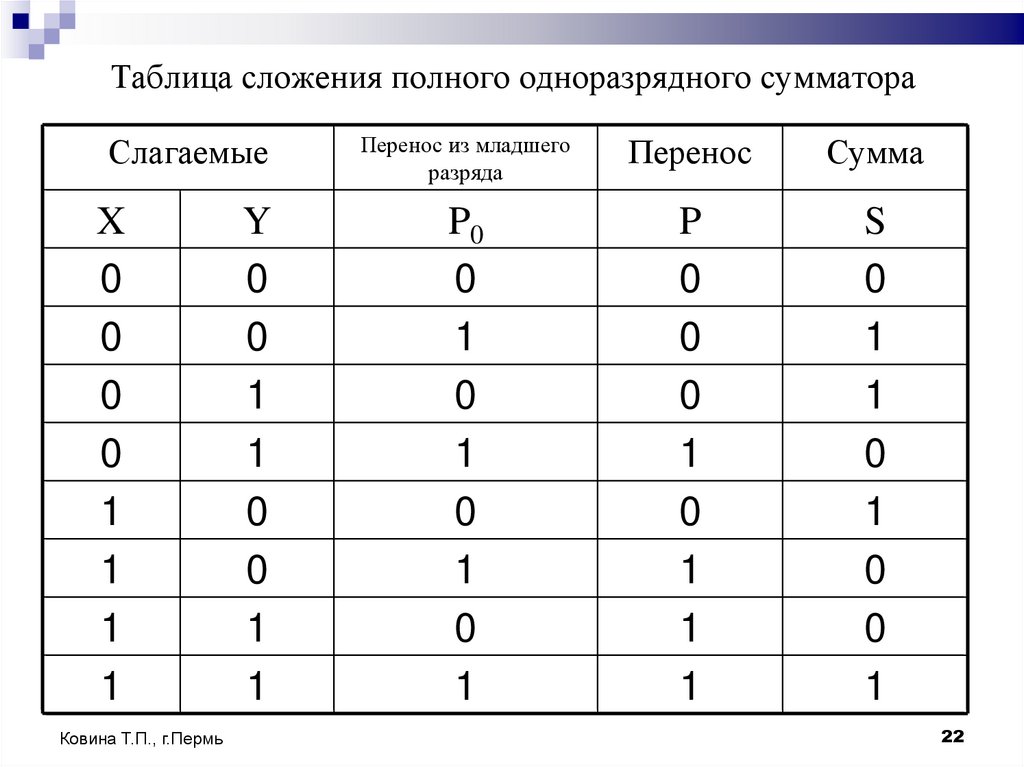
22. Таблица сложения полного одноразрядного сумматора

Слагаемые
X
0
0
0
0
1
1
1
1
Ковина Т.П., г.Пермь
Y
0
0
1
1
0
0
1
1
Перенос из младшего
разряда
Перенос
Сумма
P0
0
1
0
1
0
1
0
1
P
0
0
0
1
0
1
1
1
S
0
1
1
0
1
0
0
1
22

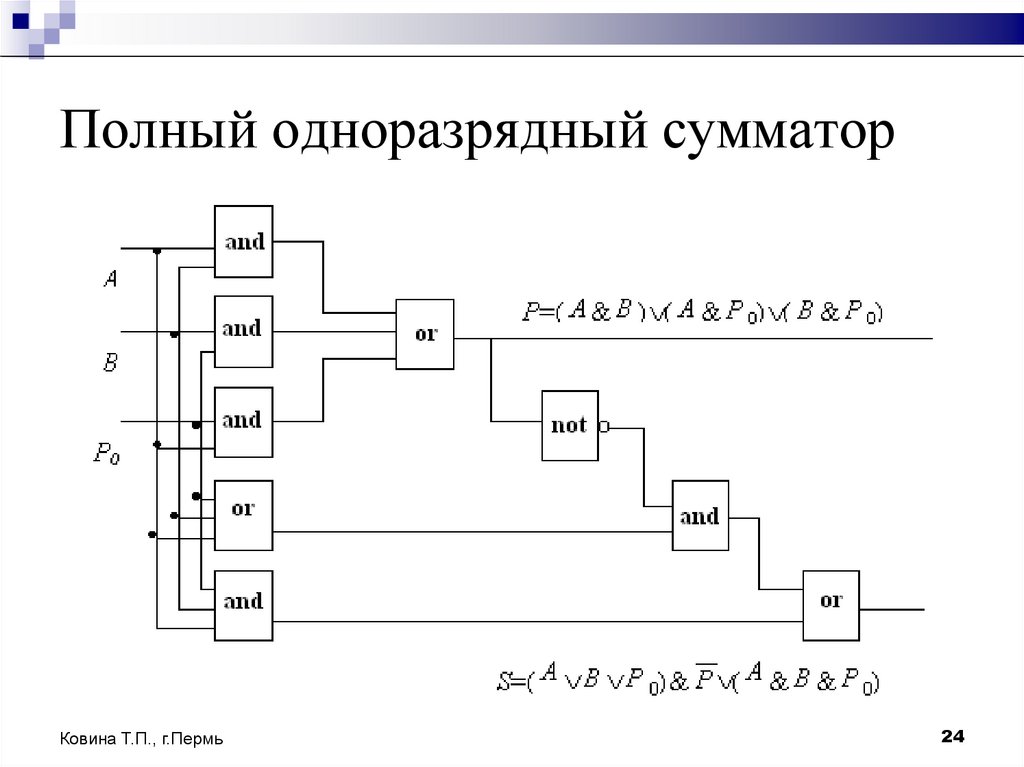
23. Полный одноразрядный сумматор

можно реализовать с помощью следующих
логических выражений:
P=(X and Y) or (X and P0 ) or (Y and P0 )
S=(X or Y or P0 ) and not P or (X and Y and P0 )
Ковина Т.П., г.Пермь
23

24. Полный одноразрядный сумматор

Ковина Т.П., г.Пермь
24

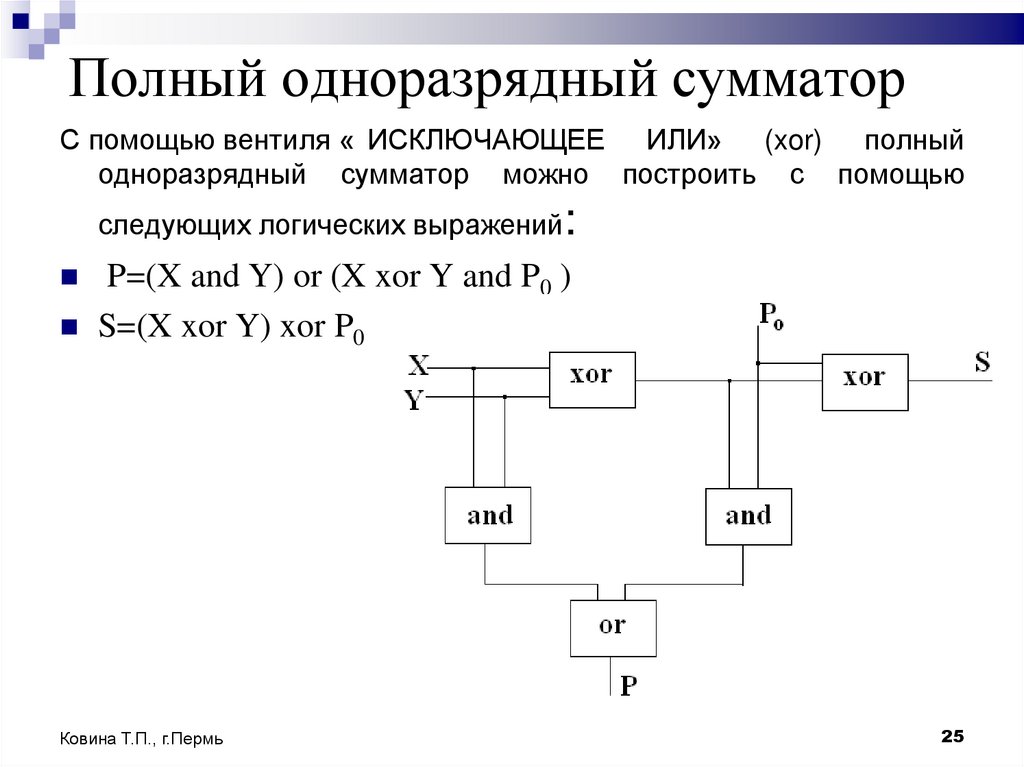
25. Полный одноразрядный сумматор

С помощью вентиля « ИСКЛЮЧАЮЩЕЕ ИЛИ» (xor) полный
одноразрядный сумматор можно построить с помощью
:
следующих логических выражений
P=(X and Y) or (X xor Y and P0 )
S=(X xor Y) xor P0
Ковина Т.П., г.Пермь
25

26. Многоразрядный сумматор

процессора
состоит
из
нескольких
одноразрядых сумматоров. На каждый
разряд ставится одноразрядный сумматор,
причем
выход
(перенос)
сумматора
младшего разряда подключается ко входу
сумматора старшего разряда.
Ковина Т.П., г.Пермь
26

27.

Таким образом, для сложения двух многоразрядных двоичных
чисел на каждый разряд необходим один полный сумматор.
Только в младшем разряде можно обойтись полусумматором.
На рисунке приведена схема, предназначенная для сложения
двух четырехразрядных чисел А и В. Эта схема выпускается в
интегральном исполнении. В ее младшем разряде также
используется полный сумматор, чтобы иметь возможность
наращивания разрядности схемы.
Многоразрядный сумматор с последовательным переносом:

28. Триггер

Важнейшей структурной единицей
оперативной памяти компьютера, а также
внутренних регистров процессора является
триггер.
Это
устройство
позволяет
запоминать,
хранить
и
считывать
информацию (каждый триггер может
хранить 1 бит информации).
Ковина Т.П., г.Пермь
28

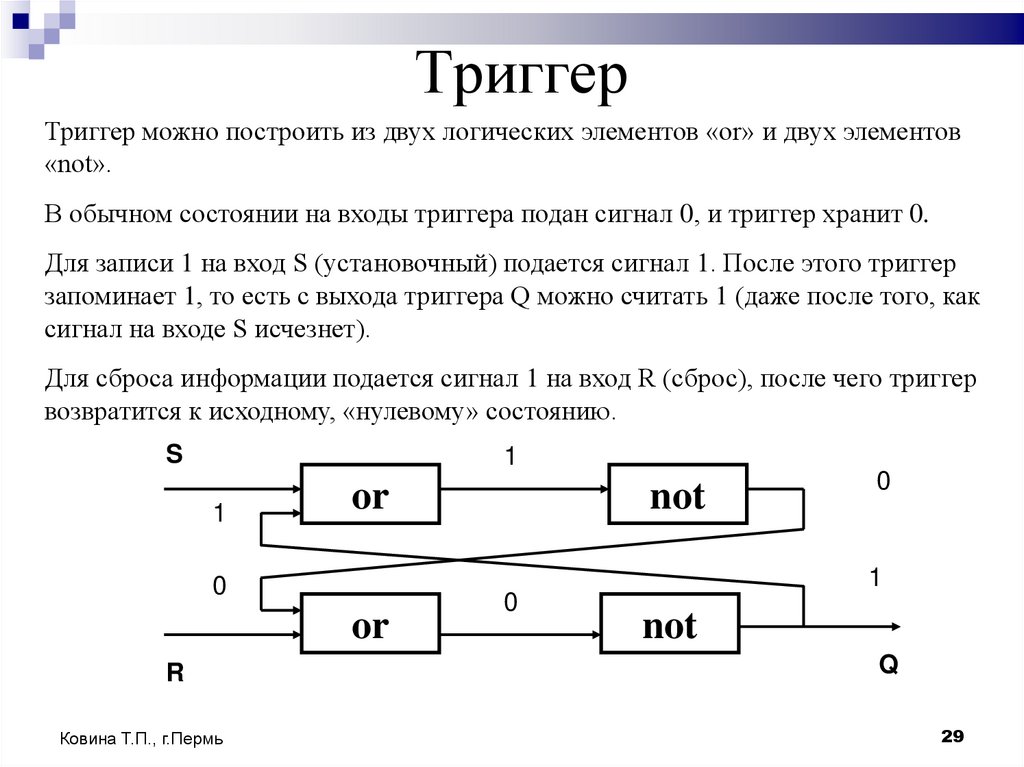
29. Триггер

Триггер можно построить из двух логических элементов «or» и двух элементов
«not».
В обычном состоянии на входы триггера подан сигнал 0, и триггер хранит 0.
Для записи 1 на вход S (установочный) подается сигнал 1. После этого триггер
запоминает 1, то есть с выхода триггера Q можно считать 1 (даже после того, как
сигнал на входе S исчезнет).
Для сброса информации подается сигнал 1 на вход R (сброс), после чего триггер
возвратится к исходному, «нулевому» состоянию.
S
1
1
or
1
0
or
R
Ковина Т.П., г.Пермь
not
0
0
not
Q
29

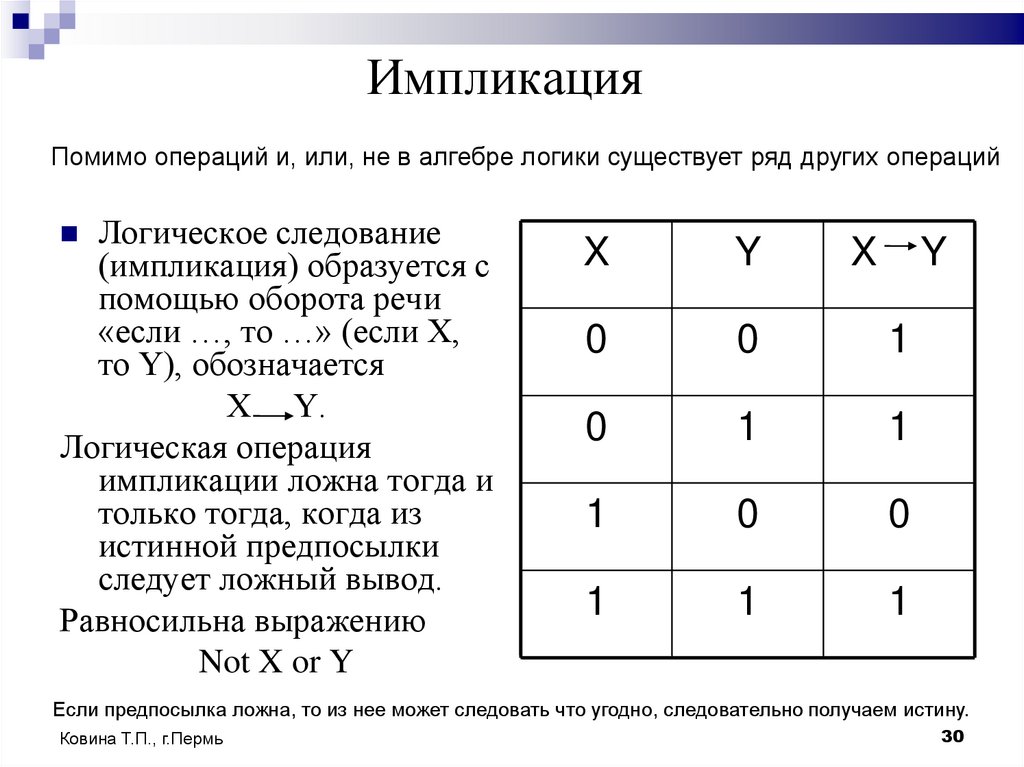
30. Импликация

Помимо операций и, или, не в алгебре логики существует ряд других операций
Логическое следование
(импликация) образуется с
помощью оборота речи
«если …, то …» (если Х,
то Y), обозначается
Х Y.
Логическая операция
импликации ложна тогда и
только тогда, когда из
истинной предпосылки
следует ложный вывод.
Равносильна выражению
Not X or Y
X
Y
X
Y
0
0
1
0
1
1
1
0
0
1
1
1
Если предпосылка ложна, то из нее может следовать что угодно, следовательно получаем истину.
Ковина Т.П., г.Пермь
30

31. Эквивалентность

Логическое равенство
(эквивалентность) образуется
соединением двух высказываний в
одно с помощью оборота речи
«…тогда и только тогда, когда…» (Х
тогда и только тогда, когда Y),
обозначается
Х ~ Y.
Логическая операция эквивалентности
дает истину тогда и только тогда,
когда оба высказывания
одновременно либо ложны, либо
истинны.
Равносильна логическому выражению
(X or not Y) and (not X or Y)
Ковина Т.П., г.Пермь
X
Y
X~Y
0
0
1
0
1
0
1
0
0
1
1
1
31

32. Логические законы и правила преобразования логических выражений

Логические выражения называются
равносильными, если их таблицы истины
совпадают при любых значениях, входящих в них
логических переменных.
Равносильные преобразования логических
формул служат для упрощения формул или
приведения их к определенному виду путем
использования основных законов алгебры логики.
Ковина Т.П., г.Пермь
32

33. Законы алгебры логики

Закон тождества: Всякое высказывание тождественно самому
А=A
Закон двойного отрицания: Если дважды отрицать
себе
некоторое высказывание, то в результате мы получим исходное
высказывание.
А=
Закон непротиворечия
А & ( ) =0
Невозможно, чтобы противоречащие высказывания были одновременно
истинными.
Законы исключения третьего:
А ( ) =1
Из двух противоречащих высказываний об одном и том же предмете одно
всегда истинно, а второе — ложно, третьего не дано.
Ковина Т.П., г.Пермь
33

34. Законы алгебры логики

Законы исключения констант:
— для логического сложения:
A 1 = 1, A 0 = A;
— для логического умножения:
A&1 = A, A&0 = 0.
Закон идемпотентности ( от латинских слов idem — тот же
самый и potens —сильный; дословно — равносильный):
— для логического сложения:
A A = A;
— для логического умножения:
A&A = A.
Закон означает отсутствие показателей степени.
Ковина Т.П., г.Пермь
34

35. Законы алгебры логики

Закон общей инверсии (законы де Моргана):
— для логического сложения
= &
— для логического умножения:
=
Ковина Т.П., г.Пермь
35

36. Законы алгебры логики

Переместительный (коммутативный)
закон:
— для логического сложения:
А B = B A;
— для логического умножения:
A&B = B&A.
Результат операции над высказываниями не зависит от
того, в каком порядке берутся эти высказывания.
В обычной алгебре
a + b = b + a, a * b = b * a.
Ковина Т.П., г.Пермь
36

37. Законы алгебры логики

Сочетательный (ассоциативный) закон:
— для логического сложения:
(A B) C = A (B C);
— для логического умножения:
(A&B)&C = A&(B&C).
При одинаковых знаках скобки можно ставить произвольно или
вообще опускать.
В обычной алгебре:
(a + b) + c = a + (b + c) = a + b + c,
Ковина Т.П., г.Пермь
37

38. Законы алгебры логики

Распределительный (дистрибутивный) закон:
— для логического сложения:
(A B)&C = (A&C) (B&C);
— для логического умножения:
(A&B) C = (A C)&(B C).
Определяет правило выноса общего высказывания за
скобку.
В обычной алгебре:
(a + b) * c = a * c + b * c.
Ковина Т.П., г.Пермь
38

39. Законы алгебры логики

Закон поглощения:
— для логического сложения:
A (A&B) = A;
— для логического умножения:
A & (A B) = A.
Закон исключения (склеивания):
— для логического сложения:
(A&B) ( &B) = B;
— для логического умножения:
(A B) & (
B) = B.
Ковина Т.П., г.Пермь
39