Комплексные числа История появления и роль в нашей жизни. Примеры нахождения комплексных корней

1.

Комплексные
числа
История появления и роль в нашей
жизни.
Примеры нахождения комплексных
корней.

2.

Комплексные
числа: Введение
• Что такое комплексные числа? (a
+ bi) где i - мнимая единица)
• Необходимость введения
комплексных чисел для решения
уравнений
• Краткий обзор истории и области

3.

Транзистор
В электротехнике комплексные числа
используются для анализа цепей
переменного тока. Концепция
импеданса, которая описывает
сопротивление цепи переменного тока,
является комплексной величиной.
Импеданс — комплексная величина
электрической цепи, выраженная
действительным сопротивлением и мнимым
реактивным сопротивлением, препятствующая
прохождению электрического тока.

4.

XVI век и кубические
уравнения
XVI век ознаменовался
значительным прогрессом в
алгебре. Математики того времени
бились над решением кубических
уравнений – уравнений вида ax³ +
bx² + cx + d = 0.
Но все же, один математик того
времени знал как решать такие
уравнения.

5.

Дуэли математиков
Тарталья против Фиоре
В 16• веке
математики придумали для себя забаву. Они стали
афывафыв
вызывать друг друга на публичную дуэль. Математическая
дуэль представляла собой решение задач на время. Эти дуэли
были важны для них, так как победители получали славу и
хорошую работу в университетах, а проигравшие - публичный
позор.
В 1534 году происходит самая интересная математическая
дуэль, которая повлияет на историю человечества.
Некий Антонио Фиоре вызывает на дуэль Никколо Тарталья

6.

Дуэли математиков
Тарталья против Фиоре
• Антонио Фиоре умел решать кубические уравнения. Но только
неполные. (Уравнения вида: ax³ + bx + c = 0)
Эта способность досталась ему от его учителя математики
Сципио́
на дель Фе́
рро.
Спустя 8 лет после получения формулы, Фиоре вызывает на
дуэль Тарталья. За полтора месяца нужно решить 30 задач,
которыми они обмениваются друг с другом.
Тарталья отправляет ему список различных задач. А Фиоре
ставит все на свою формулу и составляет 30 неполных
кубических уравнений.
Тарталья в последний день находит собственный способ
решения
кубических уравнений. Он решает все задачи за 2 часа, и
побеждает на дуэли, так как Фиоре не решил ни одной
задачи.

7.

Бомбелли и "Алгебра"
Формула Кардано, выведенная в 1545 году, позволяла
решать кубические уравнения. Однако она сталкивалась с
проблемами в "неразрешимых" случаях, когда требовалось
извлекать корни из отрицательных чисел.
Пример
Бомбелли показал, как использование мнимого числа
√(-121) = 11i упрощает решение кубического уравнения.
В своей "Алгебре" (1572) Бомбелли впервые попытался
формализовать правила оперирования с комплексными
числами, чтобы объяснить парадоксы, возникающие при
решении кубических уравнений.

8.

Дальнейшее развитие:
От Эйлера до Гаусса
XVII-XVIII века
Лейбниц, Бернулли, Эйлер развивали теорию
комплексных чисел. Эйлер ввел обозначение "i"
для √(-1) и формализовал правила работы с ними.
XIX век
Гаусс предложил геометрическую интерпретацию
комплексных чисел, представляя их как точки на
плоскости. Это дало им геометрический смысл и
сделало их использование более понятным и
наглядным.

9.

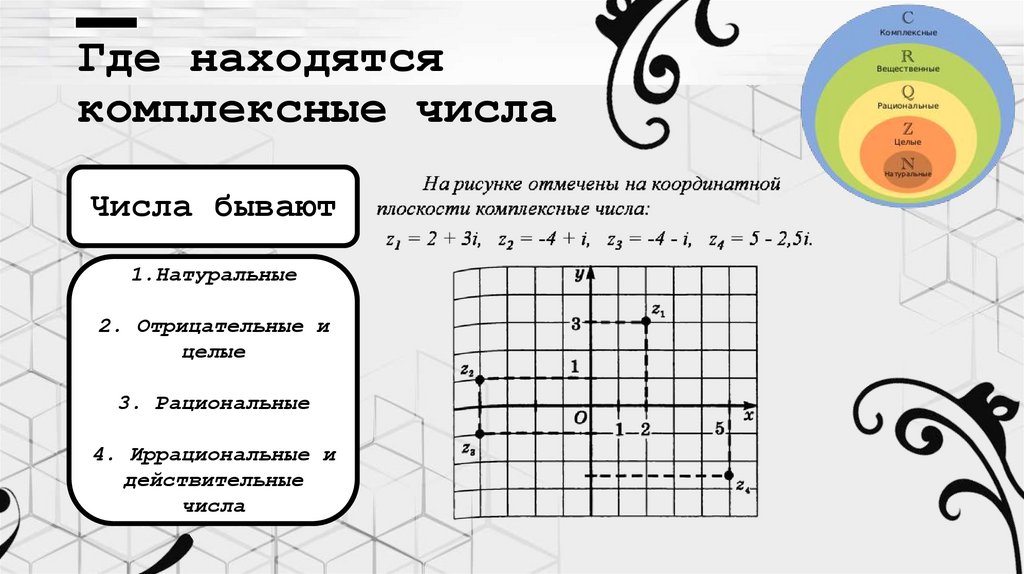
Где находятся
комплексные числа
Числа бывают
1.Натуральные
2. Отрицательные и
целые
3. Рациональные
4. Иррациональные и
действительные
числа

10.

Операции
с комплексными числами
Какие
операции
можно
проводить?
Сложение и вычитание
умножение и деление

11.

Решение примеров
с комплексными числами
Решение:
Мы знаем,
что
Этого нам, собственно
говоря, уже достаточно.
Действительно, тогда
Далее,

12.

Решение уравнений с
комплексными числами
Найти x, y если
Два комплексных числа равны тогда и только
тогда, когда у них равны вещественные и мнимые
части. Таким образом, должны быть выполнено
одновременно:
Находим, что
А, значит,

13.

Современные применения
комплексных чисел
Электротехника
Комплексные числа
используются для
анализа цепей
переменного тока,
моделирования
импеданса, который
является комплексной
величиной.
Комплексные числа
используются для
анализа цепей
переменного
тока, характеризующих
сопротивление
Квантовая
механика
Комплексные числа
используются в
квантовой механике
для описания
волновой функции,
которая
представляет собой
комплексное число,
и для решения
уравнения
Шредингера.
Гидродинамика
Комплексные числа
применяются для
описания потоков
жидкости и газа, а также
для решения задач,
связанных с волнами.

14.

Комплексные числа
как мощный инструмент
Заключение: Комплексные числа как мощный инструмент
Комплексные числа стали неотъемлемой частью
современной науки и техники.
Они используются в электротехнике, гидродинамике,
квантовой механике, теории управления и других
областях. Благодаря формализации и геометрической
интерпретации, они стали удобным инструментом для
решения сложных задач.

15.

Спасибо за
внимание
Сделали ученики Поваровской СОШ
Мотриченко Максим и Робакидзе
Георгий