Похожие презентации:
Программирование циклов. Итерационные процессы. Лекция 5
1.
Лекция 5Программирование циклов.
Итерационные процессы.
2.
Что такое итерационный процесс?• Итерационный процесс - это процесс с применением
повторяющего действия.
• На латыни слово iteratio значит повторяю.
• Если что-то повторяется, то это можно назвать
итерационным процессом.
• Обычно данное понятие используется в математике и
программировании.
• В программировании - это просто употребление циклов
для повторения некоторых участков кода.
• А в математике итерационным процессом называют
повторение какого-либо действия для более точного его
вычисления.
• Итерационный процесс - это процесс последовательных
приближений
3.
Формализация ИППусть имеется начальное состояние процесса Х0 и
некоторая формула F, такая что
Хn = F(Xn-1)
для всех n = 1,2,3,…
Тогда последовательность состояний
X0, X1, X2,…, Xn, Xn+1,…
представляет собой итерационный процесс (ИП).
ИП характеризуется точкой отсчета (начальное
состояние) и закономерностью получения нового
состояния процесса из предыдущего
4.
Примеры вычисления ИПСосчитать сумму y = 1 + 2 + 3 +… + n
Какой здесь ИП?
Состояние процесса - величина у
Найдем закономерность изменения состояния.
Как изменяется у от шага к шагу?
1 шаг у1 = 1
2 шаг у2 = 1 + 2
3 шаг у3 = 1 + 2 + 3
…
(i – 1)-й шаг yi -1 = 1 + 2 + 3 +…+ (i– 1)
i-тый шаг
yi = 1 + 2 + 3 +…+ i = yi -1+ (i)
Итак, у нас есть все данные для ИП. Составим
алгоритм и напишем код.
5.
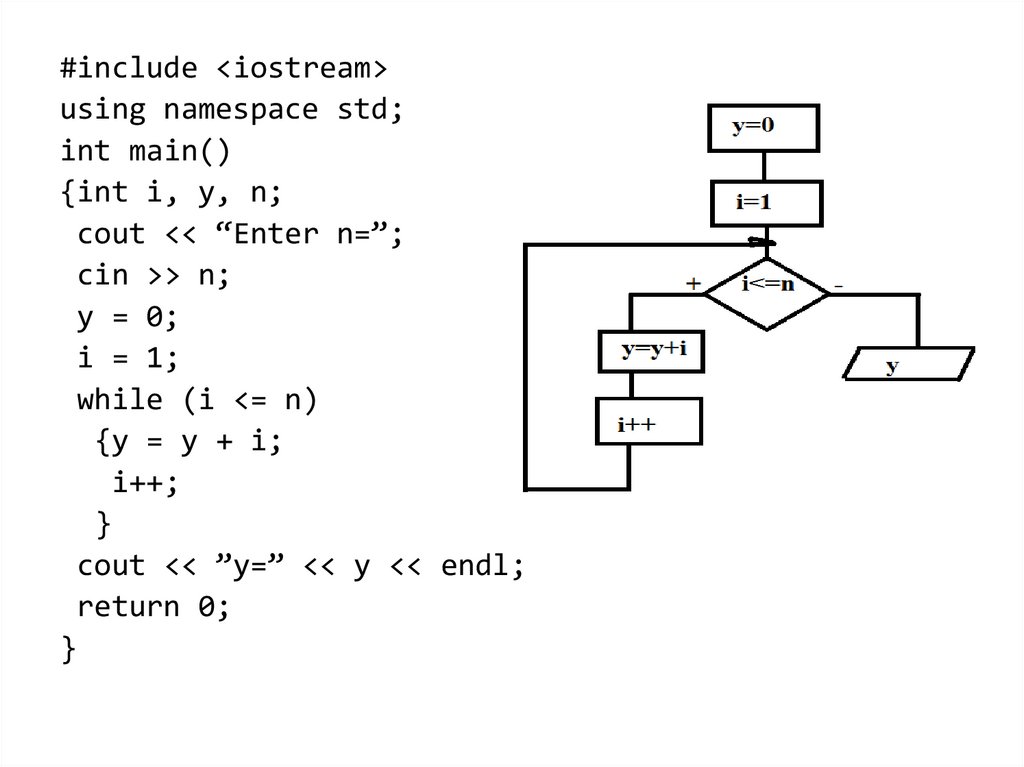
#include <iostream>using namespace std;
int main()
{int i, y, n;
cout << “Enter n=”;
cin >> n;
y = 0;
i = 1;
while (i <= n)
{y = y + i;
i++;
}
cout << ”y=” << y << endl;
return 0;
}
6.
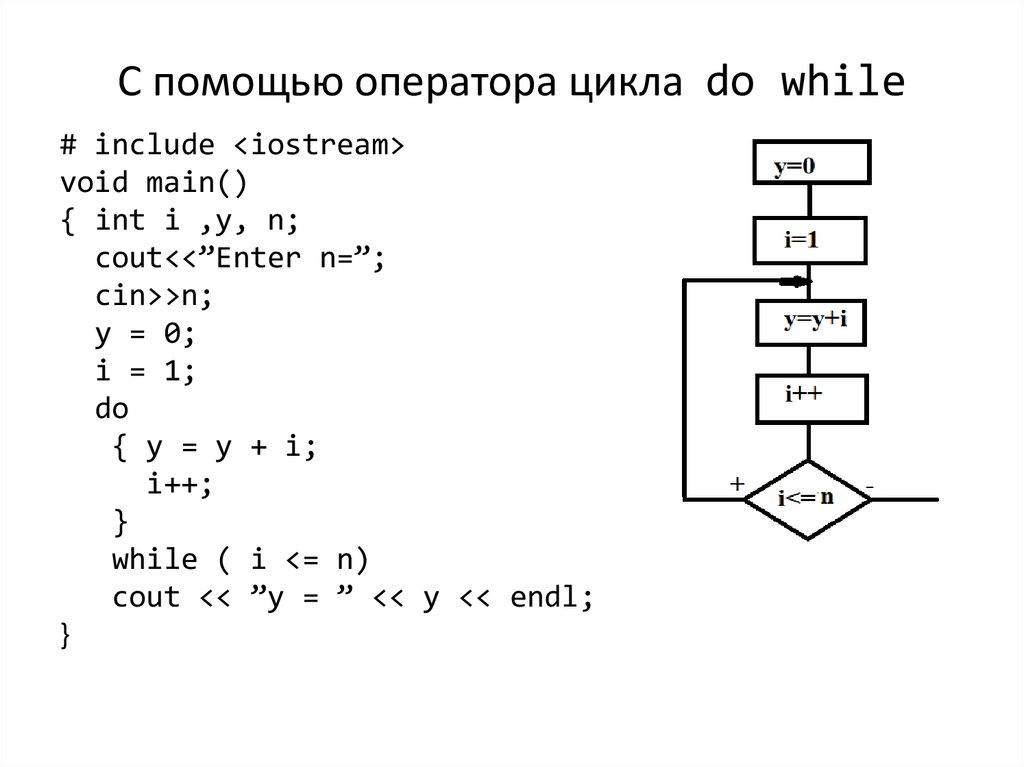
С помощью оператора цикла do while# include <iostream>
void main()
{ int i ,y, n;
cout<<”Enter n=”;
cin>>n;
y = 0;
i = 1;
do
{ y = y + i;
i++;
}
while ( i <= n)
cout << ”y = ” << y << endl;
}
7.
С помощью оператора цикла for#include <iostream>
using namespace std;
int main()
{int i, y, n;
cout << “Enter n=”;
cin >> n;
y = 0;
for (i = 1; i <= n; i++)
y = y + i;
cout << ”y = ” << y << endl;
return 0;
}
8.
Пример: вычисление функции синусаразложением в ряд
sin( x) = ∑0n (-1)i x2i+1 / (2i+1)!
Чтобы понять характер вычислений,
распишем это выражения для разных
значений i:
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =
при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
9.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
y = y + znak * a/b;
10.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
a = a * x* x;
y = y + znak * a/b;
11.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
3*2*1! 5*4*3! 7*6*5!...
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
12.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
13.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1;
14.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
while (i ?){
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1; }
15.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
i=
while (i ?){
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1; }
16.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
y=
i=
while (i ?){
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1; }
17.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
a=
y=
i=
while (i ?){
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1; }
18.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
b=
a=
y=
i=
while (i ?){
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1; }
19.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak =
b=
a=
y=
i=
while (i ?)
{
znak = -znak ;
b = b * (2 * i + 1) * (2* i);
a = a * x* x;
y = y + znak * a/b;
i = i + 1;
}
20.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak =
b=
a=
y=
i=
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
21.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak =
b=
a=
y = x;
i=
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
22.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak =
b=
a = x;
y = x;
i=
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
23.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak =
b = 1;
a = x;
y = x;
i=
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
24.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i=
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
25.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i ?)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
26.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
}
27.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
2
}
28.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
2
}
1
29.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
2
}
1
3!*4*5 = 5!
30.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
a = a * x* x;
x3 = x * x* x
y = y + znak * a/b;
x/1! - x3/3!
i = i + 1;
2
}
1
3!*4*5 = 5!
x3 * x* x = x 5
31.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1;
while (i <= n)
{ znak = -znak ;
-1
1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
3!*4*5 = 5!
a = a * x* x;
x3 = x * x* x
x3 * x* x = x 5
y = y + znak * a/b;
x/1! - x3/3!
x/1! - x3/3! + x 5 /5!
i = i + 1;
2
3
…
}
(см. код)
32.
y = sin( x) = ∑0n (-1)i x2i+1 / (2i+1)! =при i = 0
1
2
3
…
= x/1! - x3/3! + x 5 /5! – x 7/7! +…
cin >> x;
znak = 1;
b = 1;
a = x;
y = x;
i = 1; i= 0;
while (i <= n i <= n – 1 или i < n )
{ i = i + 1;
1
2
znak = -znak ;
-1
1
b = b * (2 * i ) * (2* i + 1);
3! = 1 * 2 * 3
3!*4*5 = 5!
a = a * x* x;
x3 = x * x* x
x3 * x* x = x 5
y = y + a/b;
x/1! - x3/3!
x/1! - x3/3! + x 5 /5!
*! i = i + 1;
2
3
…
}
(см. код)
33.
Универсальный способ.y = ∑0n (-1)i x2i+1 / (2i+1)! = ∑0n ti
ИП : t0 , t1 , t2 , t3 , t4 , ...... , tn.
ti =ti-1*p
p = ti/ ti-1= ((-1)i x2i+1 / (2i+1)!)/
((-1)i-1 x2i-1 / (2i-1)!) =
-x2/2*i*(2*i+1)
(см. код)
34.
Три схемы обрыва ИПНе всегда нам бывает известно то количество шагов,
которое нужно сделать в процессе вычисления.
Задача
Вычислить сумму ряда Грегори
, когда n . Для заданного = 0.0001 найти
наименьшее n такое, что
35.
Первая схема обрыва ИПусловие накладывается на все выражение в целом.
(См. рисунок)
Схема алгоритма:
1. вычисляем первое значение выражения
2. проверяем, достаточно ли мы приблизились к нужному
значению (сравниваем с ε расстояние между
значением выражения и точным значением):
если расстояние еще большое, вычисляем новое
значение выражения и переходим снова к проверке ( к
шагу 2)
если расстояние уже маленькое (<= ε), то мы нашли
нужный шаг, вычислили нужное значение, переходим к
шагу 3
3. процесс завершен.
(См. пример)
36.
ЗадачаВычислить приближенное значение
постоянной Каталана – следующей
знакопеременной суммы:
"обрывая" суммирование как только
очередной член ряда становится по
абсолютной величине .
37.
Вторая схема обрыва ИПусловие накладывается на отдельный элемент ряда.
(См. рисунок)
Схема алгоритма:
1. вычисляем первый элемент ряда
2. проверяем, достаточно ли еще большой этот
вычисленный элемент (сравниваем его с ε) :
если он еще достаточно большой, используем его, а
затем вычисляем новый элемент ряда и переходим
снова к проверке ( к шагу 2)
если элемент уже маленький (<= ε), то (следовательно,
остальные будут еще меньше) переходим к шагу 3
3. процесс завершен.
(См. пример)
38.
ЗадачаПоследовательность {x0, x1,…} определяется
рекуррентно. Найти наименьшее n, при
котором |xn-xn-1| .
k = 1, 2 ,…; x0 = 0
39.
Третья схема обрыва ИПусловие накладывается на расстояние между двумя
последовательными элементами ряда.
(См. рисунок)
Схема алгоритма:
1. вычисляем первые два элемента ряда
2. проверяем расстояние между ними (сравниваем его с ε):
если оно еще достаточно большое, то вычисляем новый
элемент ряда и переходим к проверке расстояния между ним
и предыдущим элементом( к шагу 2)
если оно уже маленькое (<= ε), то (следовательно, остальные
расстояния будут еще меньше) переходим к шагу 3
3. процесс завершен.
(См. пример)
40.
Часто встречающиеся ошибки• Считать факториал и степень в отдельные переменные
• Считать факториал или степень в отдельном цикле внутри
общего цикла
• Использовать для подсчета степени функцию pow(a, b):
мы с каждой итерацией наращиваем степень, а не
вычисляем ее заново!
• Вычислять знак с помощью функции pow(a, b)
• Путать знак неравенства при проверке условия в схемах
обрыва ИП
41.
Типы итерационных процессов• Точечные ИП
• ИП большей глубины
• Параллельные ИП
42.
Точечные ИППример:
x0 = a; xk = bxk–1+c,
k = 1, 2,…;
Точечные ИП характеризуются тем, что для вычисления
всей последовательности значений {x0, x1, …}
достаточно одной переменной, т.е. все значения
проходят только через одну область в памяти.
Фрагмент кода:
double x = a;
for (int i = 1; i <= n; i++)
{
x = b * x + c;
}
43.
ИП большей глубиныПример: x0 =a; x1 = b;
xk=cxk–1+ dxk-2, k = 2, 3, … ; (ИП глубины 2)
Распишем:
x2 = cx1+ dx0
x3= cx2 + dx1,
x4= cx3 + dx2, …
Мы видим, что в вычислении участвует три области
памяти – три переменных. Обозначим их:
xn – «х новое» , хs – «х старое» и xss – «х совсем старое.
Тогда все вычисление сведется к формуле:
xn = c * xs + d * xss;
Но всякий раз содержимое этих переменных меняется,
а именно, «старый» становится «совсем старым», а
«новый» - «старым»
44.
Получим следующий фрагмент кода:double xss = a, xs = b;
for (int i = 2; i <= n; i++)
{
xn = c * xs + d* xss;
xss = xs;
xs = xn;
}
Заметим,
что
«перекидку»
нужно
начинать
со
«старших» значений. Почему? Потому что «самый старый» в
дальнейших вычислениях не участвует, следовательно его
можно «затереть». В него сохраняем «старого». Значит
переменную, отведенную под «старого» можно тоже
затереть. В нее кладем «нового». А теперь мы готовы
получить нового «нового», место вакантно.
Нетрудно видеть, что, если мы имеем ИП глубины k, то
для организации процесса без потери данных нам нужна
k + 1 переменная.
45.
Параллельные ИППример: x0 = y0 = a,
xk = bxk–1+ cyk–1,
yk = dxk–1+ eyk–1, k = 1, 2,…;
Параллельно разворачиваются два
взаимозависимых ИП. В данном примере мы
видим, что на каждом шаге итерации нам
нужны «старые» значения в обоих процессах.
Следовательно, мы должны их сохранять до
окончания вычисления «новых», затем
обновить и передать в следующую итерацию.
Для этого нужны 4 переменные: xs, xn, ys, yn.
46.
Получим следующий фрагмент кода:double xs = ys = a;
for (int i = 1; i <= n; i++)
{
xn = b * xs + c * ys;
yn = d * xs + e * ys;
xs = xn;
xy = yn;
}
Заметим, что иногда в каком-то из параллельных процессов
может развиваться точечный ИП. Это даст некоторую экономию
в переменных. Но нужно быть очень аккуратным при таких
вычислениях. Иногда лучше подстраховаться и использовать
полный набор переменных.






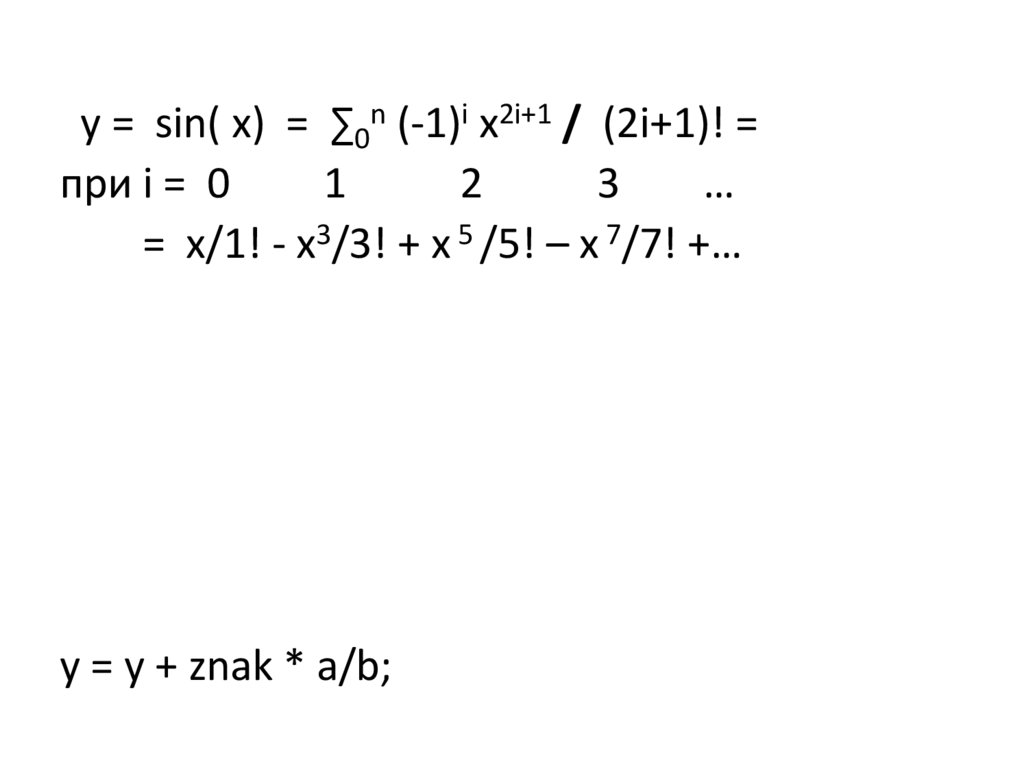
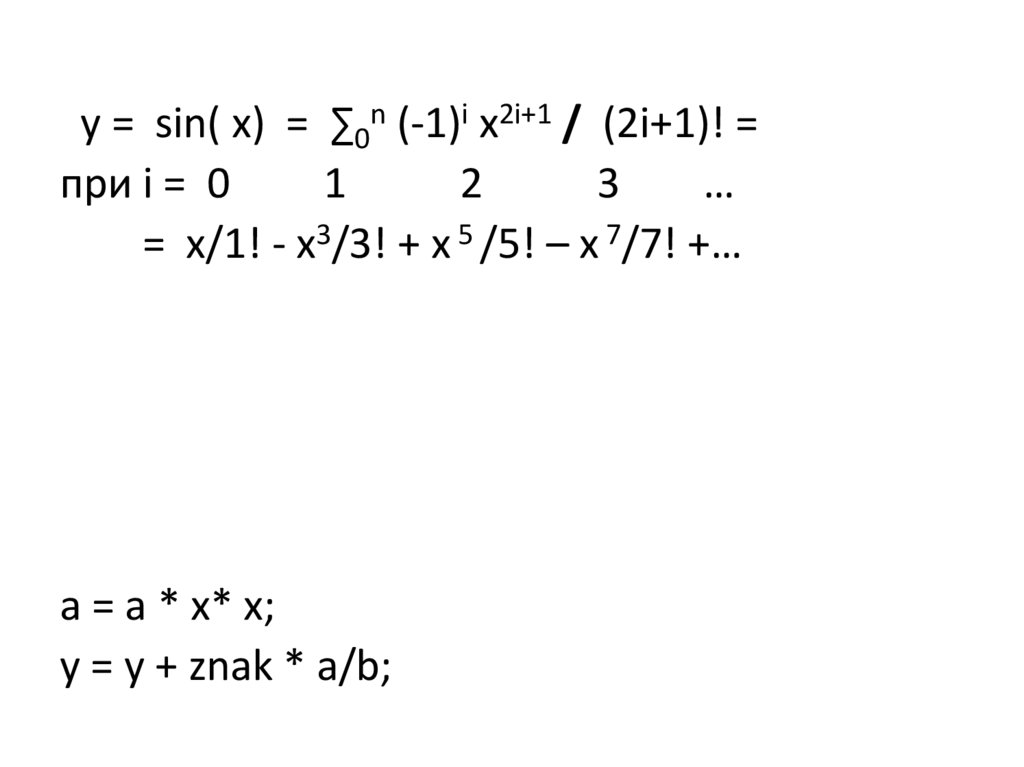
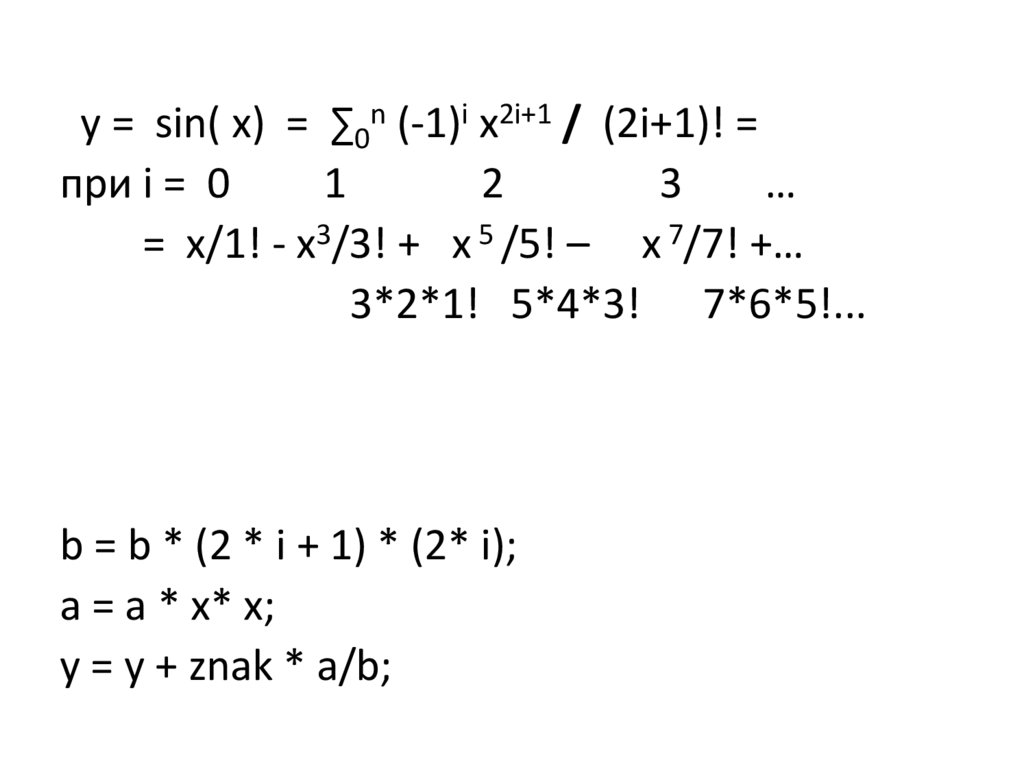
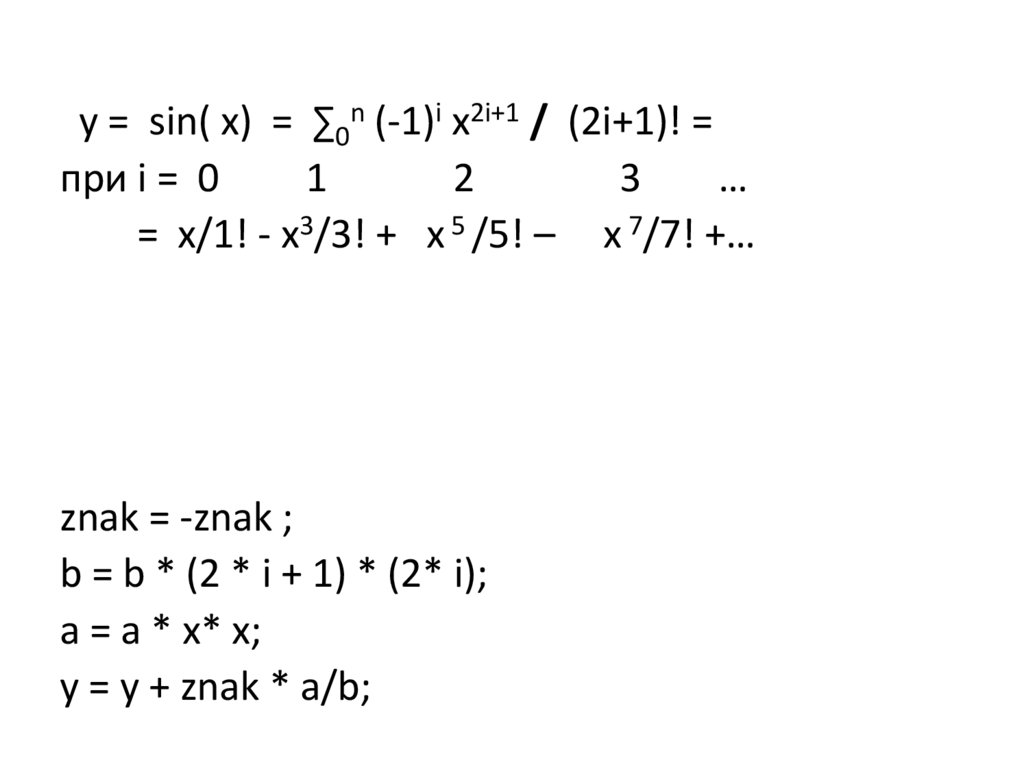
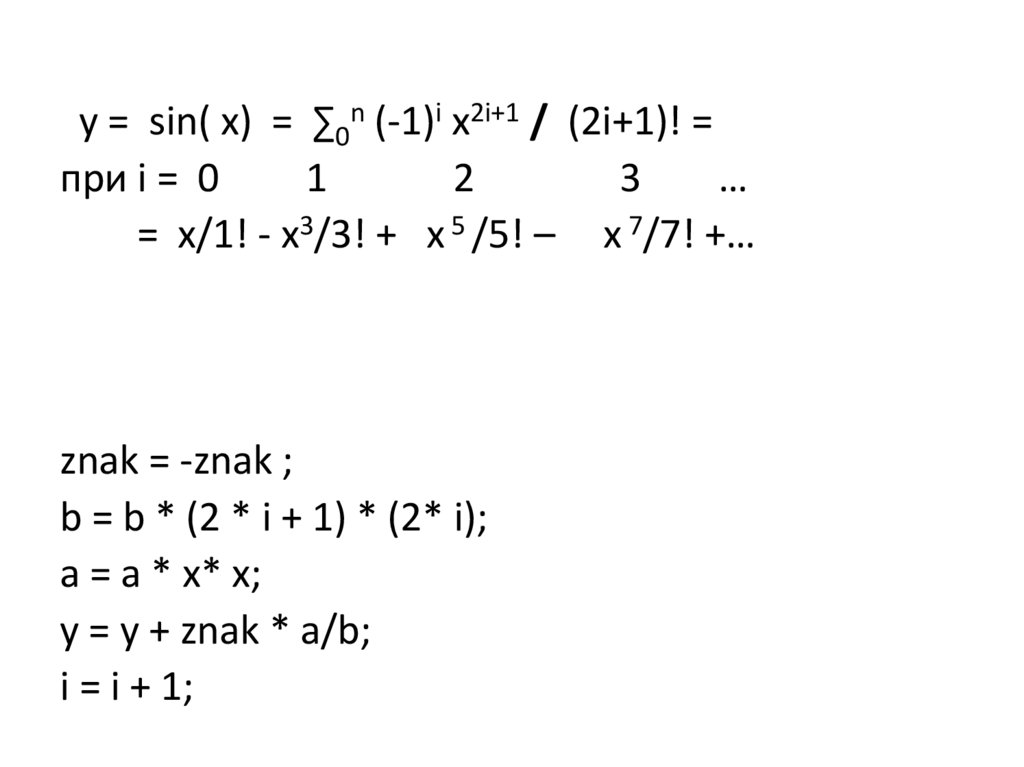
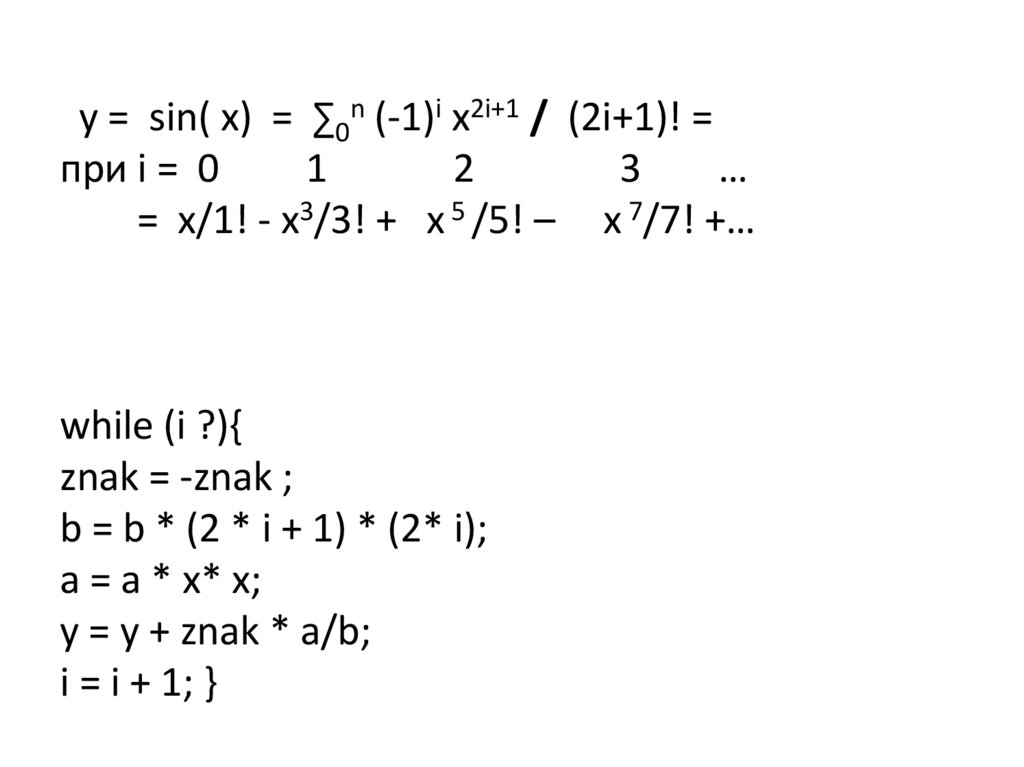
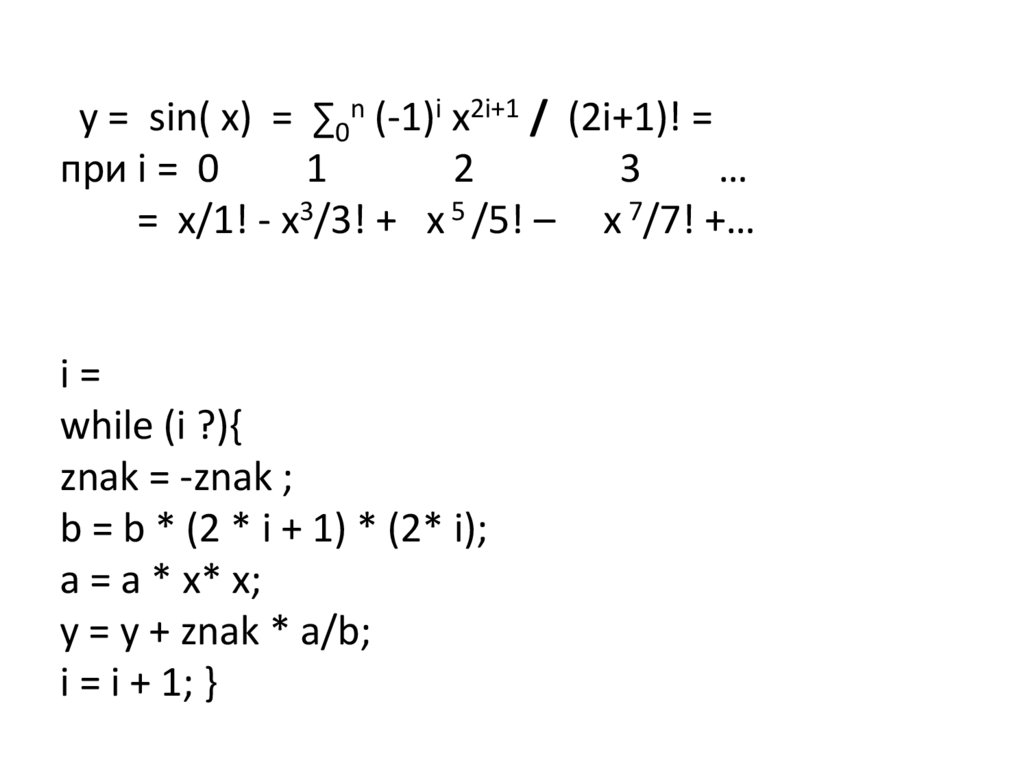
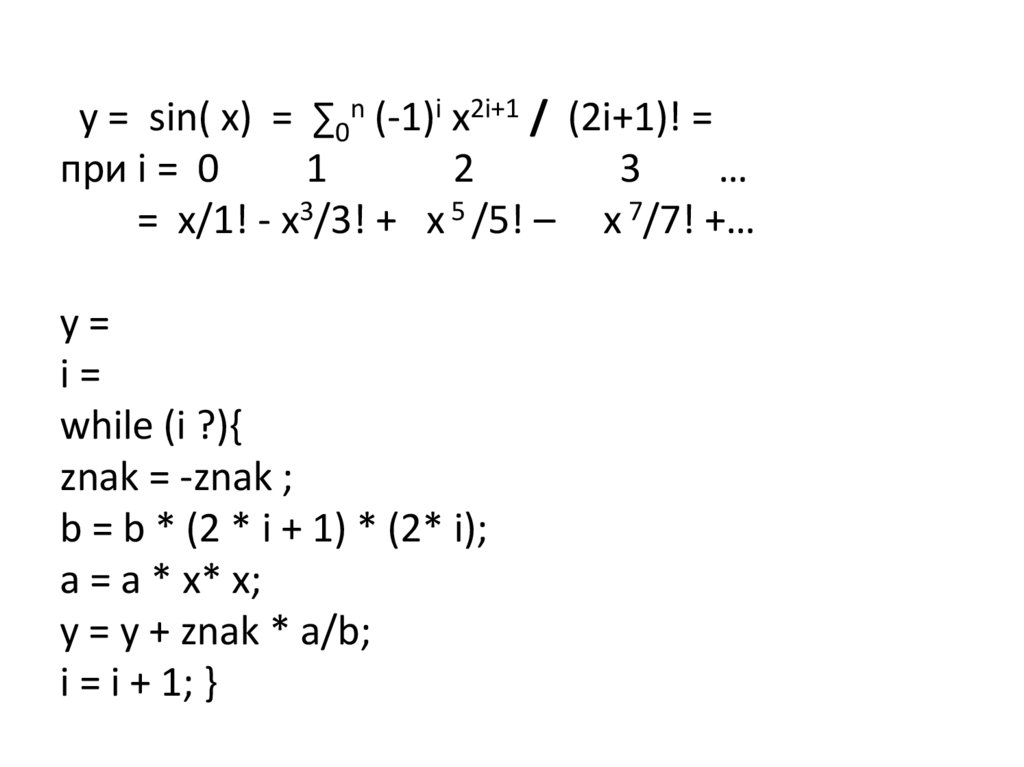
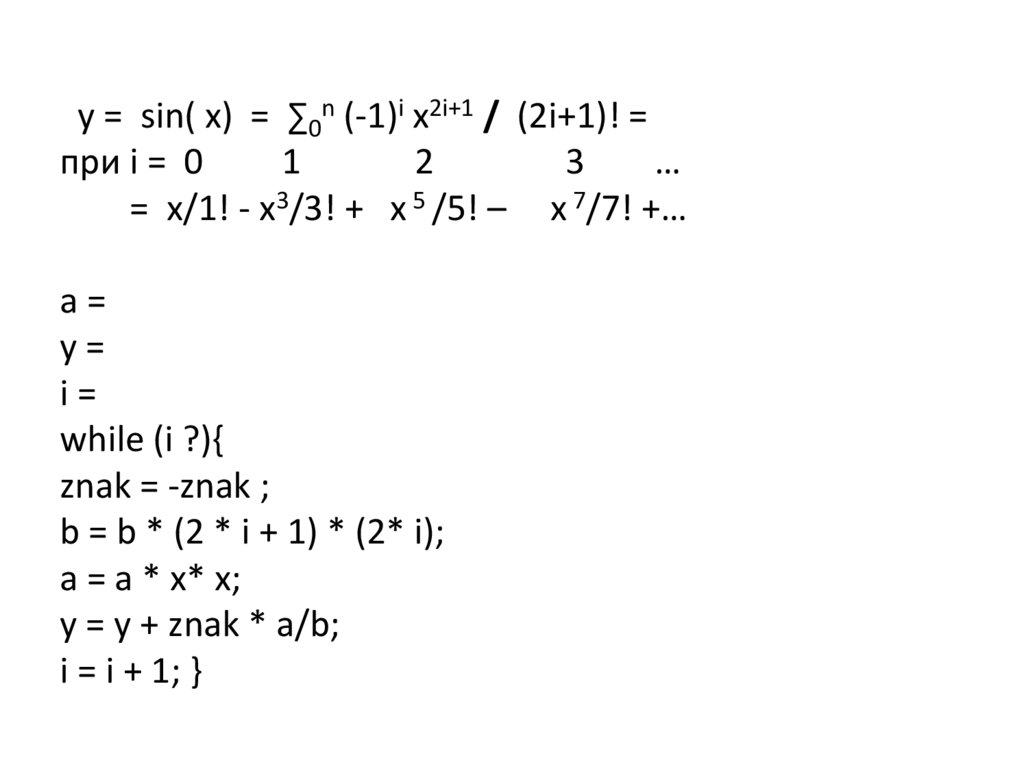
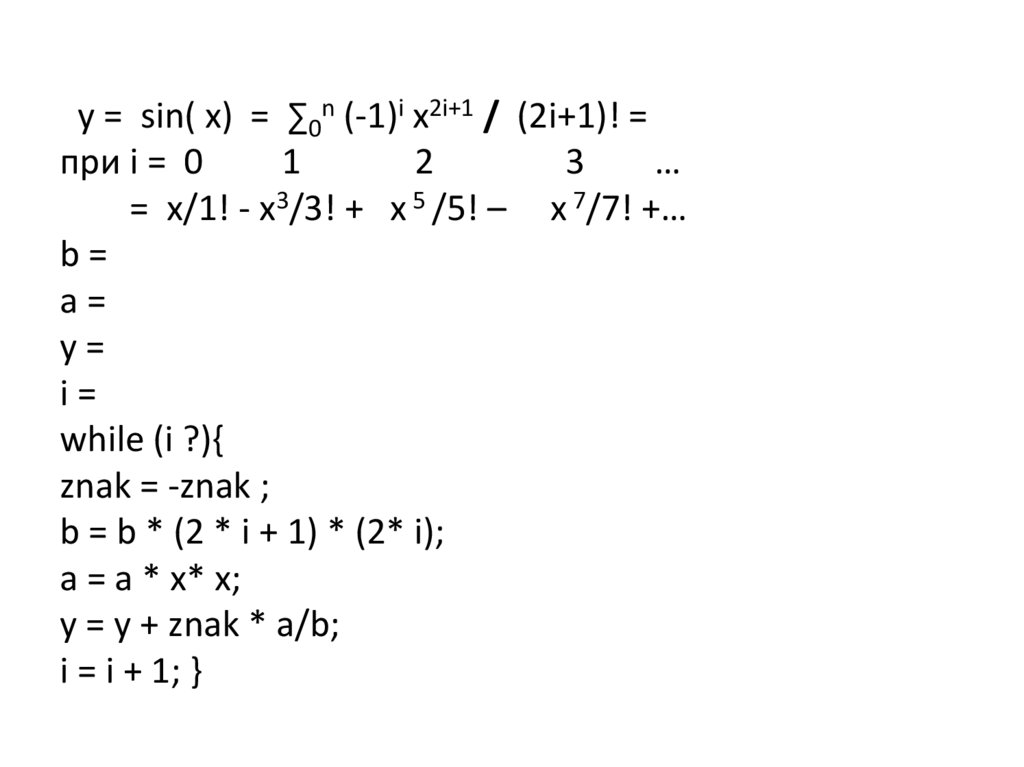

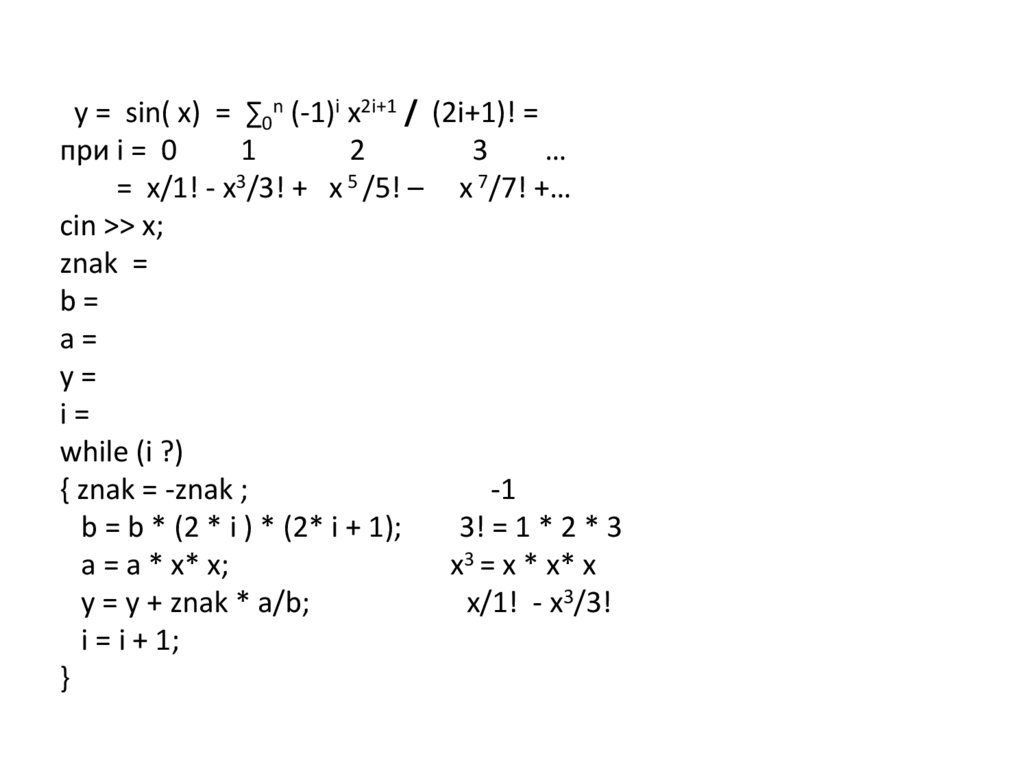
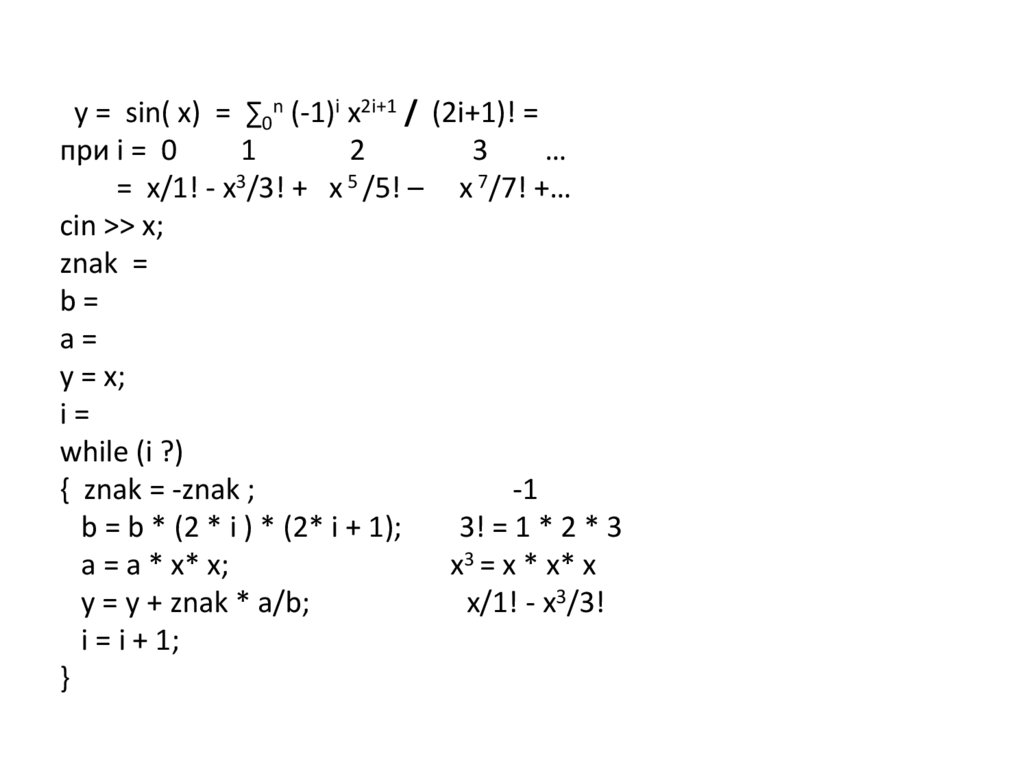
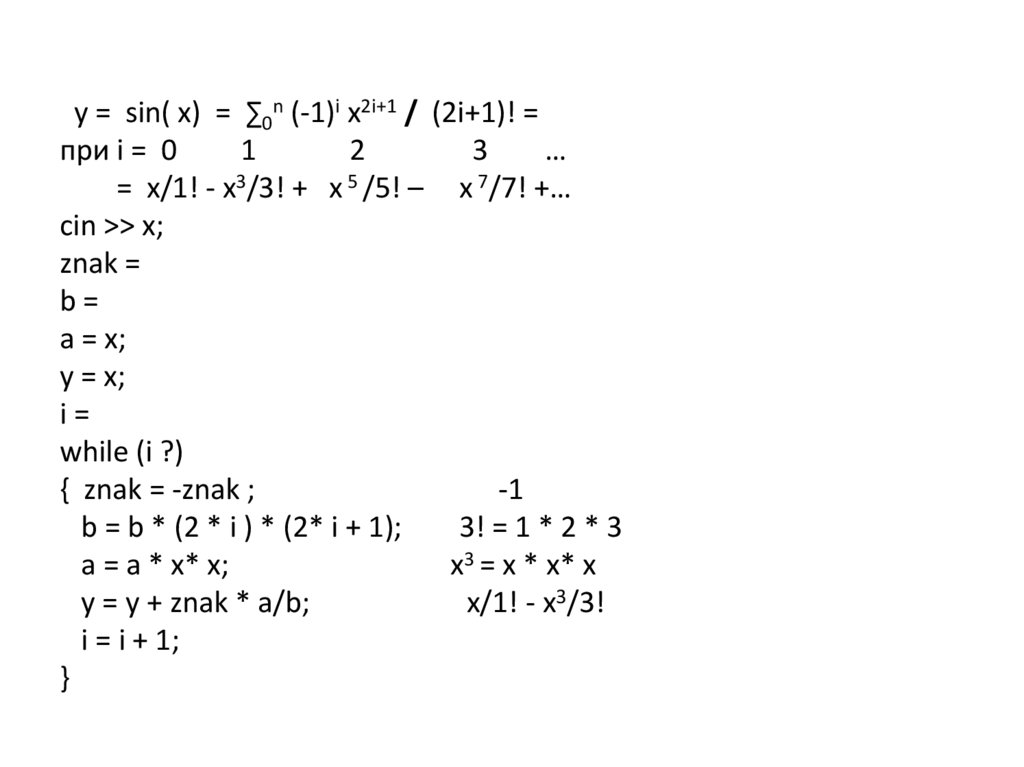
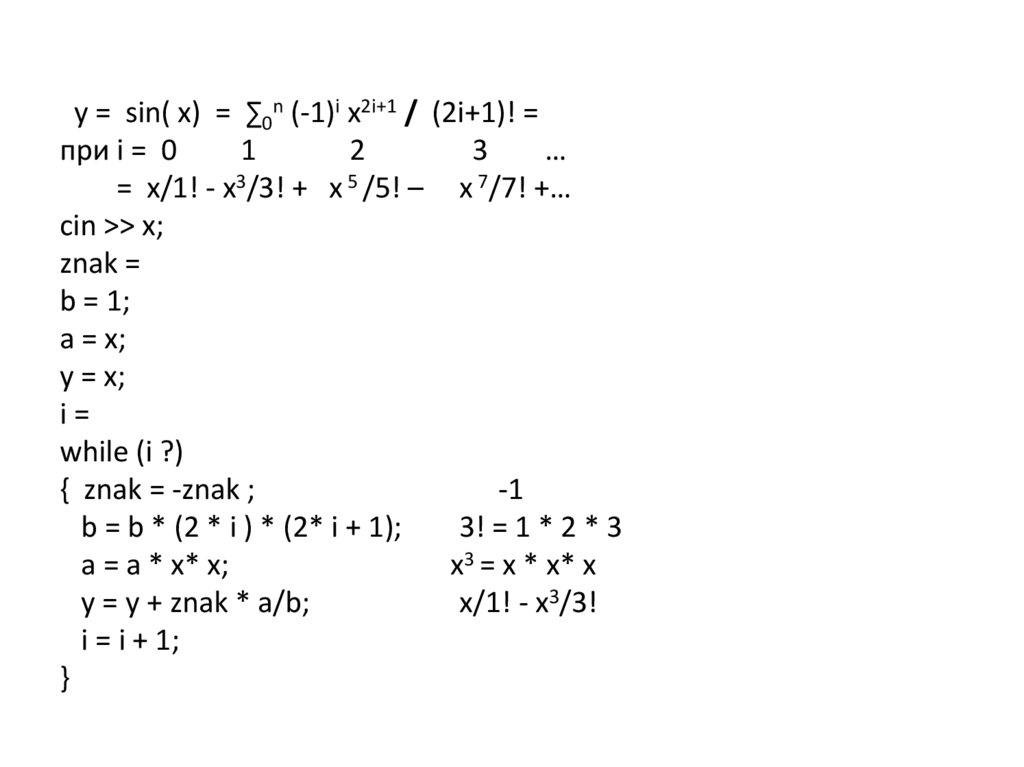
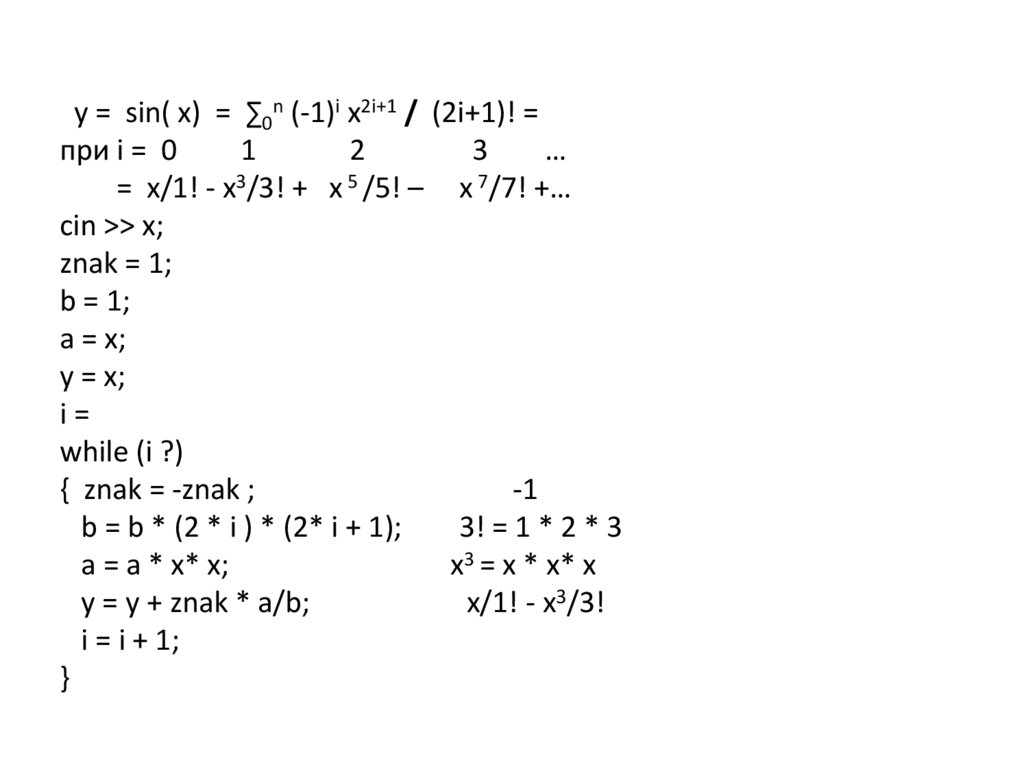
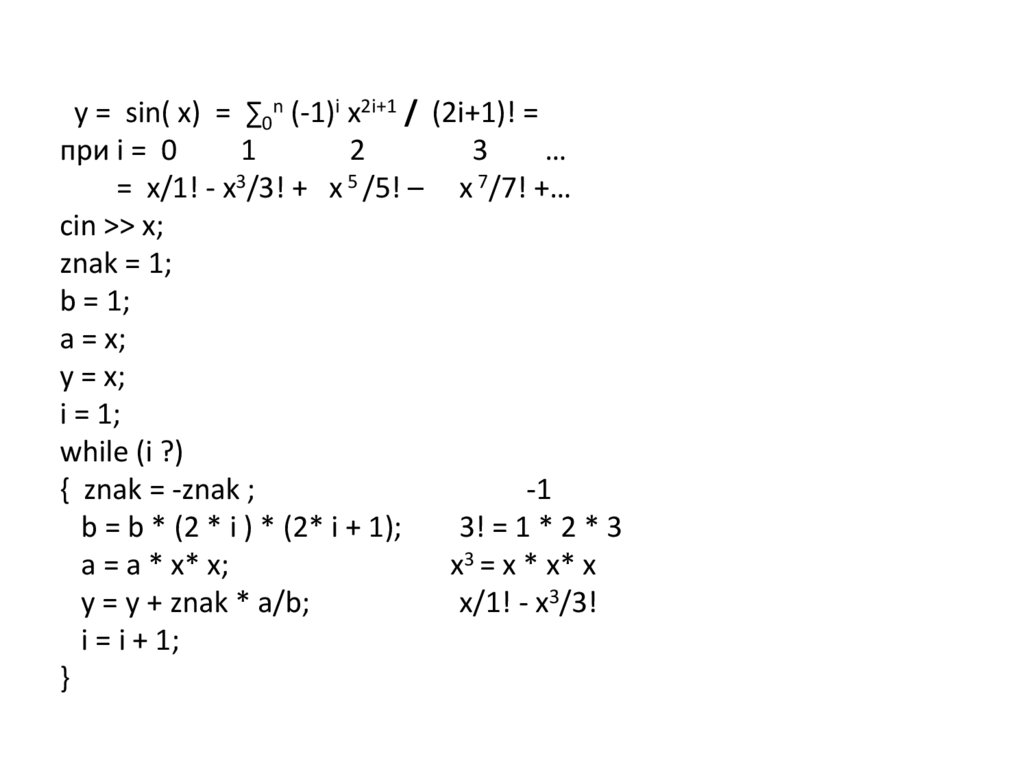
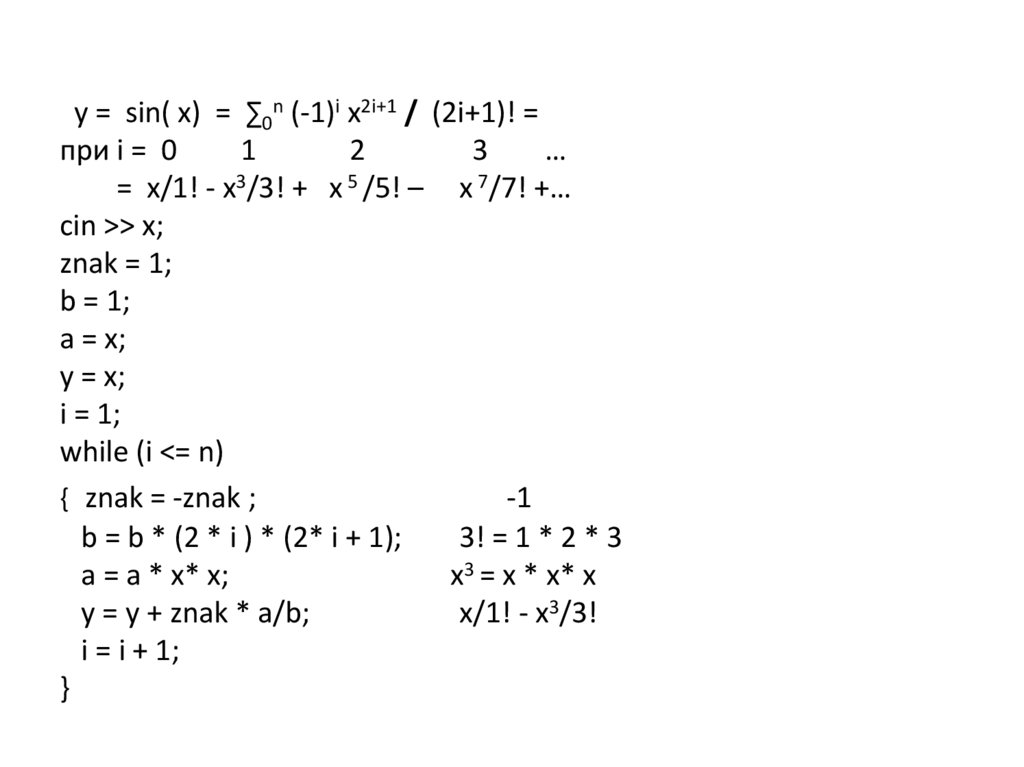
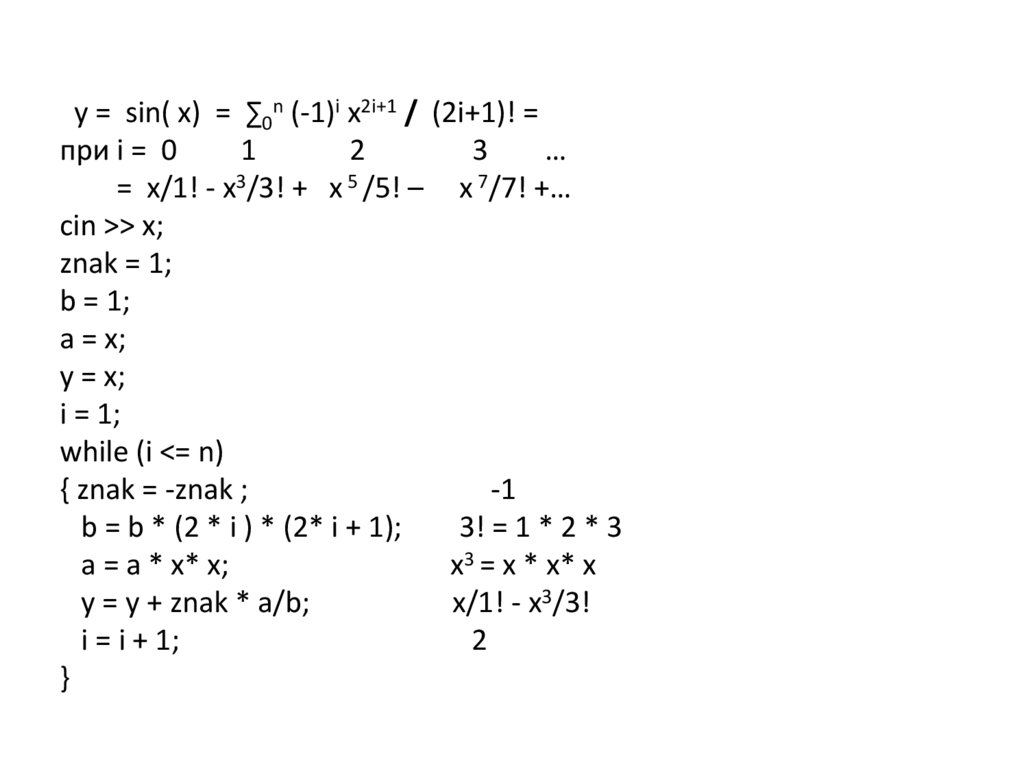
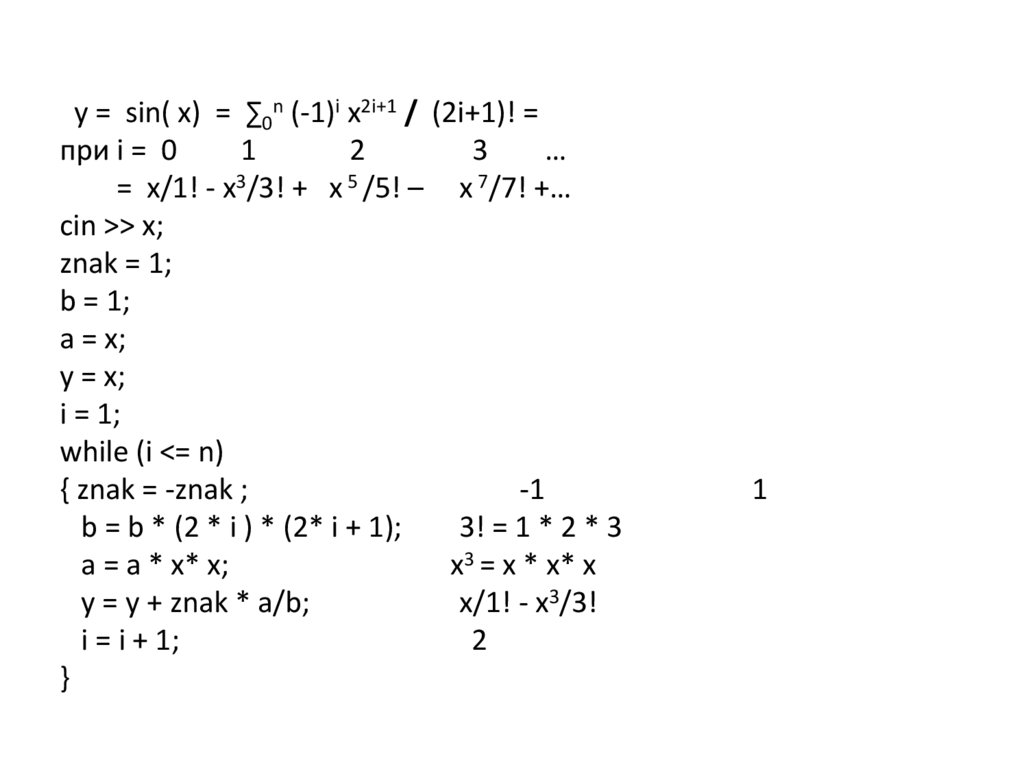
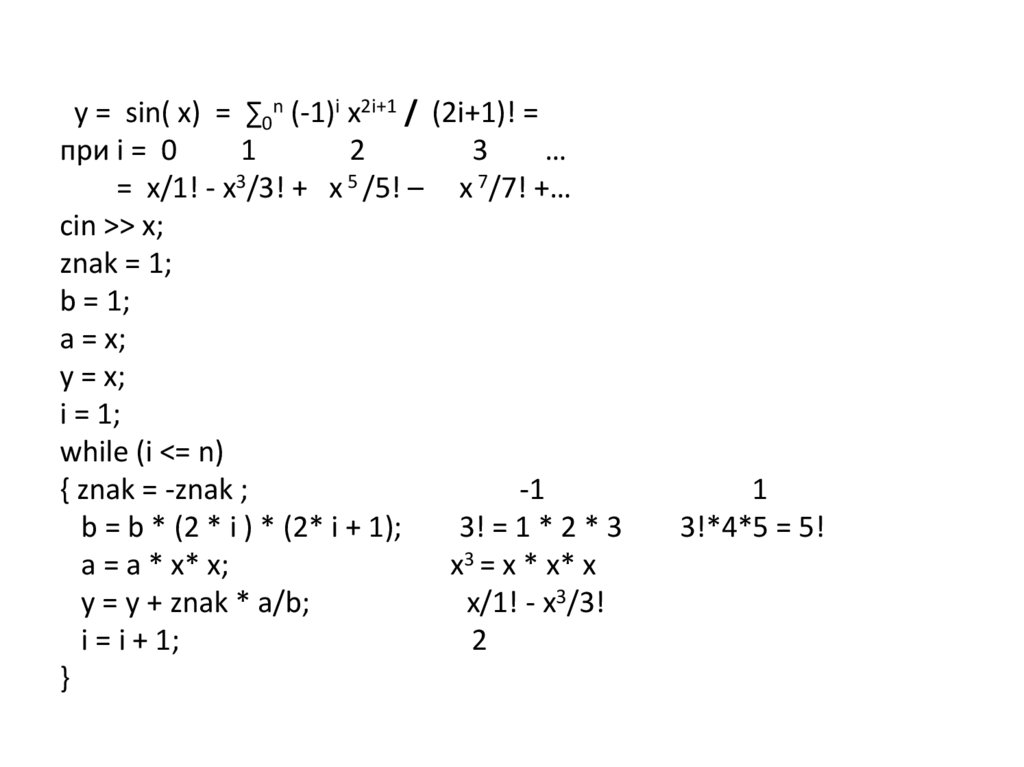
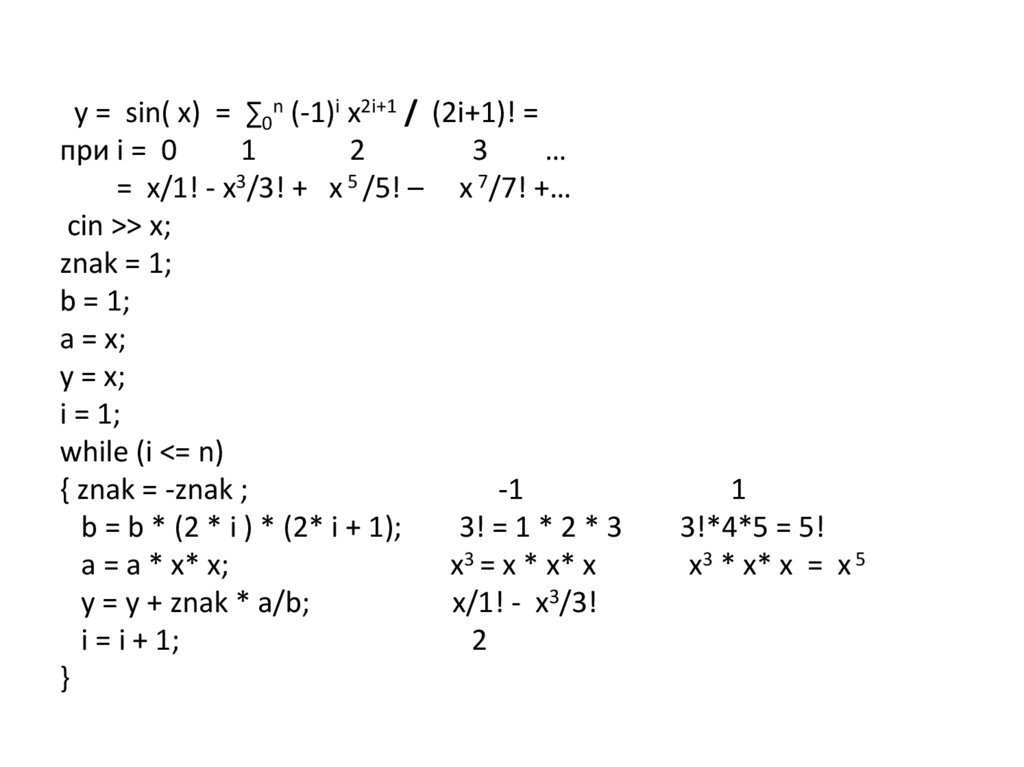
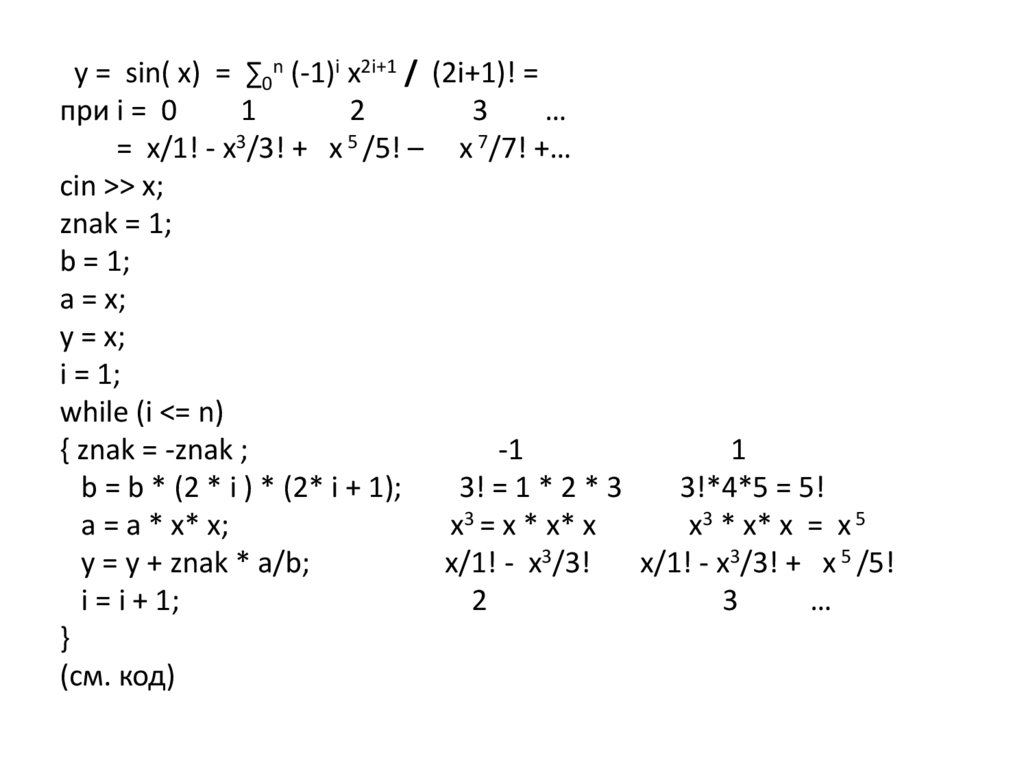















 Программирование
Программирование