Противоположное событие. Диаграммы Эйлера (Вероятности случайных событий. Сложение и умножение вероятностей)

1.

Противоположное
событие.
Диаграммы Эйлера
(Вероятности случайных
событий. Сложение и
умножение вероятностей)

2.

Напомним:
Случайный опыт (случайный эксперимент) - математическая абстракция,
описывающая реальный опыт, который может оканчиваться различными
событиями
Случайный опыт оканчивается каким-либо одним элементарным
событием. Какое именно элементарное событие наступает в данном опыте –
дело случая. Два различных элементарных
события одновременно
произойти не могут.
Случайное событие или просто событие – это некоторое множество (набор,
совокупность) элементарных событий.
Случайное событие A наступает, когда происходит какое - либо
элементарное событие, благоприятствующие событию A.

3.

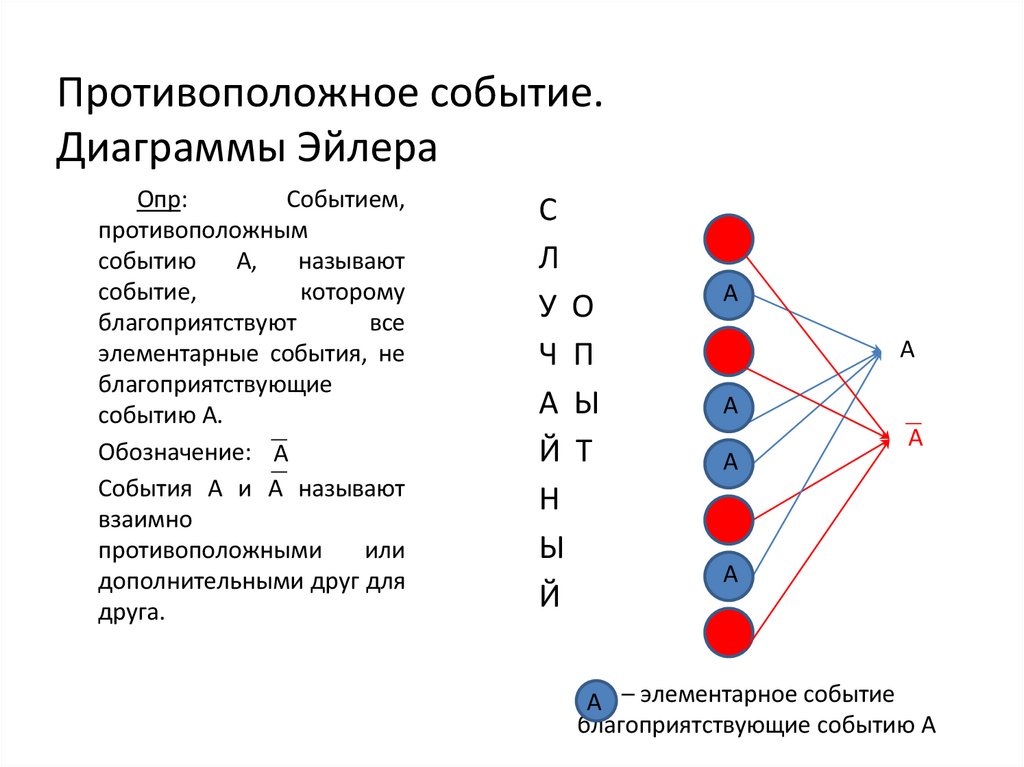
Противоположное событие.
Диаграммы Эйлера
Опр:
Событием,
противоположным
событию
А,
называют
событие,
которому
благоприятствуют
все
элементарные события, не
благоприятствующие
событию А.
Обозначение: А
События А и А называют
взаимно
противоположными
или
дополнительными друг для
друга.
С
Л
У О
Ч П
А Ы
Й Т
Н
Ы
Й
А
А
А
А
А
А
А – элементарное событие
благоприятствующие событию А

4.

Пример
Бросают игральную кость. Рассмотрим событие А «выпало число, большее 4».
Этому событию благоприятствуют элементарные события «выпала пятёрка» и «выпала
шестёрка». Не благоприятствуют событию А следующие элементарные события:
«выпала единица», «выпала двойка», «выпала тройка», «выпала четвёрка» (см. рис.).
Для события А противоположным событием А является событие «выпало число,
меньшее или равное четырём».
Событие А
Событие А
Взаимно противоположные события одновременно произойти не могут, но какое –
либо из них происходит обязательно. Поэтому
Р(А) + Р(А) = 1.
Иными словами, сумма вероятностей взаимно противоположных событий равна
единице.
Следовательно,
Р(А) = 1 – Р(А) и Р(А) = 1 – Р(А)
Из этих формул следует что для вычисления Р(А) достаточно знать Р(А) Это свойство
во многих случаях оказывается полезным.

5.

Свойства противоположных событий
1) Если В = А, то А = В
2) Взаимно противоположные события одновременно произойти не могут,
но какое – либо из них происходит обязательно.
Р(А) + Р(А) = 1
3) Для вычисления Р(А) достаточно знать Р(А).
Р(А) = 1 – Р(А)
Р(А) = 1 – Р(А)

6.

Диаграммы Эйлера
Соотношения и связи между
событиями можно изобразить с
помощью схематических рисунков
– диаграмм Эйлера.
Если
нужно
изобразить
несколько событий, то рисуют
несколько фигур – по одной для
каждого события. При этом
фигуры могут располагаться по –
разному, показывая, как связаны
между собой данные события.
Событие А
А
Событие А,
противоположное
А

7.

Упражнение 1:
В случайном эксперименте 20 элементарных событий. Событию А благоприятствуют 12
из них. Сколько элементарных событий благоприятствуют событию А?
Решение
ссылк
Упражнение 2:
В некотором случайном опыте может произойти событие K. Найдите вероятность
события K, если вероятность события K равна:
А) 0,4; Б) 0,85; В) 0,13; Г) ; Д) p.
ссылка
Решение
Упражнение 3:
Докажите, что события A и B не могут быть противоположны, если P(A) = 0,7, а P(B)=
0,44.
Решение
ссылка
Упражнение 4:
Могут ли быть противоположными события C и D, если:
А) P(C) = 0,12; P(D) = 0,78; Б) P(C) = 0,14; P(D) = 0,86; В) P(C) =
; P(D) =
, где >
>0, > 0; Г) P(C) = 0,5 + n; P(D) = 0,5 – n; где - 0,5 < n < 0,5; Д) P(C) = 0,8 + m; P(D) = 0,8 – m,
где – 0,2 < m < 0,2; Е*) P(C) =
Решение
; P(D) =
, где a > 0,b > 0
ссылка

8.

Упражнение 5:
Бросают одну игральную кость. Событие A состоит в том, что:
А) Выпала шестёрка;
Б) Выпало чётное число очков;
В) Выпало число очков кратное 3.
Для каждого случая перечислите элементарные события, благоприятствующие событию A,
опишите событие A словами и найдите P(A).
ссылка
Решение
Упражнение 6:
На диаграмме Эйлера (см. рис.) изображены события А и В. Нарисуйте диаграмму в
тетради и выделите на ней событие D, которое состоит в том, что:
А) Событие А наступило, а В – нет
Б) Событие В наступило, а А – нет
В) Наступило событие А
Г) Наступило событие В
А
Решение
В
ссылка