Алгоритмы и решения комбинаторных задач «Раскраски»

1.

Муниципальное бюджетное образовательное учреждение
«Мари-Турекская средняя общеобразовательная школа»
Алгоритмы и решения комбинаторных задач по теме
«Раскраски»
Автор проекта: Матвеева Доминика Александровна
учащаяся 10 класса
Руководитель: Ветлужских Светлана Борисовна
учитель математики и информатики
Мари-Турек, 2025

2.

Актуальность
Изучение алгоритмов, решающих комбинаторные задачи по
раскраскам, позволяет эффективно решать реальные проблемы,
внедрять новые технологии и разрабатывать оптимизированные
системы. Это открывает новые горизонты для разработки новых
эффективных алгоритмов, что является важным для развития наук
и техники.

3.

Цель проекта: изучить алгоритмы решения
комбинаторных задач.
Задачи проекта:
1. изучить литературу по теме проекта;
2. рассмотреть традиционные методы решения задач;
3. анализировать современные подходы и методики решения задач;
4. подобрать примеры алгоритмов для решения комбинаторных
задач.

4.

Комбинаторные задачи – это проблемы, которые требуют выбора
объектов из заданного множества для оптимизации определенного
критерия. Она изучает, как организовать, выбрать и
структурировать объекты под определенные условия.
Раскраски включают распределение вершин,
граней или других элементов по категориям
с учетом определенных правил. Задача
заключается в присвоении цветов элементам
некоторого множества, так чтобы
удовлетворились определенные правила или
ограничения. Основная цель – минимизация
количества используемых цветов, что
представляет собой достаточно трудную
задачу.

5.

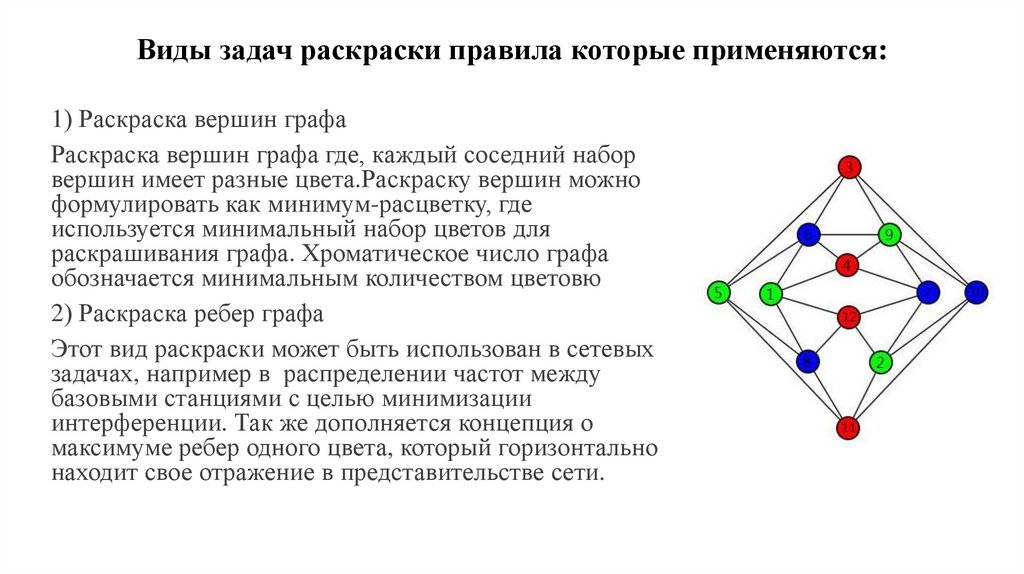
Виды задач раскраски правила которые применяются:
1) Раскраска вершин графа
Раскраска вершин графа где, каждый соседний набор
вершин имеет разные цвета.Раскраску вершин можно
формулировать как минимум-расцветку, где
используется минимальный набор цветов для
раскрашивания графа. Хроматическое число графа
обозначается минимальным количеством цветовю
2) Раскраска ребер графа
Этот вид раскраски может быть использован в сетевых
задачах, например в распределении частот между
базовыми станциями с целью минимизации
интерференции. Так же дополняется концепция о
максимуме ребер одного цвета, который горизонтально
находит свое отражение в представительстве сети.

6.

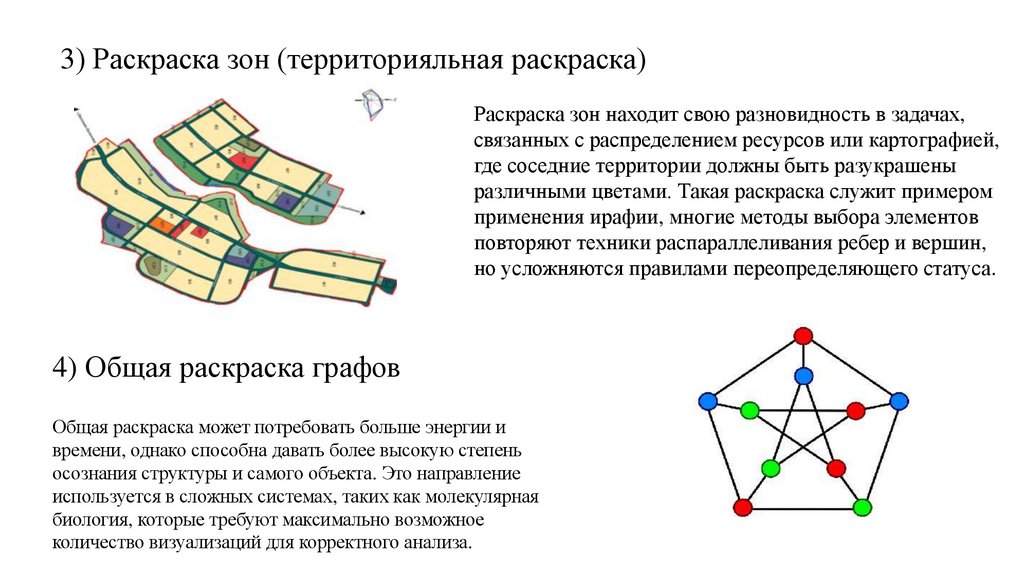
3) Раскраска зон (территорияльная раскраска)
Раскраска зон находит свою разновидность в задачах,
связанных с распределением ресурсов или картографией,
где соседние территории должны быть разукрашены
различными цветами. Такая раскраска служит примером
применения ирафии, многие методы выбора элементов
повторяют техники распараллеливания ребер и вершин,
но усложняются правилами переопределяющего статуса.
4) Общая раскраска графов
Общая раскраска может потребовать больше энергии и
времени, однако способна давать более высокую степень
осознания структуры и самого объекта. Это направление
используется в сложных системах, таких как молекулярная
биология, которые требуют максимально возможное
количество визуализаций для корректного анализа.

7.

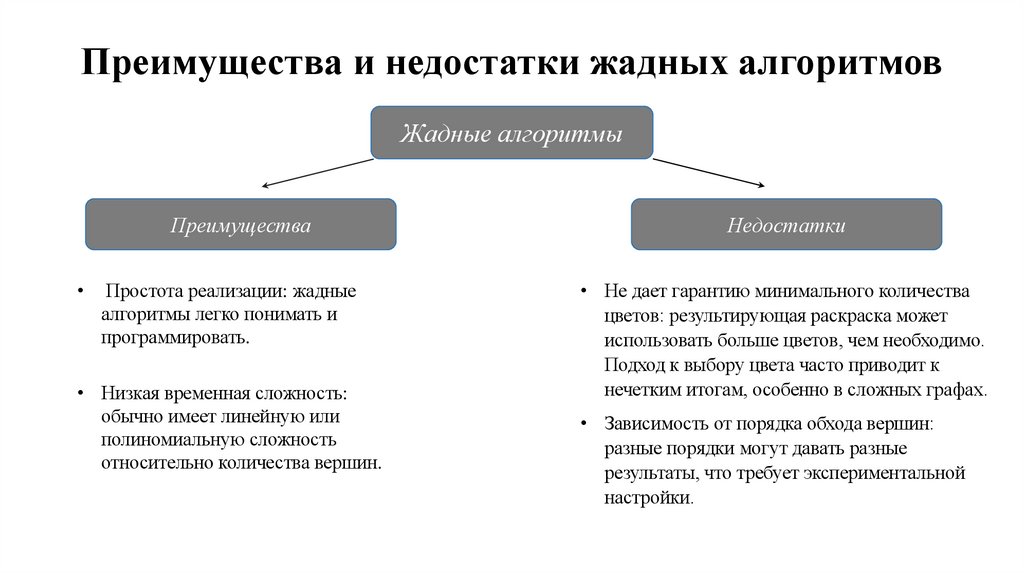
Преимущества и недостатки жадных алгоритмов
Жадные алгоритмы
Преимущества
Недостатки
Простота реализации: жадные
алгоритмы легко понимать и
программировать.
• Не дает гарантию минимального количества
цветов: результирующая раскраска может
использовать больше цветов, чем необходимо.
Подход к выбору цвета часто приводит к
нечетким итогам, особенно в сложных графах.
• Низкая временная сложность:
обычно имеет линейную или
полиномиальную сложность
относительно количества вершин.
• Зависимость от порядка обхода вершин:
разные порядки могут давать разные
результаты, что требует экспериментальной
настройки.

8.

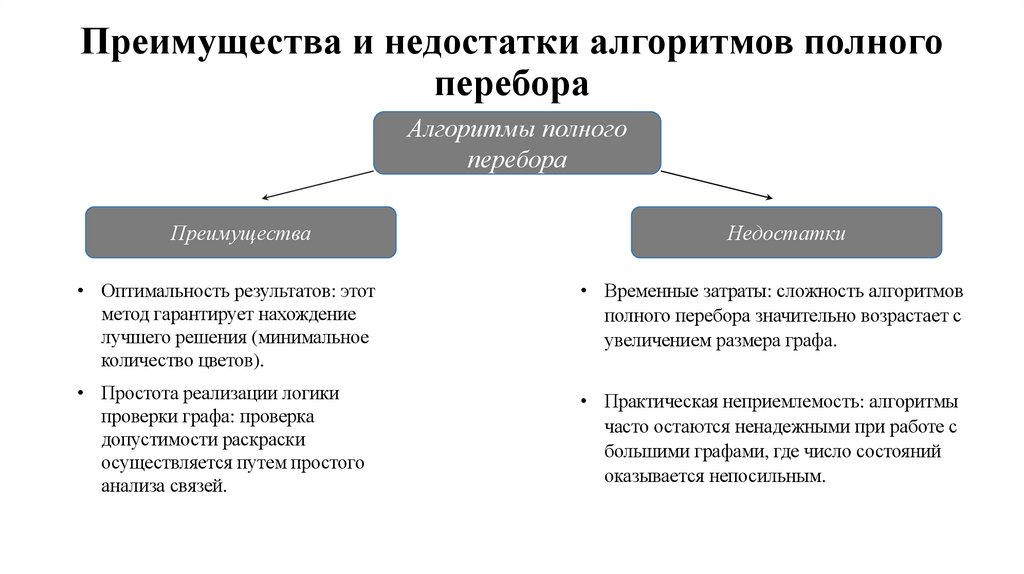
Преимущества и недостатки алгоритмов полного
перебора
Алгоритмы полного
перебора
Преимущества
Недостатки
• Оптимальность результатов: этот
метод гарантирует нахождение
лучшего решения (минимальное
количество цветов).
• Временные затраты: сложность алгоритмов
полного перебора значительно возрастает с
увеличением размера графа.
• Простота реализации логики
проверки графа: проверка
допустимости раскраски
осуществляется путем простого
анализа связей.
• Практическая неприемлемость: алгоритмы
часто остаются ненадежными при работе с
большими графами, где число состояний
оказывается непосильным.

9.

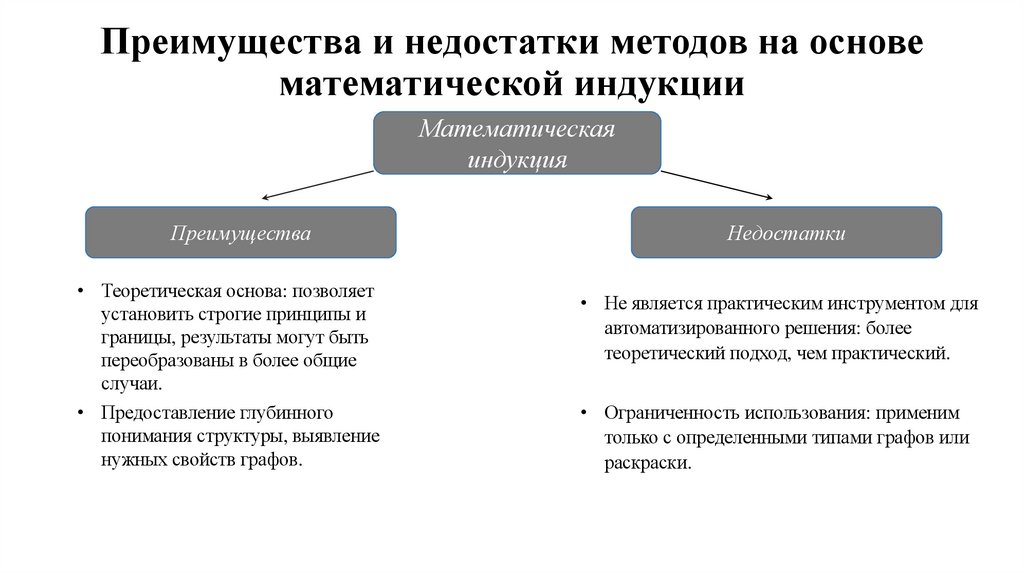
Преимущества и недостатки методов на основе
математической индукции
Математическая
индукция
Преимущества
Недостатки
• Теоретическая основа: позволяет
установить строгие принципы и
границы, результаты могут быть
переобразованы в более общие
случаи.
• Не является практическим инструментом для
автоматизированного решения: более
теоретический подход, чем практический.
• Предоставление глубинного
понимания структуры, выявление
нужных свойств графов.
• Ограниченность использования: применим
только с определенными типами графов или
раскраски.

10.

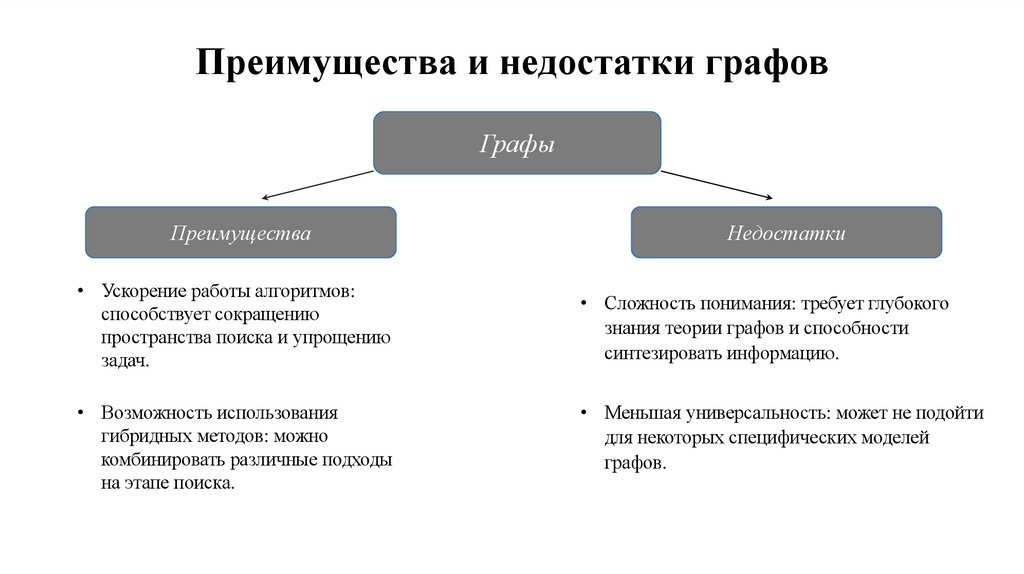
Преимущества и недостатки графов
Графы
Преимущества
• Ускорение работы алгоритмов:
способствует сокращению
пространства поиска и упрощению
задач.
• Возможность использования
гибридных методов: можно
комбинировать различные подходы
на этапе поиска.
Недостатки
• Сложность понимания: требует глубокого
знания теории графов и способности
синтезировать информацию.
• Меньшая универсальность: может не подойти
для некоторых специфических моделей
графов.

11.

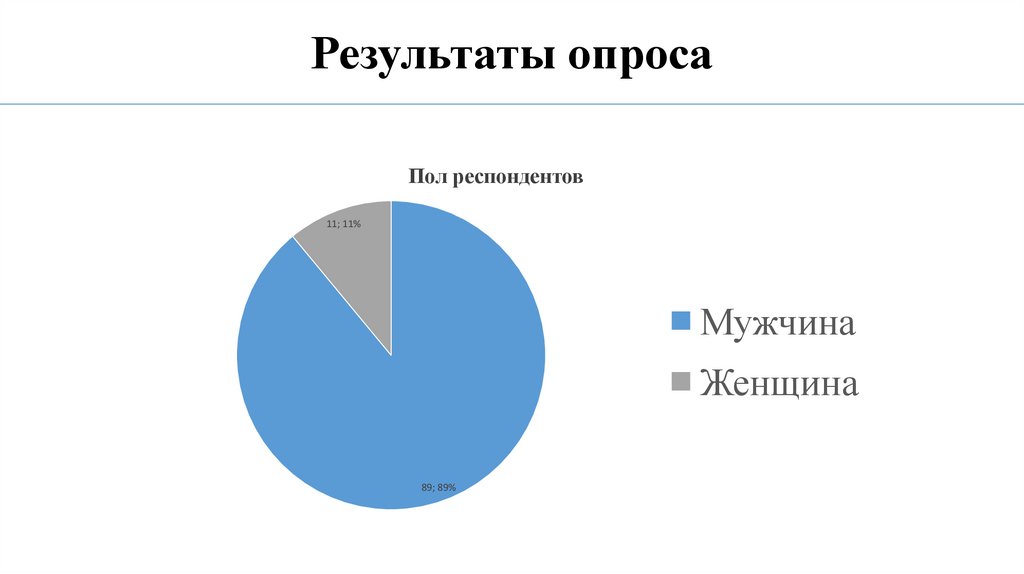
Результаты опроса
Пол респондентов
11; 11%
Мужчина
Женщина
89; 89%

12.

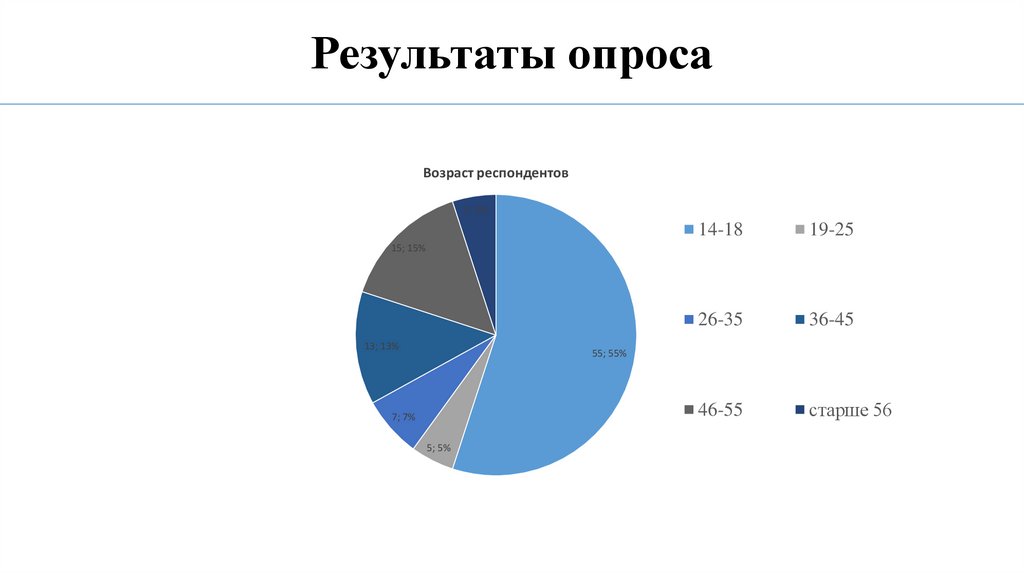
Результаты опроса
Возраст респондентов
5; 5%
14-18
19-25
26-35
36-45
46-55
старше 56
15; 15%
13; 13%
55; 55%
7; 7%
5; 5%