Кинематика твердого тела

1.

Кинематика твердого тела
План
1. Вращательное движение
2. Поступательное движение твердого
тела
3. Плоскопараллельное (плоское)
движение

2.

Задача кинематики твердого тела
состоит в изучении движения тела в
целом, а также в изучении движения
каждой точки этого тела.
Вид
формул
для
определения
кинематических характеристик движения
тела будет зависеть от вида движения.

3.

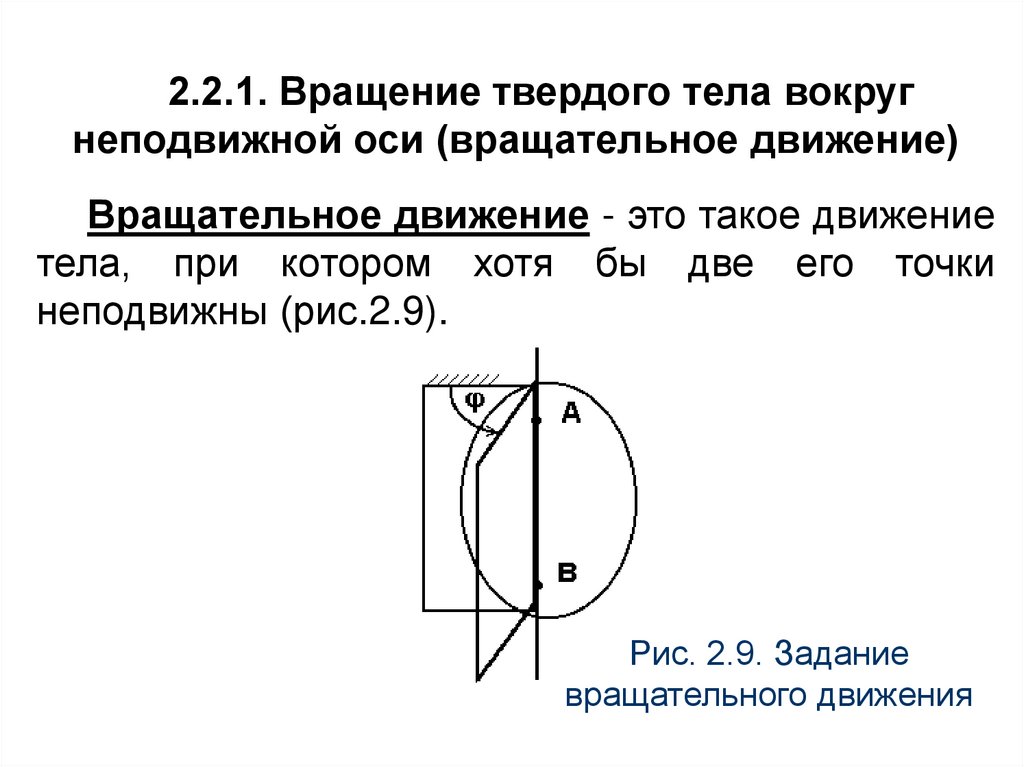
2.2.1. Вращение твердого тела вокруг
неподвижной оси (вращательное движение)
Вращательное движение - это такое движение
тела, при котором хотя бы две его точки
неподвижны (рис.2.9).
Рис. 2.9. Задание
вращательного движения

4.

Прямая, соединяющая эти точки, называется
осью вращения.
Поскольку тело является абсолютно твердым, то
все точки, лежащие на оси вращения, будут
неподвижны.
Задать вращательное движение можно с
помощью угла поворота , который
отсчитывается от неподвижной полуплоскости,
полуплоскостью, жестко связанной с телом
f t
(2.16)

5.

Угол измеряется в радианах (в одном обороте
содержится 2 радиан или 360 градусов).
Характеристикой быстроты вращения служит
угловая скорость - ω (омега).
Средняя угловая скорость равна отношению
угла поворота к промежутку времени, за который
произошел этот поворот.

6.

Если за промежуток времени t t1 t0 тело
cовершает поворот на угол 1 0 ,то
средней угловой скоростью тела за
промежуток времени будет величина, равная
1 0
.
ср
t1 t 0
t
(2.17)

7.

Мгновенной угловой скоростью называется
величина, к которой стремится средняя, если
промежуток времени стремится к нулю
то есть
lim ср lim
t 0
t 0 t
d
dt
(2.18)
Мгновенная угловая скорость равна
производной от угла поворота по времени.
Единица измерения угловой скорости – радиан,
1
деленный на секунду
рад / с 1 / с с

8.

В технике быстрота вращения измеряется в
оборотах в минуту. Обозначим эту величину
буквой n и назовем частотой вращения.
Так как в 1 обороте содержится 2 радиан, а в
минуте - 60 секунд, то
2 n
60
(2.19)

9.

Характеристикой быстроты изменения угловой
скорости служит угловое ускорение
(эпсилон).
Среднее угловое ускорение равно отношению
приращения угловой скорости к промежутку
времени, за который произошло это
приращение
c р
t
(2.20)

10.

Мгновенное угловое ускорение равно пределу, к
которому стремится среднее, если промежуток
времени стремится к нулю
lim ср lim
t 0
t 0 t
d d 2
2
dt
dt
(2.21)
то есть мгновенное угловое ускорение равно
первой производной по времени от угловой
скорости или второй производной от угла
поворота.

11.

Единица измерения углового ускорения
рад. 1
2 2 с 2
с
с
Угол поворота, угловая скорость и угловое
ускорение характеризуют вращательное
движение тела в целом.

12. Частные случаи вращательного движения:

1. Равномерное вращение.
2. Равнопеременное вращение.

13. Равномерное вращение.

Равномерным вращением тела
называется вращение, при котором
угловая скорость тела все время остается
постоянной (ω=const).
Из формулы (2.21) следует, что
тогда из (2.18)
0,
d dt С

14.

Проинтегрировав при φ0=0 получим:
t
Данная формула называется
равномерного вращения.
законом

15.

2. Равнопеременное вращение.
Равнопеременным называется такое
вращение тела, когда его угловое ускорение
во все время движения остается
постоянным (ε=Const ).
Из формулы (2.21) следует, что
d dt С
Проинтегрировав, получим закон изменения угловой
скорости

16.

Проинтегрировав, получим закон изменения
угловой скорости
t 0
Из формулы (2.18) следует, что
d dt
Проинтегрируем при φ0=0
d t 0 dt
получим закон равнопеременного вращения
t
0 t
2
2

17.

Вторая задача кинематики твердого тела:
определение кинематических характеристик
каждой его точки.
Для ее решения необходимо получить формулы
для определения скоростей и ускорений точек
вращающегося тела.
Рассмотрим какую-нибудь точку М твердого тела,
находящуюся на расстоянии h от оси вращения
(рис.2.10).

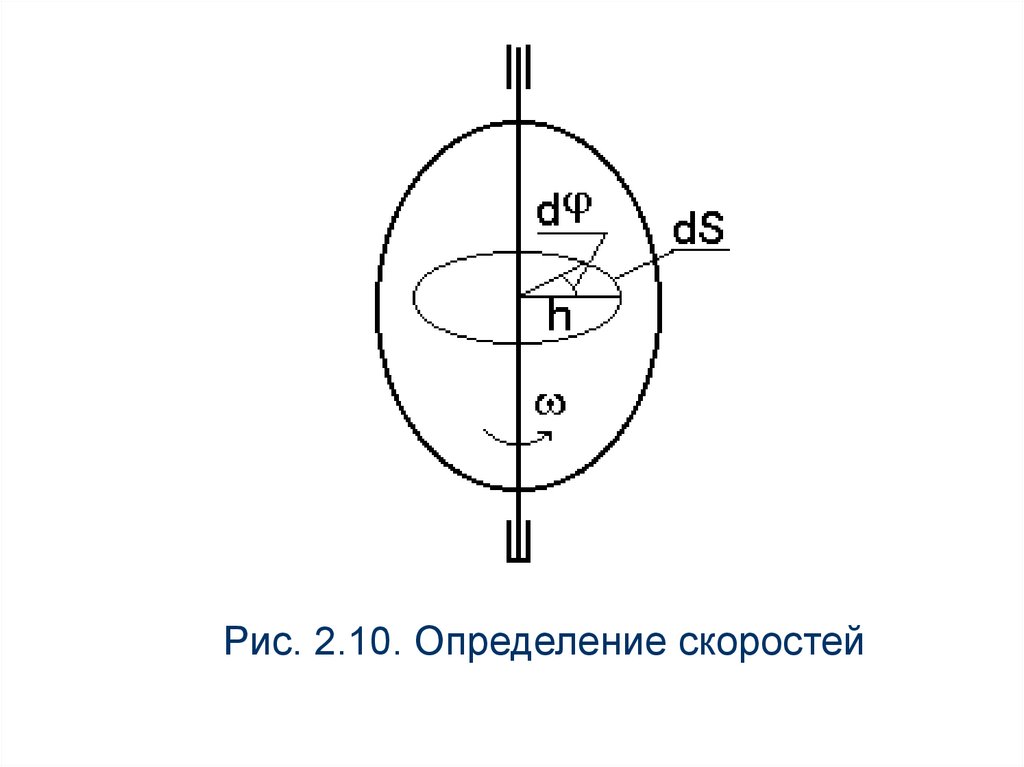
18.

Рис. 2.10. Определение скоростей

19.

При вращении тела точка М будет описывать
окружность радиуса h, плоскость которой
перпендикулярна оси вращения.
Если за время dt происходит элементарный
поворот тела на угол dφ, то точка М при этом
совершает вдоль своей траектории
элементарное перемещение ds h d . Тогда
числовое значение скорости будет равно
dS
d
V
h
dt
dt
откуда
V h
(2.22)

20.

то
есть
скорость
произвольной
точки
вращающегося
тела равна произведению
угловой скорости тела на расстояние от этой
точки до оси вращения.
Распределение скоростей
по диаметру сечения тела
показано на рис. 2.11.
Рис. 2.11. Скорости точек

21.

Для нахождения ускорения точки М воспользуемся
формулами
dV
a
dt
an
V
2
В нашем случае =h и, подставляя значения
скорости из (2.22), получим
d
а
h
dt
то есть
a h
(2.23)

22.

an
2 h2
h
откуда
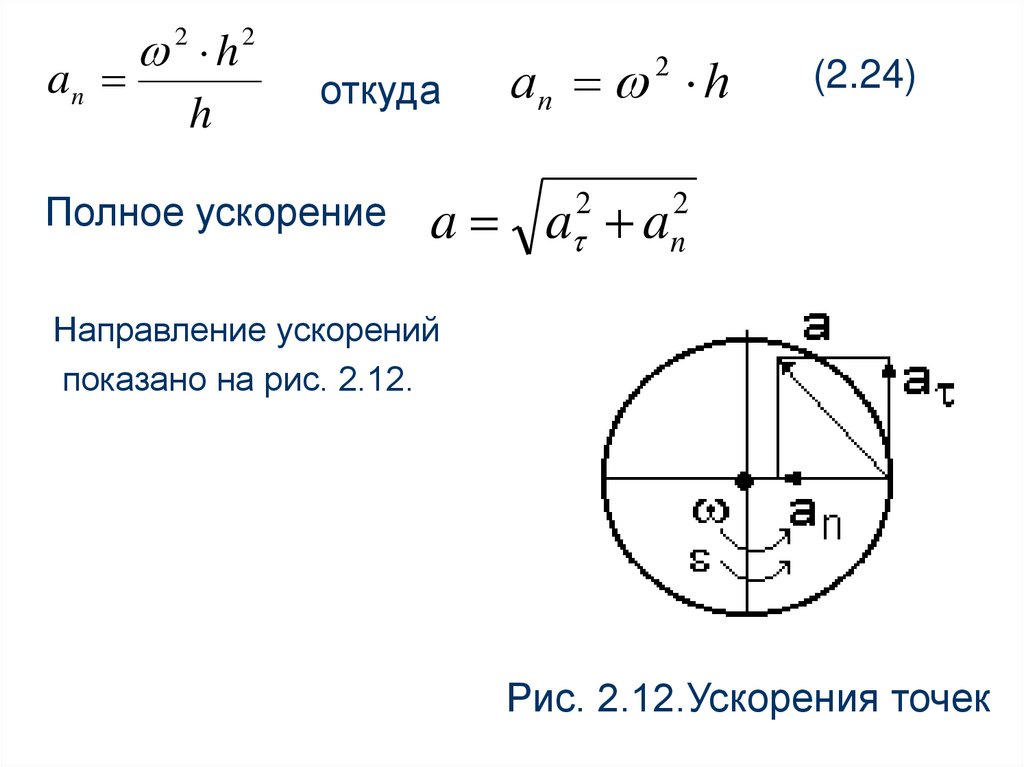
Полное ускорение
аn h
2
a a a
2
(2.24)
2
n
Направление ускорений
показано на рис. 2.12.
Рис. 2.12.Ускорения точек

23.

Пример. Определить скорость и ускорение конца
секундной стрелки часов длиной 2 см.
Решение. Секундная стрелка делает один оборот
в минуту, поэтому ее угловая скорость
2
pa .
n 0,105
60
c
Скорость и ускорение точки найдутся по формулам
V h
a h
an h
2

24.

Учитывая, что угловое ускорение стрелки равно
нулю, так как угловая скорость ее постоянна, а
расстояние от конца стрелки до оси вращения
h=2cм=0,02м, находим
V 0,105 0,02 0,0021 м/с.
a =0 м/с2.
a an l 0,105 0,02 0,00022
2
2
м/с2.

25.

Пользуясь полученными формулами, можно
произвести кинематический расчет простейших
механических передач.
Цель этого расчета - определение зависимости
между угловыми скоростями звеньев.
Передаточным отношением называется
отношение угловых скоростей ведущего и
ведомого звеньев
1
i12
2
(2.25)

26.

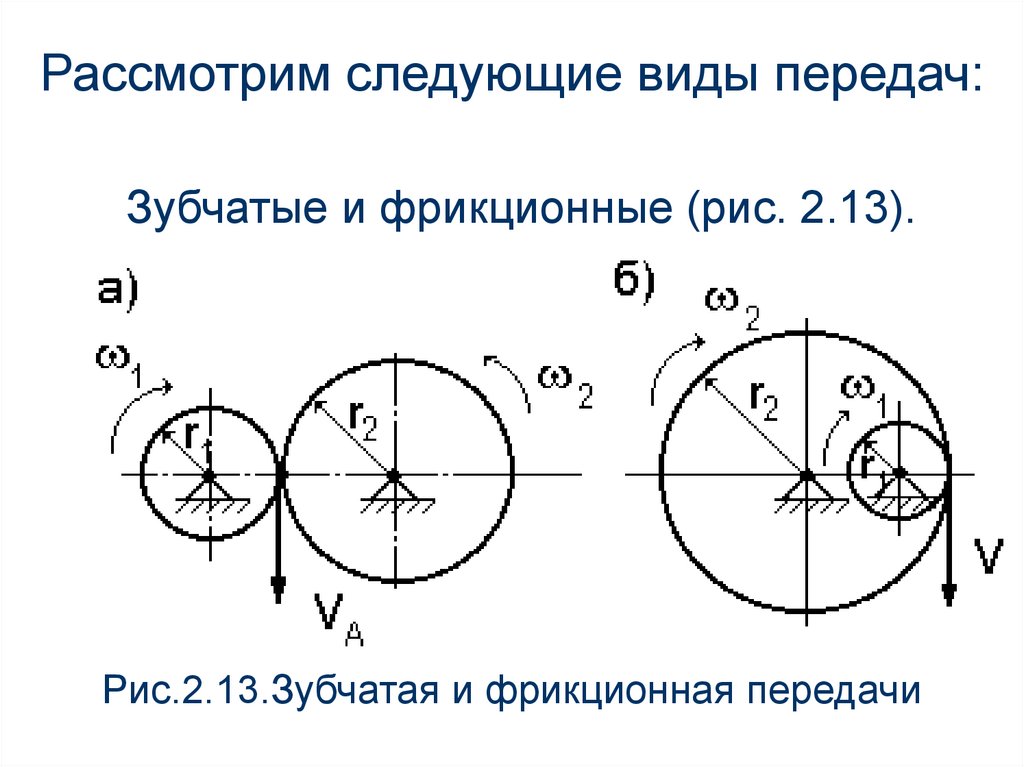
Рассмотрим следующие виды передач:
Зубчатые и фрикционные (рис. 2.13).
Рис.2.13.Зубчатая и фрикционная передачи

27.

Скорость точки касания колес равна скоростям
точек на их ободе, отсюда имеем:
VA 1r1 2 r2
Таким образом, передаточное отношение будет
равно
1 r2
i12
2 r1
(2.26)
Так как количество зубьев пропорционально
радиусам колес, то
z1
i12
z2
где
(2.27)
z1 и z 2 - количество зубьев на каждом из колес.

28.

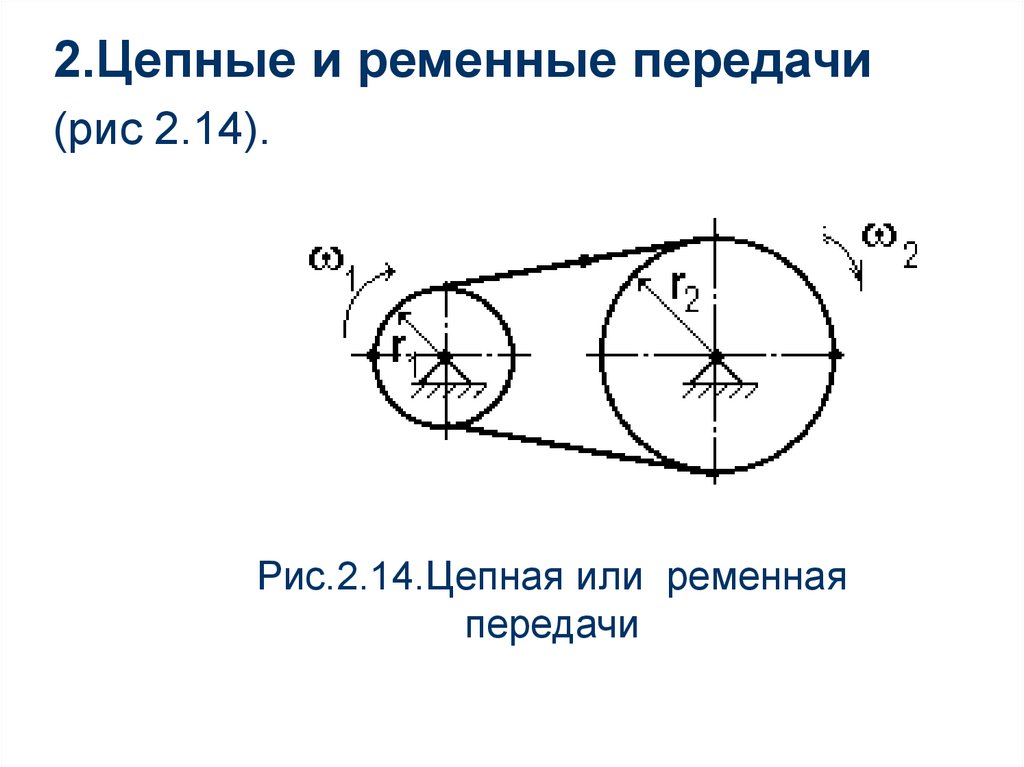
2.Цепные и ременные передачи
(рис 2.14).
Рис.2.14.Цепная или ременная
передачи

29.

Скорость точек ремня или цепи равна скоростям
точек на ободах ведомого и ведущего звеньев,
поэтому, формулы для определения
передаточного отношения будут аналогичными
формулам (2.26) и (2.27):
r2
i12
r1
для ременных
z2
i12
z1
- для цепных

30. 2.2.2. Поступательное движение твердого тела.

Поступательным называется такое движение
твердого тела, при котором любая прямая, жестко
связанная с телом, остается при его движении
параллельной самой себе.
Поступательное движение не следует смешивать с
прямолинейным.
При поступательном движении тела траектории его
точек могут быть любыми кривыми линиями.

31.

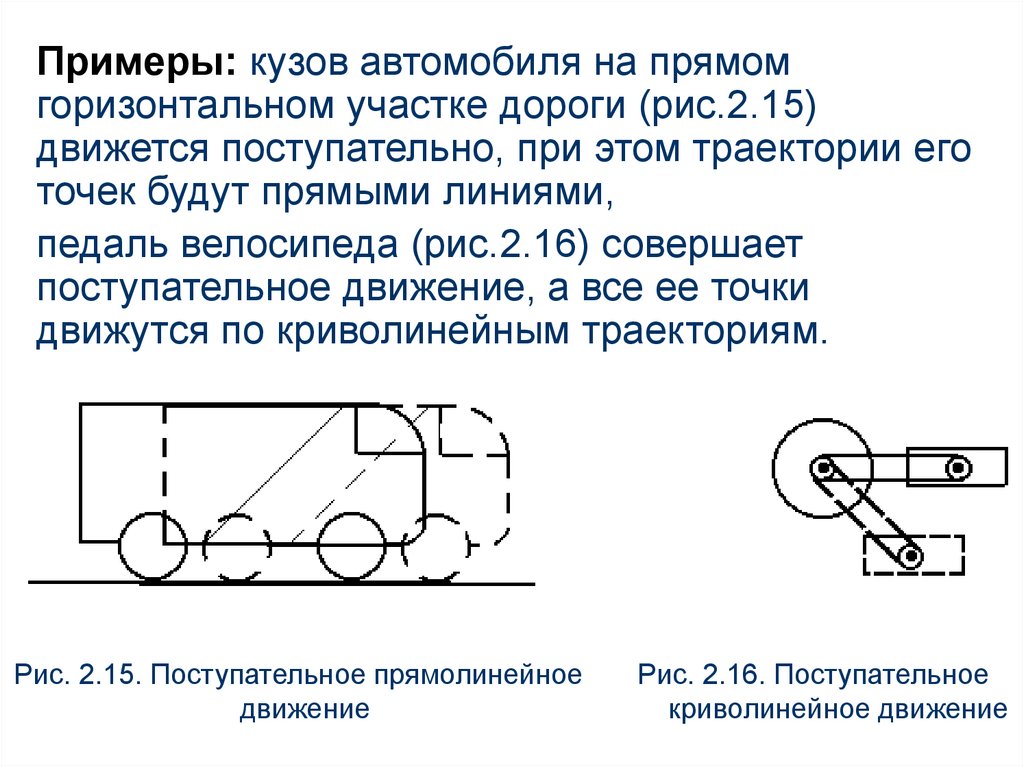
Примеры: кузов автомобиля на прямом
горизонтальном участке дороги (рис.2.15)
движется поступательно, при этом траектории его
точек будут прямыми линиями,
педаль велосипеда (рис.2.16) совершает
поступательное движение, а все ее точки
движутся по криволинейным траекториям.
Рис. 2.15. Поступательное прямолинейное
движение
Рис. 2.16. Поступательное
криволинейное движение

32.

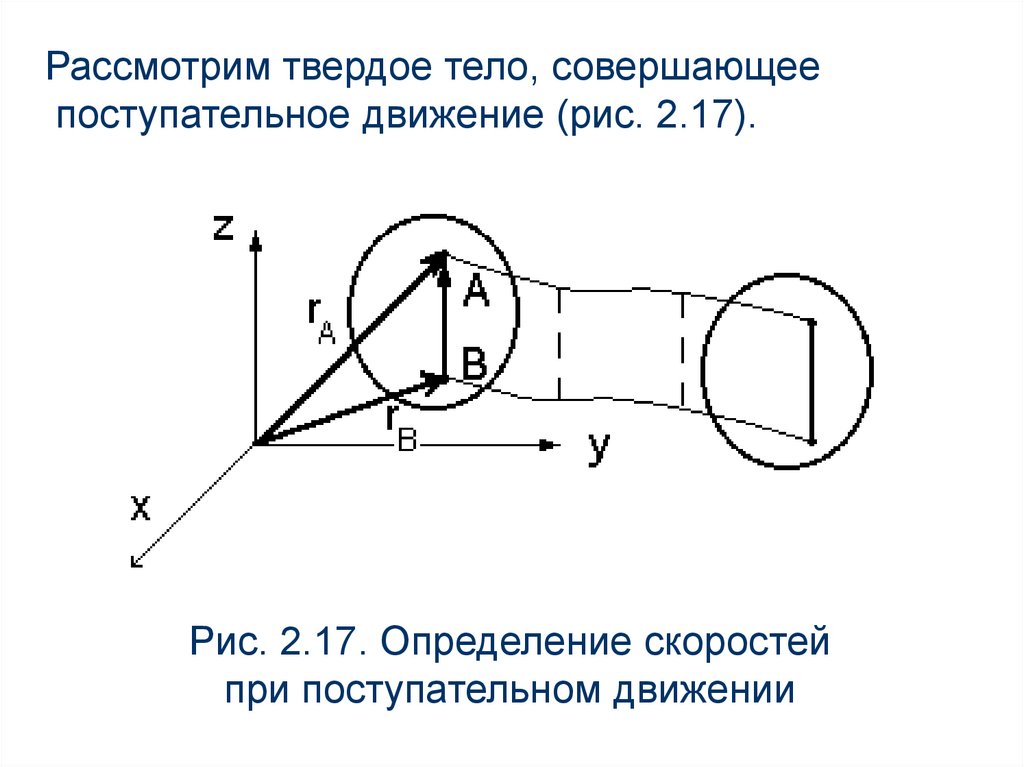
Рассмотрим твердое тело, совершающее
поступательное движение (рис. 2.17).
Рис. 2.17. Определение скоростей
при поступательном движении

33.

Выделим в нем произвольный отрезок АВ, который
при движении тела остается параллельным
самому себе. Из рисунка видно, что
rB rA AB
продифференцировав левую и правую части этого
уравнения по времени, получим
drB drA dAB
dt
dt
dt

34.

Так как вектор AB постоянен и по величине и
по направлению, то
отсюда:
dAB
0
dt
VB V A
продифференцировав это уравнение еще раз,
имеем
aB a A

35.

Таким образом, можно сделать вывод:
при поступательном движении твердого тела все
его точки движутся по одинаковым траекториям
и имеют одинаковые скорости и ускорения,
следовательно, для изучения движения всего
тела, достаточно изучить движение одной его
точки.

36.

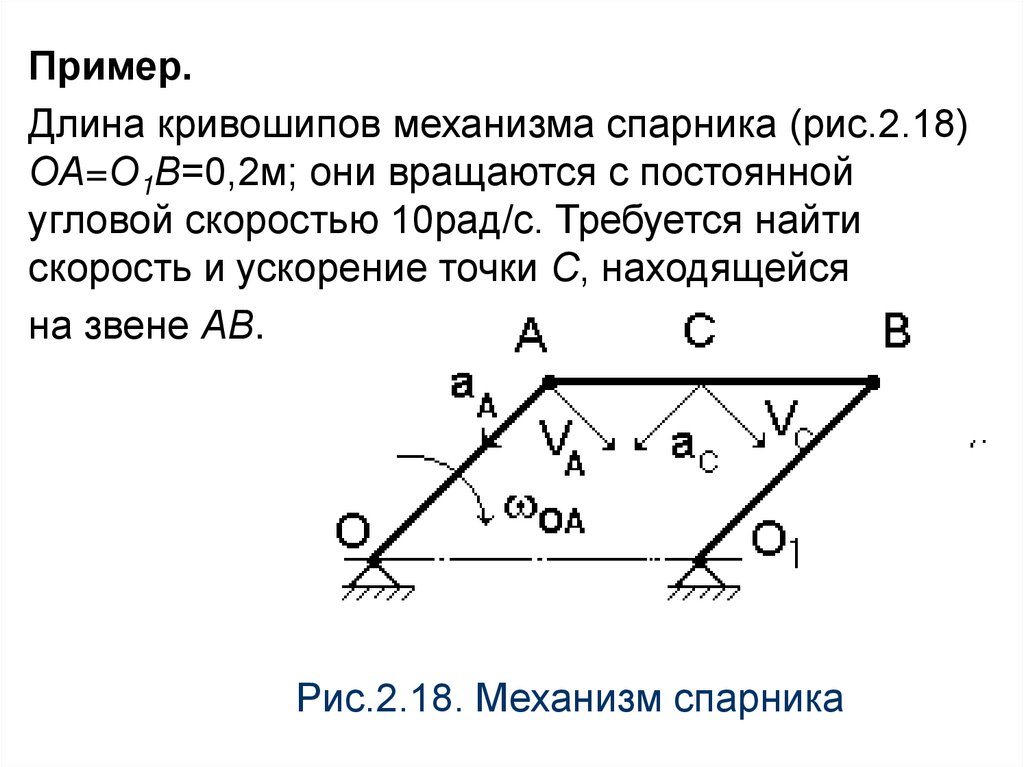
Пример.
Длина кривошипов механизма спарника (рис.2.18)
ОА=О1В=0,2м; они вращаются с постоянной
угловой скоростью 10рад/с. Требуется найти
скорость и ускорение точки С, находящейся
на звене АВ.
Рис.2.18. Механизм спарника

37.

Решение.
Звено АВ совершает поступательное
движение, поэтому скорости и ускорения всех его
точек одинаковы, в частности:
VC VA
ac a A
Поскольку точка А находится на конце звена ОА,
совершающего вращательное движение, то ее
скорость равна
м
VA м А ОА 10 0,2 2
с

38.

Ускорение точки А
a
касательное: A ОА 0
(так как ОА const ,то
ОА 0 ).
нормальное: a OA 10 0.2 20 м/с2.
n
A
2
OA
2
Полное ускорение точки А равно нормальному.
Направление скорости и ускорения точки С
показаны на рис 2.18.

39. Плоскопараллельное (плоское) движение твердого тела.

• Плоскопараллельное движение - это такое
движение твердого тела, при котором все его
точки движутся параллельно какой-нибудь
неподвижной плоскости.
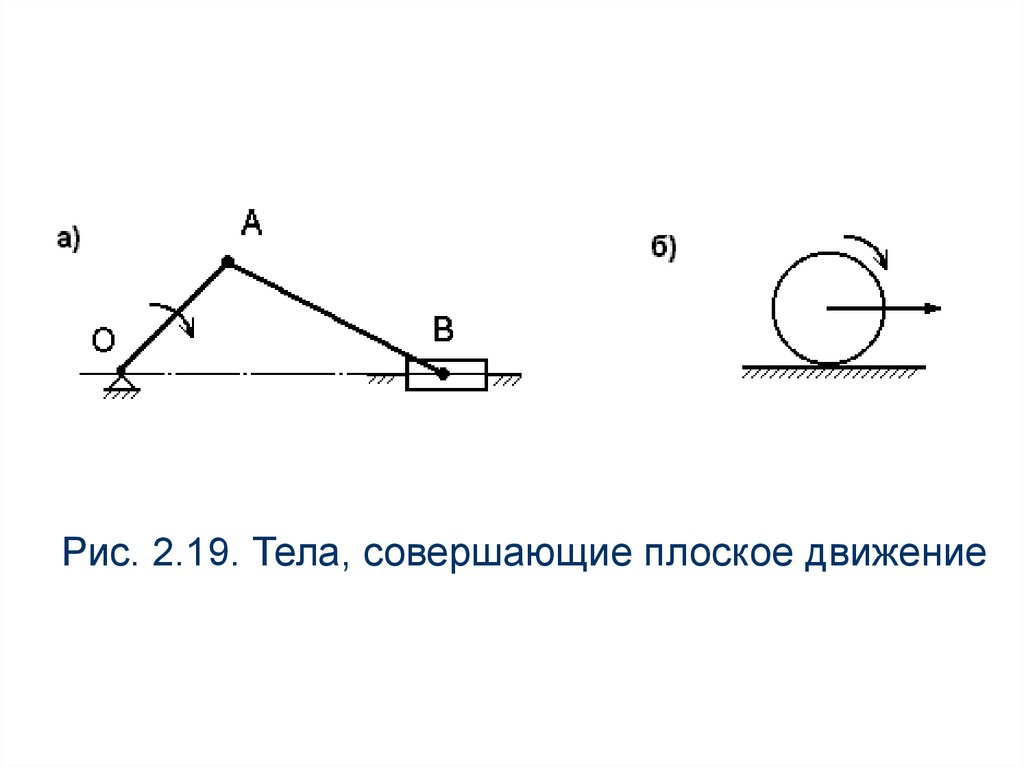
Плоское движение совершают многие части
механизмов и машин, например, шатун АВ в
кривошипно-ползунном механизме (рис. 2.19,а),
катящееся колесо на прямолинейном участке пути
(рис 2.19,б).

40.

Рис. 2.19. Тела, совершающие плоское движение

41.

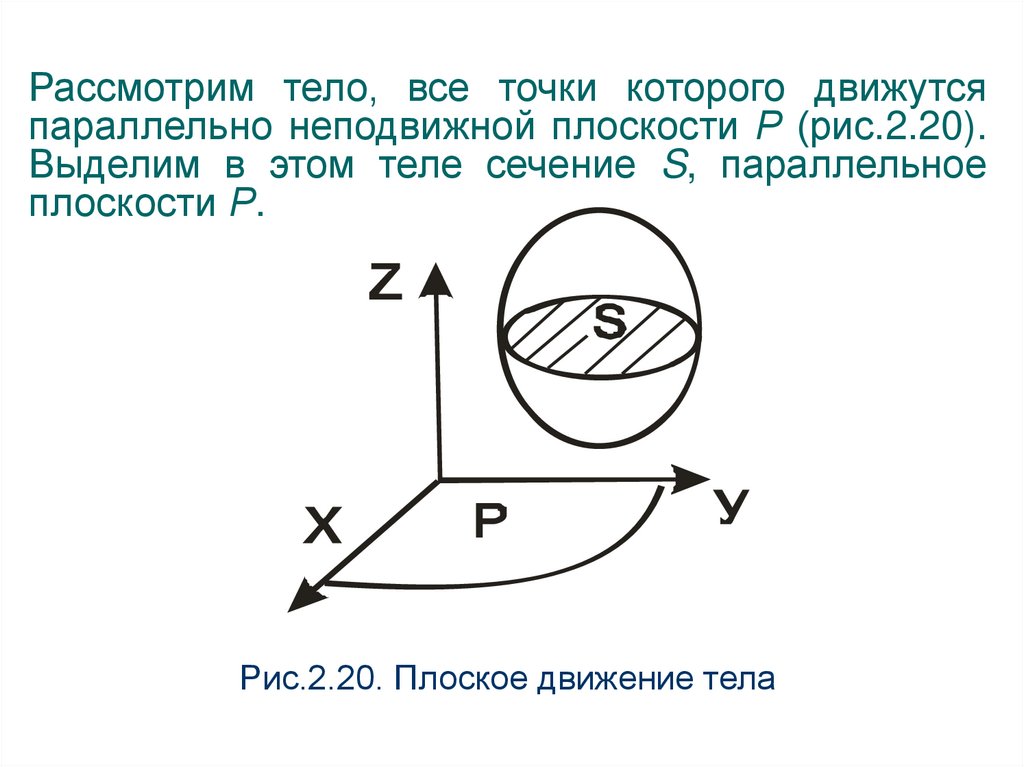
Рассмотрим тело, все точки которого движутся
параллельно неподвижной плоскости Р (рис.2.20).
Выделим в этом теле сечение S, параллельное
плоскости Р.
Рис.2.20. Плоское движение тела

42.

Для изучения движения всего тела достаточно
изучить движение этого сечения, поскольку
остальные точки тела жестко связаны с точками
этого сечения.
Для изучения движения в кинематике оно должно
быть задано.
Положение всего сечения определяет положение
произвольного отрезка АВ, которое, в свою
очередь, может быть задано при помощи
координат Х и У произвольной точки А и угла
поворота , который образует отрезок АВ с осью Х.

43.

Таким образом, для того, чтобы задать плоское
движение, необходимы три уравнения
X f (t ), y f (t ), f (t ).
A
1
A
2
3
Рис.2.20.б - Плоское движение тела
(2.28)

44.

Эти уравнения называются уравнениями
плоского движения.
Точка А, движение которой задается, называется
полюсом.
Характеристиками плоского движения тела в
целом являются: скорость и ускорение полюса, а
также угловая скорость и угловое ускорение
тела ,
причем первые две характеристики зависят от
выбора полюса, а угловая скорость и угловое
ускорение не зависят.

45.

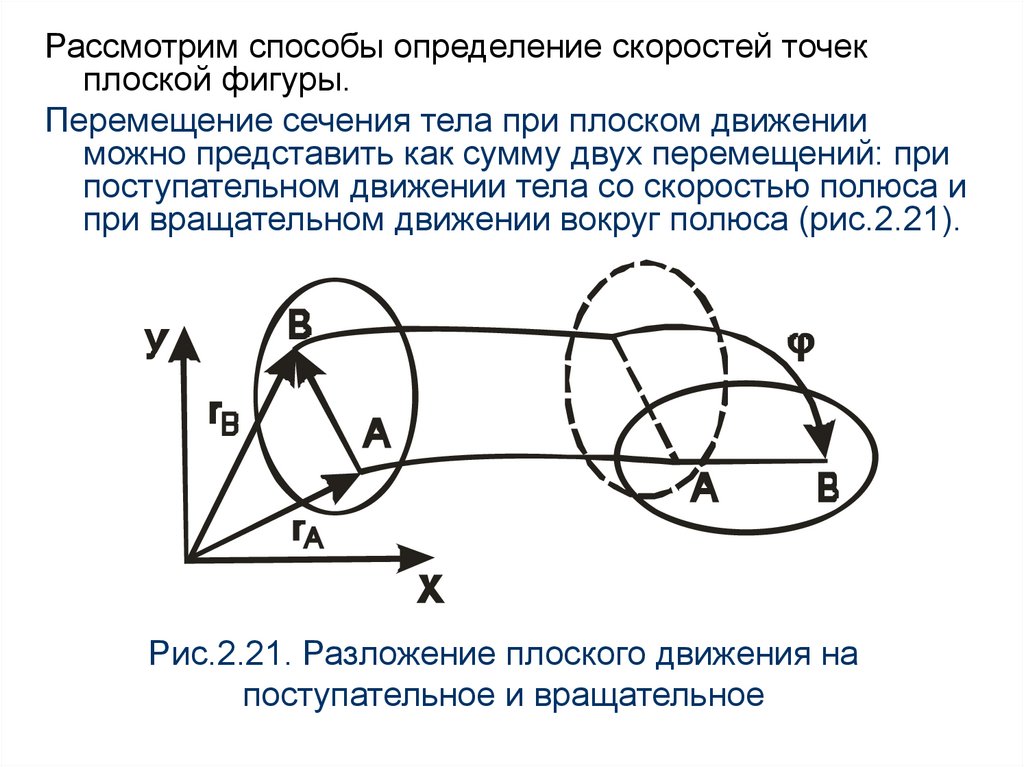
Рассмотрим способы определение скоростей точек
плоской фигуры.
Перемещение сечения тела при плоском движении
можно представить как сумму двух перемещений: при
поступательном движении тела со скоростью полюса и
при вращательном движении вокруг полюса (рис.2.21).
Рис.2.21. Разложение плоского движения на
поступательное и вращательное

46.

Из рисунка видно, что
rB rA AB
Продифференцируем это выражение по времени
drB drA dAB
dt
dt
dt
откуда:
v V V
B
A
ВА
(2.29)

47.

Следовательно,
скорость произвольной точки плоской фигуры
равна геометрической сумме скорости
полюса и скорости данной точки
относительно полюса.
Величина скорости точки В относительно полюса
А - равна произведению угловой скорости тела
на длину отрезка АВ,
направление скорости - перпендикулярно отрезку
АВ в сторону угловой скорости (рис 2.22).

48.

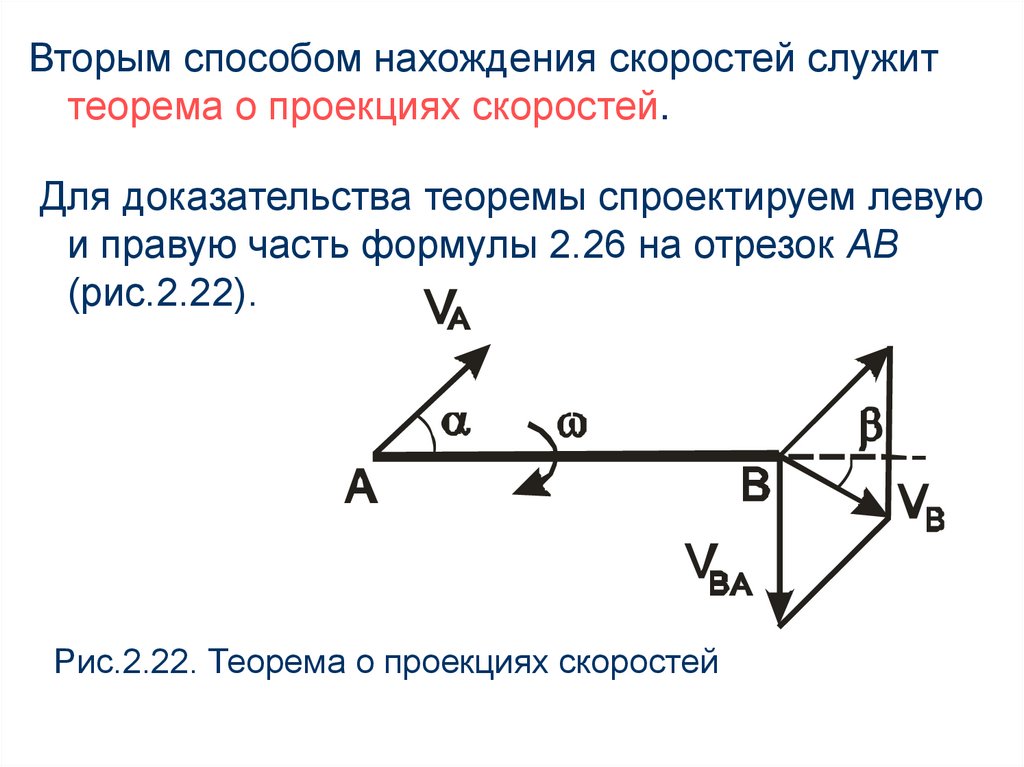
Вторым способом нахождения скоростей служит
теорема о проекциях скоростей.
Для доказательства теоремы спроектируем левую
и правую часть формулы 2.26 на отрезок АВ
(рис.2.22).
Рис.2.22. Теорема о проекциях скоростей

49.

V BA перпендикулярен
Поскольку вектор
отрезку АВ, то проекция его равна нулю,
поэтому имеем
VB cos VA cos
(2.30)
то есть проекции скоростей двух точек одного
твердого тела на отрезок, соединяющий их,
равны.
Пользуясь формулой (2.30) можно найти
величину скорости одной точки, если известно ее
направление и вектор скорости другой точки.

50.

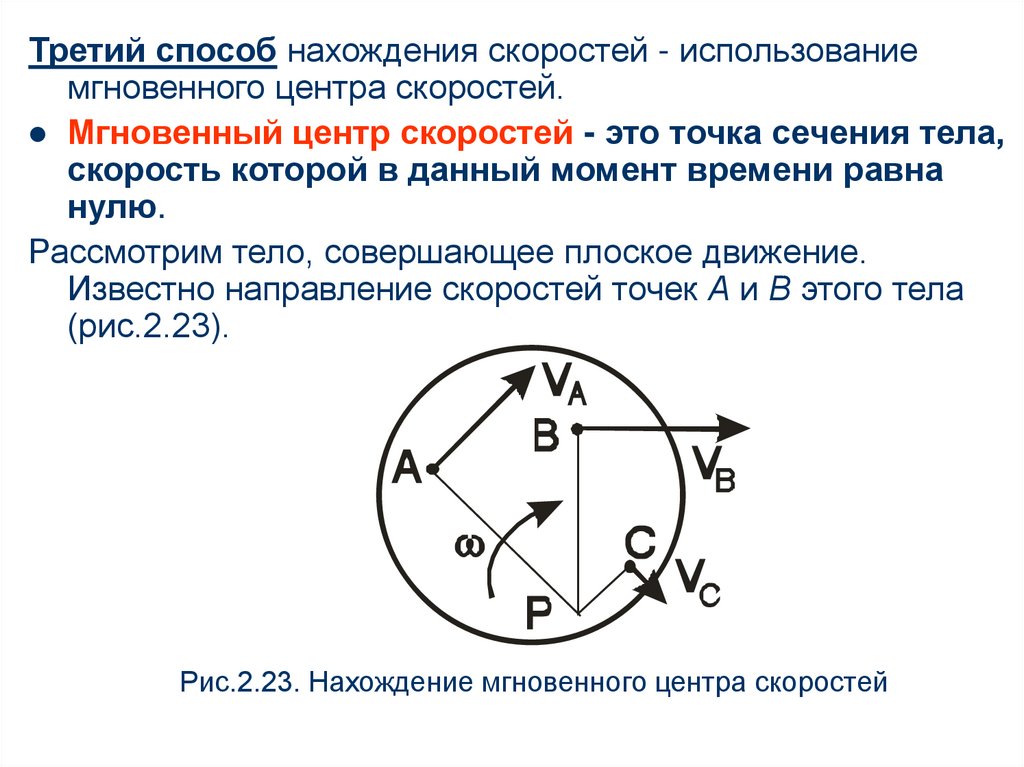
Третий способ нахождения скоростей - использование
мгновенного центра скоростей.
Мгновенный центр скоростей - это точка сечения тела,
скорость которой в данный момент времени равна
нулю.
Рассмотрим тело, совершающее плоское движение.
Известно направление скоростей точек А и В этого тела
(рис.2.23).
Рис.2.23. Нахождение мгновенного центра скоростей

51.

Восстановим перпендикуляры к направлениям
скоростей.
Покажем, что скорость точки Р пересечения
перпендикуляров равна нулю.
В самом деле, если она не равна нулю, то
согласно теореме о проекциях она должна быть
одновременно перпендикулярна отрезкам АР и
ВР, что невозможно, то есть точка Р мгновенный центр скоростей.
Принимая точку Р за полюс, скорость точки А
можно найти как
v v v
A
P
AP

52.

0
Поскольку v
, то скорость точки А можно
p
найти как скорость при
движении вокруг полюса
v v AP
A
вращательном
(2.31)
AP
Аналогично скорость любой точки плоской фигуры
равна произведению угловой скорости тела на
расстояние от этой точки до мгновенного центра
скоростей,
вектор скорости направлен перпендикулярно
отрезку, соединяющему данную точку с
мгновенным центром скоростей, в сторону
вращения тела.

53.

Таким образом, плоское движение можно
представить как сумму мгновенных
вращательных движений вокруг осей,
проходящих через мгновенные центры
скоростей.
Из формулы (2.31) следует, что угловая скорость
тела равна отношению скорости любой точки к
расстоянию от этой точки до мгновенного центра
скоростей
V A V B VC
AP BP CP

54. Итак, мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных из двух произвольных точек

тела, к скоростям этих
точек.
В некоторых случаях положение
мгновенного центра скоростей можно найти
без дополнительных построений. Так, при
качении колеса по неподвижной плоскости
без скольжения мгновенный центр будет
находиться в точке касания колеса с
опорной поверхностью (поскольку скорость
точек соприкосновения при качении без
скольжения одинакова, а скорость точек
неподвижной поверхности равна нулю).

55.

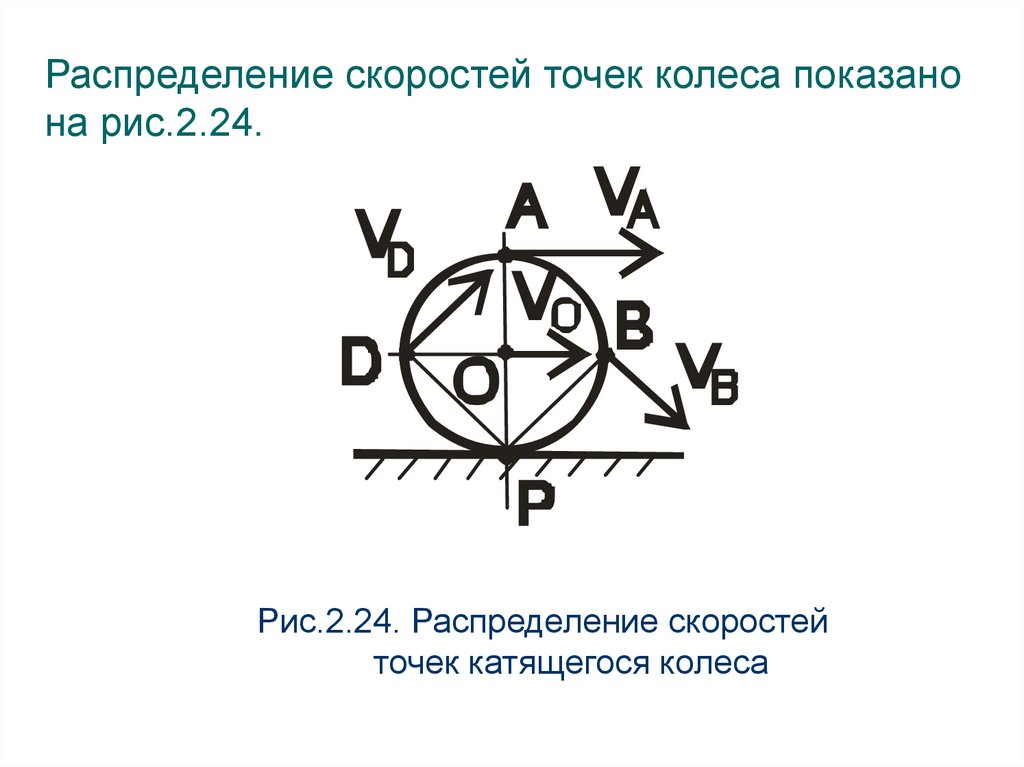
Распределение скоростей точек колеса показано
на рис.2.24.
Рис.2.24. Распределение скоростей
точек катящегося колеса

56.

Пример.
Кривошип ОА кривошипно-ползунного механизма
вращается равномерно с угловой скоростью 10
рад/с. Длина кривошипа ОА=0,2 м, длина шатуна
АВ=0,5 м. Определить угловую скорость шатуна
АВ и скорость его средней точки С при
горизонтальном (φ=0) и вертикальном (φ=π/2)
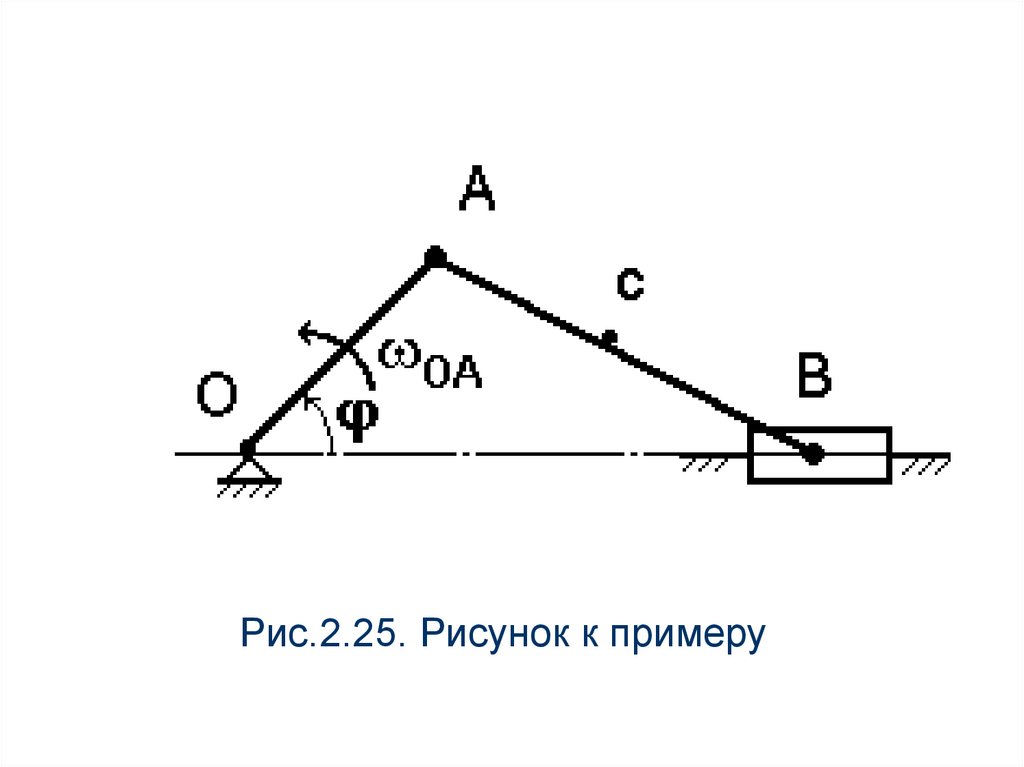
положениях кривошипа (рис.2.25).

57.

Рис.2.25. Рисунок к примеру

58.

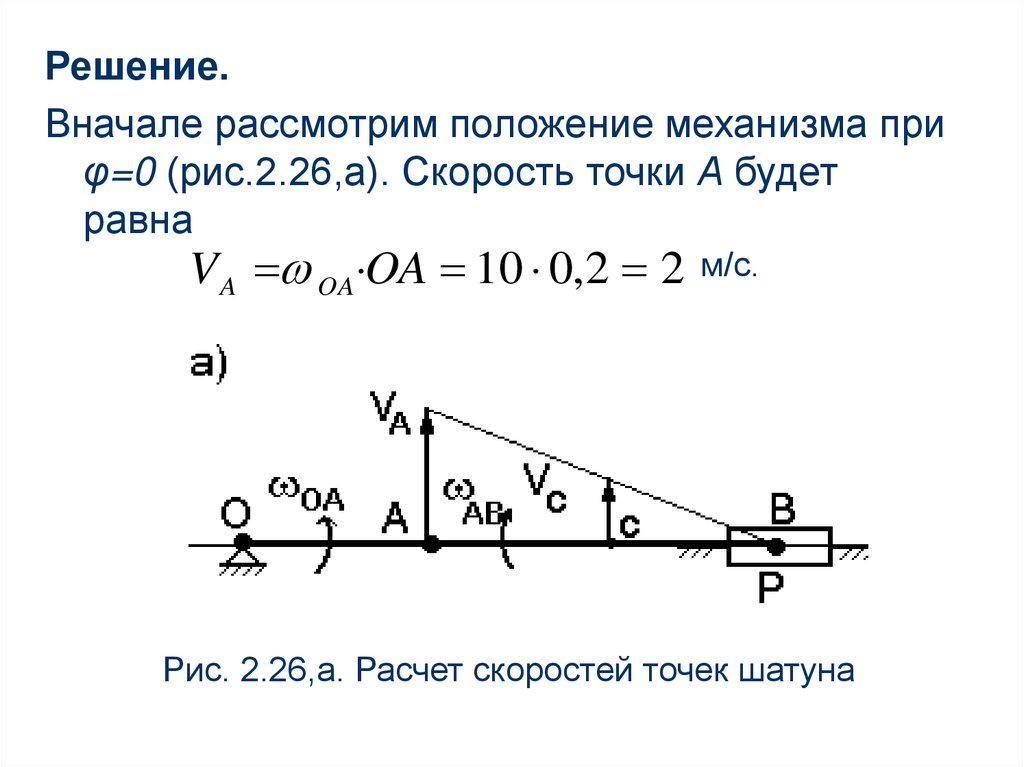
Решение.
Вначале рассмотрим положение механизма при
φ=0 (рис.2.26,а). Скорость точки А будет
равна
V A OA OA 10 0,2 2 м/с.
Рис. 2.26,а. Расчет скоростей точек шатуна

59.

Скорость точки А направлена перпендикулярно
кривошипу в сторону угловой скорости,
а скорость точки В может быть направлена по
горизонтальным направляющим.
Следовательно, если провести перпендикуляры к
скоростям точек А и В, то они пересекутся в точке
В и в ней будет находиться мгновенный центр
скоростей звена АВ.
Данное положение соответствует крайне правой
“мертвой“ точке ползуна.

60.

Угловая скорость звена АВ будет равна
AB VA AP 2 0,5 4 рад/с,
а скорость точки С -
VC AB CP 4 0,25 1 м/с

61.

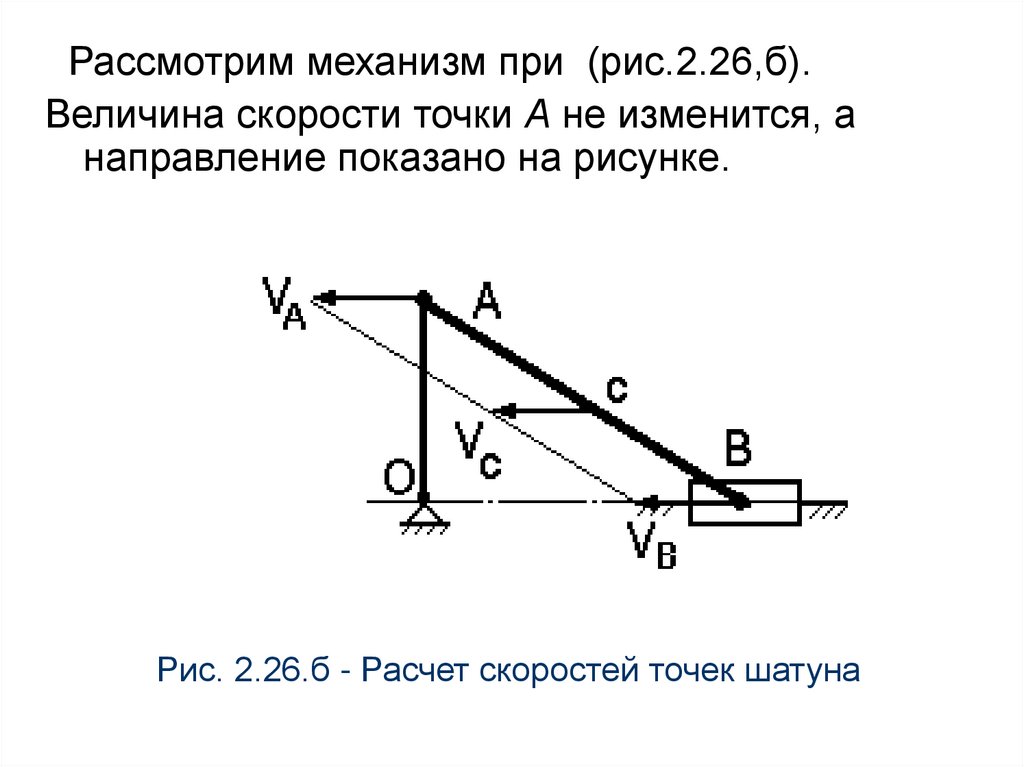
Рассмотрим механизм при (рис.2.26,б).
Величина скорости точки А не изменится, а
направление показано на рисунке.
Рис. 2.26.б - Расчет скоростей точек шатуна

62.

Поскольку вектора скоростей точек А и В
параллельны, то и перпендикуляры к скоростям
также будут параллельны, то есть точка
пересечения их находится в бесконечности.
Из этого следует, что угловая скорость шатуна АВ
в данном положении будет равна нулю,
то есть скорости всех точек шатуна будут
одинаковы: VC=VA=VB.
При помощи полученных формул можно делать
кинематический расчет планетарных и
дифференциальных передач.

63.

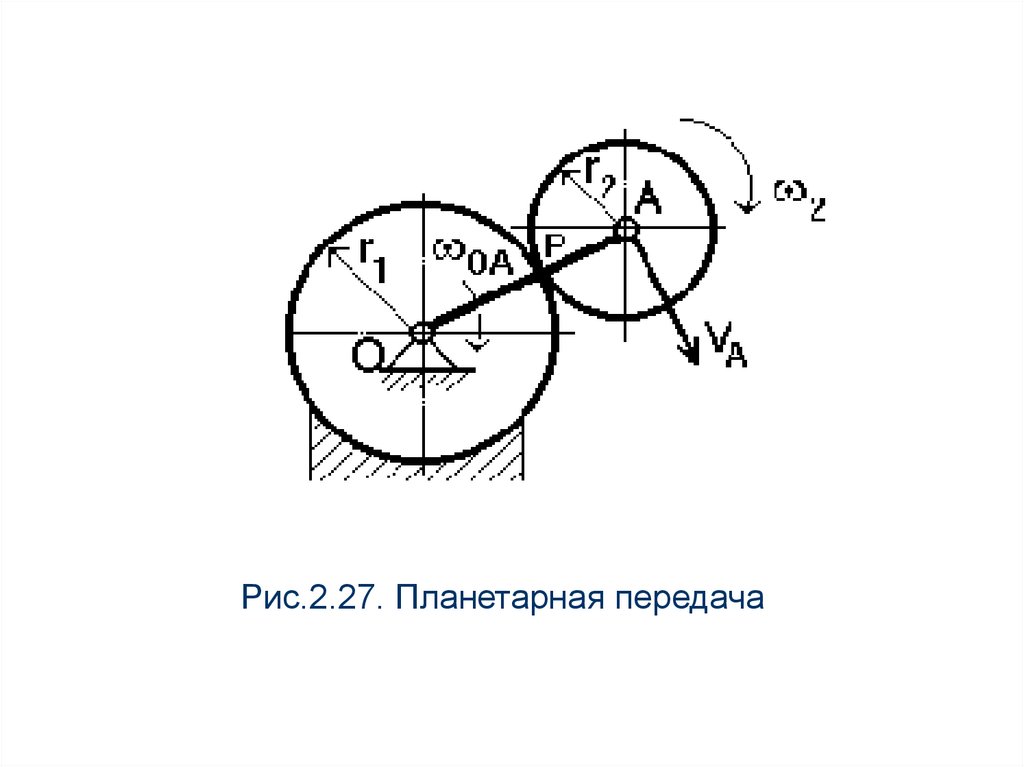
Пример.
Кривошип ОА планетарной передачи вращается с
постоянной угловой скоростью 20 рад/с.
Определить угловую скорость подвижного
колеса 2, если радиус неподвижного колеса 1
r1=10 см, а подвижного r2=5 см (рис.2.27).

64.

Рис.2.27. Планетарная передача

65.

Решение.
Найдем скорость точки А, находящейся на конце
кривошипа
V A OA OA OA (r1 r2 ) 20 (0,1 0,05) 3 м/с.
Мгновенный центр скоростей подвижного колеса
находится в точке касания с неподвижным,
поэтому угловая скорость подвижного колеса
будет равна
2 VA
AP V A / r2 3 / 0,05 60 рад/с.

66. 2.3.Сложное движение точки 2.3.1. Основные определения.

Сложным называется движение точки, которое
рассматривается относительно двух систем
отсчета – подвижной и неподвижной.
В некоторых случаях это значительно облегчает
решение задач кинематики.
В каждой системе отсчета движение будет
выглядеть по-разному.

67.

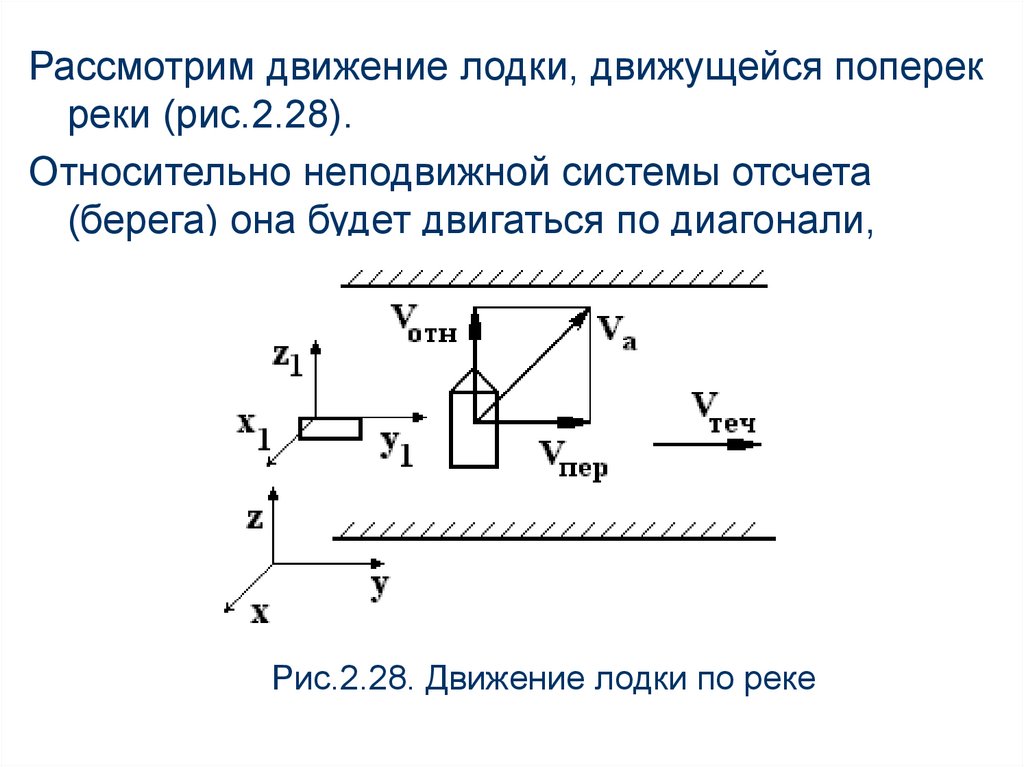
Рассмотрим движение лодки, движущейся поперек
реки (рис.2.28).
Относительно неподвижной системы отсчета
(берега) она будет двигаться по диагонали,
Рис.2.28. Движение лодки по реке

68.

а если рассматривать движение относительно
системы отсчета, связанной с водой, то
перпендикулярно берегу это движение увидит
человек, сидящий на бревне, которое плывет
по течению.

69.

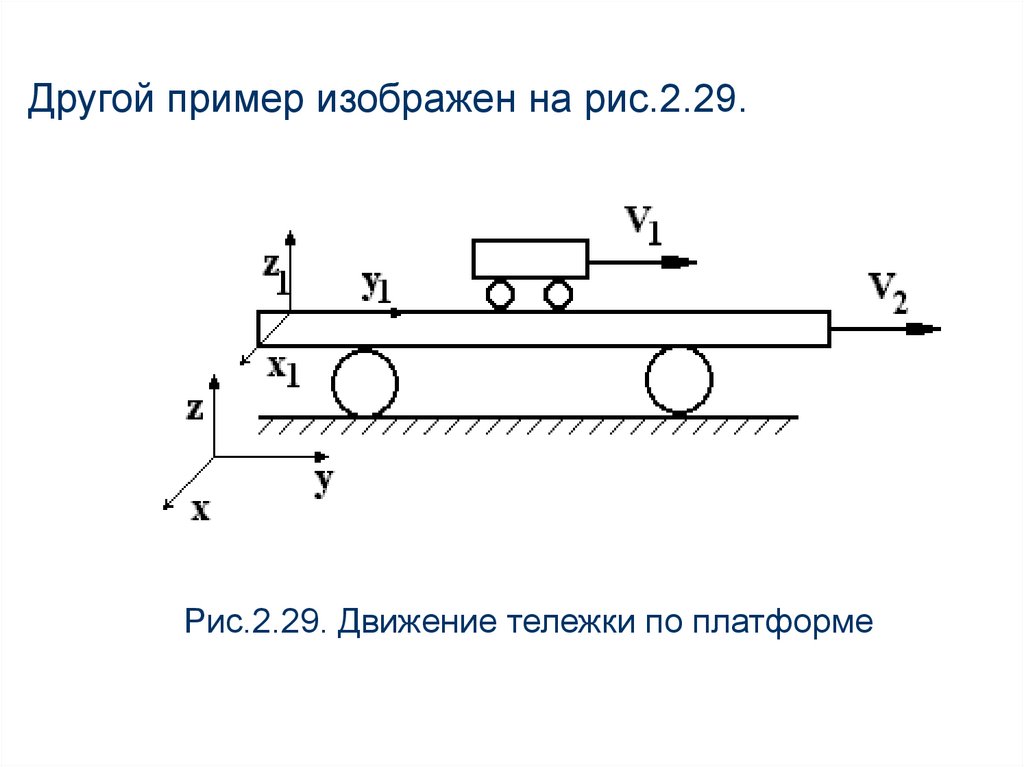
Другой пример изображен на рис.2.29.
Рис.2.29. Движение тележки по платформе

70.

Тележка движется по платформе. Если
рассматривать движение тележки
относительно подвижной системы отсчета,
связанной с платформой, то ее скорость
будет равна V1,
а относительно неподвижной системы,
связанной с рельсами, - V1+V2.

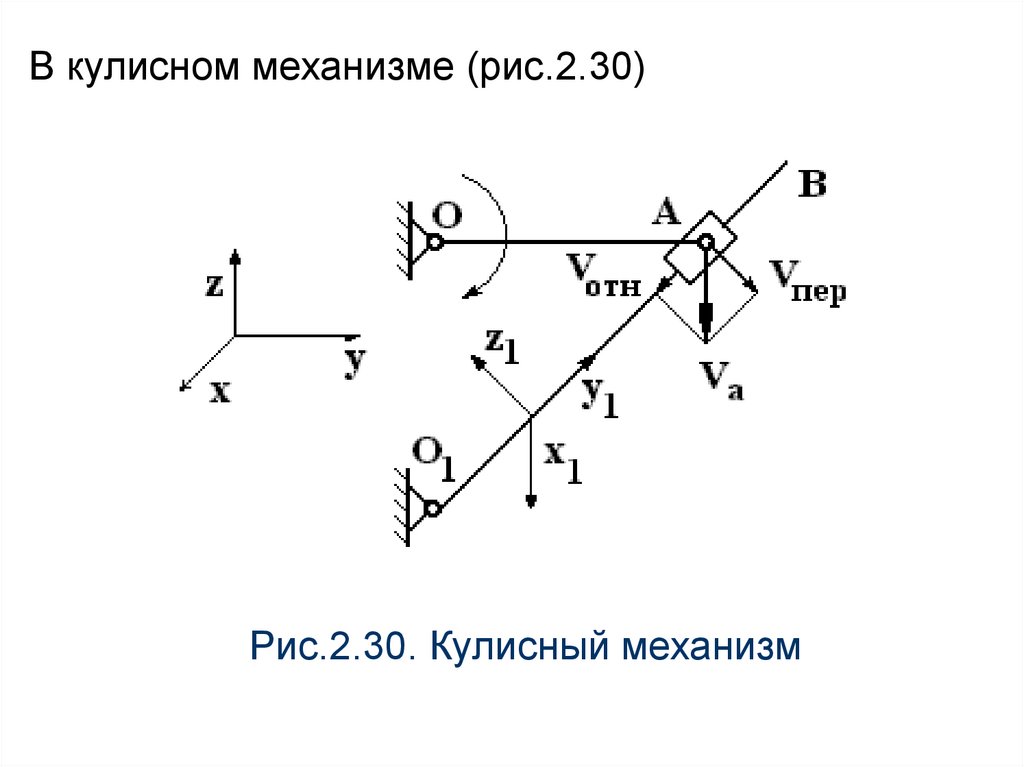
71.

В кулисном механизме (рис.2.30)
Рис.2.30. Кулисный механизм

72.

точка А относительно корпуса будет двигаться по
окружности радиуса ОА, а относительно
кулисы О1В - по прямой, то есть неподвижная
система отсчета XYZ связана с корпусом, а
подвижная – X1 Y1 Z1 с кулисой O1В .
Движение точки относительно неподвижной
системы отсчета называется абсолютным, а ее
скорость в этом движении – абсолютной
скоростью
Va

73.

Движение точки относительно подвижной
системы отсчета называется относительным,
а ее скорость в этом движении –
относительной скоростью - V .
отн
Движение подвижной системы со всеми
жестко связанными с ней точками
пространства относительно неподвижной
системы отсчета называется переносным, а
скорость точки подвижной системы,
совпадающей с данной точкой – переносной
скоростью - V .
пер

74.

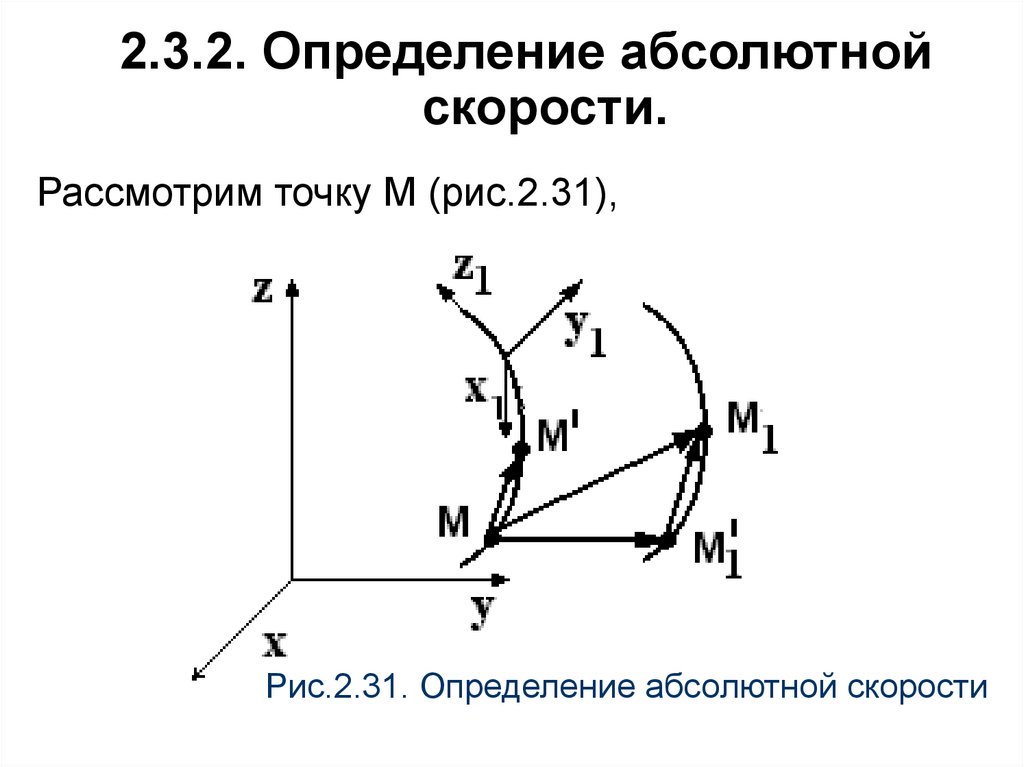
2.3.2. Определение абсолютной
скорости.
Рассмотрим точку М (рис.2.31),
Рис.2.31. Определение абсолютной скорости

75.

Рассмотрим точку М, движущуюся по кривой
АВ, которая, в свою очередь, движется
относительно неподвижной системы
отсчета (рис.2.31).
Если бы кривая не двигалась, то за время
Δt точка перешла бы в положение M/, так
как кривая движется, то она перейдет в
положение М1. Вектор
ММ 1 ММ 1 М 1 М 1
равен абсолютному перемещению точки.

76.

Разделим на Δt и перейдем к пределу
MM 1
MM 1
M 1 M 1
lim
lim
lim
t 0 t
t 0 t
t 0
t
Отсюда
Va Vпер Vотн
(2.32)
Таким образом, абсолютная скорость равна
геометрической сумме переносной и
относительной скоростей.

77.

Геометрическая интерпретация
формулы (2.32) изображена на рис.2.32.
Рис.2.32. Сложение скоростей
По теореме косинусов
2
2
Va Vпер
Vотн
2VперVотн cos(180 )
или
2
2
Va Vпер
Vотн
2VперVотн cos
(2.33)

78.

По формуле (2.33) можно найти модуль скорости
при различных углах между относительной и
переносной скоростями (рис.2.35).
При
0
Va Vпер Vотн
Рис.2.35. Частные случаи сложения скоростей

79.

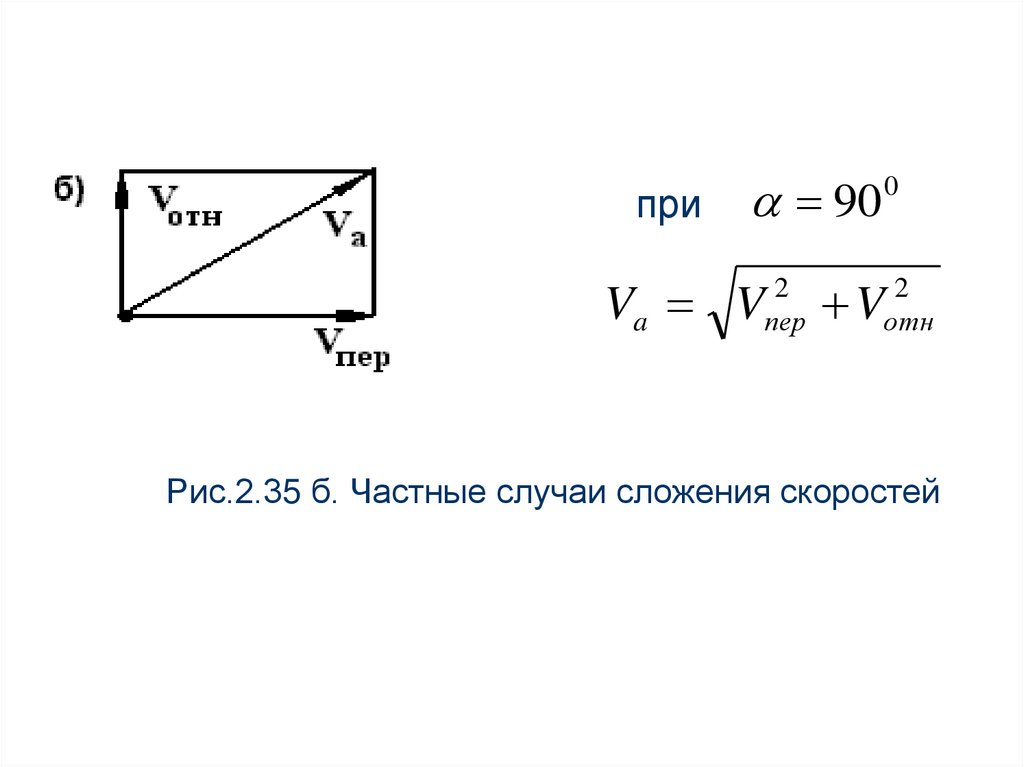
при
90
Va V
2
пер
0
V
2
отн
Рис.2.35 б. Частные случаи сложения скоростей

80.

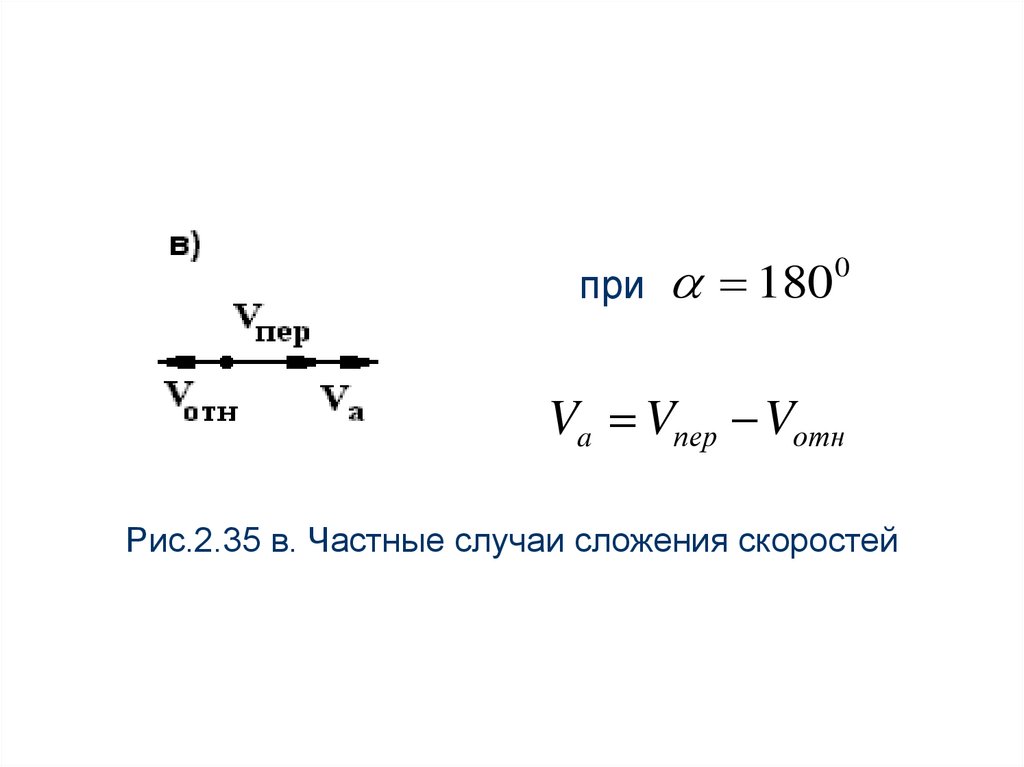
при 180
0
Va Vпер Vотн
Рис.2.35 в. Частные случаи сложения скоростей

81.

2.3.3. Определение абсолютного
ускорения.
Для определения абсолютного ускорения
используется теорема Кориолиса: абсолютное
ускорение точки равно геометрической
сумме переносного ускорения,
относительного ускорения и ускорения
Кориолиса
а а а пер а отн. а к
(2.34)
Формула (2.34) получена путем дифференцирования
(2.32) по времени.

82.

Переносное ускорение характеризует
изменение переносной скорости в переносном
движении,
относительное ускорение характеризует
изменение относительной скорости в
относительном движении,
а ускорение Кориолиса- изменение переносной
скорости в относительном движении и
относительной – в переносном.

83.

Ускорение Кориолиса определяется по формуле
ак 2 пер Vотн
то есть равно удвоенному векторному
произведению вектора переносной угловой
скорости на вектор относительной скорости.
Вектор переносной угловой скорости
направляется по оси вращения так, чтобы глядя
с его конца поворот тела был виден против
часовой стрелки.

84.

Модуль ускорения Кориолиса находится как
модуль векторного произведения
ак 2 перVотн sin
(2.36)
- угол между векторами пер и Vотн
Направление ускорения Кориолиса находится, как
направление векторного произведения, то есть
перпендикулярно
проходящей
плоскости,
через вектора пер и Vотн так, чтобы, глядя
с его конца, поворот вектора на наименьший
угол был виден против часовой стрелки.

85.

Заметим, что если переносное и относительное движение
будут происходить в одной плоскости, то есть угол α=90о ,
для определения направления ускорения Кориолиса надо
вектор относительной скорости повернуть на 90о в сторону
вращения.
Из формулы (2.36) следует, что ускорение Кориолиса
равно нулю в трех случаях.
1.
=0, то есть если переносное движение
поступательное.
2.
=0, то есть при мгновенной остановке точки в
относительном движении.
3.
=0, то есть когда вектора
и
параллельны.

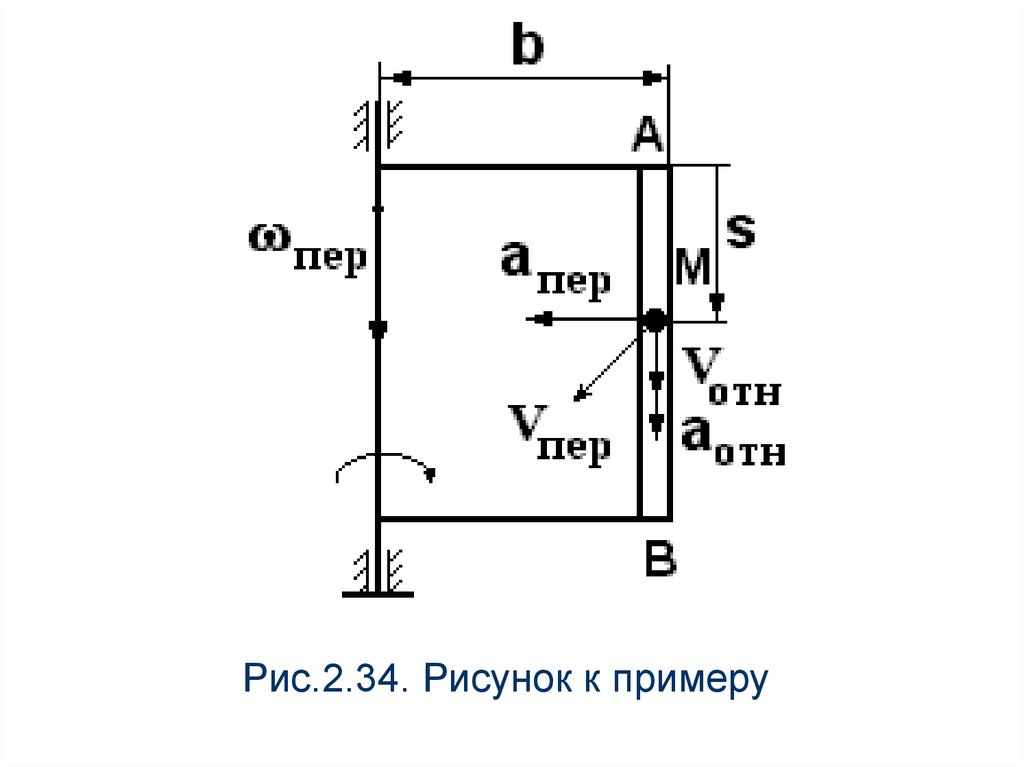
86.

Пример.
Пластина со стороной b=20 см вращается с
постоянной угловой скоростью 2 рад/с
(рис.2.34). По стороне АВ движется точка М
по закону S=5t2 см. Определить абсолютную
скорость и абсолютное ускорение точки М в
момент времени t=2 c.

87.

Рис.2.34. Рисунок к примеру

88.

Решение.
Подвижную систему отсчета связываем с
пластиной, поэтому относительным будет
движение точки по пластине. Для того, чтобы
найти относительную скорость, надо остановить
переносное движение.
Относительная скорость
Vотн S 10t
при t=2 c Vотн=20 см/с.

89.

Относительное ускорение
аотн S 10
см/с2
Для того, чтобы определить переносную скорость, надо
остановить относительное движение, то есть считать,
что точка закреплена на пластине
Vпер b =40 см/с
Переносное ускорение
a пер 0 так как пер= const).
n
апер апер
2b =40 см/с2

90.

Для сложения скоростей используем формулу
(2.32). Учитывая, что векторы относительной и
переносной скоростей перпендикулярны друг
другу, абсолютную скорость найдем по формуле
2
2
Va Vпер
Vотн
402 202 44,7 см/с
Для определения абсолютного ускорения
используем теорему Кориолиса
а а а пер а отн а к
Вектор переносной скорости направлен по оси вращения
пластины, поэтому он будет параллелен вектору
относительной скорости, следовательно, ускорение
Кориолиса будет равно нулю. Тогда

91.

аа апер аотн
Поскольку вектора переносного и относительного
ускорения перпендикулярны, то
2
2
аa апер
аотн
802 102 80,6 см/с2.

92. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Какие существуют способы для задания
движения точки?
2. Как находятся скорость и ускорение точки при
векторном способе задания движения?
3. Как находятся скорость и ускорение точки при
координатном способе задания движения?
4. Как находятся скорость и ускорение точки при
естественном способе задания движения?
5. Как направляются естественные оси
координат?
6. Как находится скорость и перемещение точки
при равнопеременном движении?

93.

7. Зависимости между скоростями и
ускорениями точек при поступательном
движении тела.
8. Как задается вращательное движение тела?
9. Как находится средняя угловая скорость?
10. Как находится мгновенная угловая
скорость?
11. Как находится мгновенное угловое
ускорение?
12. В каких единицах измеряются угловая
скорость и угловое ускорение?
13. Как определяется скорость точки,
находящейся на вращающемся теле?

94.

14. Как определяется ускорение точки, находящейся на
вращающемся теле?
15. Как задается плоско-параллельное движение тела?
16. Какая точка называется мгновенным центром
скоростей?
17. Как находится скорость точки при помощи мгновенного
центра скоростей?
18. Как формулируется теорема о проекциях скоростей?
19. Где находится мгновенный центр скоростей при
качении тела по неподвижной поверхности?
20. Какое движение называется сложным?
21. Как находится абсолютная скорость точки?

95.

22. Как находится абсолютное ускорение точки при
поступательном переносном движении?
23. Как находится абсолютное ускорение точки при
вращательном переносном движении?
24. В каких случаях ускорение Кориолиса равно нулю?