Логическое программирование. Лекция 5

1. Лекция №5 Логическое программирование

2. План лекции

• Синтаксис и семантика логической
программы. Декларативная и
процедурная семантика Пролога.
• Алгоритм работы интерпретатора
логической программы
• Дерево поиска решений
• Механизм отката

3. Синтаксис и семантика логической программы

Логическая программа представляет собой
базу знаний, состоящую из предложений.
Каждое предложение имеет синтаксис
A :- B1, B2, … , Bn.
где A, B1, B2, … , Bn – предикаты.

4. Синтаксис и семантика логической программы

Предикат – это выражение вида
pred (term1,...,termm)
где pred – имя предиката (предикатный
символ),
term1,...,termm - термы.
Декларативный смысл предиката и термов:
предикат задает отношение между
объектами, задаваемыми термами
term1,...,termm .

5. Синтаксис и семантика логической программы

Терм – это константа, переменная или составной
терм.
Константа – число или атом.
Атом – цепочка символов, начинается с маленькой
буквы. Указывает на конкретный объект.
Переменная – цепочка символов, начинается с большой
буквы. Указывает на неопределенный объект.
Составной терм – выражение вида:
func (term1,...,termm)
где func – имя функции (функциональный символ),
term1,...,termm - термы. Позволяет реализовать понятие
функции.

6. Декларативная и процедурная семантика логической программы

Логическая программа обладает как декларативной, так
и процедурной семантикой.
Правило в программе на языке Prolog вида
A :- B1 , B2 , … , Bn .
можно трактовать двояко:
1) как логическое высказывание (хорновский дизъюнкт)
B1 B2 … Bn A (декларация)
2) как определение процедуры A, утверждающее, что
для выполнения A надо последовательно выполнить
подпрограммы B1 , B2 , … , Bn .
Наличие процедурной семантики – отличие логического
программирования от логики предикатов.

7. Обратный вывод в логическом программировании

Цель : g
Правило:
a:- b1,…, bm.
___________________________________
Применение обобщенного правила Modus Ponens
состоит из следующих шагов:
1) Унификация цели g и заголовка правила a
= Unify(g, a)
2) Формируем новую цель - b1’ ,…, bm’
где
b1’ = Subst( , b1), …, bm’ = Subst( , bm)
К полученным целям вновь применяется Modus Ponens,
и т.д., пока в итоге все цели не подтвердятся фактами.

8. Метод входной линейной резолюции в логическом программировании

Цель : g
Правило: a:- b1,…, bm.
(1 дизъюнкт
¬g)
(2 дизъюнкт ¬ b1 … ¬ b1 a)
Применение правила резолюции состоит из двух шагов:
1) Унификация цели g и заголовка правила a
= Unify(g, a). В результате получаем контрарную пару
(Subst( , ¬g), Subst( ,a))
2) Применяем правило резолюций. В результате получаем
новую конъюнктивную цель
¬ b1’ … ¬ bm’= ¬ (b1’ … ¬ bm’),
где b1’ = Subst( , b1), …, bm’ = Subst( , bm)
К полученным целям вновь применяется правило
резолюций и т.д., пока все цели не подтвердятся
фактами.

9. Алгоритм работы интерпретатора ЛП

Вводится понятие текущей резольвенты R - множество
целей, генерируемых в процессе логического вывода.
1) Первоначально в резольвенту R заносится исходная
цель: R={ g }. Пусть на очередном шаге получена текущая
резольвента R={ g1,…, gn }.
2) В программе находится предложение a:- b1,…, bm. ,
такое что Unify(a,g1)= 1. В этом случае формируется
новая резольвента
R={ b1',…, bm', g2',…, gn' },
где bi'=Subst( 1, bi),
gj'=Subst( 1, gj).
Если правила для доказательства текущей цели не
найдено, то выход из программы (неуспех).
3) Процесс продолжается до тех пор, пока R .
R= - окончание работы (успешное доказательство цели).
Итоговая подстановка есть композиция = 1 2 3 …

10. Дерево поиска решений

1. Корнем дерева является исходная цель(исходная резольвента).
2. Вершинами дерева являются текущие цели (текущие
резольвенты), получающиеся в результате применения правила
резолюции, причем самая левая (снимаемая) подцель в каждой
вершине подчеркивается.
3. Ребро, ведущее из вершины дерева, соответствует успешной
унификации выделенной подцели с заголовком одного из
предложений программы. Рядом с ребром подписывается
подстановка, получающаяся в результате унификации.
4. Каждое ребро ведет к новой резольвенте, полученной в
результате одного применения правила резолюций.
5. Листья дерева соответствуют успешному вычислению цели,
если в результате получается пустая резольвента
6. Листья дерева являются безуспешными вершинами, если цель,
выделенная в вершине, не может быть доказана.
7. Количество решений цели определяется как количество
успешных вершин.

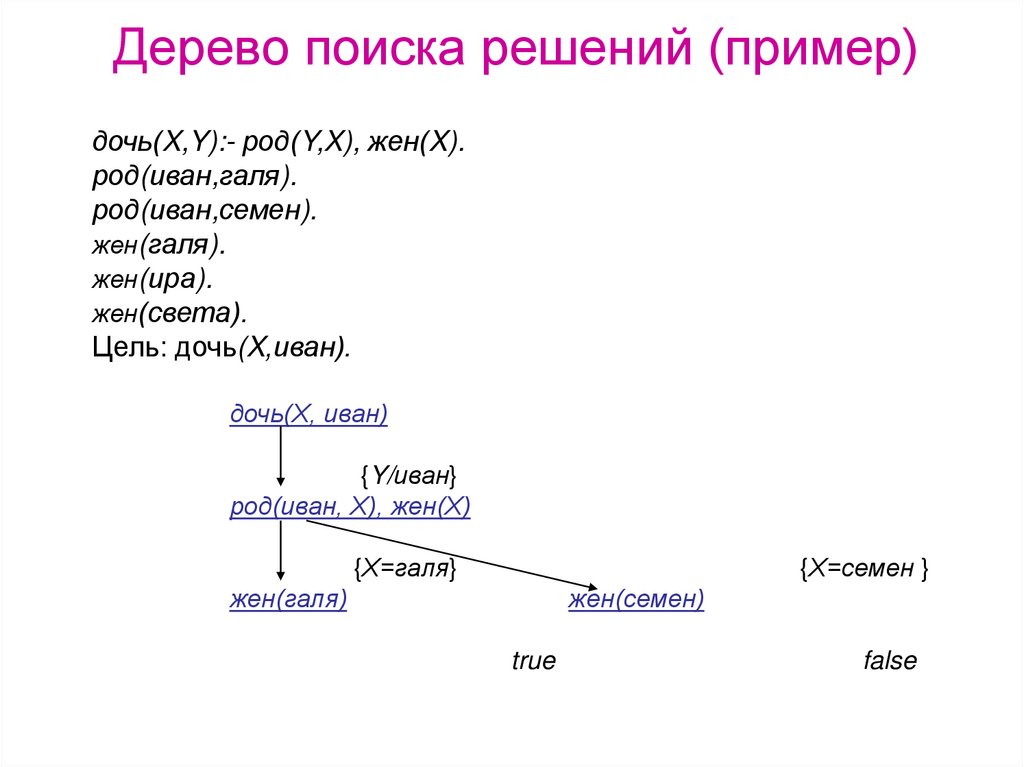
11. Дерево поиска решений (пример)

дочь(X,Y):- род(Y,X), жен(X).
род(иван,галя).
род(иван,семен).
жен(галя).
жен(ира).
жен(света).
Цель: дочь(X,иван).
дочь(Х, иван)
{Y/иван}
род(иван, Х), жен(Х)
{Х=галя}
{Х=семен }
жен(галя)
жен(семен)
true
false

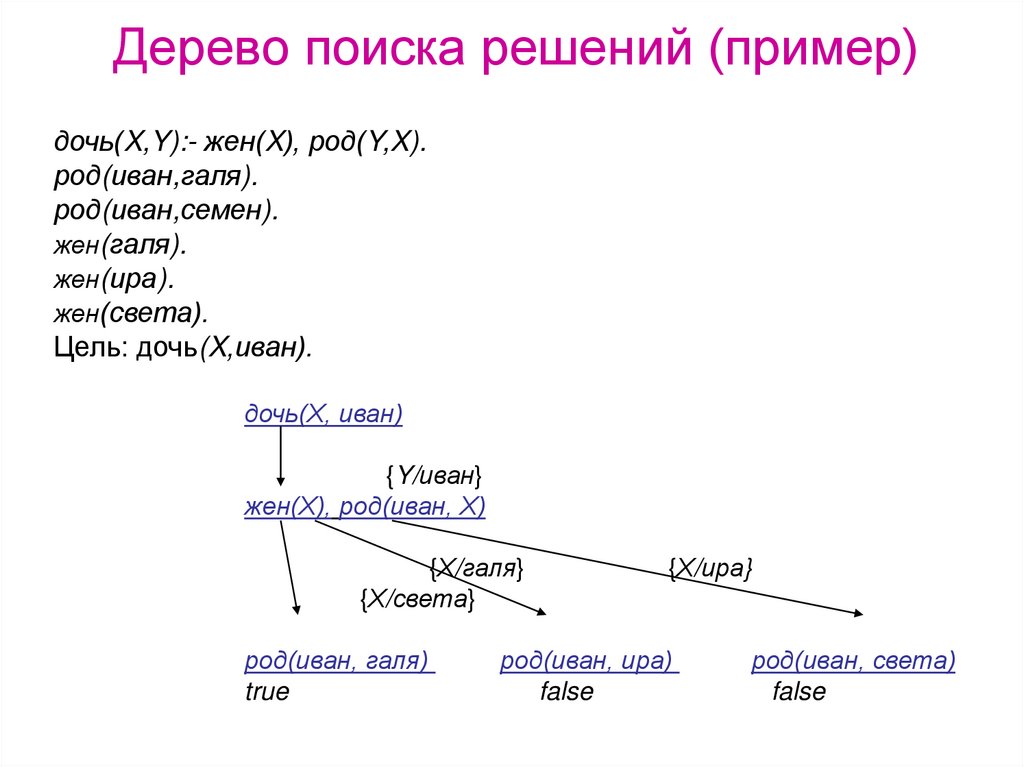
12. Дерево поиска решений (пример)

дочь(X,Y):- жен(X), род(Y,X).
род(иван,галя).
род(иван,семен).
жен(галя).
жен(ира).
жен(света).
Цель: дочь(X,иван).
дочь(Х, иван)
{Y/иван}
жен(Х), род(иван, Х)
{Х/галя}
{Х/света}
род(иван, галя)
true
{Х/ира}
род(иван, ира)
false
род(иван, света)
false

13. Логическая программа. Пример использования составных термов

parent(person("Bill", male), person("John", male)).
parent(person("Pam", female),person("Bill", male)).
parent(person("Pam", female),person("Jane", female)).
parent(person("Jane", female), person(("Sue", female)).
father(P,person(Name, male)) :- parent(P,person(Name, male)).
mother(P,person(Name,female)) :-parent(P,person(Name,female)).
grandFather(Person,TheGrandFather):parent(Person,ParentOfPerson),
father(ParentOfPerson,TheGrandFather).
grandMother(Person,TheGrandMother):parent(Person,ParentOfPerson),
mother(ParentOfPerson,TheGrandMother).

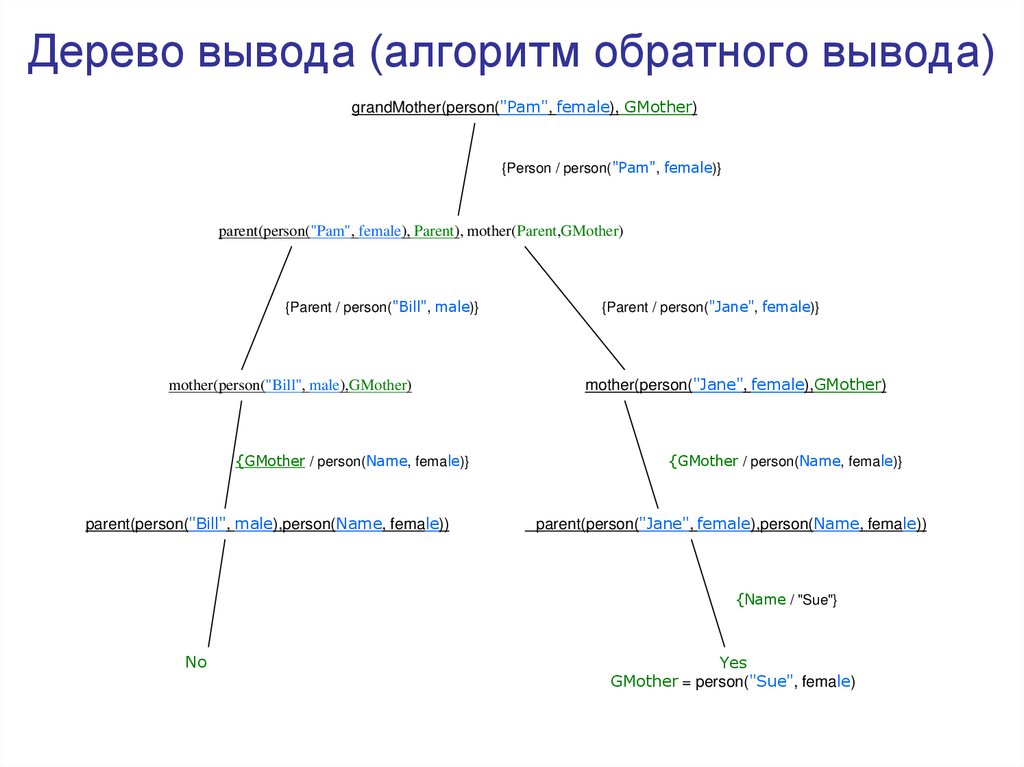
14. Дерево вывода (алгоритм обратного вывода)

grandMother(person("Pam", female), GMother)
{Person / person("Pam", female)}
parent(person("Pam", female), Parent), mother(Parent,GMother)
{Parent / person("Bill", male)}
mother(person("Bill", male),GMother)
{GMother / person(Name, female)}
parent(person("Bill", male),person(Name, female))
{Parent / person("Jane", female)}
mother(person("Jane", female),GMother)
{GMother / person(Name, female)}
parent(person("Jane", female),person(Name, female))
{Name / "Sue"}
No
Yes
GMother = person("Sue", female)

15. Управление порядком вычислений на Прологе

Отличия Пролога от теоретической модели
логического программирования:
1) Правила в Прологе просматриваются сверху
вниз, а в теоретической модели правила
выбираются произвольным образом.
2) Цели в теле правила (в резольвенте)
обрабатываются слева направо, в
теоретической модели цели выбираются
произвольным образом.
3) Механизм отката (бэктрекинг).

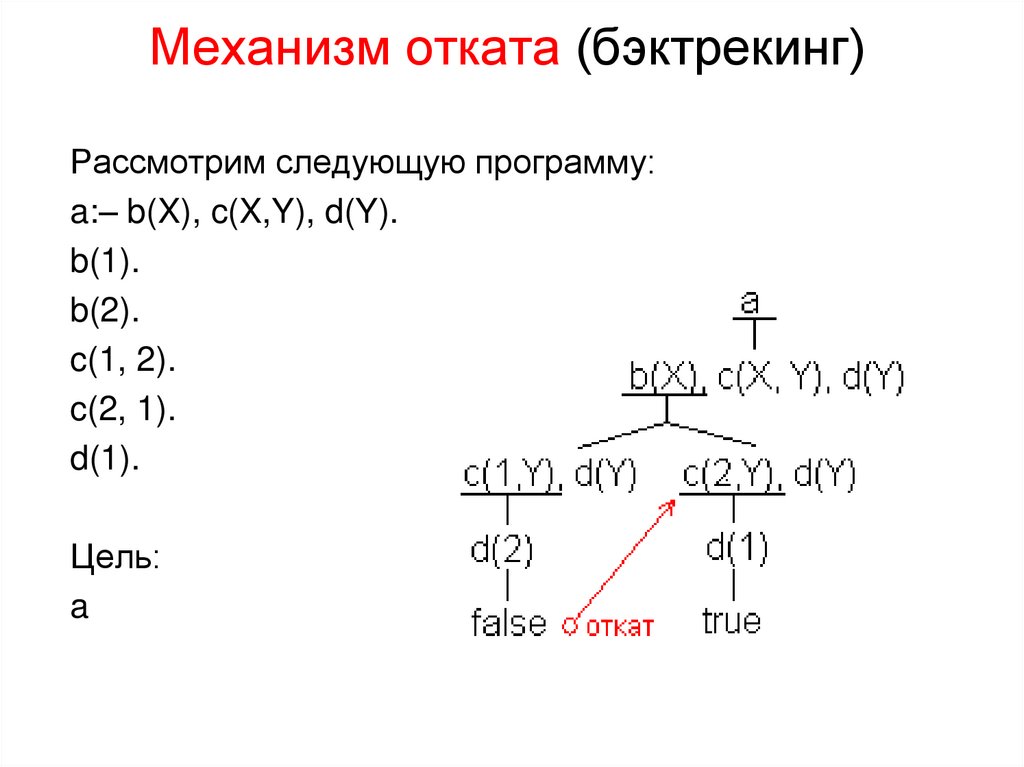
16. Механизм отката (бэктрекинг)

Рассмотрим следующую программу:
a:– b(X), c(X,Y), d(Y).
b(1).
b(2).
c(1, 2).
c(2, 1).
d(1).
Цель:
a

17. Механизм отката (бэктрекинг)

Детерминированная цель – цель, для доказательства
которой имеется только одна альтернатива.
Недетерминированная цель - цель, для доказательства
которой имеется более одной альтернативы
(недетерминированные цели соответствуют
разветвлениям на дереве поиска).
Откат – это возврат от точки неуспеха назад, к
ближайшей по дереву точке возврата
(недетерминированной подцели).
В процессе отката теряются все связывания
переменных, полученные между точкой возврата и
точкой неуспеха.

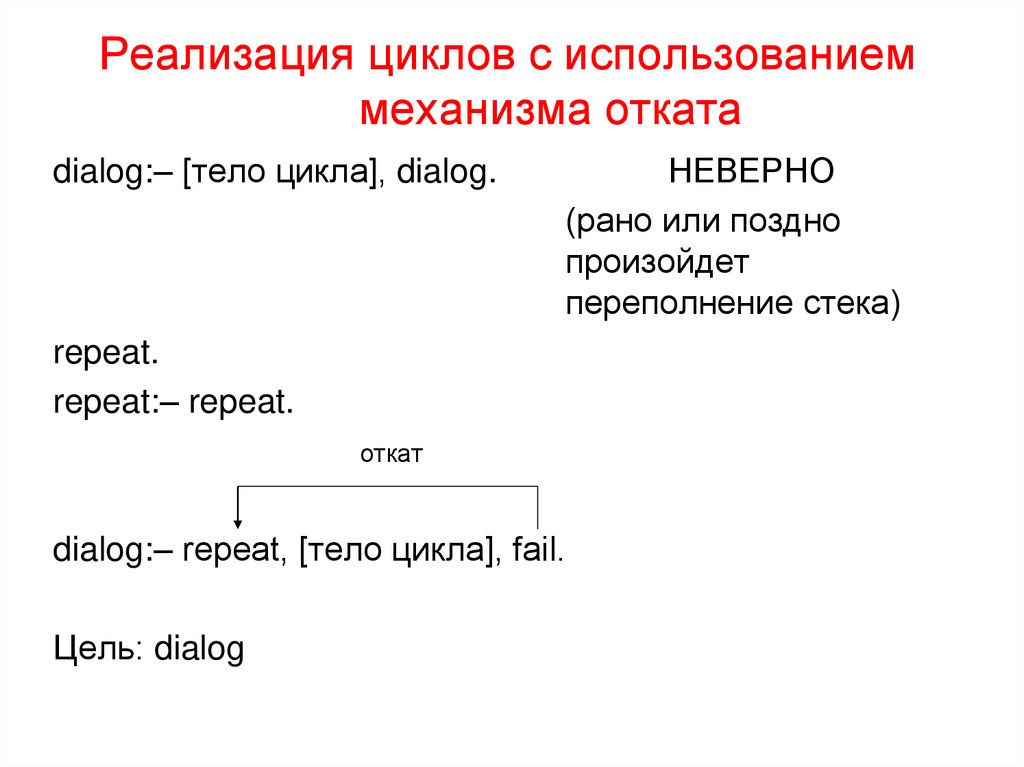
18. Реализация циклов с использованием механизма отката

dialog:– [тело цикла], dialog.
НЕВЕРНО
(рано или поздно
произойдет
переполнение стека)
repeat.
repeat:– repeat.
откат
dialog:– repeat, [тело цикла], fail.
Цель: dialog

19. Цикл со счетчиком с использованием механизма отката

dialog:– for(I, 1, N), [тело цикла], I>=N.
for(A, A, _).
for(I,A,B):– A<B, A1=A+1, for(I,A1,B).
Упражнение. Построить дерево поиска решений для
следующего правила:
dialog:– N=3, for(I, 1, N), write(I), I>=N.