Похожие презентации:
Решение задач несколькими способами. Равнобедренный треугольник
1. Не будем жалеть времени, или решение задачи несколькими способами
2.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
Способ 1
В прямоугольном
треугольнике BKC угол KСВ
равен 60°, тогда в
треугольнике NMC угол NMC
равен 30°. Значит, смежный с
углом NMC угол АМС имеет
градусную меру 150°.
М
3.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
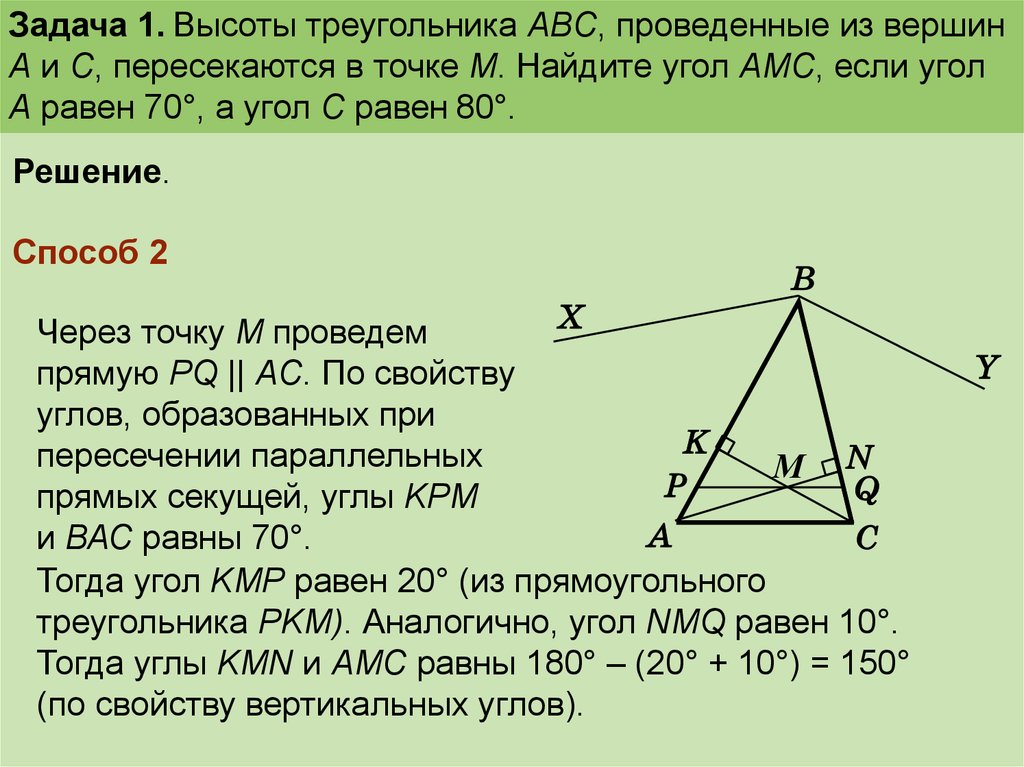
Способ 2
Через точку М проведем
прямую PQ || AC. По свойству
углов, образованных при
пересечении параллельных
М
прямых секущей, углы KРМ
и ВАС равны 70°.
Тогда угол KМР равен 20° (из прямоугольного
треугольника РKМ). Аналогично, угол NMQ равен 10°.
Тогда углы KMN и AMC равны 180° – (20° + 10°) = 150°
(по свойству вертикальных углов).
4.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
Способ 3
В четырехугольнике MKBN
угол KBM равен 30°, а углы
BKN и BNM равны 90°. Угол
KMN, вертикальный с
искомым углом AMC, равен
360° – 90° – 90° – 30° = 150°.
М
5.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
Способ 4
В прямоугольных
треугольниках АKС и ANC угол
KCA равен 90°– 70°= 20°,
угол NAC равен 90°– 80°= 10°,
тогда в треугольнике АМС
угол AMC равен
180° – (20° + 10°) = 150°.
М
6.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
Способ 5
В прямоугольных
треугольниках АNB и CKB
углы BAN и BCK равны 60°.
Тогда угол NAC будет равен
70°– 60°= 10°, угол KCA равен
80°– 60°= 20°. Тогда в
треугольнике АМС угол AMC
равен 180° – (20° + 10°) = 150°.
М
7.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
Способ 6
Углы со взаимно
перпендикулярными сторонами
равны, если они оба тупые или оба
острые. Если один из этих углов
острый, а другой тупой, то сумма их
градусных мер равна 180°.
Поэтому если угол B острый и
равен 30°, то угол AMC тупой и
равен 150°.
М
8.
Задача 1. Высоты треугольника ABC, проведенные из вершинА и С, пересекаются в точке М. Найдите угол АМС, если угол
А равен 70°, а угол C равен 80°.
Решение.
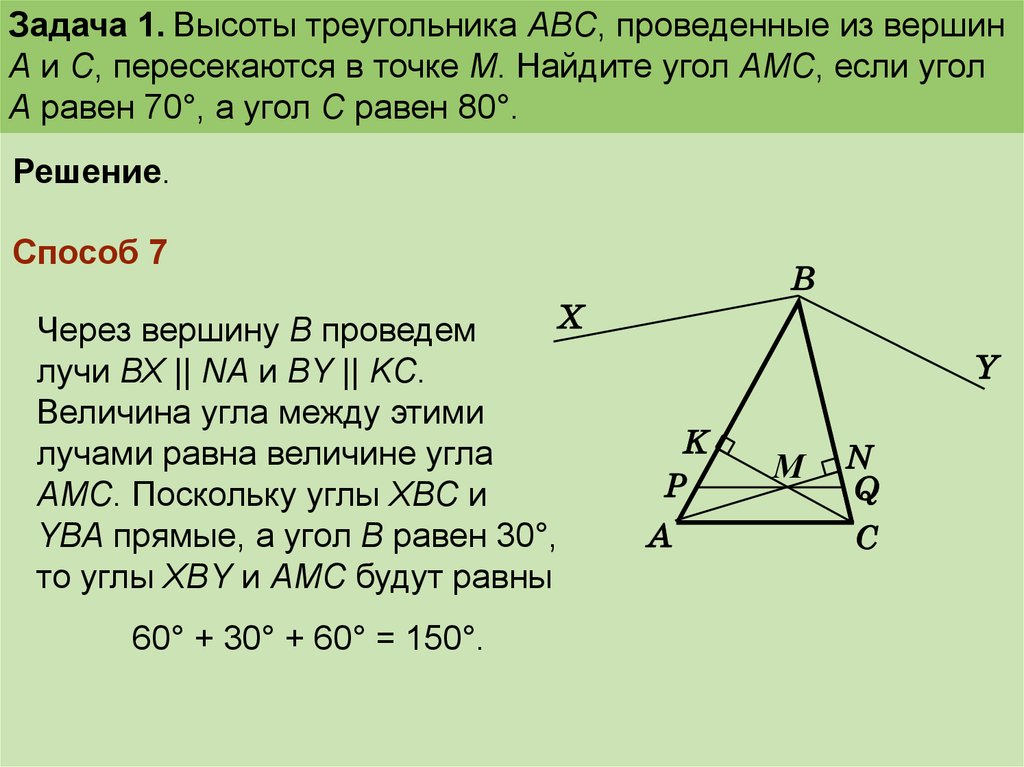
Способ 7
Через вершину В проведем
лучи ВХ || NA и ВY || KC.
Величина угла между этими
лучами равна величине угла
АМС. Поскольку углы ХВС и
YВА прямые, а угол B равен 30°,
то углы XBY и AMC будут равны
60° + 30° + 60° = 150°.
М
9.
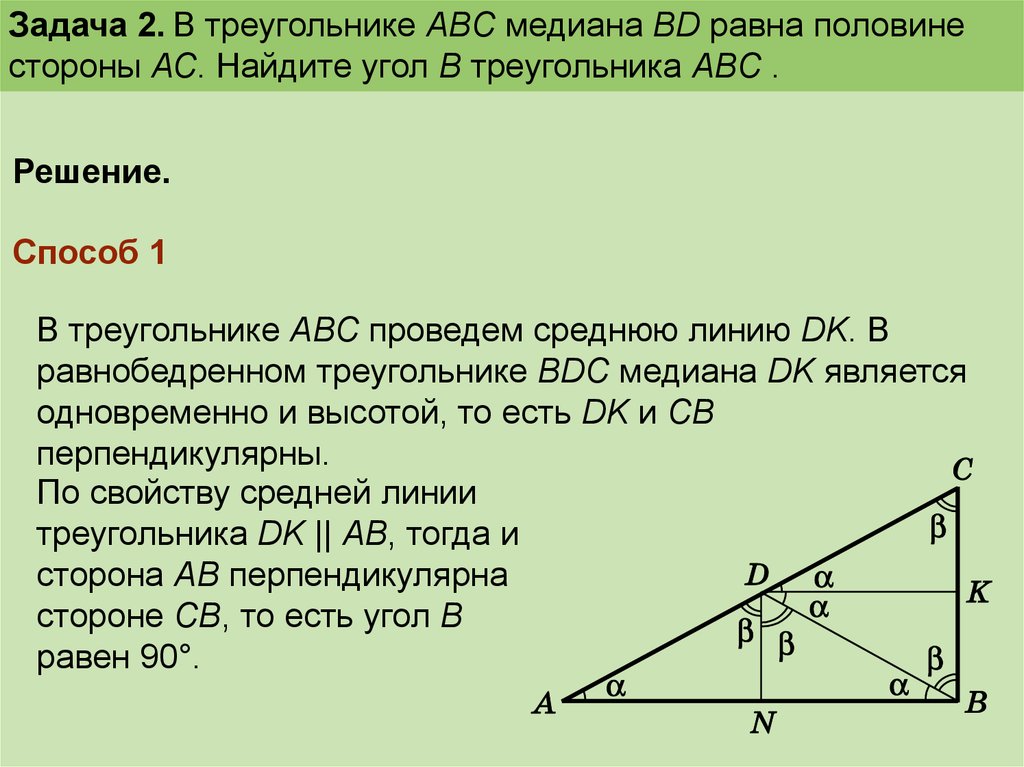
Задача 2. В треугольнике АВС медиана ВD равна половинестороны АС. Найдите угол В треугольника АВС .
Решение.
Способ 1
В треугольнике АВС проведем среднюю линию DK. В
равнобедренном треугольнике BDC медиана DK является
одновременно и высотой, то есть DK и СВ
перпендикулярны.
По свойству средней линии
треугольника DK || AB, тогда и
сторона АВ перпендикулярна
стороне СВ, то есть угол B
равен 90°.
10.
Задача 2. В треугольнике АВС медиана ВD равна половинестороны АС. Найдите угол В треугольника АВС.
Решение.
Способ 2
Обозначим α угол DAB, β – угол DCB. По условию,
BD = AD = DC, значит, угол DBA равен α,
угол DBC равен β. В треугольнике АВС 2α + 2β = 180°,
α + β = 90°, следовательно, угол АВС равен 90° .
11.
Задача 2. В треугольнике АВС медиана ВD равна половинестороны АС. Найдите угол В треугольника.
Решение.
Способ 3
По условию, DA = DB = DC, значит, точки А, В и С
принадлежат окружности с центром D. Тогда угол АВС будет
равен 90° — по свойству вписанного угла, стороны которого
проходят через концы диаметра АС.
12.
Задача 2. В треугольнике АВС медиана ВD равна половинестороны АС. Найдите угол В треугольника.
Решение.
Способ 4
Пусть угол А = α, угол С = β . Проведем DK и DN параллельно
соответственно сторонам АВ и ВС. По теореме Фалеса, они
окажутся средними линиями для треугольника АВС. Медиана
равнобедренного треугольника, проведенная из вершины к
основанию, является и биссектрисой.
При точке D на прямой АС в одной
полуплоскости «скопилось» четыре
попарно равных угла. Сумма всех
четырех равна 180°, 2α + 2β = 180°,
α + β = 90°, следовательно,
угол АВС равен 90°.
13.
Задача 2. В треугольнике АВС медиана ВD равна половинестороны АС. Найдите угол В треугольника.
Решение.
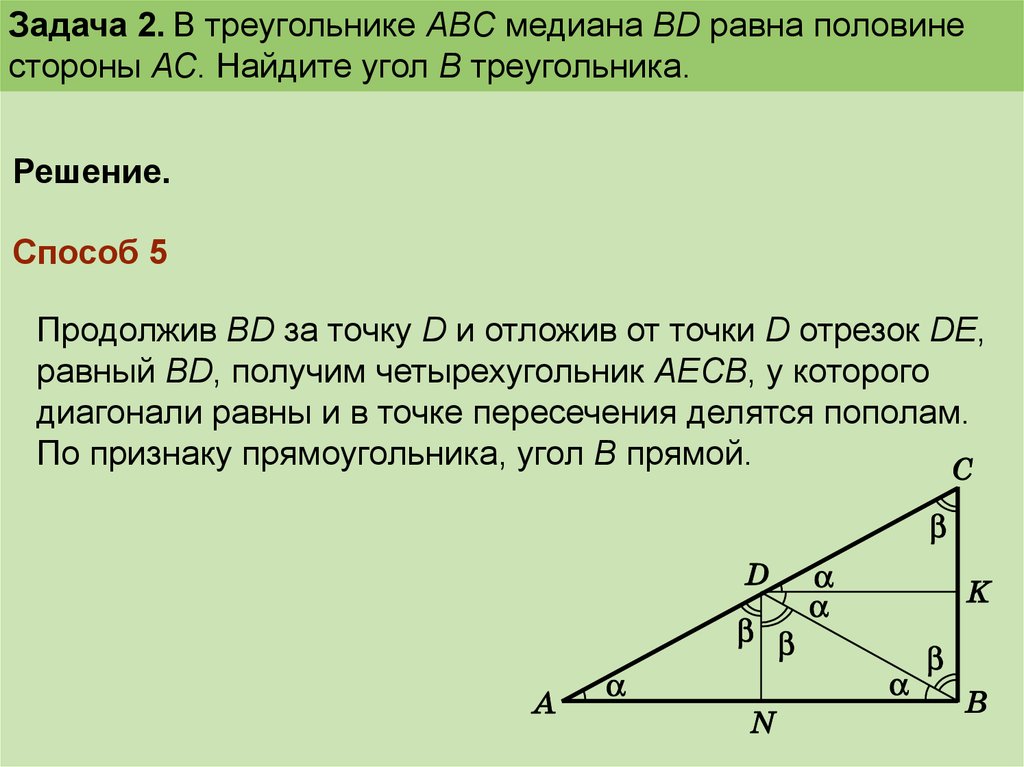
Способ 5
Продолжив BD за точку D и отложив от точки D отрезок DE,
равный BD, получим четырехугольник АEСВ, у которого
диагонали равны и в точке пересечения делятся пополам.
По признаку прямоугольника, угол В прямой.
14.
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 1
Проведя серединный перпендикуляр KО,
получим точку О – центр описанной
окружности (ВK = KС = 6,5 см):
ОВ = ОС = R, OD = BD – OB = 12 – R.
Из треугольника ODC, по теореме
Пифагора, OD2 = ОС2 – DC2 = R2 – 52,
R2 – 52 = (12 – R)2. Решив это
уравнение, получим:
169
R
см.
24
15.
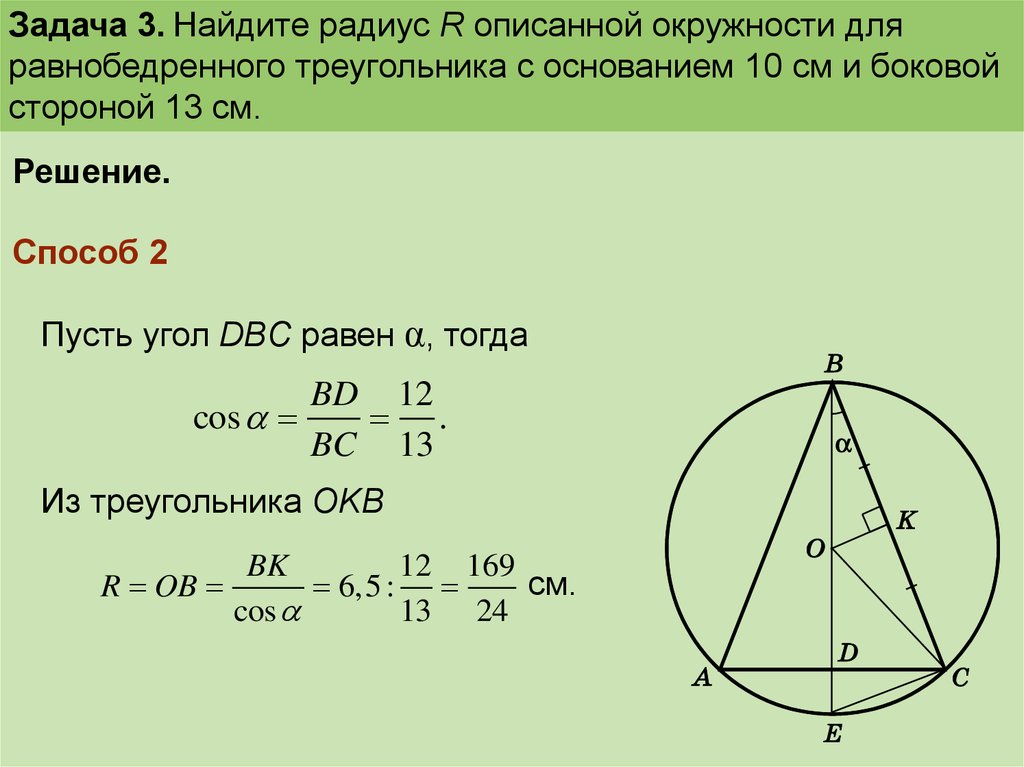
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 2
Пусть угол DBC равен α, тогда
BD 12
cos
.
BC 13
Из треугольника ОKB
R OB
BK
12 169
см.
6,5 :
cos
13 24
16.
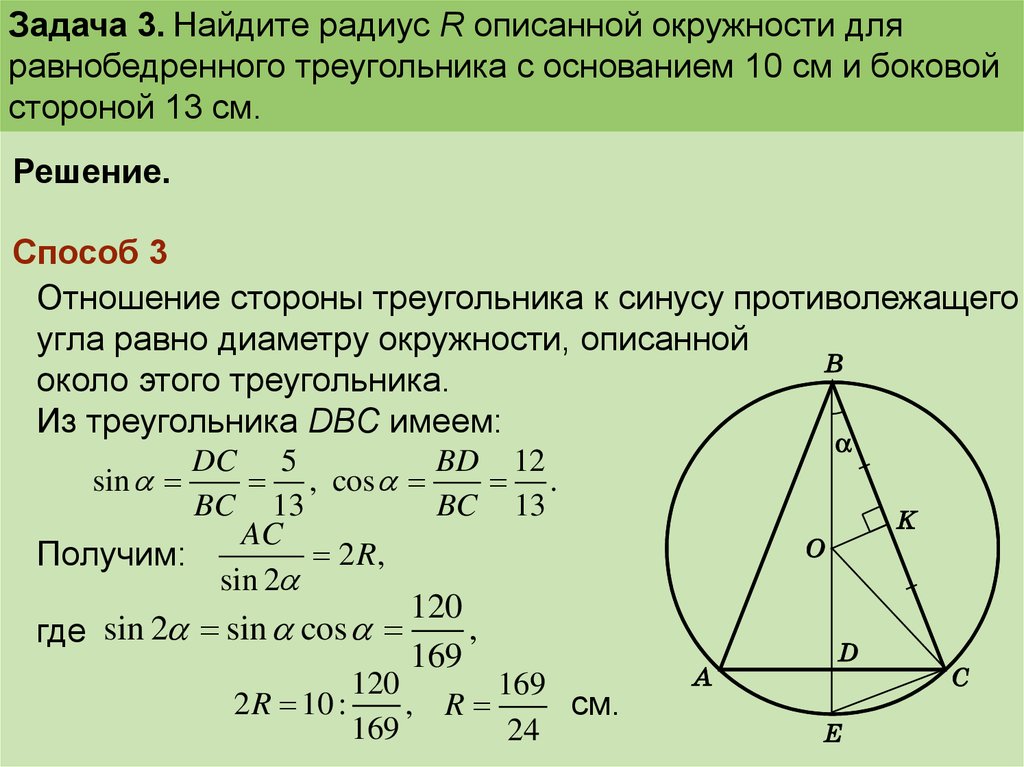
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 3
Отношение стороны треугольника к синусу противолежащего
угла равно диаметру окружности, описанной
около этого треугольника.
Из треугольника DBC имеем:
DC 5
BD 12
sin
, cos
.
BC 13
BC 13
AC
2 R,
Получим:
sin 2
120
,
где sin 2 sin cos
169
120
169
2 R 10 :
, R
см.
169
24
17.
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 4
Из подобия треугольников OBK и CBD имеем:
OB BK R 6,5
,
.
CB BD 13 12
Отсюда
169
R
см.
24
18.
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 5
Продолжим BD до пересечения с описанной окружностью,
получим прямоугольный треугольник ВСЕ,
откуда ВС2 = BD · BE, 132 = 12 · 2R.
Отсюда радиус равен
169
см.
24
19.
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 6
По свойству хорд, пересекающихся внутри круга,
BD · DE = AD · DC, 12 · (2R –12) = 5 · 5.
Решив это уравнение, получим:
R
169
см.
24
20.
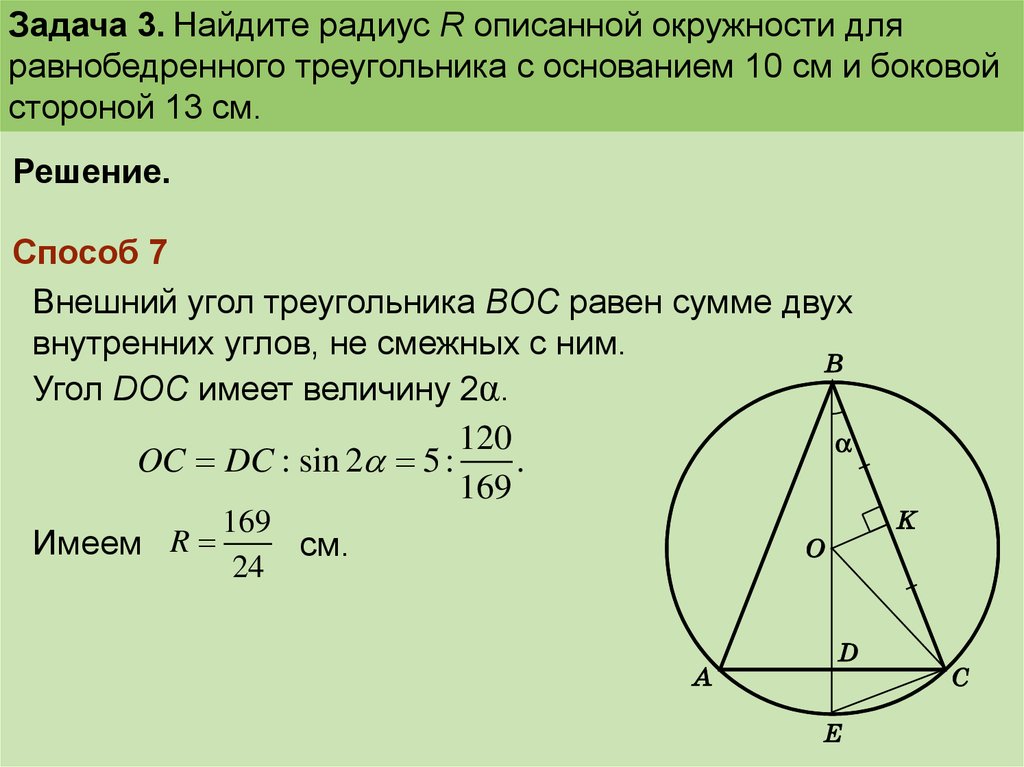
Задача 3. Найдите радиус R описанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 7
Внешний угол треугольника ВOC равен сумме двух
внутренних углов, не смежных с ним.
Угол DOC имеет величину 2α.
120
OC DC : sin 2 5 :
.
169
169
Имеем R
см.
24
21.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 1
Точка О1 – центр вписанной окружности, O1N = r.
В треугольнике BNO1
O1N = r = BO1 · sin α,
5
10
то есть r (12 r )
см.
, r
13
3
22.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 2
Точка О1 – центр вписанной окружности,
O1N = r. DC = CN = 5 см, по свойству
касательных, проведенных из одной точки к
одной окружности.
BN = 13 – 5 = 8 см, ВО1 = 12 – r.
По теореме Пифагора для
треугольника BNO1
r2 = (12 – r)2 – 82,
10
см.
откуда r
3
23.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 3
2S
r
,
a b c
60
r 2
,
13 10 13
10
r см.
3
24.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 4
Из треугольника BNO1 имеем:
r = O1N = BN · tg α.
5
,
Из треугольника BDC tg
12
5 10
поэтому r 8
см.
12 3
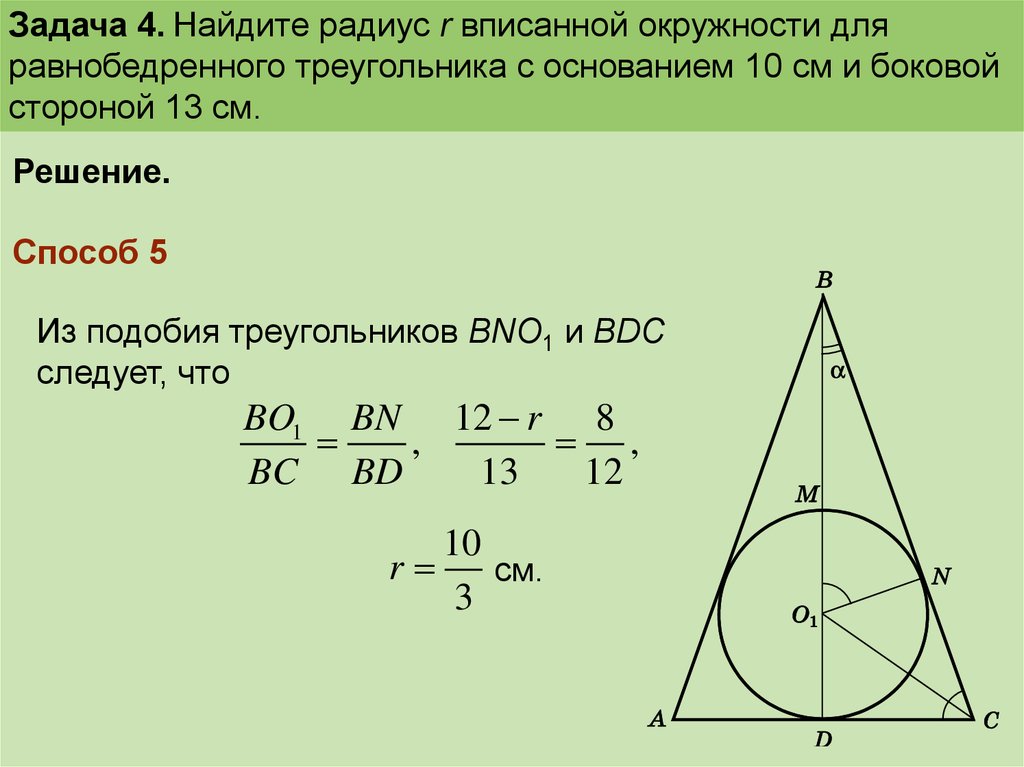
25.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 5
Из подобия треугольников BNO1 и BDC
следует, что
BO1 BN 12 r 8
,
,
BC BD
13
12
10
r
см.
3
26.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 6
По свойству биссектрисы треугольника BDC,
имеем:
CD DO1
5
r
,
,
CB BO1 13 12 r
10
см.
тогда получим r
3
27.
Задача 4. Найдите радиус r вписанной окружности дляравнобедренного треугольника с основанием 10 см и боковой
стороной 13 см.
Решение.
Способ 7
По свойству касательной и секущей,
проведенных из одной точки к одной
окружности: BN2 = BD · BM,
то есть 82 = 12 · (12 – 2r).
10
см.
Откуда r
3
28.
ЗАДАЧА 5В прямоугольном треугольнике ABC на гипотенузе AB
взяты точки E и D так, что AE = AC, BD = BC.
Доказать, что ∠ DCE = 45°.
29.
Способ 1.Треугольники ACE и BCD — равнобедренные, поэтому
CEA 90
A
B
, CDE 90
.
2
2
A B 1
Тогда DCE 180 180
ACB 45 .
2
2 2
30.
Способ 2.Проведем высоту CH. Так как треугольники ACH и BCH
подобны, то ∠ A = ∠ HCB. Треугольник DBC —
равнобедренный, поэтому ∠ CDB = ∠ DCB.
Тогда ∠ A + ∠ ACD = ∠ HCB + ∠ DCH, ∠ ACD = ∠ DCH, а
CD — биссектриса угла ACH. Аналогично, CE —
биссектриса угла HCB.
Следовательно,
90
DCE
45 .
2
31.
Способ 3.Проводим окружности с центрами в точках A и B. Тогда
A
B
ECB
, ACD
,
2
2
A B
ECB ACD
45 .
2
2
Значит,
∠ DCE = 90° – 45° = 45°.
32.
Способ 4.1. Проведем биссектрисы углов A и B в равнобедренных
треугольниках ACE и CBD. AK и BM являются высотами.
90
2. AOB MOK 90
135 .
2
Тогда ∠ DCE = 180° – 135° = 45°.
33.
Способ V1. Проведем медианы AK и BM в равнобедренных
треугольниках AEC и BDC.
2. Точка O — центр описанной окружности около треугольника
DCE и центр вписанной в треугольник ACB окружности.
3. Проведем радиусы OP и OR. Четырехугольник OPCR —
квадрат со стороной r, тогда
OC OD OE 2r .
4. В треугольнике DOE
DE = 2r, DO2 + OE2 = DE2,
след., треугольник DOE —
прямоугольный
и ∠ DOE = 90°, значит,
∠ DCE = 45°.
34.
Способ 61. Впишем окружность в треугольник ACB.
2. PM и KN — касательные к окружности, причем PM ⊥ AB
и KN ⊥ AB, PM ∩ AB = D и KN ∩ AB = E.
3. Проведем радиусы OT + OR = OS = r, тогда
OC OD OE 2r .
4. Опишем окружность
около треугольника DCE
с центром O и радиусом
OC.
5. Тогда
∠DOE=45°+45°= 90°=ᴗDE,
DE 90
DCE
45 .
2
2
35.
Способ 7.1. Треугольники CKE и CPD — равнобедренные, CK = KE и
DP = PC.
180 CKE 180 90 B
B
2. ECK
45
.
2
2
2
A
Аналагично, DCP 45
, тогда
2
B
A B A
DCE 90 45
45
45 .
2
2
2
2
36.
ЗАДАЧА 6.В
прямоугольный
треугольник
вписана
окружность,
перпендикулярно
гипотенузе
проведены
касательные,
пересекающие
гипотенузу в точках D и E. Под каким углом
отрезок DE виден из вершины прямого угла?




























 Математика
Математика








