Похожие презентации:
Взаимное расположение двух окружностей. Общие касательные
1.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕДВУХ ОКРУЖНОСТЕЙ, ОБЩИЕ
КАСАТЕЛЬНЫЕ
2.
Концентрические окружностиКонцентрические окружности – это окружности с
общим центром и различными радиусами.
3.
Взаимное расположение двухокружностей
Если окружности имеют две общие точки, то они
пересекаются
4.
Взаимное расположение двухокружностей
Если две окружности имеют одну общую точку, то они
касаются
Общая точка окружностей – точка касания
Внутреннее касание
Внешнее касание
5.
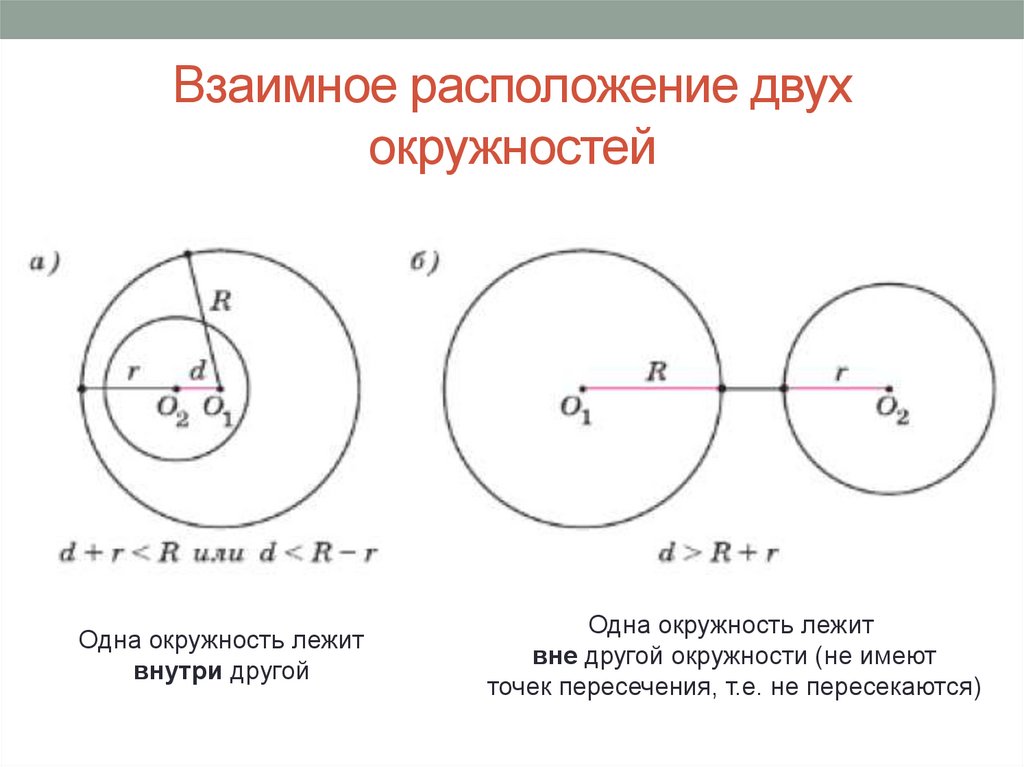
Взаимное расположение двухокружностей
Одна окружность лежит
внутри другой
Одна окружность лежит
вне другой окружности (не имеют
точек пересечения, т.е. не пересекаются)
6.
Теорема7.
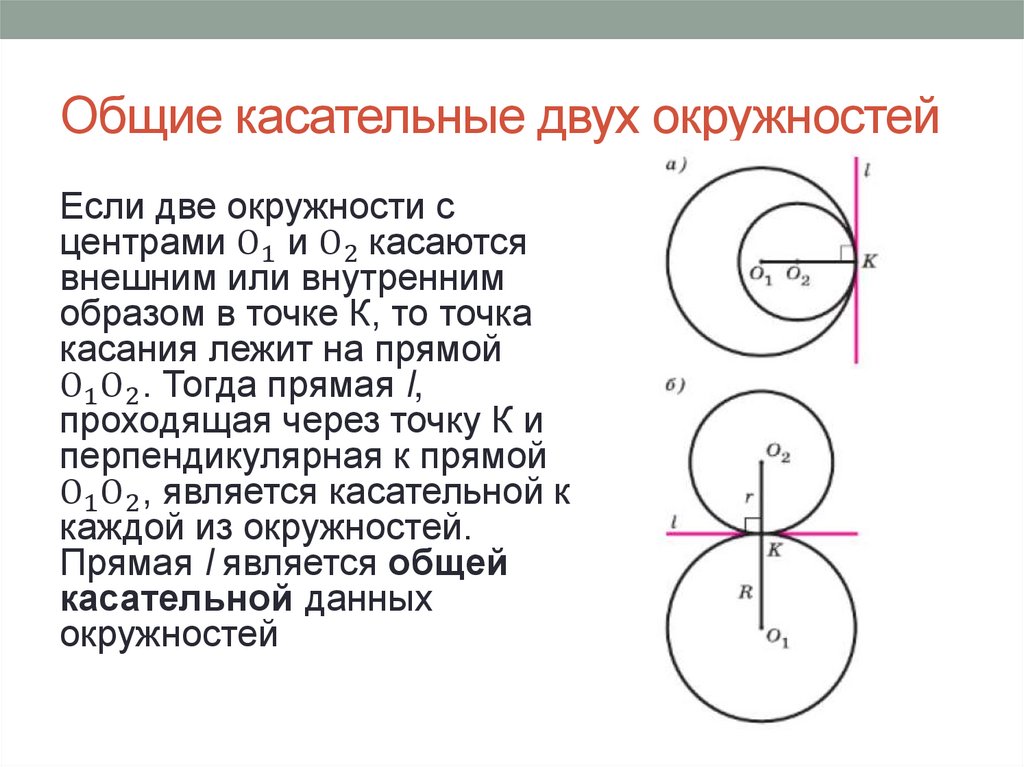
Общие касательные двух окружностейЕсли две окружности с
центрами О1 и О2 касаются
внешним или внутренним
образом в точке К, то точка
касания лежит на прямой
О1 О2 . Тогда прямая l,
проходящая через точку К и
перпендикулярная к прямой
О1 О2 , является касательной к
каждой из окружностей.
Прямая l является общей
касательной данных
окружностей
8.
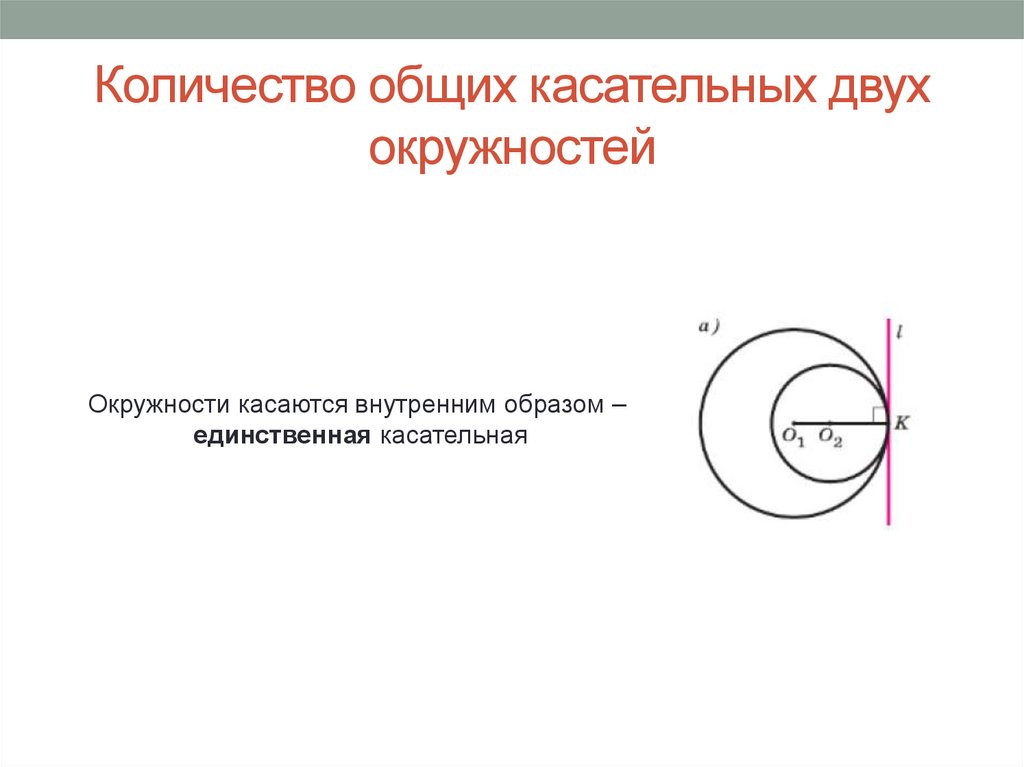
Количество общих касательных двухокружностей
Окружности касаются внутренним образом –
единственная касательная
9.
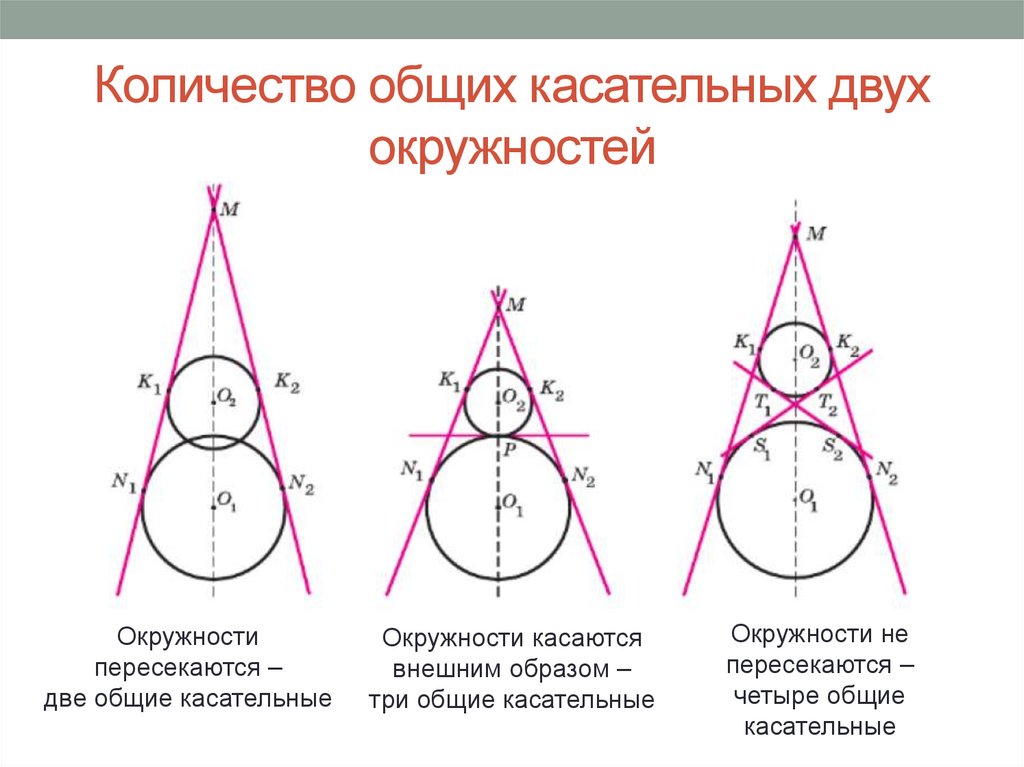
Количество общих касательных двухокружностей
Окружности
пересекаются –
две общие касательные
Окружности касаются
внешним образом –
три общие касательные
Окружности не
пересекаются –
четыре общие
касательные
10.
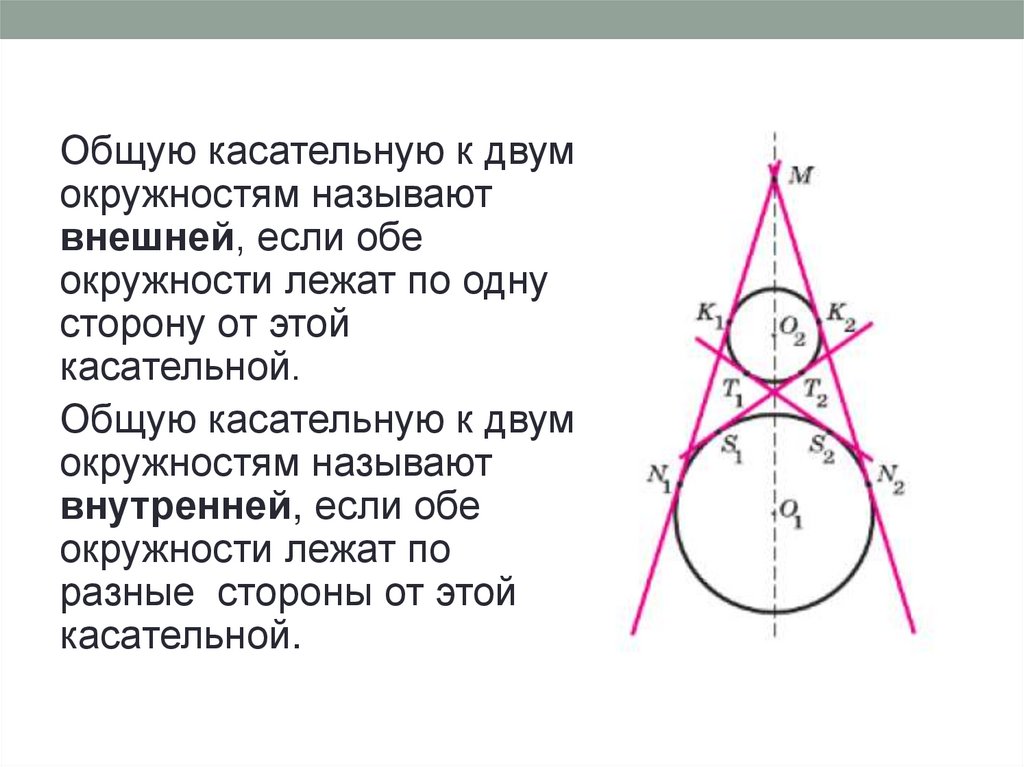
Общую касательную к двумокружностям называют
внешней, если обе
окружности лежат по одну
сторону от этой
касательной.
Общую касательную к двум
окружностям называют
внутренней, если обе
окружности лежат по
разные стороны от этой
касательной.
11.
Домашнее задание:1) п.77, 78 учебника (новый)
2) Решите задачу:
Прямая АВ касается окружности с центром О
радиуса r в точке В. Найдите АВ, если ОА = 2 см, а r =
1,5 см.






 Математика
Математика








