Дискретные случайные величины

1.

2.

3.

4.

5.

6.

7.

8.

9.

Х
х1
х2
…
хi
…
xn
р
p1
p2
…
pi
…
pn

10.

Х
х1
х2
…
хi
…
xn
р
p1
p2
…
pi
…
pn
События Х = х1, Х = х2, …, Х = хn образуют полную
систему попарно несовместных событий, поэтому
сумма их вероятностей равна единице, т.е.
х1
х1

11.

U
Х
р
PP
0
1/4
Х
р
PГ
1
1/4
0
1/4
ГР
1
1/4
1
1/2
2
1/4
ГГ
2
1/4

12.

1. Суммой двух случайных величин X и Y называется
случайная величина, которая получается в результате
сложения всех значений случайной величины Х и всех
значений случайной величины Y, соответствующие
вероятности перемножаются.
двух случайных величин X и Y
называется случайная величина, которая получается в
результате перемножения всех значений случайной
величины Х и всех значений случайной величины Y,
соответствующие вероятности перемножаются.

13.

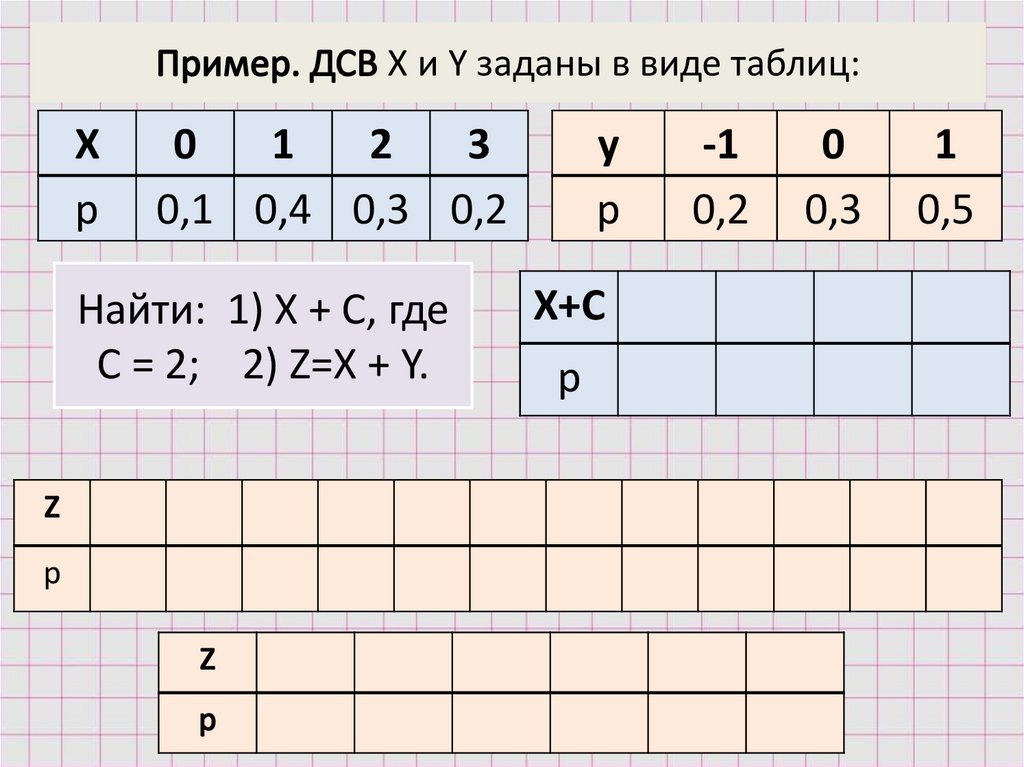
X и Y заданы в виде таблиц:
Х
р
0
1
2
3
0,1 0,4 0,3 0,2
Найти: 1) Х + С, где
С = 2; 2) Z=X + Y.
Z
p
Z
у
р
Х+С
р
-1
0,2
0
0,3
1
0,5

14.

Биномиальное распределение
Пусть случайная величина Х – число появлений события
А в n независимых испытаниях, в каждом из которых
вероятность появления события А равна р, а
непоявления равна q = 1 – p. Очевидно, что Х может
принимать значения 0, 1, 2, …, n, вероятности которых
определяются по формуле Бернулли:
Pn m P X m C p q
m
n
m
n m
, m 0,1,2,..., n.

15.

Определение. Биномиальным распределением
называется закон распределения случайной
величины Х, имеющий вид:
Х
0
1
2
…
m
…
р Сn0 p 0 q n С n1 p1q n 1 Сn2 p 2 q n 2 … Сnm p m q n m …
n
С p q
n
n
Пример. Составить закон распределения числа
попаданий в цель при четырех выстрелах, если
вероятность попадания при одном выстреле
равна 0,9.
n
0

16.

Х
0
1
2
р
0 0 5 0
Р5 Х 0 С5 p q
3
4
5

17.

Пример. Составить закон распределения числа
попаданий в цель при четырех выстрелах, если
вероятность попадания при одном выстреле
равна 0,9.

18.

Упражнения.
1. Составить закон распределения числа попаданий в
цель при шести выстрелах, если вероятность
попадания при одном выстреле равна 0,8.
2. Вероятность того, что студент найдет в библиотеке
нужную ему книгу, равна 0,3. Составить закон
распределения числа библиотек, которые он посетит,
если в городе четыре библиотеки.

19.

20.

21.

Определение. Математическим ожиданием М(Х)
дискретной случайной величины Х называется сумма
произведений всех ее возможных значений хi на их
вероятности pi:
М(Х) = х1р1 + х2р2 + … + хnрn= хiрi
Пример. Найти математическое ожидание случайной
величины Х, зная ее закон распределения:
Х
-1
0
1
2
3
р
0,2
0,1 0,25 0,15 0,3

22.

Свойства математического ожидания
1. Постоянный множитель можно выносить за знак
математического ожидания: М(СХ) = С М(Х).
2. Математическое ожидание суммы двух случайных
величин равно сумме их математических ожиданий:
М(X + Y) = M (X) + M (Y).
3. Математическое ожидание постоянной величины С
равно самой этой величине: М (С) = С.

23.

4. Математическое ожидание любой линейной
комбинации случайных величин равно линейной
комбинации их математических ожиданий:
М ( Сk Хk) = (Сk M (Хk)).
5. Математическое ожидание произведения
независимых случайных величин равно
произведению их математических ожиданий:
M (XY) = M (X) M(Y).

24.

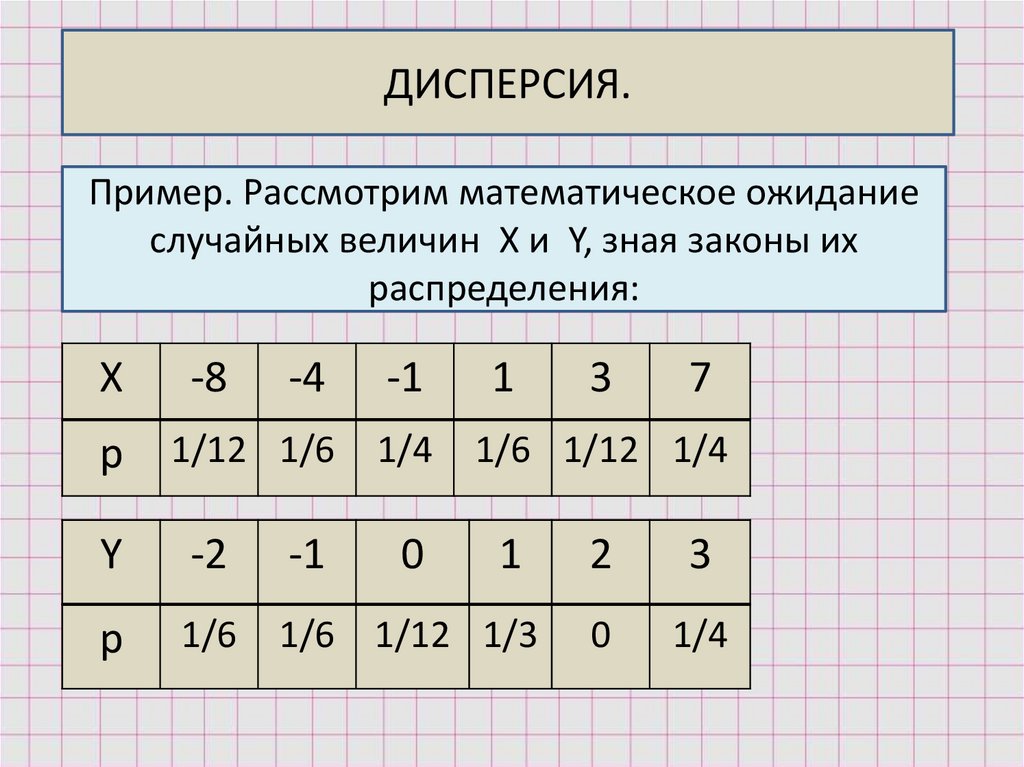
ДИСПЕРСИЯ.
Пример. Рассмотрим математическое ожидание
случайных величин X и Y, зная законы их
распределения:
Х
-8
-4
-1
1
3
7
р
1/12 1/6
1/4
1/6 1/12 1/4
Y
-2
-1
0
1
2
3
р
1/6
1/6 1/12 1/3
0
1/4

25.

Основной числовой характеристикой степени
рассеяния значений случайной величины Х
относительно ее математического ожидания М(Х)
является дисперсия, которая обозначается D (X).
Определение. Отклонением называется разность
между случайной величиной Х и ее
математическим ожиданием М (Х), т.е. Х – М (Х).
Определение. Дисперсией дискретной случайной
величины Х называется математическое ожидание
квадрата ее отклонения: D (X) = М (Х – М (Х))2.

26.

Свойства дисперсии
1. Дисперсия постоянной величины равна нулю:
D (X) = 0.
2. Если Х – случайная величина, а С – постоянная,
то
D (СX) = С2 D (X),
D (X + С) = D (X).
3. Если Х и Y– независимые случайные величины,
то
D (X + Y) = D (X) + D (Y).

27.

Для вычисления дисперсий более удобной
является формула:
D (X) = М (Х2) – (М (Х))2

28.

Пример.
Дискретная случайная величина
распределена по закону:
Х
-1
0
1
2
р
0,2
0,1
0,3
0,4
Найти D(X).

29.

Упражнения
1. Найти математическое ожидание случайной
величины Х, если закон её распределения задан
таблицей:
Х
1
2
3
4
р
0,3
0,1
0,2
0,4
2. На заводе работают четыре автоматические линии.
Вероятность того, что в течение рабочей смены первая
линия не потребует регулировки, равна 09, вторая –
0,8, третья – 0,75, четвертая – 0,7. Найти
математическое ожидание числа линий, которые в
течение рабочей смены не потребуют регулировки.

30.

3. Найти дисперсию случайной величины Х, если
закон её распределения задан таблицей:
Х
1
2
3
4
5
р
0,2
0,4
0,3
0,08
0,02
4. Охотник стреляет по дичи до первого попадания, но
успевает делать не более четырех выстрелов. Найти
дисперсию числа промахов, если вероятность
попадания в цель при одном выстреле равна 0,7.

31.

Контрольные вопросы
1. Дать определение случайной величины.
2. Какая случайная величина называется дискретной?
3. Какое соответствие называется законом распределения
случайной величины Х?
4. Какая случайная величина называется суммой двух
случайных величин X и Y?
5. Какая случайная величина называется произведением двух
случайных величин X и Y?
6. С какими числовыми характеристиками распределения
дискретных случайных величин вы познакомились?
7. Что называется математическим ожиданием М(Х)
дискретной случайной величины Х?
8. Перечислите свойства математического ожидания
дискретной случайной величины Х.
9. Что называется дисперсией дискретной случайной
величины Х?
10.Перечислите свойства дисперсии дискретной случайной
величины Х.