Похожие презентации:
Гидродинамика. Гемодинамика
1. Гидродинамика. Гемодинамика.
1. Стационарное течение. Условиенеразрывности струи. Уравнение Бернулли
2. Вязкость жидкости Уравнение Ньютона.
Кровь, как неньютоновская жидкость.
3. Течение вязкой жидкости по трубам. Формула
Пуазейля. Гидравлическое сопротивление.
4. Ламинарное и турбулентное течение. Число
Рейнольдса
5. Пульсовая волна. Работа и мощность сердца.
2. Стационарное течение. Условие неразрывности струи. Уравнение Бернулли
• Движение жидкости называется течением, асовокупность частиц движущейся жидкости
– потоком.
• Течение жидкости называется
установившимся или стационарным,
если форма и расположение линий тока, а
также значения скоростей в каждой ее точке
со временем не изменяется.
3.
• S1υ1 = S2υ2 = const (1)• уравнение неразрывности
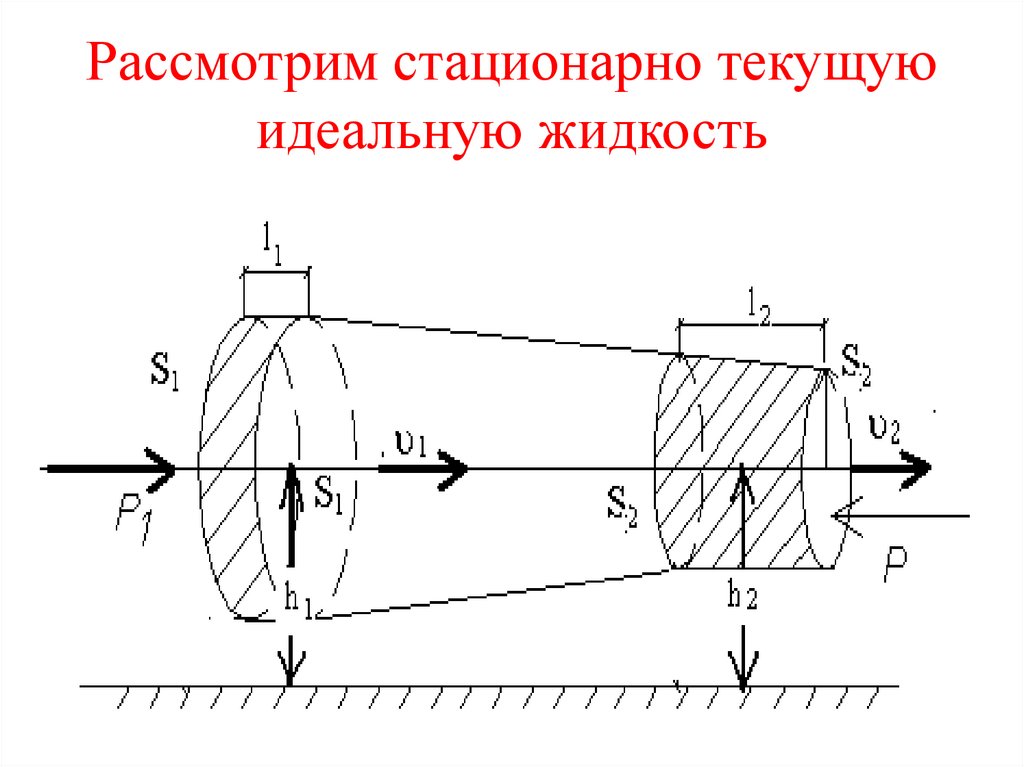
4. Рассмотрим стационарно текущую идеальную жидкость
5.
• За малый промежуток времени ∆tжидкость перемещается от S1 до S1′, и
от S2 до S2′. Согласно закону
сохранения энергии, изменение полной
энергии E2–E1 должна быть равна А –
работе внешних сил.
• E2 – E1 = А
(2)
• где E2 и E1- полные энергии жидкости
массой m в местах сечения S1 и S2.
6.
• С другой стороны, A – это работа,совершаемая при перемещении всей жидкости,
заключенной между S1 и S2 за
рассматриваемый момент ∆t.
• Для перенесения массы m от S1 и S2, жидкость
должна переместиться на
l1 = υ1∆t,
от S1 и S2 на
l2 = υ2∆t, где l1 и l2 малы, υ, ρ и h – const,
следовательно
• A = F1l1+F2l2
(3)
• где F1 = p1S1 и F2 = p2S2.
7.
• Полные энергии E1 и E2, будутскладываться из кинетической и
потенциальной энергии массы m жидкости.
m
E1
mgh1
2
2
1
m
E2
mgh2
2
2
2
(4)
(5)
8.
• Подставим (5) и (4) в (2), и приравняв(2) и (3), получим:
m
mgh 1 p1S1 1 t
2
2
1
m
mgh 2 p 2 S 2 2 t
2
2
2
(6)
9.
• Разделив (6) на ∆V = S1υ1∆t = S2υ2∆tполучим следующее выражение:
2
1
2
gh p1
2
2
2
gh2 p2
• (7)
• где - плотность жидкости, но т.к. сечения
выбираем произвольно, то
10.
2
2
gh p const
(8)
уравнение Бернулли
• где p - статистическое давление (на
поверхности);
- гидродинамическое
2
давление;
• gh - гидростатическое давление.
2
11. Вязкость жидкости Уравнение Ньютона. Кровь, как неньютоновская жидкость.
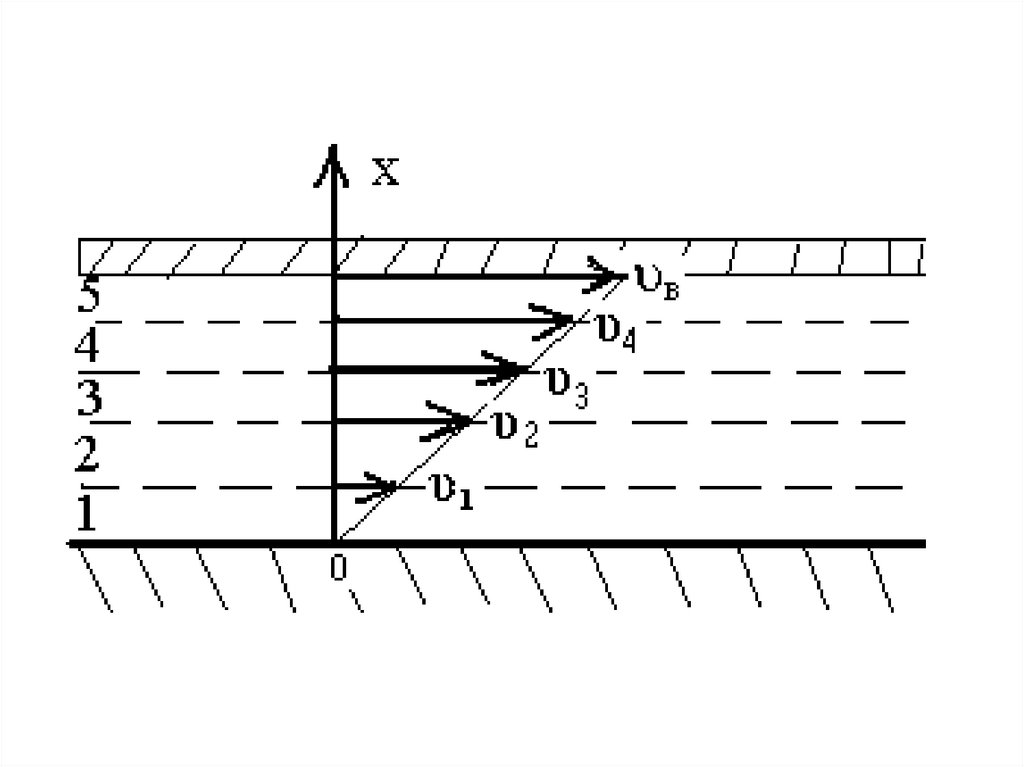
• При течении реальной жидкостиотдельные слои ее воздействуют друг
на друга с силами, касательными к
слоям. Это явление называют
внутренним трением или вязкостью.
12.
13.
dFтр S
dx
где η – коэффициент
пропорциональности, называемый
коэффициентом внутреннего трения
или динамической вязкостью.
(9)
14.
• Жидкости, вязкость которых независит от градиента скорости
называются ньютоновскими.
• Жидкости, вязкость которых
зависит от градиента скорости
называются неньютоновскими.
15.
• Вязкость ньютоновскихжидкостей называют
нормальной,
• а неньютоновских –
аномальной.
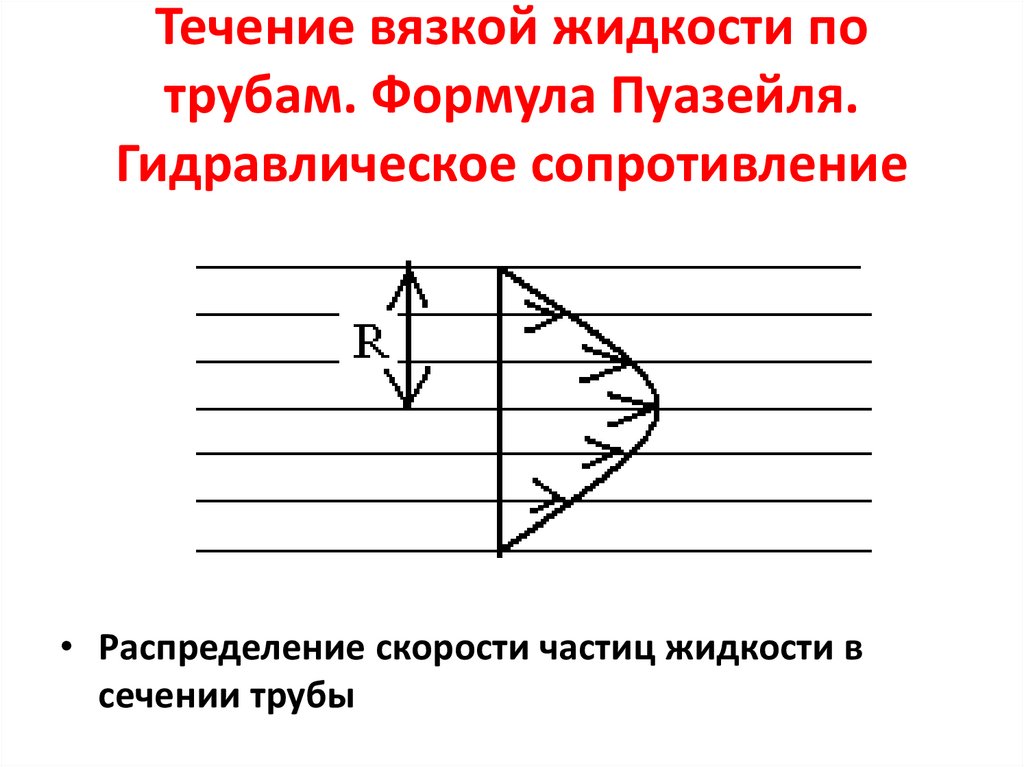
16. Течение вязкой жидкости по трубам. Формула Пуазейля. Гидравлическое сопротивление
• Распределение скорости частиц жидкости всечении трубы
17.
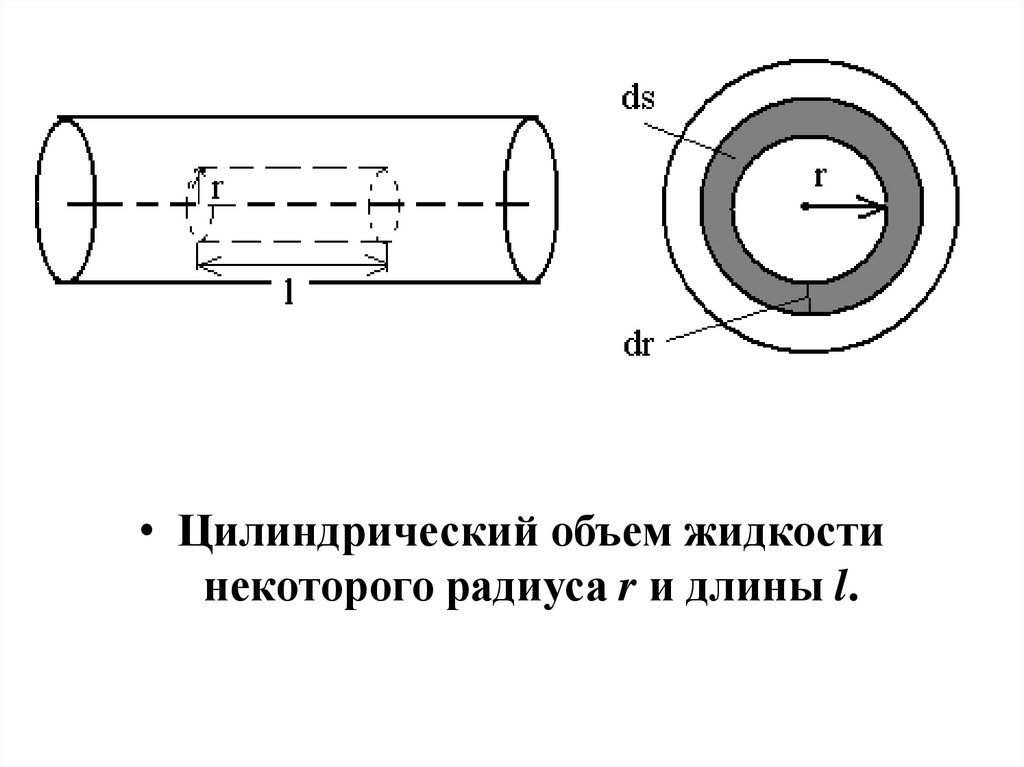
• Цилиндрический объем жидкостинекоторого радиуса r и длины l.
18.
• На торцах этого цилиндраподдерживается давление p1 и p2
соответственно, что обуславливает
результирующую силу
• F = p1πr2– p2πr2 = ( p1 – p2)πr2 (10)
19.
• На боковую поверхность цилиндрасо стороны окружающего слоя
жидкости действует сила
внутреннего трения, равная:
d
d
Fтр S =
(11)
2
r
dx
dr
где S = 2πrl – площадь боковой
поверхности цилиндра.
20.
• Так как жидкость движетсяравномерно, то силы,
действующие на выделенный
цилиндр, уравновешены:
• F = Fтр
(12)
Следовательно:
d
• (p1 – p2)πr2 = – 2 r
dr
(13)
21.
• из выражения (13) имеем:• dυ =
p1 p 2
rdr
2
(14)
• Проинтегрировав выражение (14)
получим:
•υ =
p1 p 2 2 2
(R r )
2
(15)
22.
• Наибольшую скорость имеет слой, текущийвдоль оси трубы (r=0):
• υmax =
( p1 p 2 ) R
4
2
(16)
23.
• Установим, от каких факторовзависит объем Q жидкости,
протекающей через
горизонтальную трубу за 1 с. Для
этого выделим цилиндрический
слой радиусом r и толщиной dr.
Площадь сечения этого слоя
• dS = 2πrdr
24.
• Так как слой тонкий, то можносчитать, что он перемещается с
одинаковой скоростью υ. За 1 с
слой переносит объем жидкости:
• dQ = υdS = υ2πrdr
(17)
• Подставим (16) в (17) получим:
p1 p 2 2 2
(R r )rdr (18)
• dQ =
2
25.
• Проинтегрируем (18) по всемусечению, получим:
p
p
R
1
2
• Q=
8
4
(19)
(19) формула Пуазейля.
• X=8η /(πR4) – гидравлическое
сопротивление.
26.
• При последовательном соединениисосудов:
• Х = Х1+Х2+Х3
(20)
• При параллельном:
• Х=
1
1
1
X1 X 2 X 3
1
(21)
27. Ламинарное и турбулентное течение. Число Рейнольдса.
• Рассмотренное ранее течениежидкости является слоистым, или
ламинарным.
• Увеличение скорости течения вязкой
жидкости по поперечному сечению
трубы создает завихрение, и движение
становится вихревым или
турбулентным.
28.
• Характер течения жидкости по трубезависит от свойств жидкости, скорости
ее течения, размеров трубы
определяется числом Рейнольдса:
• Rе = ρжυD/η
(22)
• где ρж – плотность жидкости;
• D – диаметр трубы
29.
• Так как число Рейнольдса зависит отвязкости и плотности жидкости, то
удобно ввести их соотношение,
называемое кинематической
вязкостью:
• ν = η/ρж (м2/с)
(23)
• Используя это понятие, число
Рейнольдса можно выразить в виде:
• Rе = υD/ν
(24)


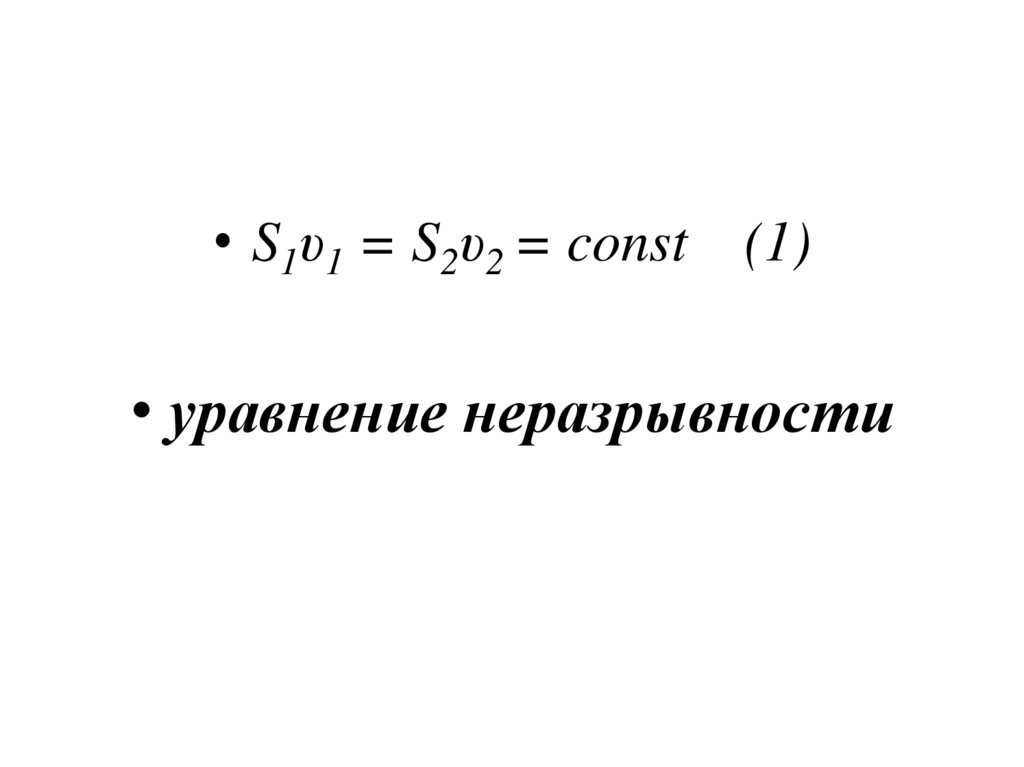























 Физика
Физика








