Простые системы Поста

1. Простые системы Поста

Система Поста (А, В, V, )
Продукция
А – основной алфавит
В – вспомогательный алфавит
V – алфавит переменных
- множество продукций
Система 1: Множество 1 = Wx
( x - слово в {0,1}, включая пустое слово).
аксиома
остальные продукции

2.

Система 2: Множество 2 = Оx
(x – слово в {0,1}, состоящее только из нулей).
аксиома
остальные продукции
Система 3: Множество 3 = Ix
(x – слово в {0,1}, состоящее только из единиц).
аксиома
остальные продукции

3.

Система 4: Множество 4 = NOx
( слова в {0,1}, содержащие хотя бы одну единицу).
Решение 1
аксиома
Решение 2
Одна продукция!
остальные продукции

4.

Система 5 Множество 5 = NIx
(x – слово в {0,1}, содержащие хотя бы один ноль.
Решение 1
аксиома
Решение 2
одна продукция!
остальные продукции

5.

Система 6 Множество 6 : x = y
( x и y – слова в {0,1}одинаковой длины).
аксиомы
остальные продукции
Система 7: Множество 7 : x < y
( слово x короче слова y ).
аксиомы
остальные продукции

6.

Система 8: Множество 8 : Sx
( x – симметричное слово в {0,1}).
аксиомы
остальные продукции
Система 9: Множество 9 : NSx
( x – несимметричное слово в {0,1}).
остальные продукции

7.

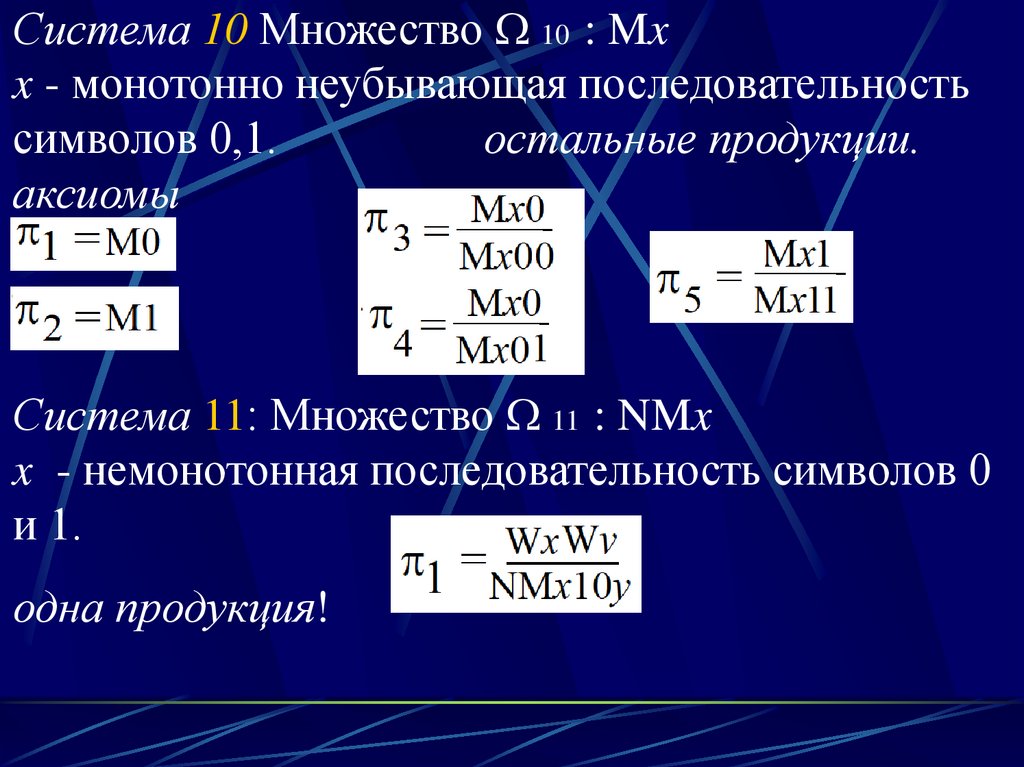
Система 10 Множество 10 : Mx
x - монотонно неубывающая последовательность
символов 0,1.
остальные продукции.
аксиомы
Система 11: Множество 11 : NMx
x - немонотонная последовательность символов 0
и 1.
одна продукция!

8.

Система 12 Множество слов вида E(x , y)
x , y одинаковые слова в {0,1}
остальные продукции.
Система 13: Множество слов вида NE(x , y)
x , y - разные слова в {0,1}
Продукции

9.

Система 14 Множество слов вида Y(x , y)
x , y - слова в {0,1} и
остальные продукции.
Система 15: Множество слов вида Y(x , y)
x , y - слова в {0,1} и
продукции
1
2

10.

Система 16 Множество слов вида Chx
x – cлово в {0,1} четной длины (самостоятельно)
Система 17 Множество слов вида NChx
x - слова в {0,1} нечетной длины (самостоятельно)
Система 18: Множество слов вида x, где x - слово
в {0,1} в котором 0 в два раза больше чем 1.
остальные продукции
аксиомы
Система 19 Множество слов вида (x, y)
x , y – произвольные слова в {0,1}, в которых число 0
различается не более чем в 2 раза. (самостоятельно).

11.

Система 20 Множество слов вида (x , y)
x и y - cлова в {0,1} в которых x – любое, а y
получается из x сжатием всякой последовательности
одинаковых символов в x в один такой символ..
остальные продукции
аксиомы
1
2

12.

Моделирование простых циклов в системах Поста
Система 21 Множество слов вида Max(x , y)
x – произвольное слово в {0,1}, а y – самая длинная
последовательность подряд идущих нулей в x.
остальные продукции
аксиомы
1
2
3

13.

Система 22 Множество слов вида Del(x, y)
x – произвольное слово в {0,1}, y – получается из x
удалением всех самых длинных последовательностей нуле
Решение 1 (цикл с параметром)
вx.
остальные продукции
аксиомы
1
2
3

14.

Система 23 Множество слов вида Del(x, y)
x – произвольное слово в {0,1}, y – получается из x
удалением всех самых длинных
последовательностей нулей в x.
Решение 2 (цикл с предусловием)
одно удаление
старт
завершение
особый случай

15.

Система 24 Множество слов вида del(x, y)
x – произвольное слово в алфавите {0,1}, а y
получается из x удалением всех не самых длинных
последовательностей нулей в x.
одно
удаление
старт
слева
1
2
в середине
3
справа
завершение

16.

Система 25 Множество слов вида col(x, y) =z
x , а – произвольные слова в алфавите {0,1}, z –
количество вхождений y в x.
старт
подсчет
если нет
если да
получение ответа
(если вышли)

17.

Система 26 Множество слов вида col(x, y) =z
x , а – произвольные слова в алфавите {0,1}, z –
максимальное количество вхождений y в x без
пересечений.
подсчет
старт
если нет
если да
получение ответа
(если вышли)

18.

Система 27 Множество слов вида col(x, y) =z
x , а – произвольные слова в алфавите {0,1}, z –
максимальное количество симметричных
вхождений y в x. (самостоятельно)