Виды проекций и пространственные координаты точек, используемые в геодезии. Решение основных геодезических задач

1.

Виды проекций и пространственные координаты
точек, используемые в геодезии. Ориентирующие
углы земных линий и формулы их взаимосвязей.
Решение основных геодезических задач.
Быкова А.А.

2. Виды проекций и пространственные координаты точек, используемые в геодезии.

Одной из важнейших задач геодезии является изображение физической поверхности Земли на
плоскости (листах бумаги) в виде топографических чертежей (карт, планов, профилей). При этом
изучение соотношений пространственных фигур земной поверхности производится на основе
проектирования земных точек на поверхность эллипсоида вращения или на основную уровенную
поверхность, которые в определенных пределах (для участков с размерами до 20км) могут быть
приняты за горизонтальную плоскость.
В геодезии различают следующие виды проекций: ортогональная (основная), центральная и
картографическая.
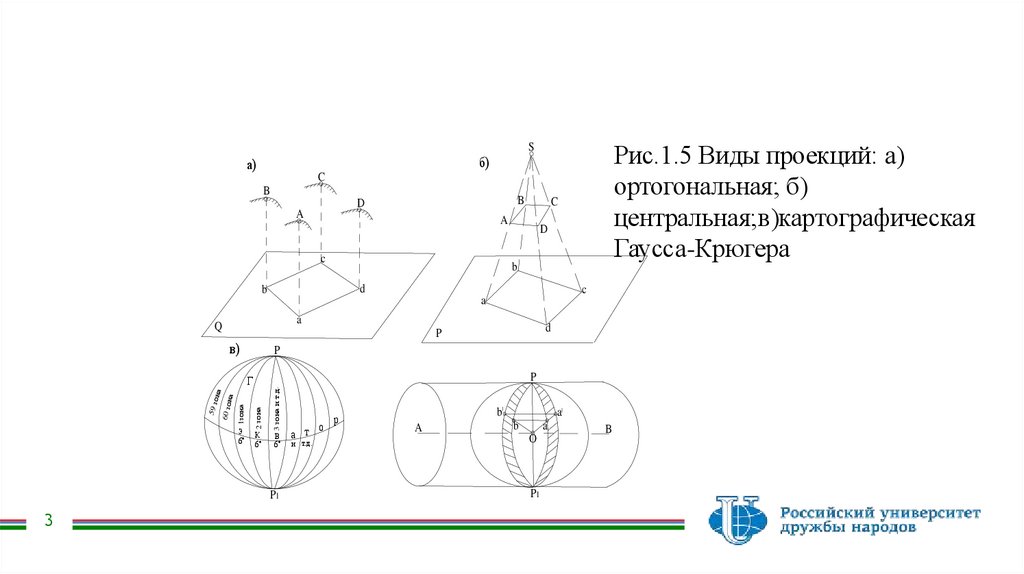
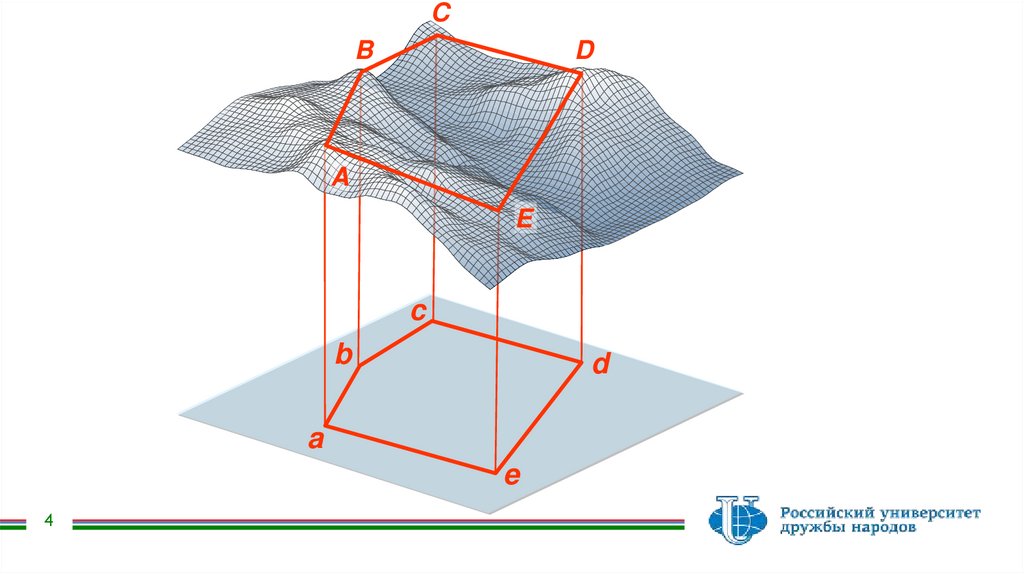
Ортогональная проекция (рис.1.5,а) предусматривает проектирование точек земной
поверхности отвесными линиями на плоскость проекций (поверхность эллипсоида вращения или
основную уровенную поверхность). В пересечении отвесных линий с поверхностью проекций
получают точки (a, b, с, d на рис.1.5,а), которые называют горизонтальными проекциями земных
точек ( А,В,С, Д на рис.1.5,а). При этом угол β равен проекции этого угла β', а горизонтальные
проекции линий - их горизонтальным проложениям (s). При проектировании сравнительно
небольших участков местности (площадью круга до 320 км²) уровенную поверхность заменяют
горизонтальной плоскостью. В этом случае отвесные линии будут параллельны друг другу и
перпендикулярны к плоскости проекций (рис.1.5,а).
2

3.

Рис.1.5 Виды проекций: а)
ортогональная; б)
центральная;в)картографическая
Гаусса-Крюгера
S
б)
а)
C
B
B
D
A
c
D
b
d
b
c
a
a
Q
P
P
1зона
2 зона
3 зона и т.д.
Г
59 з
она
60 зо
на
d
P
в)
6°
6°
6°
э к
о
в а т
P1
3
C
A
и т.д.
р
b
A
a
a
b
O
P1
B

4.

C
B
D
A
E
c
b
d
a
e
4

5.

Центральная проекция (рис.1.5,б) основана на том, что проектирование производится из одной точки
(полюса Р – центра проекций – рис.1.5,б). Точки а, b, с, d на рис.5 являются центральными проекциями
четырехугольника ABCD. Данный вид проекции применяется в фототопографии.
Картографические проекции (рис.1.5,в) применяются для изображения на плоскости значительных
территорий земной поверхности. Эти проекции дают возможность переносить (проектировать) точки с
поверхности эллипсоида на плоскость по определенным математическим законам. В общем случае
картографические проекции могут быть построены без искажения длин(и тогда их называют
равновеликими) или без искажения углов (в этом случае их называют равноугольными, или конфорными).
В геодезии широко применяется равноугольная зональная поперечно- цилиндрическая проекция ГауссаКрюгера (рис.1.5,в), при которой возникающие искажения длин (площадей) являются сравнительно
незначительными и могут быть учтены достаточно несложными формулами. Сущность указанной проекции
заключается в следующем. Земной эллипсоид делится меридианами на зоны. Проектирование точек
производится в пределах каждой зоны из центра эллипсоида на поверхность огибающего цилиндра.
Центральный угол проектирования (λ) остается постоянным. Зоны могут быть 6-ти или 3-х градусные (λ =
6˚ или λ = 3˚). Проекция зоны на цилиндр больше, чем ее размеры на эллипсоиде (относительная
величина искажения длин линий может быть определена по формуле εℓ = Y²/2R², где Y – расстояние от
осевого меридиана зоны до средней точки линии; R – радиус земного сфероида). После проектирования
каждой зоны (на основе их поворота вокруг полярной оси) цилиндр разворачивается в плоскость и тем
самым получают плоские изображения зон. Проекция Гаусса-Крюгера используется в геодезии для
построения в зонах системы прямоугольных координат.
5

6.

При оценке пространственного положения земных точек используют географическую,
зональную прямоугольную и высотную системы координат.
К географическим координатам земных точек относятся (рис.1 ): 1) широта (φ) –
угол между плоскостью экватора Земли и отвесной линией, проходящей через точку; 2)
долгота (λ) – двугранный угол между плоскостью Гринвичского (нулевого) меридиана и
плоскостью меридиана, проходящего через точку.
Начало отсчета широт – линия экватора, долгот – плоскость Гринвичского меридиана.
Широты могут быть северными и южными с пределами их изменения от 0˚ до 90˚,
долготы – западными и восточными с пределами их изменения от 0˚ до 180˚.
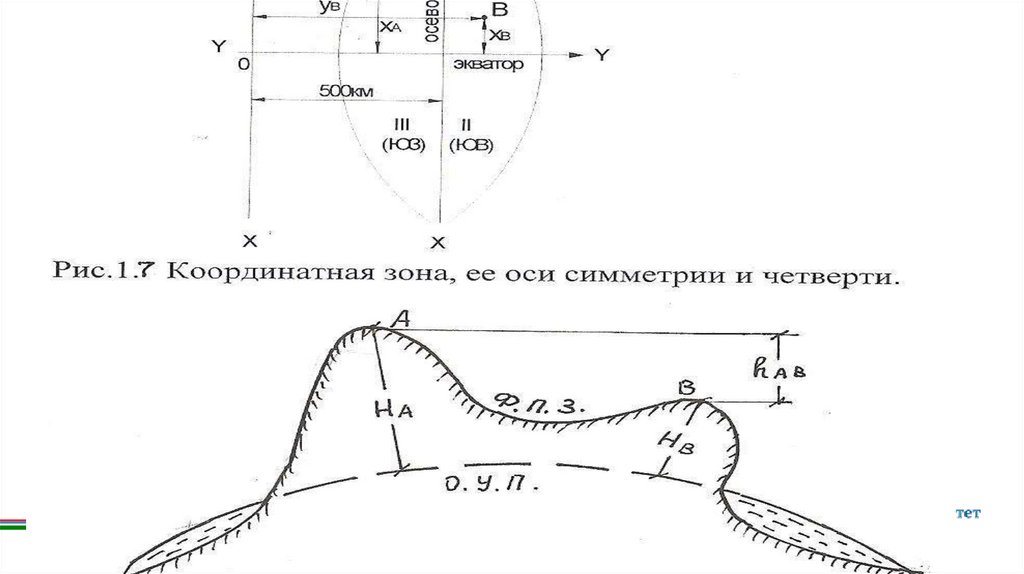
К зональным прямоугольным координатам точки относятся (см. рис.1.7):
1) абсцисса (Х) – расстояние от точки до линии экватора;
2) ордината (Y) – расстояние от точки до условной линии, параллельной осевому
меридиану координатной зоны и находящейся 500км к западу от него. Перед значением
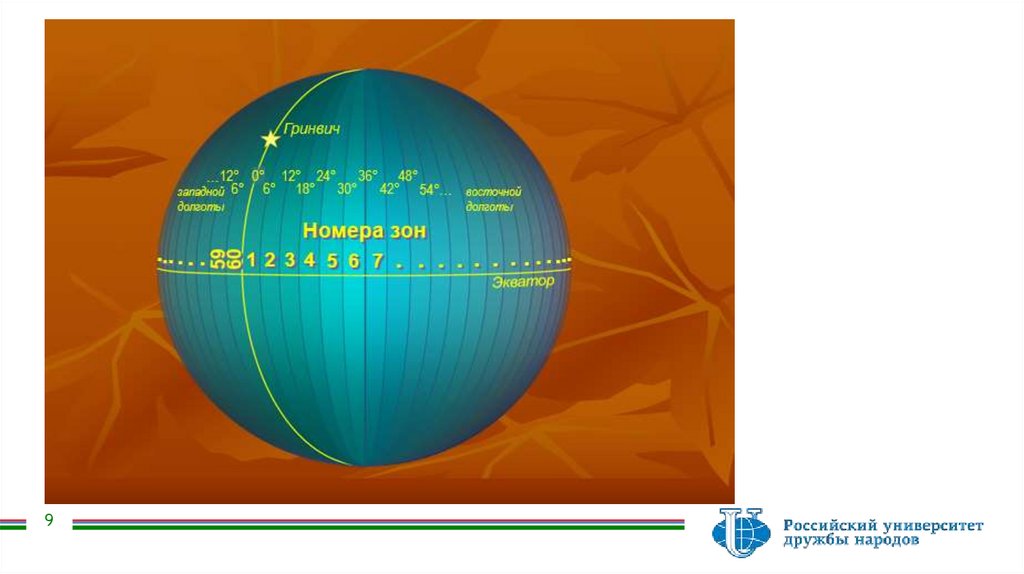
ординаты точки указывается (приписывается номер зоны). Координатной зоной принято
считать часть земной поверхности, ограниченной 2-мя меридианами с разницей долгот в
6˚. Счет зон производится от Гринвичского меридиана с долготой 0˚ в направлении на
восток (1,2….60).
6

7.

7

8.

Пересечение осей симметрии зоны образует ее 4 координатные четверти с нумерацией по ходу часовой
стрелки от северного направления осевого меридиана зоны. Координатным четвертям соответствует
обозначения: I – СВ(северо-восточная); II –ЮВ (юго-восточная); III – ЮЗ (юго-западная); IV – СЗ (северозападная).
Разность координат 2-х точек называют приращением координат. Их соответственно обозначают ΔХ и ΔY
(см. рис. 1.7) и определяют по формулам
ΔХAB = XB - XA
(1.11)
ΔYAB = YB – YA
(1.12)
где X и Y – прямоугольные координаты соответственно точек В и А. Приращения координат могут иметь
знаки (+) или (-).
Высотной координатой точки является ее высота (см. рис.1.8). Высота - это расстояние от точки до
О.У.П. (основной уровенной поверхности). Высота О.У.П. принимается равной 0 м. Высоты точек (Hi) могут
иметь знаки (+) или (-) в зависимости от того находятся они выше или ниже О.У.П. В России используется
Балтийская система высот, для которой началом отсчета высот является средний уровень Балтийского
моря, отмеченный на Кронштадском футштоке Рижского залива (г. Санкт – Петербург, Россия).
Разность высот двух точек называют превышением (h). Согласно рис. 1.8 на примере линии АВ можно
записать
hАВ = НВ – НА
(1.13)
где НВ и НА – высоты соответственно точек В и А.
Превышения могут иметь знаки (+) или (-).
8

9.

9

10. Ориентирующие углы земных линий и формулы их взаимосвязей

В геодезии для характеристики направления линий в проекции на горизонтальную
плоскость используют значения их ориентирующих углов. Ориентировать линию – это
значит определить ее положение относительно исходного направления. В качестве
исходных направлений в геодезии принимают:1) магнитный меридиан 2)
географический меридиан; 3)осевой меридиан координатной зоны. Соответственно
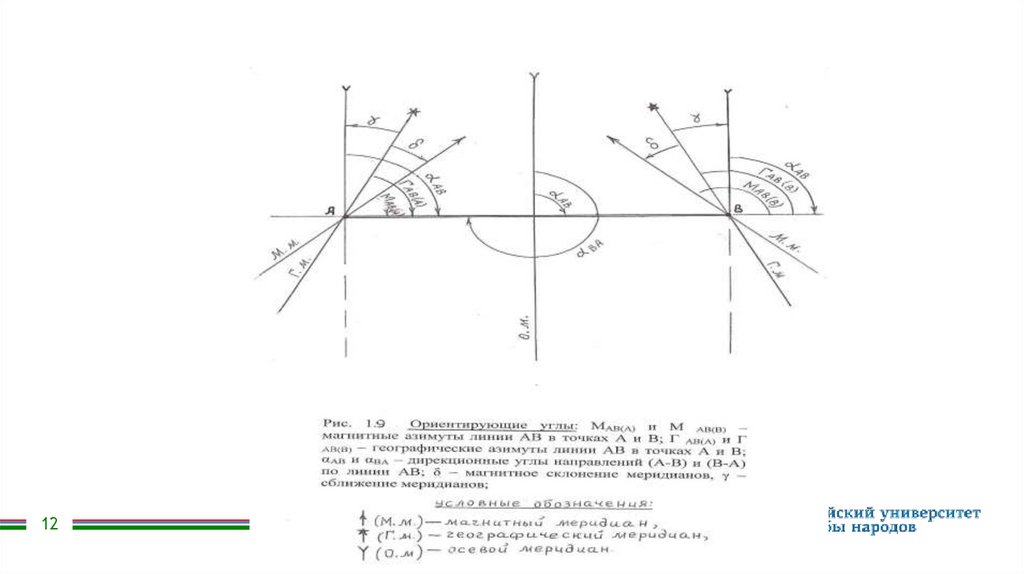
различают следующие ориентирующие углы (рис. 1.9):
- магнитный азимут (М) – горизонтальный угол, отсчитываемый по ходу часовой
стрелки от северного направления магнитного меридиана до ориентируемой линии;
- географический азимут (Г) – горизонтальный угол, отсчитываемый по ходу часовой
стрелки от северного направления географического меридиана до ориентируемой
линии;
- дирекционный угол (α) – горизонтальный угол, отсчитываемый по ходу часовой
стрелки от северного направления осевого меридиана (или линии, параллельной ему)
до ориентируемой линии.
Разность между географическим и магнитным азимутами называется магнитным
склонением меридианов и обозначается как
10

11.

δ=Г-М
(1.14)
а разность между географическим азимутом и дирекционным углом – сближением
меридианов с обозначением
γ=Г-α
(1.15)
Согласно (1.14) и (1.15) взаимосвязь ориентирующих углов выражается следующими
формулами:
Г=М+δ
(1.16)
α = Г - γ =М+ δ – γ
(1.17)
Склонение и сближение меридианов могут быть восточными (т.е. располагаться к
востоку от географического меридиана) и иметь знак (+) или западными (т.е.
располагаться к западу от географического меридиана) и иметь знак (-).
11

12.

12

13.

Азимуты и дирекционные углы могут принимать значения от 0˚ до
360˚. Отличие азимутов от дирекционных углов состоит в том, что
значение дирекционного угла постоянно для любой точки
ориентируемой линии (α = сonst), а значения азимутов переменны в
зависимости от положения точки на линии (М, Г ≠ const). Указанное
свойство дирекционных углов обуславливает их преимущественное
использование в качестве ориентирующих углов линий (примеры α =
const и М(Г) ≠ const см. рис. 1.9).
Для одной и той же линии следует различать дирекционные углы
(также как и азимуты) прямого (αпр) и обратного (αобр)
направлений линий (см. αАВ и αВА на рис.1.9). Разница между
прямыми и обратными значениями ориентирующих углов можно
выразить формулой:
αобр = αпр + 180º
(1.18)
13

14.

При αпр > 180º в формулу (1.18) следует вводить значение (-360º), чтобы избежать получения
αобр > 360º.
В качестве косвенных характеристик ориентирующих углов могут служить румбы (r), т.е.
острые углы (в пределах от 0˚ до 90˚), отсчитываемые от ближайшего, северного или
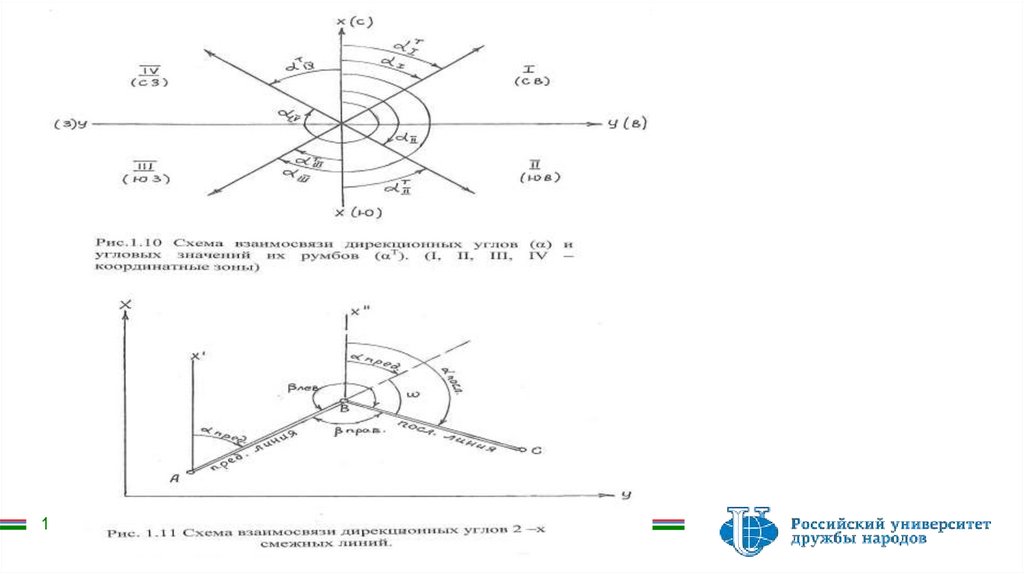
южного, направления меридиана до ориентируемой линии (cм. рис.1.10 на примере
дирекционных углов). Румб обозначается записью координатной четверти и числового
значения.
Пример: r = CЗ: 45˚ (северо-западная координатная четверть, числовое значение румба
45˚).Числовое значение румба называют табличным углом (αТ).
В зависимости от координатных четвертей взаимосвязь между дирекционным углом и
табличным углом румба (согласно рис.1.10) может быть выражена формулами:
а) I четверть (СВ):
α = αТ
б) II четверть (ЮВ): α = 180˚- αТ
в) III четверть (ЮЗ): α = αТ + 180˚
г) IV четверть (СЗ): α = 360˚- αТ
14
(1.19)
(1.20)
(1.21)
(1.22)

15.

15

16.

Учитывая превалирующую роль дирекционных углов(для ориентирования земных линий) рассмотрим
схему взаимосвязи дирекционных углов двух смежных линий, приведенную на рис.1.11. Согласно
этой схеме дирекционные углы последующей (αпосл.) и предыдущей (αпред.) линий взаимосвязаны друг с
другом через соответствующие значения горизонтальных углов ( βпр – правого по ходу линий и βлев –
левого по ходу линий). В соответствии с рис. 1. можно записать,что
αпосл. = αпред + ω
(1.23)
или с учетом выражений
ω = 180º- βпр
βпр = 360º - βлев
(1.24)
(1.25)
в окончательном виде получаем
αпосл.= αпред + 180º - βпр
αпосл.= αпред - 180º+βлев
16
(1.26)
(1.27)

17.

При расчетах по формулам (1.26) и (1.27) необходимо учитывать
следующие два условия:
1) в случае получения значения αпред > 360° от расчетного результата
следует вычесть 360° и полученное значение считать искомым углом; 2) в
случае получения отрицательных значений αпосл к расчетному результату
следует прибавить 360° и полученное значение считать искомым углом.
Примеры: 1) при значениях αпред =310°и βправ = 20° по формуле (1.26)
получаем αпосл = 310° + 180° -20° = 470°; поскольку дирекционный угол не
может быть больше 360°, то в качестве искомого угла записываем
значение αпосл = 470° -360° = 110° ; 2) при значениях αпред = 40° и βлев = 70°
по формуле (1.27) получаем αпосл = 40° -180° + 70° = - 70°; поскольку не
может быть отрицательных значений дирекционного угла, то в качестве
искомого угла записываем значение αпосл = 360° -70° = 290°.
17

18.

Если для двух направлений выходящих из одной точки (т.В на рис. 1.11)
известны дирекционные углы (αВА и αВС), то горизонтальный угол между
направлениями (βправ) равен разности их дирекционных углов, что можно
записать как:
АВС = αВА – αВС
(1.28)
где βАВС – горизонтальный угол между линиями (ВА) и (ВС), правый по ходу
(А-В-С).
При получении по формуле (1.28) отрицательных значений βАВС, т.е. для
случаев αВА < αВС к расчетному результату добавляют 360° и полученное,
положительное
значение принимается за искомую величину βАВС.
18

19. Решение основных геодезических задач

К основным геодезическим задачам прежде всего
следует отнести задачи, связанные с определением
приращений координат и координат точек земной
поверхности, дирекционных углов и горизонтальных
проложений земных линий, превышений и высот точек
Земли. В первую очередь среди таких задач можно
указать
на: 1) прямую геодезическую задачу; 2)
обратную
геодезическую
задачу
и
3)
задачи
геодезического
нивелирования
(определение
превышений и высот ). Решение указанных задач, как
правило, составляет основу алгоритмов решения
остальных геодезических задач.
19

20.

Сущность прямой геодезической задачи состоит в том, что по
координатам одной точки (ХА,YА) прямой линии, ее дирекционному углу (αАВ)
и горизонтальному проложению (sАВ) вычисляют приращения координат (∆ХАВ
=?,∆YАВ =?) и прямоугольные координаты другой точки этой линии (ХВ=?,YВ=?).
Схема решения прямой геодезической задачи(на примере I координатной
четверти) очевидна из рис.1.12; ее расчетными формулами (общими для
всех координатных четвертей) являются выражения:
∆ХАВ = sАВ ·cos αАВ
(1.29)
∆YАВ = sАВ ·sin αАВ
(1.30)
ХВ= ХА +∆ХАВ = ХА + sАВ ·cos αАВ
(1.31)
YВ= YА+∆YАВ = YА+ sАВ ·sin αАВ
(1.32)
При расчетах по формулам (1.29 – 1.32) следует учитывать знаки
тригонометрических функций дирекционного угла αАВ, зависящих от
величины αАВ.
20

21.

21

22.

Сущность обратной геодезической задачи
состоит в том, что по координатам (ХА,YА, ХВ,YВ)
конечных
точек
линии
вычисляют
ее
дирекционный угол (αАВ=?) и горизонтальное
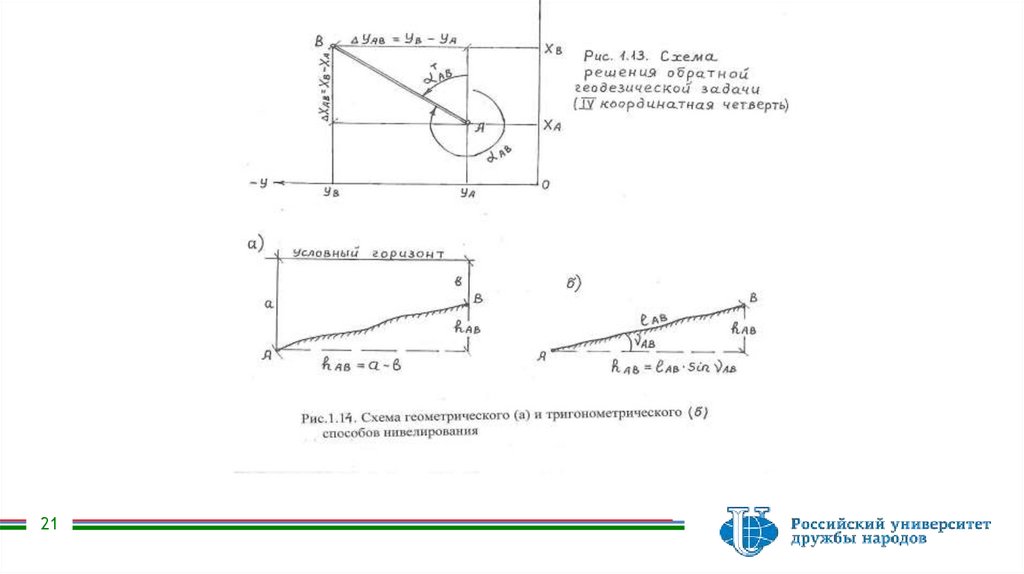
проложение (sАВ=?).Схема решения обратной
геодезической
задачи
(на
примере
IV
координатной четверти), понятна из рис. 1.13; ее
расчетными формулами (общими для всех
координатных четвертей) являются выражения
22

23.

23

24.

Cущность задачи геодезического нивелирования заключается в
определении превышений и высот точек земной поверхности и
основано на применении геометрического и тригонометрического
способов. Отметим, что нивелированием в геодезии называют
определение высотного взаимоположения определяемой точки с
другими точками с известными (заранее установленными)
высотами.
При геометрическом нивелировании превышения определяют
как разность отвесных расстояний, измеренных от нивелирных
точек до условных горизонтальных линий (рис.1.14а), т.е. по
формуле
24

25.

25