Похожие презентации:
Алгебра высказываний
1. Алгебра высказываний
2. Условия для получения автомата
3. Понятие высказывания
4. Понятие высказывания
5. Основные логические операции и таблицы истинности
6. Конъюнкция
7. Конъюнкция
A0
0
1
1
B
0
1
0
1
A&B
0
0
0
1
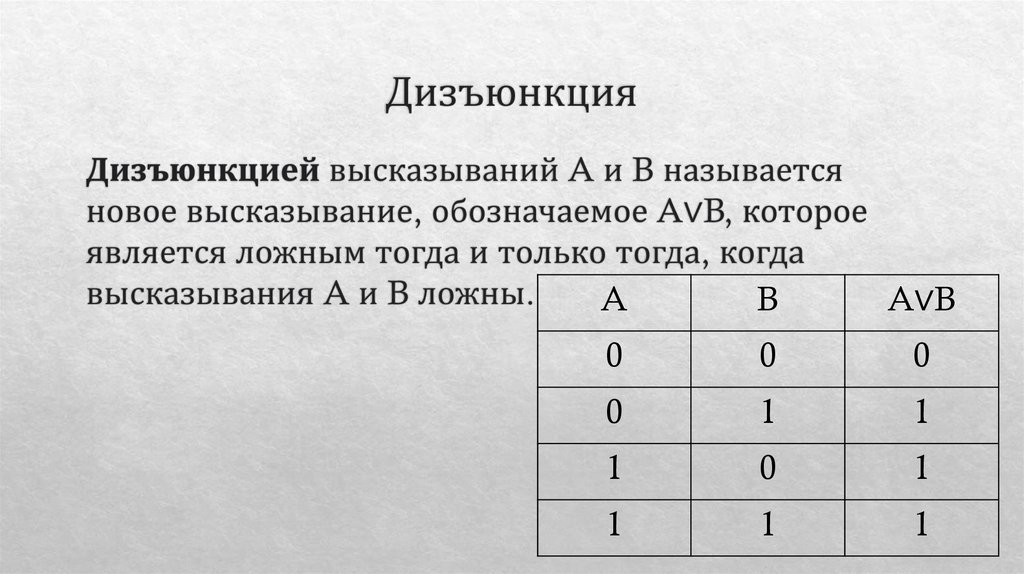
8. Дизъюнкция
9. Дизъюнкция
AB
A∨B
0
0
0
0
1
1
1
0
1
1
1
1
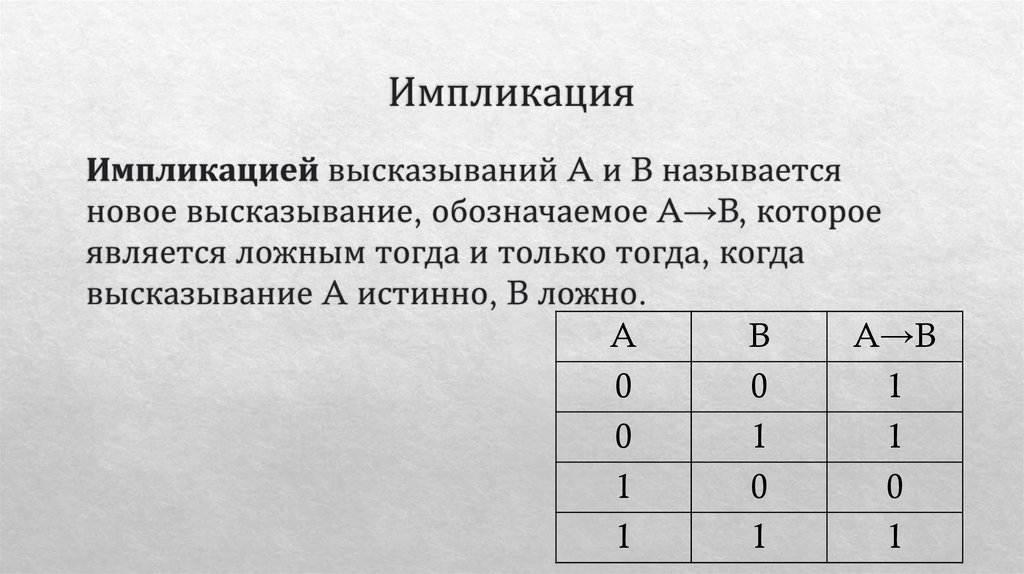
10. Импликация
11. Импликация
A0
0
1
1
B
0
1
0
1
A→B
1
1
0
1
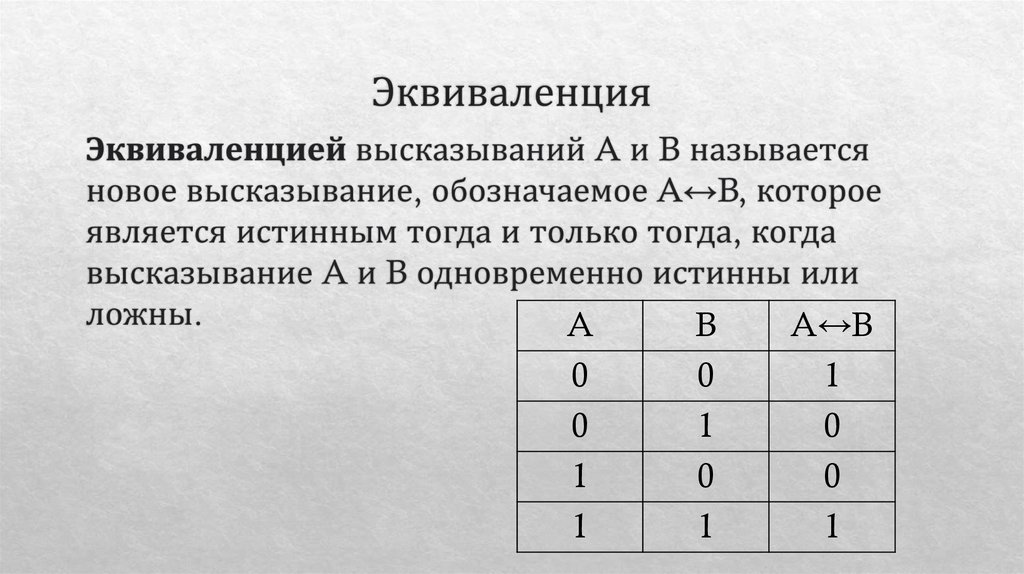
12. Эквиваленция
13. Эквиваленция
A0
0
1
1
B
0
1
0
1
A↔B
1
0
0
1













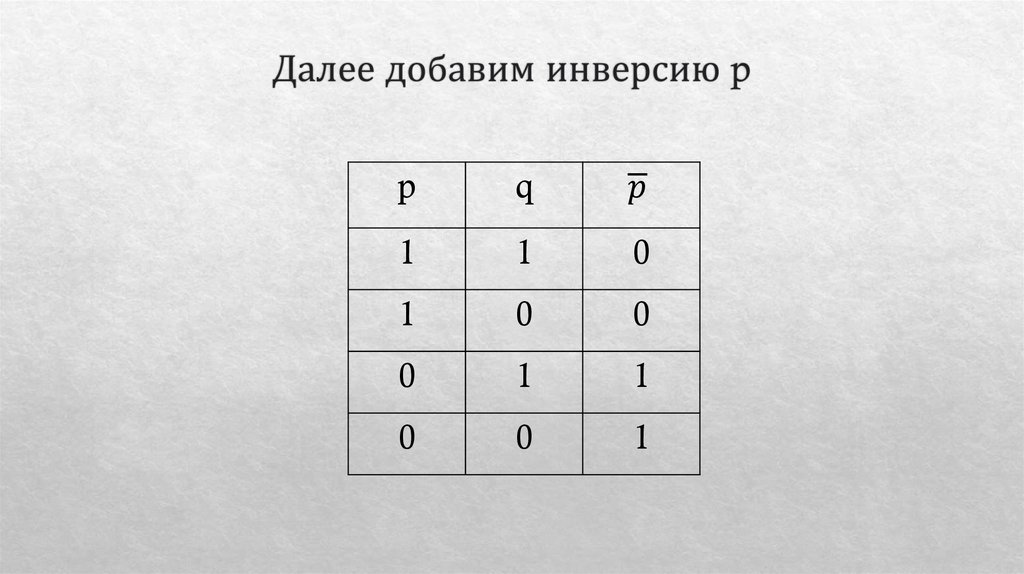
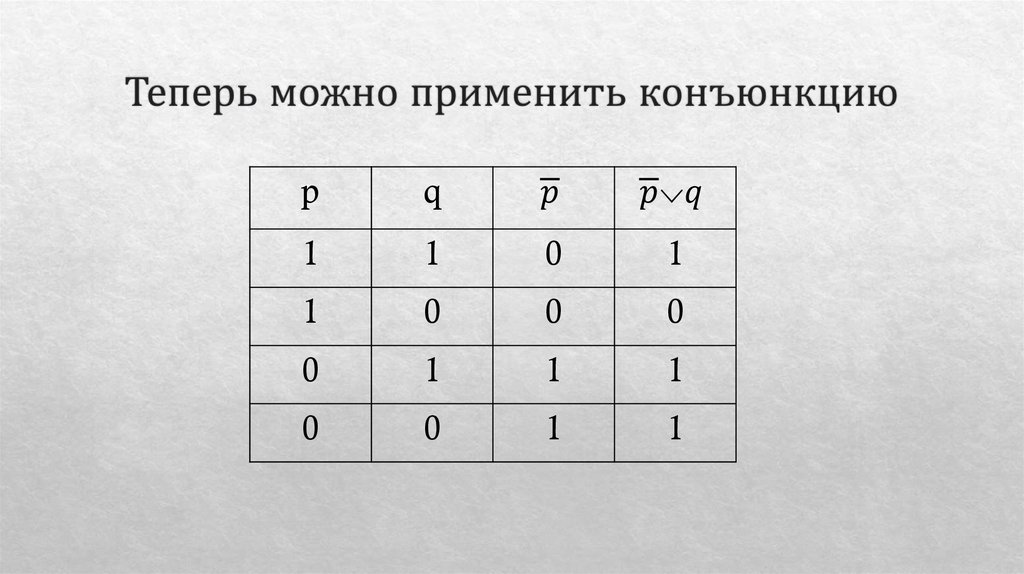
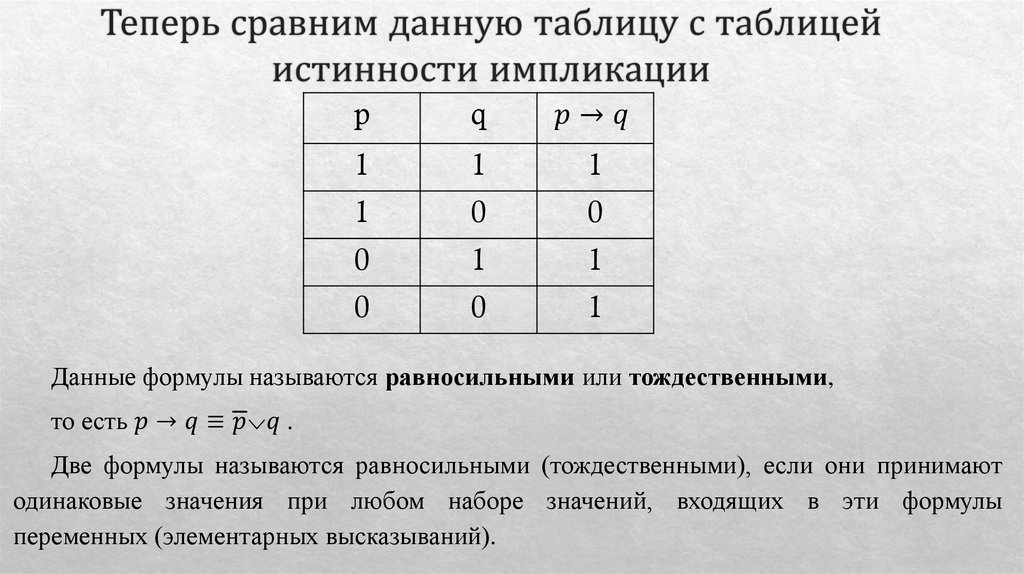

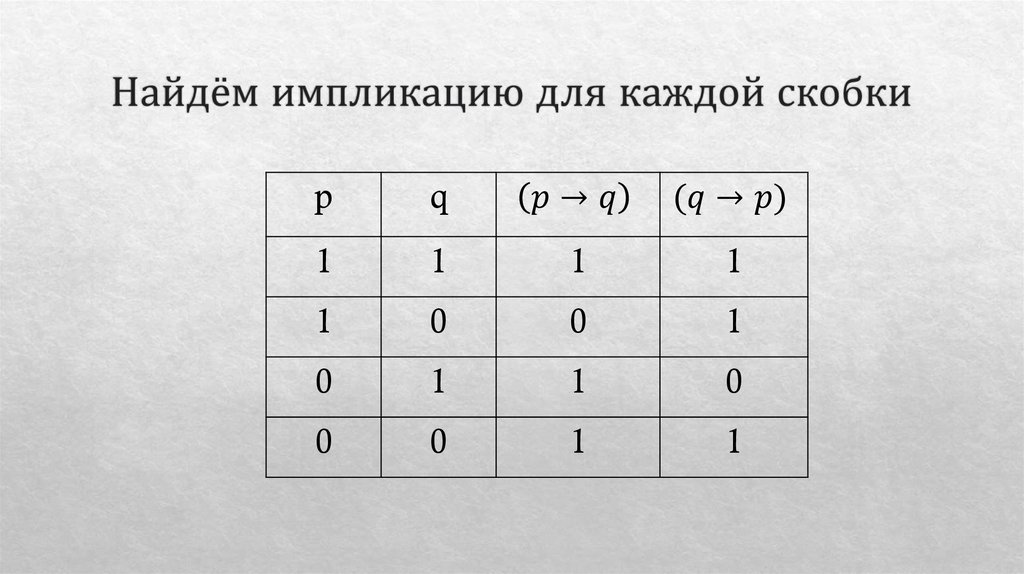
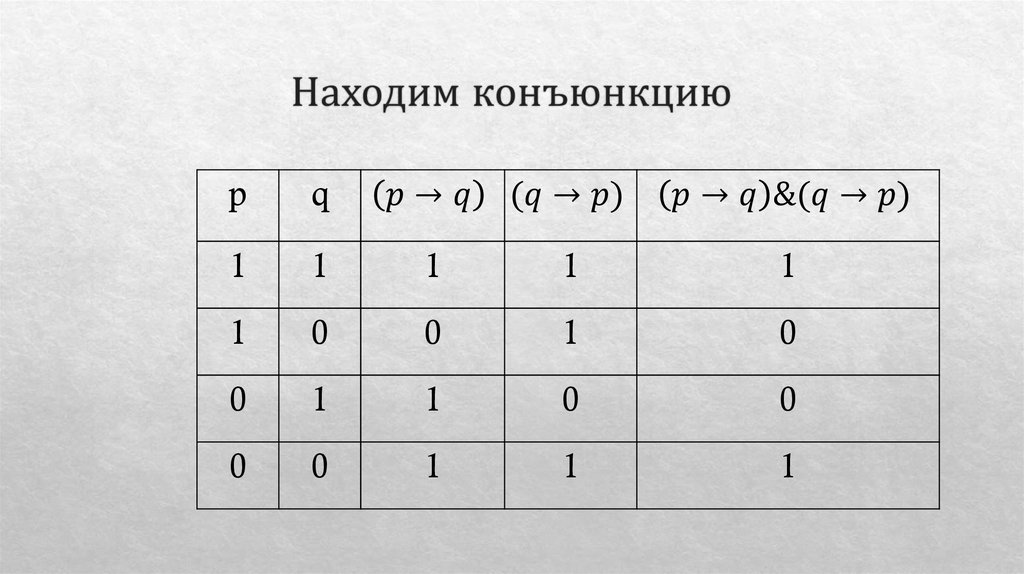
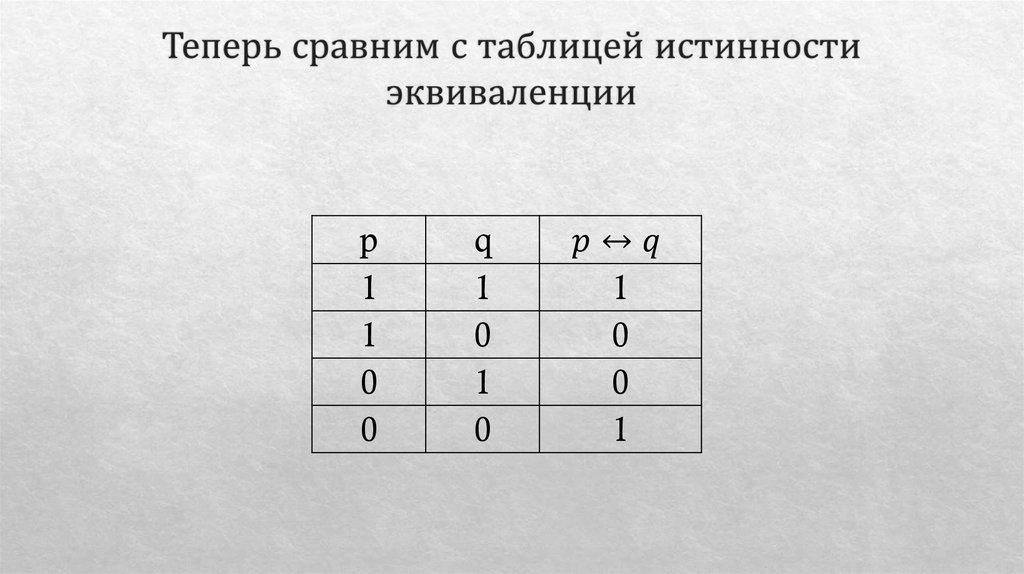




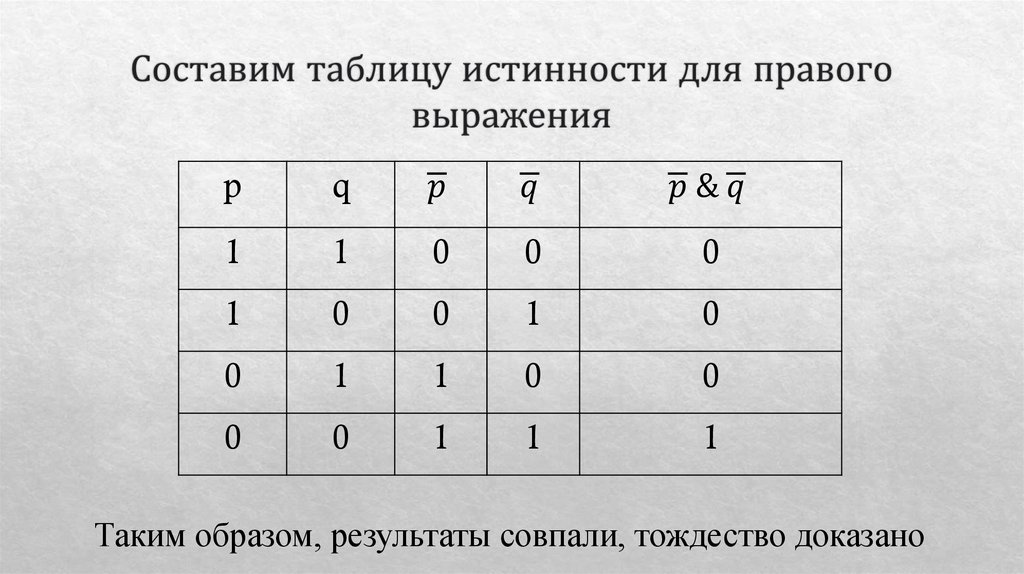


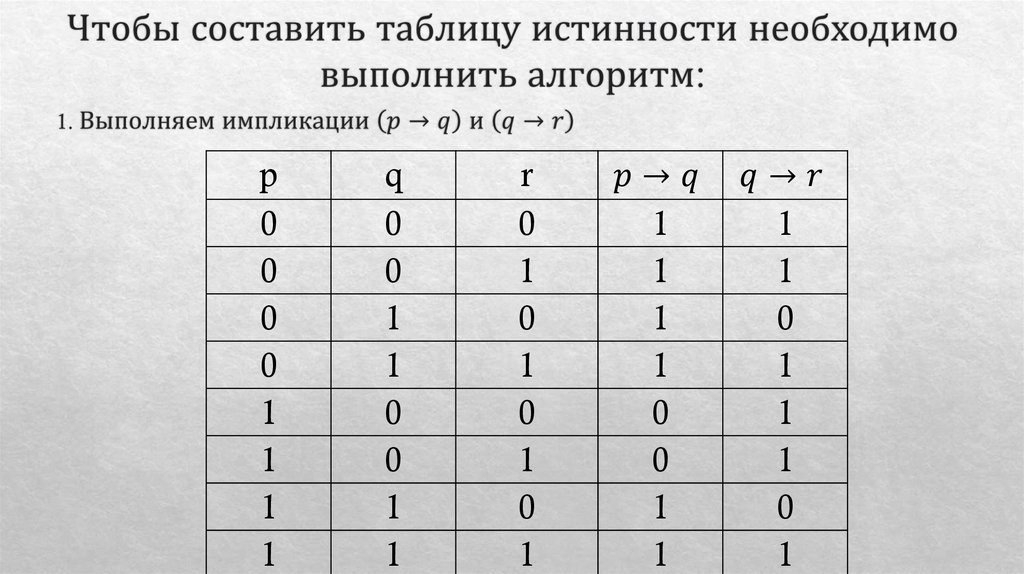
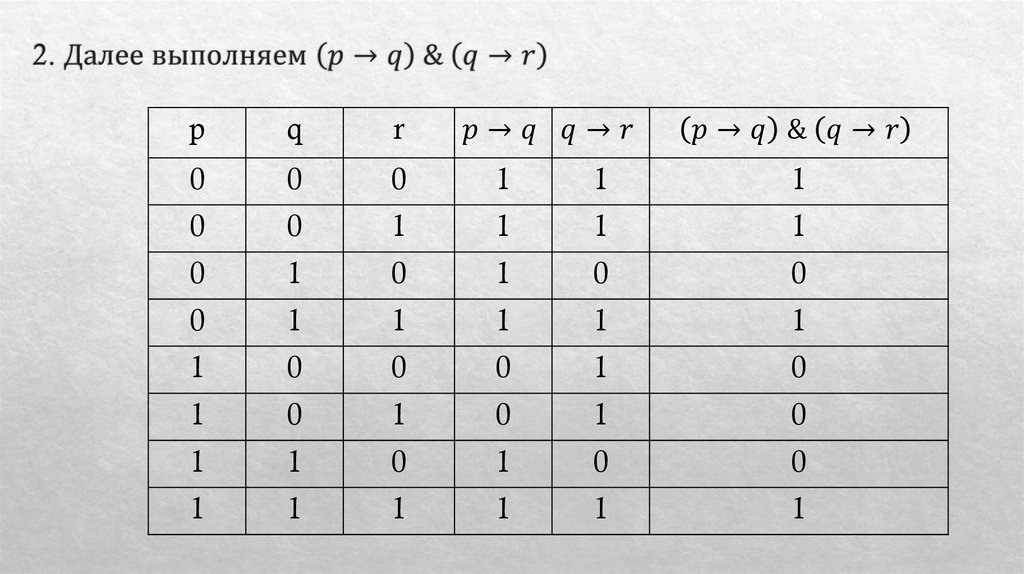
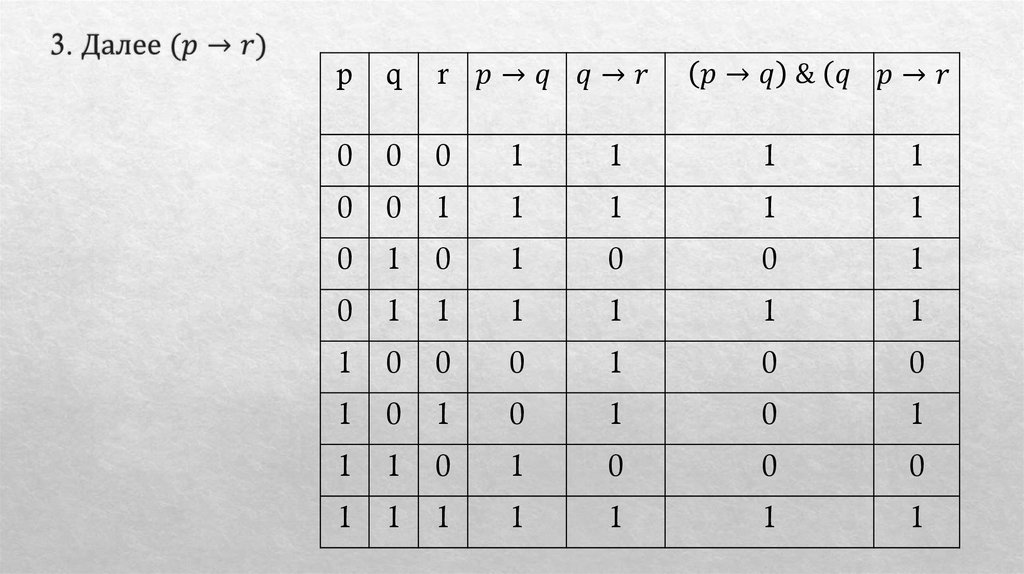
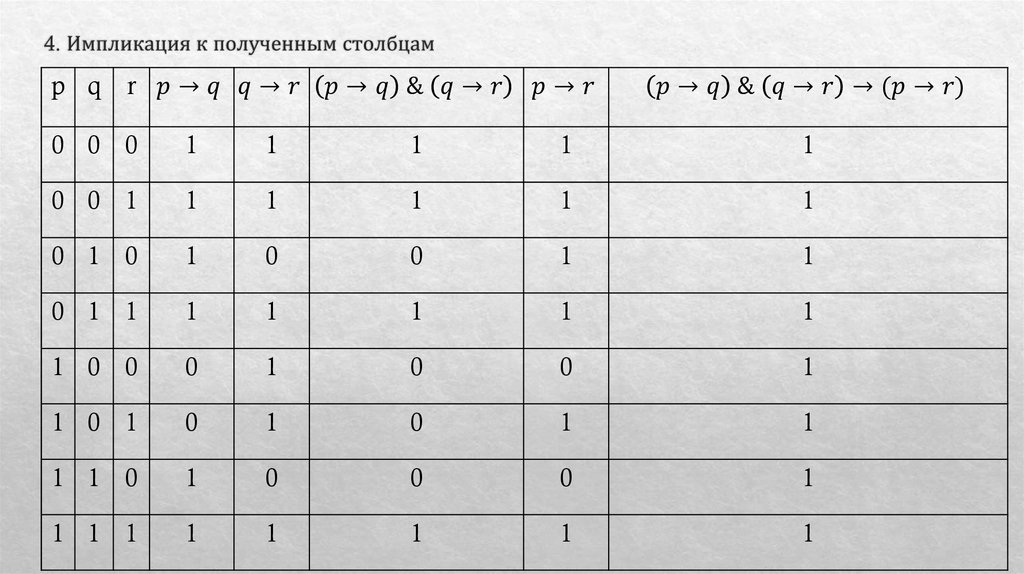






 Математика
Математика








