Область определения предиката. Множество истинности предиката

Пример. Даны два предиката P: «5х – 6 < 3x»; Q: «2 < x ≤ 8». Найти множества истинности предикатов: ¯(P(x)), ¯(Q(x)), P(x) &

ПРИМЕР. Предикат Р(х,у): «х:у», определенный на множестве N. Применение кванторных операций к предикату Р(х, у) приводит к

Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание.

Построение отрицаний к предикатам, содержащим кванторные операции

Пример. Рассмотрим на множестве Х = {-2, -1, 0, 1, 2, 3, 4, 5, …,9} предикат А(х): «х – натуральное число»

Пример. На множестве Х = {-2, -1, 0, 1, 2, … , 10} заданы предикаты А(х): «2х - 1 < 3» и В(х): «х + 2х = 0». Получить предикат

1.54M

Категория: $Математика$ Математика

Похожие презентации:

Логика предикатов

Элементы математической логики. Операции над предикатами

Предикаты. Понятие предиката

Логика предикатов

Исчисление предикатов

Предикат. Логические операции над предикатами

Предикаты

1. Предикаты

ПРЕДИКАТЫ

2. Понятие предиката

ПОНЯТИЕ ПРЕДИКАТА
• Определение 1. Предложение, содержащее переменные,
которые при замене их на возможные значения становятся
высказываниями, называются предикатом или
высказывательной формой.
• Определение 2. Предикат – логическая функция от некоторого
числа предметных элементов, которая определяет свойства
объекта или отношения между объектами.

3. Понятие предиката

ПОНЯТИЕ ПРЕДИКАТА
Субъект – это то, о чем что-то утверждается в
высказывании; предикат – это то, что утверждается о
субъекте.
Например, в высказывании «7 – простое число», «7» –
субъект, «простое число» – предикат. Это высказывание
утверждает, что «7» обладает свойством «быть простым
числом».
Одноместным предикатом Р(х) называется произвольная
функция переменного х, определенная на множестве М и
принимающая значения из множества {1,0}.

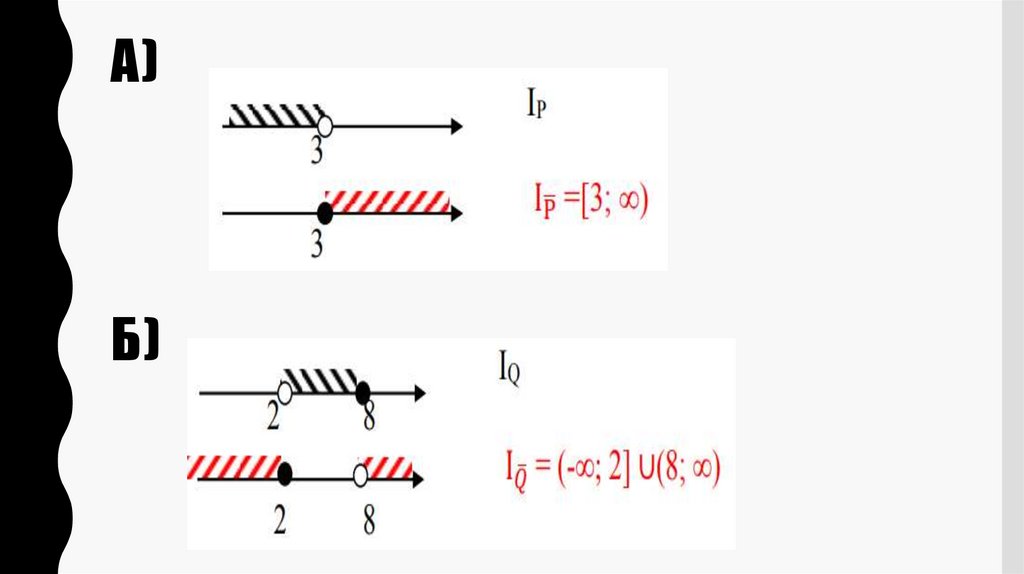
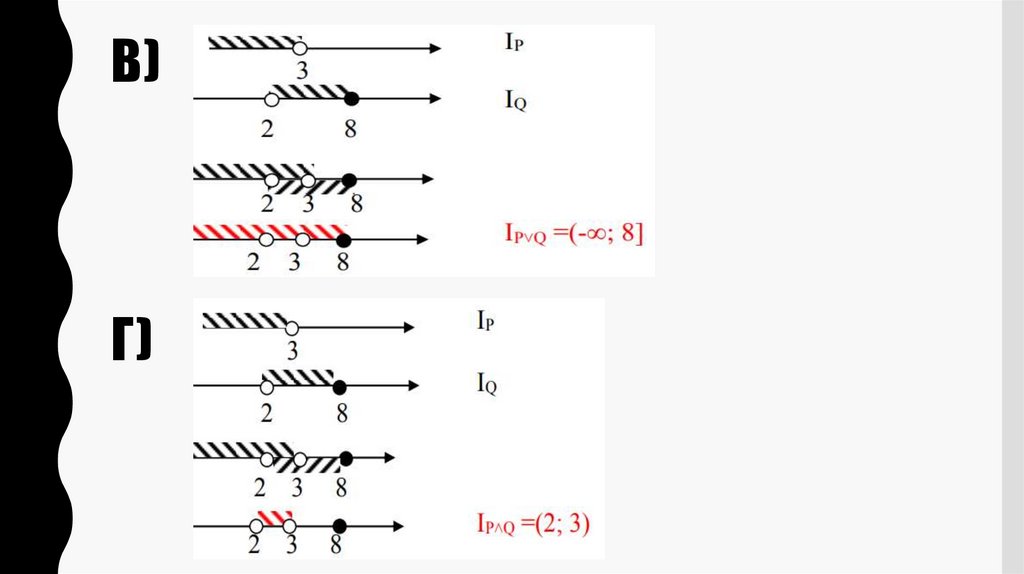
4. Область определения предиката. Множество истинности предиката

ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ПРЕДИКАТА.
МНОЖЕСТВО ИСТИННОСТИ ПРЕДИКАТА
• Множество М, на котором определен предикат Р(х),
называется областью определения предиката.
• Множество всех элементов x ∈ M, при которых предикат
принимает значение «истина», называется множеством
истинности предиката Р(х) , то есть множество истинности
предиката Р(х) – это множество

English Русский Правила