Похожие презентации:
Графы
1.
Гамильтонов цикл.2.
Множество внешней устойчивости графаМножество внешней устойчивости (D) (доминирующее множество)
– множество вершин, для которых выполняется одно из следующих
правил:
1). Любая вершина входит в это множество
2) Либо вершина не входит в это множество, но из этой вершины есть
дуга в данное множество.
Число внешней устойчивости (β) (число доминирования)– это
наименьшая мощность из всех множеств внешней устойчивости.
3.
Множество внешней устойчивости графа1. Для графа составляется матрица смежности
2. Матрица смежности дополняется единицами (1) по главной диагонали
3. Находим такую наименьшую совокупность строк полученной
матрицы, чтобы каждый ее столбец имел единицу, по крайней мере, в
одной из строк найденной совокупности.
4.
Множество внешней устойчивости графа5.
Множество внешней устойчивости графа6.
Множество внутренней устойчивости графаМножество внутренней устойчивости графа (независимое
множество)– это множество несмежных вершин
Максимальным множеством внутренней устойчивости называется
внутренне устойчивое множество, добавление любой вершины к
которому, делает это множество неустойчивым.
Числом внутренней устойчивости (α) (вершинным числом
независимости) называется число, равное наибольшей мощности
максимального внутренне устойчивого множества
{ A, E}, {B, D}, {B, E}, {C , D}, {C , E}
можно ли расставить на шахматной доске восемь ферзей
так, чтобы ни один из них не находился под ударом другого.
7.
Множество внешней устойчивости графаИначе в множестве V \ S найдется вершина,
не смежная ни с одной вершиной из S
8.
Клика графаантипод понятия независимого множества графа
Кликой графа называется множество вершин, которое
порождает полный подграф.
Клика, не являющаяся подмножеством никакой другой
клики (с большим числом вершин), называется
максимальной, а клика с наибольшим числом вершин –
наибольшей. Число вершин в наибольшей клике графа G
называется его кликовым числом (или плотностью).
9.
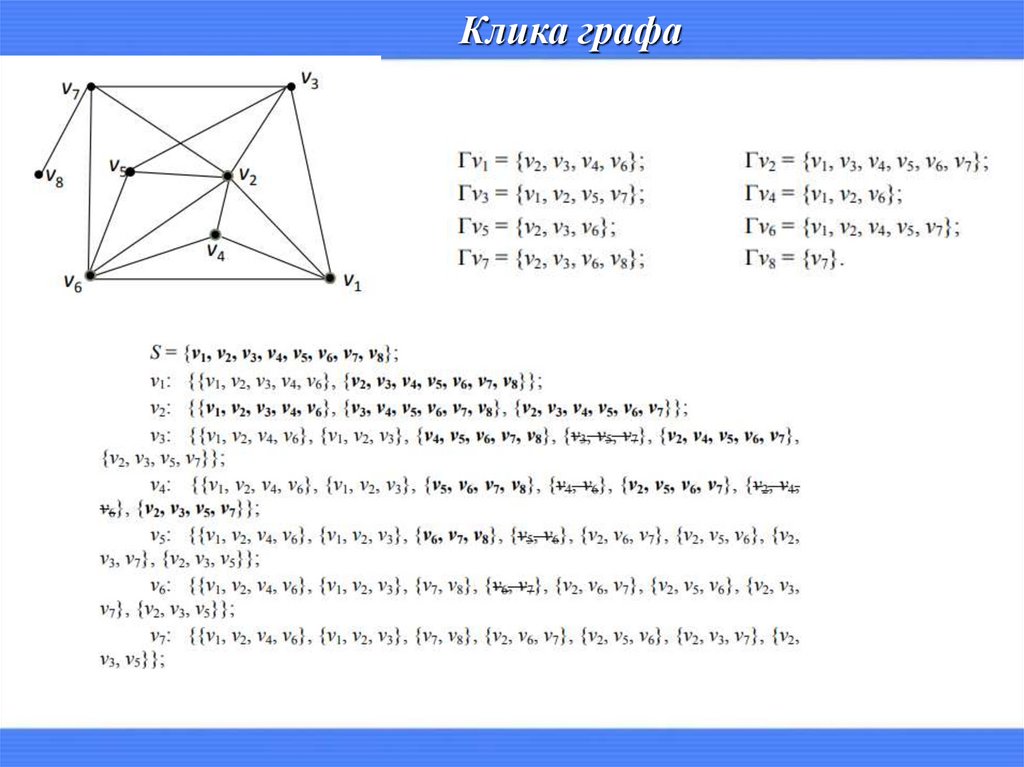
Клика графа10.
Клика графаЗадача нахождения клик графа и задача
нахождения независимых множеств в некотором
графе являются двойственными по отношению
друг к другу
11.
Вершинные покрытия графабудем считать, что вершина покрывает инцидентные ей
ребра, а ребро покрывает инцидентные ему вершины.
Множество вершин графа, покрывающих все его ребра,
называется вершинным покрытием графа.
Вершинное покрытие графа называется минимальным, если
оно не содержит покрытия с меньшим числом вершин, и
наименьшим, если в нем наименьшее число вершин (среди
всех покрытий этого графа). Число вершин в наименьшем
покрытии графа G называется числом вершинного покрытия
12.
Вершинные покрытия графа13.
Паросочетания и реберные покрытияМножество попарно не смежных ребер графа
называется независимым множеством ребер или
паросочетанием.
14.
Паросочетания и реберные покрытия15.
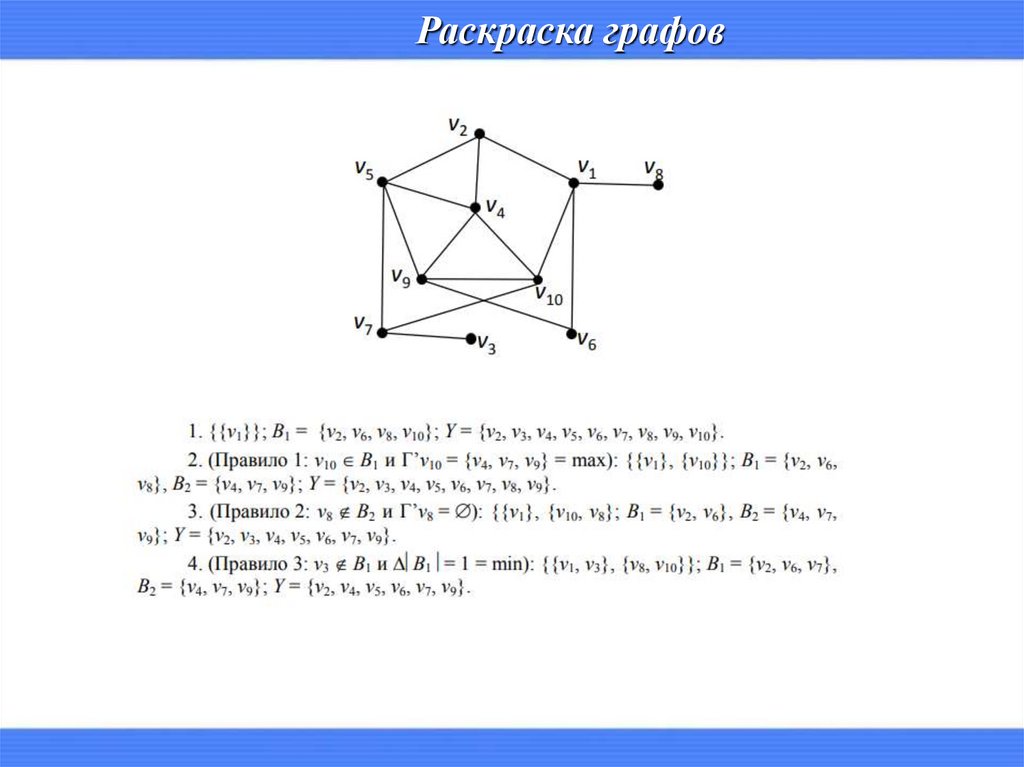
Раскраска графов16.
Раскраска графовнезависимые множества
Кратчайшее покрытие столбцов матрицы






























 Математика
Математика








