элементы комбинаторики

1.

Элементы
комбинаторики

2.

Повторение:
1. Что называется средним арифметическим ряда чисел?
Частное от деления суммы этих чисел на число слагаемых
Среднее арифметическое ряда находят тогда, когда хотят
определить среднее значение для некоторого ряда данных
Задача: При изучении учебной нагрузки студентов выделили группу из 12
первокурсников. Их попросили отметить в определенный день время (в
минутах), затраченное на выполнение домашнего задания по математике.
Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
Имея этот ряд данных, можно определить, сколько минут в среднем
затратили студенты на выполнение домашнего задания по математике.
Чему равно это время?
23+ 18+ 25+ 20+ 25+ 25+ 32+ 37+ 34+ 26+ 34+ 25 324
=
=27
12
12
Результат 27 — среднее арифметическое рассматриваемого ряда

3.

Повторение:
2. Что называется размахом ряда чисел?
Разность между наибольшим и наименьшим из ряда чисел
Размах ряда находят тогда, когда хотят определить, как
велик разброс данных в ряду
Задача: В течении суток отмечали каждый час температуру воздуха в
городе. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
Имея этот ряд данных, можно определить размах ряда, характеризующий
колебание температуры воздуха в течении этих суток. Чему равен этот
размах?
37 — наибольшее число в ряде
18 — наименьшее число в ряде
37-18=19
Результат 9 - размах ряда, характеризующий колебание температуры

4.

Повторение:
3. Что называется модой ряда чисел?
Наиболее часто встречающееся число в ряде
Моду ряда находят тогда, когда хотят выяснить некоторые
типичные показатели
Ряд может иметь моду в ряду, а может её и не быть совсем
В нашем ряде данных:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
Чему равна мода и почему?
Число 25 - мода ряда, так она встречается в нем четыре раза
Дан ряд:
69, 68, 66, 70, 67, 71, 74, 63, 73, 72
Есть ли в данном ряду мода?

5.

Повторение:
Задача: На предприятии проводят учет деталей, изготовленных за смену
рабочими одной бригады, получили такой ряд данных:
36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 37, 39, 38, 38, 36, 39, 36,39
Найдите для данного ряда среднее арифметическое, размах и моду.
число
35
36
37
38
39
Упорядоченный ряд
кол-во
35⋅2+ 36⋅2+ 37⋅4+ 38⋅3+ 39⋅4 776
=
=37
21
21
39-35=4 — размах ряда
среднее арифметическое ряда
36 — мода ряда
Задание:
Найдите среднее арифметическое, размах и моду ряда
1) 32, 26, 18, 26, 15, 21, 26;
2) 21, 18, 25, 18, 17;
3) -21, -33, -35, -19, -20, -22;
4) -4, 0, -6, 4, 6, 8, -12.

6.

Повторение:
4. Что называется медианой ряда чисел?
В таблице показан расход электроэнергии в январе жильцами девяти квартир:
Номер квартиры
1
2
3
4
5
6
7
8
9
Расход, кВт*ч
85
64
78
93
72
91
72
75
82
Получается следующий упорядоченный ряд:
64, 72, 72, 75, 78, 82, 85, 91, 93
Число 78 — серединное или медиана упорядоченного ряда
78+ 82
=¿ квартиры:
В таблицу добавили показания еще одной
2
Номер квартиры
1
2
3
4
5
6
7
8
9
10
Расход, кВт*ч
85
64
78
93
72
91
72
75
82
88
Получается следующий упорядоченный ряд:
64, 72, 72, 75, 78, 82, 85, 88, 91, 93
Числа 78 и 82 — серединные упорядоченного ряда
Медиана равна
медианой
78+ 82
=80
, 80 2
не является членом ряда, но является

7.

Повторение:
4. Что называется медианой ряда чисел?
Медианой упорядоченного ряда чисел с нечетным числом членов
называется число, записанное посередине, а четным числом
членов называется среднее арифметическое чисел, записанных
посередине.
Медианой произвольного ряда чисел называется медиана
соответствующего упорядоченного ряда
Задание:
Найдите медиану ряда:
1) 32, 26, 18, 26, 15, 21, 26;
2) 21, 18, 25, 18, 17;
3) -21, -33, -35, -19, -20, -22;
4) -4, 0, -6, 4, 6, 8, -12.

8.

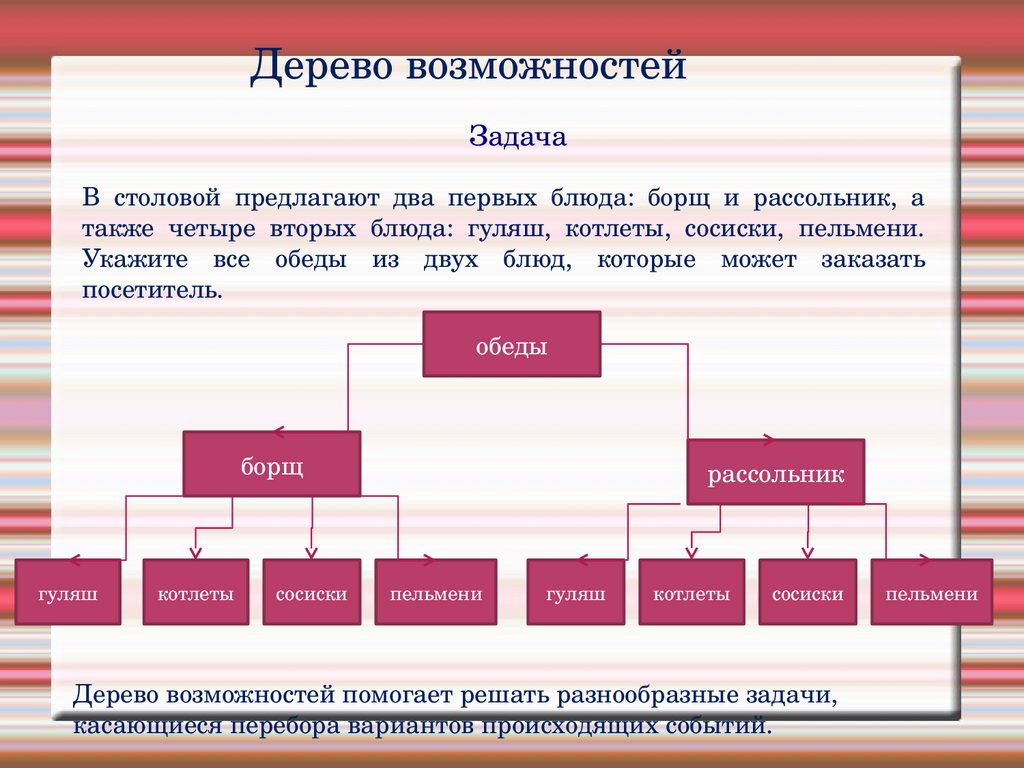
Дерево возможностей
Задача
В столовой предлагают два первых блюда: борщ и рассольник, а
также четыре вторых блюда: гуляш, котлеты, сосиски, пельмени.
Укажите все обеды из двух блюд, которые может заказать
посетитель.
обеды
борщ
гуляш
котлеты
сосиски
рассольник
пельмени
гуляш
котлеты
сосиски
Дерево возможностей помогает решать разнообразные задачи,
касающиеся перебора вариантов происходящих событий.
пельмени

9.

В этой задаче речь идёт о комбинациях объектов.
Такие задачи называются комбинаторными.
Комбинаторика – это раздел математики, в
котором изучаются вопросы о том, сколько
различных комбинаций, подчинённых тем
или иным условиям, можно составить из
заданных объектов.
Термин «комбинаторика» происходит от латинского
слова
combina - сочетать, соединять.
Комбинаторика занимается различного рода
сочетаниями
(соединениями), которые можно образовать из
элементов некоторого конечного множества.

10.

Немного истории
С комбинаторными задачами люди
сталкивались с глубокой
древности. В
Древнем Китае увлекались
составлением математических
головоломок
(магические квадраты), в Древней
Греции составляли геометрические
головоломки на разрезание и
складывание фигур (до наших дней
дошла головоломка «Пифагор»).
Термин «комбинаторика» был
Готфрид Вильгельм фон Лейбниц
введён в математический обиход
(1646 - 1716 гг.)
немецкий философ и математик.
Лейбницем.

11.

Немного истории
Леонард Эйлер
рассматривал задачи о
разбиении чисел, о
паросочетаниях, о
циклических расстановках,
о построении магических и
латинских квадратов.
Леонард Эйлер
(1707 — 1783г.г.)
выдающийся математик,
родился в Швейцарии, жил и работал в
России

12.

Немного истории
Комбинаторика – ветвь математики , изучающая комбинации
перестановки предметов .Еще комбинаторику можно понимать как
перебор возможных вариантов.
Комбинаторика возникла в 17 веке. Комбинаторные навыки оказались
полезными в часы досуга. В таких играх как нарды, карты, шашки,
шахматы приходилось рассматривать различные сочетания фигур и
выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и
умел избегать проигрышные.
Еще с давних пор дипломаты стремясь к тайне переписке, изобретали
сложные шифры, а секретные службы пытались эти шифры разгадать.
Методы комбинаторики находят широкое применение в физике, химии,
биологии, экономике и др. областях.
Выбором объектов и их расположением приходится заниматься чуть ли
не во всех областях человеческой деятельности – конструктору, учёномугенетику, агроному, составителю кодов, лотерей, химику, комбинаторные
задачи применяются при игре в шашки, шахматы, при подсчёте
вариантов в теории вероятностей и т.д.

13.

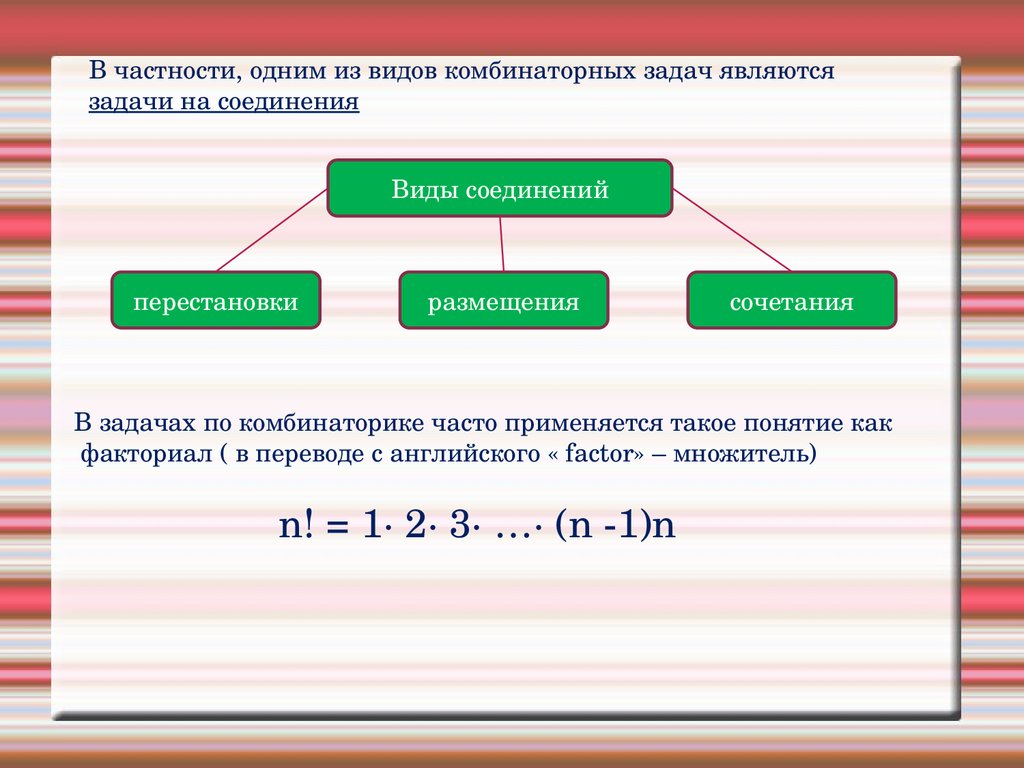
В частности, одним из видов комбинаторных задач являются
задачи на соединения
Виды соединений
перестановки
размещения
сочетания
В задачах по комбинаторике часто применяется такое понятие как
факториал ( в переводе с английского « factor» – множитель)
n! = 1· 2· 3· …· (n -1)n

14.

Перестановки.
Опр. Перестановкой из n элементов называется последовательность,
состоящая из всех элементов некоторого n-элементного множества,
причем число элементов этой последовательности равно n.
Формула (число размещений «из эн по эм»):
Рn n!
Задача: В расписании сессии 3 экзамена (история, геометрия,
алгебра). Сколько может быть вариантов расписаний?
Решение. (обратить внимание на его оформление!)
Основное множество: {история, геометрия, алгебра}
n 3
Соединение – вариант расписания сессии
Проверим, важен ли порядок:
{история, геометрия, алгебра} и {геометрия, история, алгебра} –
варианты расписания сессии для разных групп порядок важен
это последовательность это перестановка из трех элементов.
Р3 3! 6
Ответ: 6 вариантов

15.

Размещения
Опр. Размещением из n элементов по m ( m ≤ n) называется
последовательность, состоящая из m различных элементов некоторого n
элементного множества.
Формула (число размещений «из эн по эм»):
n!
A
( n m )!
m
n
Задача: Сколько существует двузначных чисел, в которых цифра
десятков и цифра единиц различны и нечетны?
Решение (обратить внимание на его оформление!)
Основное множество: {1, 3, 5, 7, 9} – нечетные
цифры
Соединение – двузначное число m
2
n 5
Проверим, важен ли порядок: 13 31 - разные двузначные числа
порядок важен это последовательность это размещение «из пяти
по два».
5!
A
4 5 20 двузначных чисел
( 5 2 )!
2
5
Ответ: 20 чисел.

16.

Сочетания
Опр. Сочетанием из n элементов по m ( m ≤ n) называется mэлементное подмножество некоторого n элементного множества.
Формула (число размещений «из эн по эм»):
C nm
n!
( n m )! m!
Задача: Сколькими способами можно составить букет из 3 цветов,
если в вашем распоряжении 5 цветов: мак, роза, тюльпан, лилия,
гвоздика?
Решение. (обратить внимание на его оформление!)
Основное множество: {мак, роза, тюльпан, лилия,n 5
гвоздика}
Соединение – букет из трех цветков m 3
Проверим, важен ли порядок:
{тюльпан, лилия, гвоздика} и {лилия, тюльпан, гвоздика} – один и тот же
букет порядок неважен это подмножество это сочетание «из пяти
по три».
C53
5!
4 5
10
( 5 3 )! 3!
2
Ответ: 10 букетов