Некоторые задачи на графах и графы с особыми свойствами. Тема 3.2

1. Раздел 3: Основы теории графов

Тема 3.2. Некоторые задачи на графах и графы с
особыми свойствами
Преподаватель ОЯТЦ ИЯТШ
Егорова О.В.

2. План лекций

2
План лекций
задача сравнения графов
понятие эйлерова графа и алгоритмы поиска
эйлерова цикла в графе
понятие взвешенных орграфов и алгоритмы поиска
экстремальных путей в них
полные и k-дольные графы
деревья

3. Задача сравнения графов

3
Задача сравнения графов
один и тот же граф можно по-разному изобразить графически
возникает задача: по имеющимся изображениям графов, содержащих одинаковое
количество ребер и имеющих один порядок, установить разные это графы или один
и тот же
для разрешения подобной задачи используется понятие ИЗОМОРФИЗМА
Графы G1 = (V1, E1) и G2 = (V2, E2) изоморфны, если существует взаимно
однозначное соответствие между множествами вершин V1 и V2, сохраняющее
смежность вершин
Обозначение: G1 G2 или G1 G2
Пример:
!!!! Изоморфизм графов есть
отношение эквивалентности
(оно рефлексивно, симметрично и
транзитивно)
изоморфные графы

4. Изоморфизм графов

4
Изоморфизм графов
Изоморфные графы отличаются друг от друга только
порядком нумерации вершин или ребер
матрицы смежности двух изоморфных графов могут быть получены одна из
другой перестановкой строк и столбцов
чтобы узнать, являются ли два графа изоморфными, нужно произвести все
возможные перестановки строк и столбцов матрицы смежности одного из
графов
если после какой-нибудь перестановки получится матрица смежности второго
графа, то эти графы изоморфны
чтобы убедиться, что графы неизоморфны, надо выполнить все n! возможных
перестановок строк и столбцов (n- число вершин графа)
можно сократить количество перестановок, если использовать
инварианты (некоторые числовые характеристики графа G,
принимающие одно и тоже значение для любого графа, изоморфного G)
следует учитывать, что не известен полный набора инвариантов,
который бы определял вид любого графа с точностью до
изоморфизма

5. Изоморфизм графов

5
Изоморфизм графов
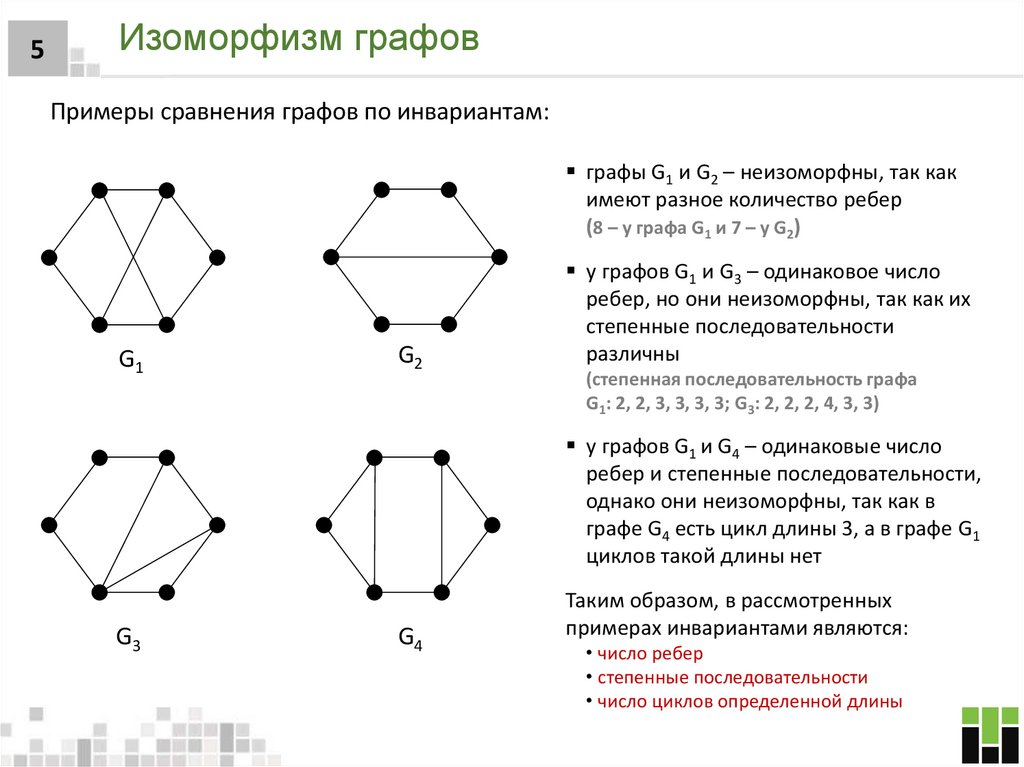
Примеры сравнения графов по инвариантам:
графы G1 и G2 – неизоморфны, так как
имеют разное количество ребер
(8 – у графа G1 и 7 – у G2)
G1
G2
у графов G1 и G3 – одинаковое число
ребер, но они неизоморфны, так как их
степенные последовательности
различны
(степенная последовательность графа
G1: 2, 2, 3, 3, 3, 3; G3: 2, 2, 2, 4, 3, 3)
у графов G1 и G4 – одинаковые число
ребер и степенные последовательности,
однако они неизоморфны, так как в
графе G4 есть цикл длины 3, а в графе G1
циклов такой длины нет
G3
G4
Таким образом, в рассмотренных
примерах инвариантами являются:
• число ребер
• степенные последовательности
• число циклов определенной длины

6. Изоморфизм графов

6
Изоморфизм графов
Примеры используемых инвариантов:
число вершин и ребер
степенная последовательность (или вектор степеней графа)
вектор степеней 2-го порядка – вектор, каждый элемент которого
представляет собой список степеней вершин, смежных с данной
диаметр графа
индекс Винера:
r( v ,v )
i , j , i j
индекс Рандича: r
( vi , v j ) V
i
j
1
deg (vi ) deg (v j )
определитель матрицы смежности
число компонент связности графа
и др.
r(vi,vj) – расстояние между вершинами vi и
vj
deg(vi),(vj)) – степени вершинами vi и vj

7. Изоморфизм графов

7
Изоморфизм графов
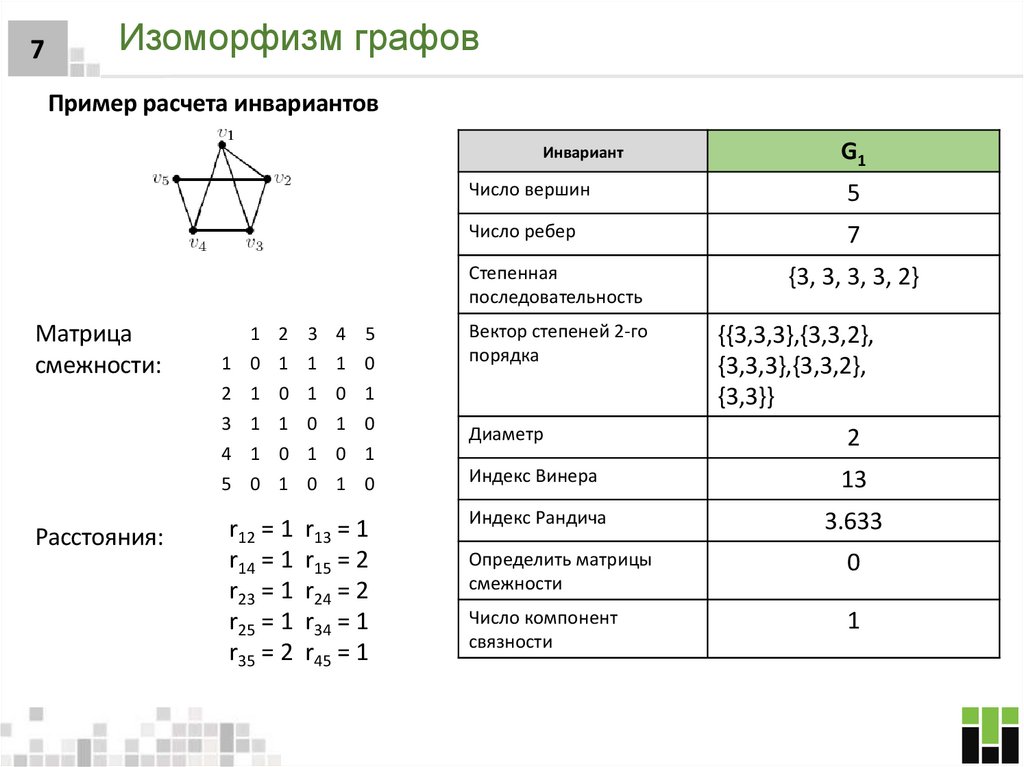
Пример расчета инвариантов
Инвариант
Число вершин
5
Число ребер
7
Степенная
последовательность
Матрица
смежности:
Расстояния:
1
2
3
4
5
1
0
1
1
1
0
2
1
0
1
0
1
3
1
1
0
1
0
4
1
0
1
0
1
5
0
1
0
1
0
r12 = 1 r13 = 1
r14 = 1 r15 = 2
r23 = 1 r24 = 2
r25 = 1 r34 = 1
r35 = 2 r45 = 1
G1
Вектор степеней 2-го
порядка
{3, 3, 3, 3, 2}
{{3,3,3},{3,3,2},
{3,3,3},{3,3,2},
{3,3}}
Диаметр
2
Индекс Винера
13
Индекс Рандича
3.633
Определить матрицы
смежности
0
Число компонент
связности
1

8. Изоморфизм графов

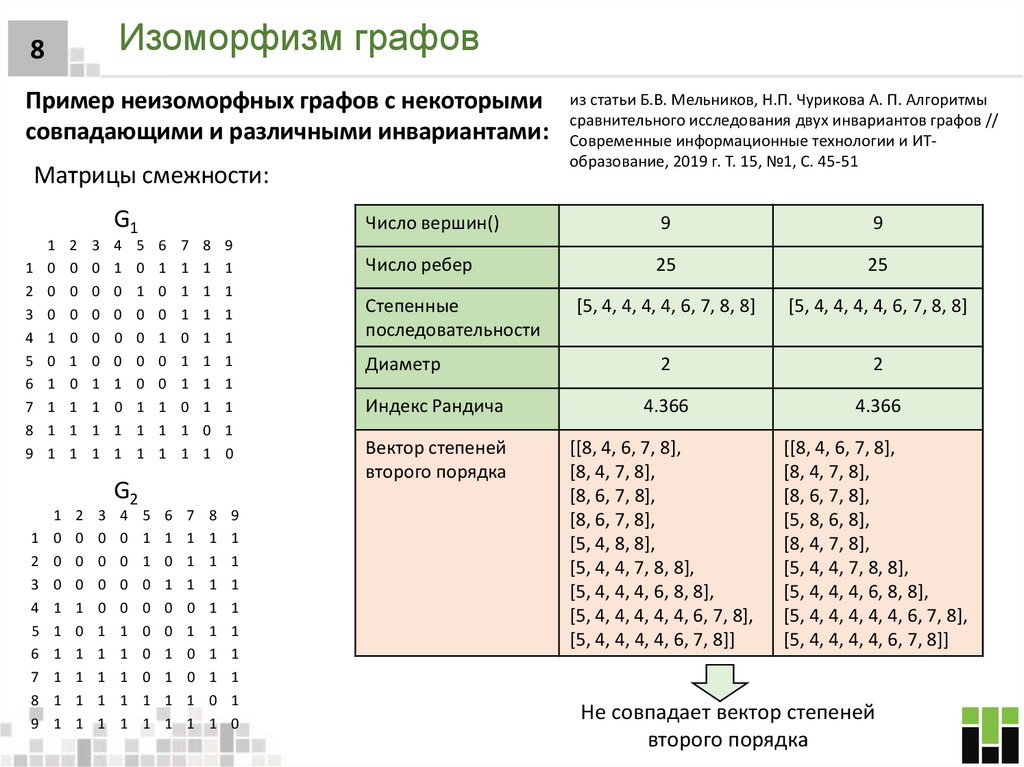
8
Пример неизоморфных графов с некоторыми
совпадающими и различными инвариантами:
Матрицы смежности:
G1
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
0
0
0
1
0
1
1
1
1
1
0
0
0
1
1
1
1
1
1
2
0
0
0
0
1
0
1
1
1
2
0
0
0
1
0
1
1
1
1
3
0
0
0
0
0
1
1
1
1
3
0
0
0
0
1
1
1
1
1
4
1
0
0
0
0
1
0
1
1
5
0
1
0
0
0
0
1
1
1
G2
4
0
0
0
0
1
1
1
1
1
5
1
1
0
0
0
0
0
1
1
6
1
0
0
1
0
0
1
1
1
7
1
1
1
0
1
1
0
1
1
8
1
1
1
1
1
1
1
0
1
9
1
1
1
1
1
1
1
1
0
6
1
0
1
0
0
1
1
1
1
7
1
1
1
0
1
0
0
1
1
8
1
1
1
1
1
1
1
0
1
9
1
1
1
1
1
1
1
1
0
из статьи Б.В. Мельников, Н.П. Чурикова А. П. Алгоритмы
сравнительного исследования двух инвариантов графов //
Современные информационные технологии и ИТобразование, 2019 г. Т. 15, №1, С. 45-51
Число вершин()
9
9
Число ребер
25
25
[5, 4, 4, 4, 4, 6, 7, 8, 8]
[5, 4, 4, 4, 4, 6, 7, 8, 8]
2
2
Индекс Рандича
4.366
4.366
Вектор степеней
второго порядка
[[8, 4, 6, 7, 8],
[8, 4, 7, 8],
[8, 6, 7, 8],
[8, 6, 7, 8],
[5, 4, 8, 8],
[5, 4, 4, 7, 8, 8],
[5, 4, 4, 4, 6, 8, 8],
[5, 4, 4, 4, 4, 4, 6, 7, 8],
[5, 4, 4, 4, 4, 6, 7, 8]]
[[8, 4, 6, 7, 8],
[8, 4, 7, 8],
[8, 6, 7, 8],
[5, 8, 6, 8],
[8, 4, 7, 8],
[5, 4, 4, 7, 8, 8],
[5, 4, 4, 4, 6, 8, 8],
[5, 4, 4, 4, 4, 4, 6, 7, 8],
[5, 4, 4, 4, 4, 6, 7, 8]]
Степенные
последовательности
Диаметр
Не совпадает вектор степеней
второго порядка

9. Изоморфизм графов

9
Изоморфизм графов
анализ графов на изоморфность целесообразно начинать со сравнения
значений инвариантов
при совпадении инвариантов переходить к перебору допустимых вариантов
нумерации вершин
(примеры инвариантов графа: число вершин и ребер, степенные последовательности,
количество циклов и т.п.)
Алгоритм проверки на изоморфность неорграфов:
(заданных матрицами смежности)
сравниваются размерности матриц, они должны совпадать
считается количество единиц выше главной диагонали и на
главной диагонали (это количество должно совпадать)
далее матрица одного из сравниваемых графов приводится к виду,
в котором она будет совпадать с матрицей второго сравниваемого
графа (путем перестановки строк и столбцов)
если после n! возможных перестановок строк и столбцов (n- число
вершин графа) матрицы не совпали, то графы неизоморфны

10. Понятие эйлерова графа

10
Понятие эйлерова графа
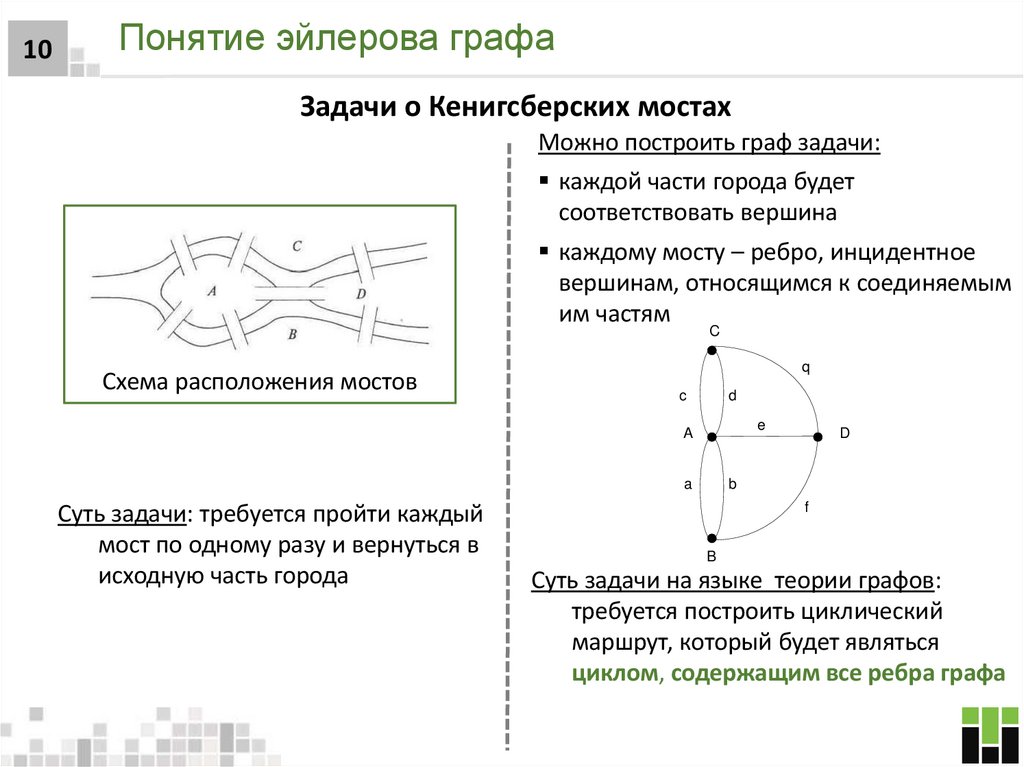
Задачи о Кенигсберских мостах
Можно построить граф задачи:
каждой части города будет
соответствовать вершина
каждому мосту – ребро, инцидентное
вершинам, относящимся к соединяемым
им частям
C
Схема расположения мостов
q
c
d
e
A
a
Суть задачи: требуется пройти каждый
мост по одному разу и вернуться в
исходную часть города
D
b
f
B
Суть задачи на языке теории графов:
требуется построить циклический
маршрут, который будет являться
циклом, содержащим все ребра графа

11. Понятие эйлерова графа

11
Понятие эйлерова графа
Эйлеровым циклом называется цикл, проходящий по каждому ребру
графа G=(V, E) ровно один раз
(цикл включает в себя все ребра и вершины графа G)
Эйлеровым графом называется граф, имеющий эйлеровы циклы
(плоский эйлеров граф можно нарисовать, не
отрываясь от бумаги, начиная с некоторой
вершины и заканчивая в ней же)

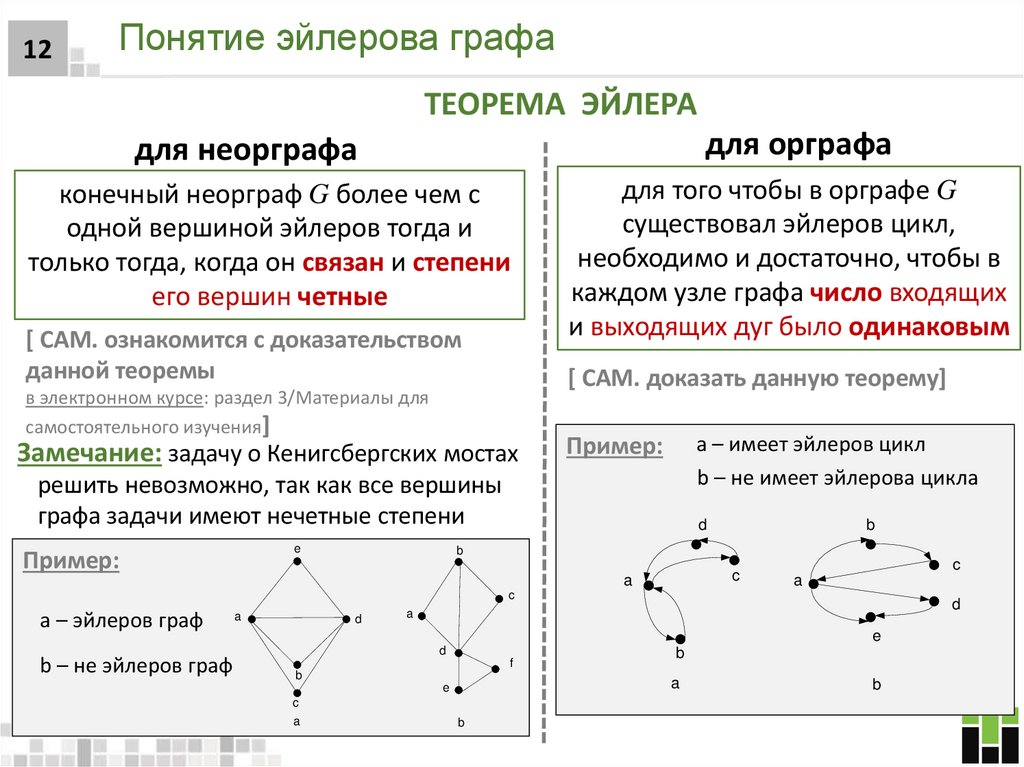
12. Понятие эйлерова графа

12
Понятие эйлерова графа
ТЕОРЕМА ЭЙЛЕРА
для орграфа
для неорграфа
конечный неорграф G более чем с
одной вершиной эйлеров тогда и
только тогда, когда он связан и степени
его вершин четные
[ САМ. ознакомится с доказательством
данной теоремы
для того чтобы в орграфе G
существовал эйлеров цикл,
необходимо и достаточно, чтобы в
каждом узле графа число входящих
и выходящих дуг было одинаковым
[ САМ. доказать данную теорему]
в электронном курсе: раздел 3/Материалы для
самостоятельного изучения]
Замечание: задачу о Кенигсбергских мостах
a – имеет эйлеров цикл
b – не имеет эйлерова цикла
Пример:
решить невозможно, так как все вершины
графа задачи имеют нечетные степени
e
Пример:
d
b
b
c
a
c
a
c
a – эйлеров граф
b – не эйлеров граф
a
d
d
a
e
d
f
b
a
e
c
a
b
b
b

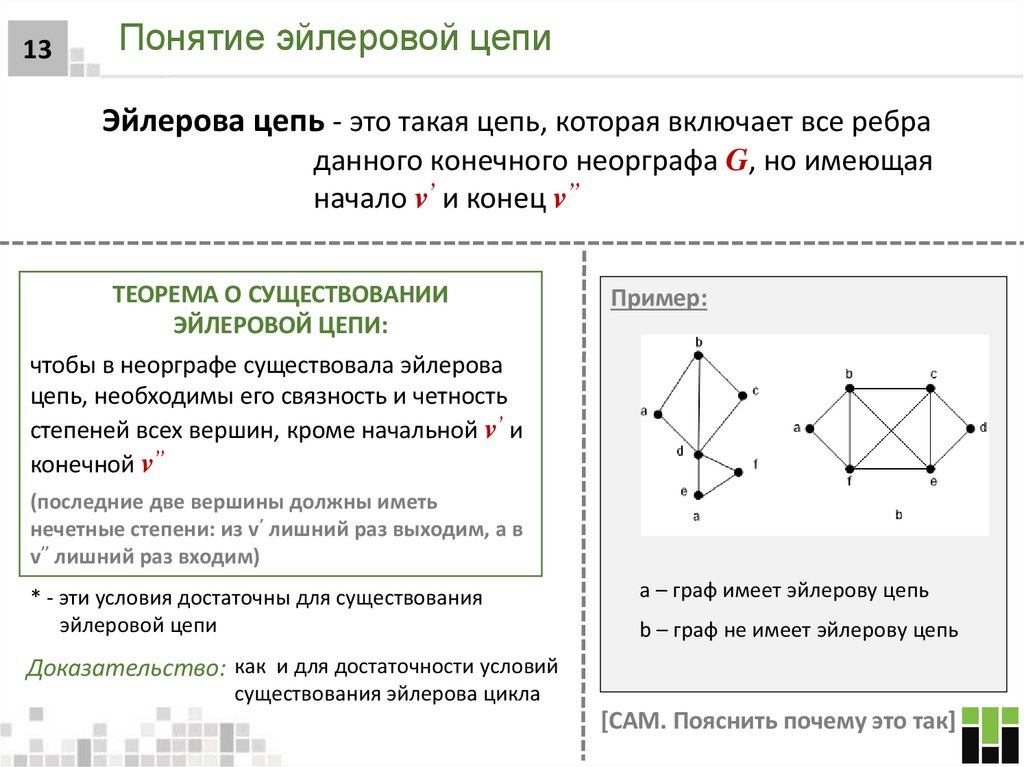
13. Понятие эйлеровой цепи

13
Понятие эйлеровой цепи
Эйлерова цепь - это такая цепь, которая включает все ребра
данного конечного неорграфа G, но имеющая
начало v’ и конец v’’
ТЕОРЕМА О СУЩЕСТВОВАНИИ
ЭЙЛЕРОВОЙ ЦЕПИ:
Пример:
чтобы в неорграфе существовала эйлерова
цепь, необходимы его связность и четность
степеней всех вершин, кроме начальной v’ и
конечной v’’
(последние две вершины должны иметь
нечетные степени: из v ’ лишний раз выходим, а в
v ’’ лишний раз входим)
* - эти условия достаточны для существования
эйлеровой цепи
a – граф имеет эйлерову цепь
b – граф не имеет эйлерову цепь
Доказательство: как и для достаточности условий
существования эйлерова цикла
[САМ. Пояснить почему это так]

14. Алгоритмы поиска эйлерова цикла

14
Алгоритмы поиска эйлерова цикла
Алгоритм на основе поиска циклов
(описание на псевдокоде)
Вход: эйлеров граф G(V,E), заданный матрицей
смежности
Пусть:
Выход: последовательность вершин эйлерова
цикла
C – стек для хранения вершин
эйлерова цикла
S – стек для хранения вершин
1. Выбрать произвольно вершину а
9. end if
2. a >> S (поместить вершину a в стек S)
10. end while
3. while S ≠ 0 (стек S не пуст) do
4. x = top(S) (верхний элемент стека S)
5. if имеется непройденное ребро (x, y)
6. then пометить ребро (x, y) как пройденное
7. y >> S (поместить вершину y в стек S)
8. else
- переместить вершину x из стека S в стек С
- удалить вершину x из стека S
временная сложность
алгоритма - O(m) (m – число
ребер)
данный алгоритм может быть
реализован рекурсивно

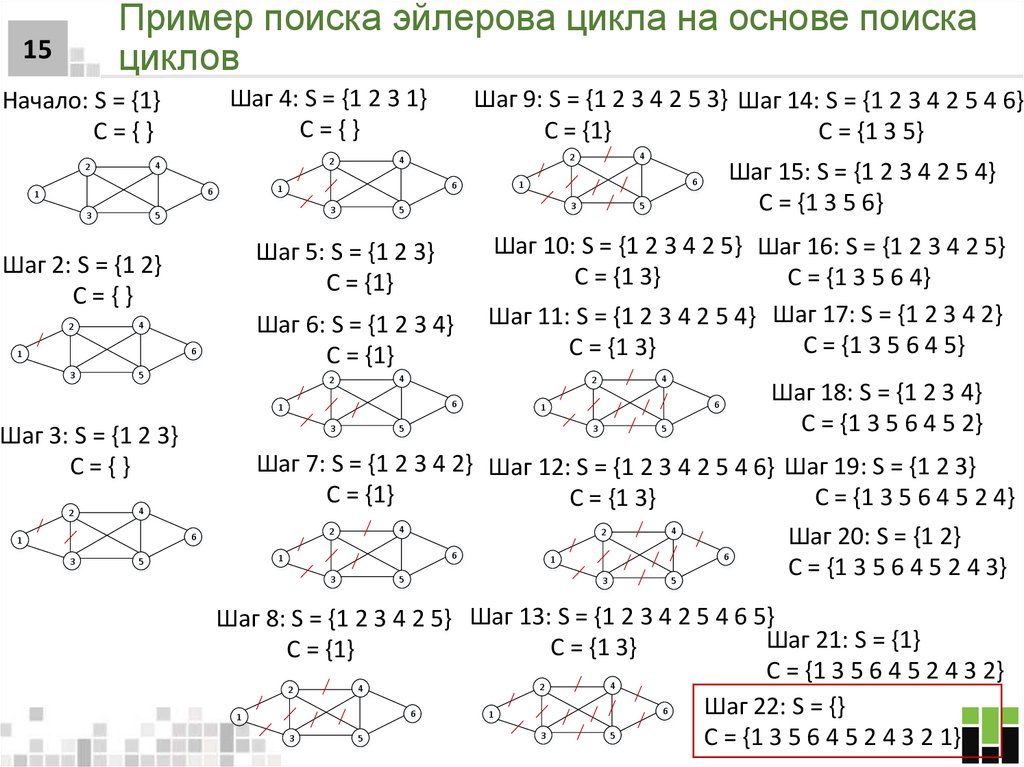
15. Пример поиска эйлерова цикла на основе поиска циклов

15
Шаг 4: S = {1 2 3 1}
C={}
Начало: S = {1}
C={}
3
3
5
Шаг 2: S = {1 2}
C={}
2
Шаг 6: S = {1 2 3 4}
C = {1}
4
6
1
3
3
5
Шаг 5: S = {1 2 3}
C = {1}
5
6
3
2
5
3
4
2
6
3
Шаг 18: S = {1 2 3 4}
C = {1 3 5 6 4 5 2}
6
1
5
Шаг 7: S = {1 2 3 4 2} Шаг 12: S = {1 2 3 4 2 5 4 6} Шаг 19: S = {1 2 3}
C = {1}
C = {1 3 5 6 4 5 2 4}
C = {1 3}
4
1
4
2
1
Шаг 3: S = {1 2 3}
C={}
5
Шаг 10: S = {1 2 3 4 2 5} Шаг 16: S = {1 2 3 4 2 5}
C = {1 3}
C = {1 3 5 6 4}
Шаг 11: S = {1 2 3 4 2 5 4} Шаг 17: S = {1 2 3 4 2}
C = {1 3 5 6 4 5}
C = {1 3}
4
2
Шаг 15: S = {1 2 3 4 2 5 4}
C = {1 3 5 6}
6
1
6
1
6
1
4
2
4
2
4
2
Шаг 9: S = {1 2 3 4 2 5 3} Шаг 14: S = {1 2 3 4 2 5 4 6}
C = {1}
C = {1 3 5}
6
1
5
3
4
2
6
1
5
3
5
Шаг 20: S = {1 2}
C = {1 3 5 6 4 5 2 4 3}
Шаг 8: S = {1 2 3 4 2 5} Шаг 13: S = {1 2 3 4 2 5 4 6 5}
Шаг 21: S = {1}
C = {1 3}
C = {1}
C = {1 3 5 6 4 5 2 4 3 2}
Шаг 22: S = {}
C = {1 3 5 6 4 5 2 4 3 2 1}
2
2
4
6
1
3
5
4
6
1
3
5

16. Алгоритмы поиска эйлерова цикла

16
Алгоритмы поиска эйлерова цикла
Алгоритм Флёри
Вход: эйлеров граф G(V,E), заданный матрицей смежности
Выход: последовательность вершин эйлерова цикла
Нумеруем ребра по следующим правилам:
Первое правило:
• начиная с произвольной вершины u присваиваем
произвольному ребру {u, v}, инцидентному u, номер 1
• удаляем из графа ребро {u, v}, переходим в вершину v
Второе правило:
• пусть w – вершина, в которую мы пришли в результате
выполнения предыдущего шага, и k – номер, присвоенный
некоторому ребру на этом шаге
временная сложность алгоритма
- O(m2) (m – число ребер )
• выбираем любое ребро {w, t}, инцидентное вершине w, причем
мост выбирается только в том случае, когда нет других
возможностей
• присваиваем ребру номер k + 1, удаляем его из графа (вместе с
образующимися изолированными вершинами) и переходим в
вершину t
Этот процесс заканчивается, когда все ребра графа удалены

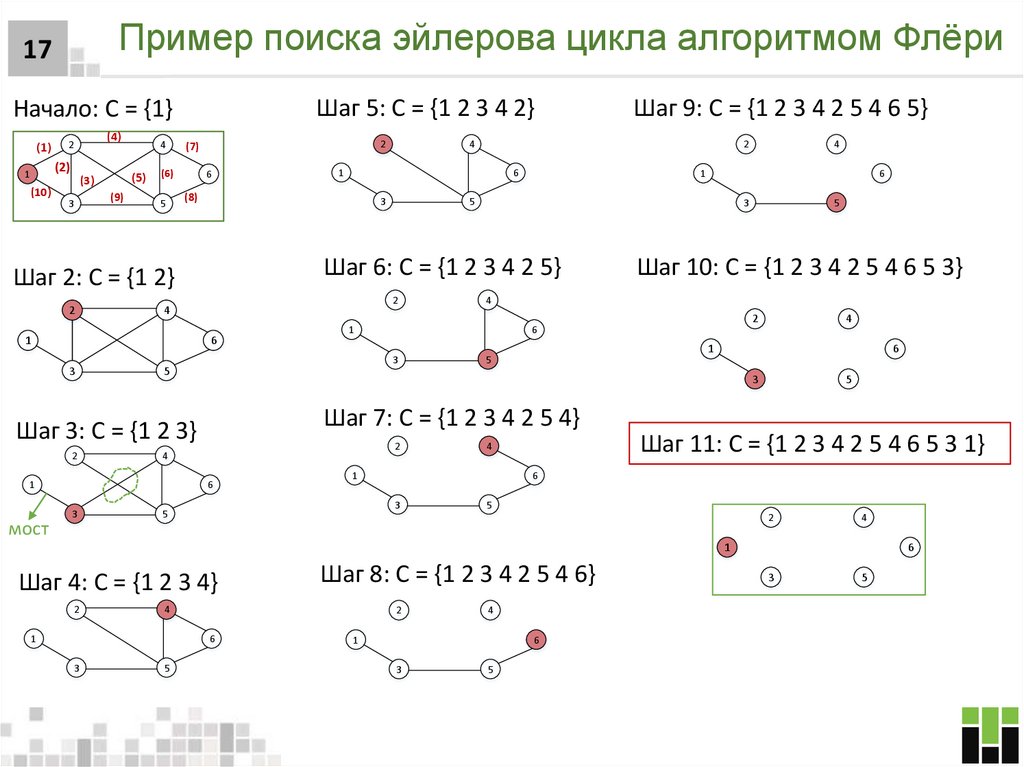
17. Пример поиска эйлерова цикла алгоритмом Флёри

17
Шаг 5: С = {1 2 3 4 2}
Начало: С = {1}
(1)
(4)
2
(2)
1
(10)
(5)
(3)
3
4
(9)
(6)
5
2
(7)
6
6
мост
2
4
1
5
6
5
Шаг 7: С = {1 2 3 4 2 5 4}
2
6
3
4
3
4
1
5
Шаг 10: С = {1 2 3 4 2 5 4 6 5 3}
6
3
Шаг 3: С = {1 2 3}
2
3
1
5
6
5
2
4
1
Шаг 6: С = {1 2 3 4 2 5}
4
1
3
6
3
Шаг 2: С = {1 2}
2
2
4
1
(8)
Шаг 9: С = {1 2 3 4 2 5 4 6 5}
1
6
3
5
Шаг 11: С = {1 2 3 4 2 5 4 6 5 3 1}
4
5
2
4
1
Шаг 4: С = {1 2 3 4}
2
4
1
2
6
3
Шаг 8: С = {1 2 3 4 2 5 4 6}
5
4
1
6
3
5
6
3
5

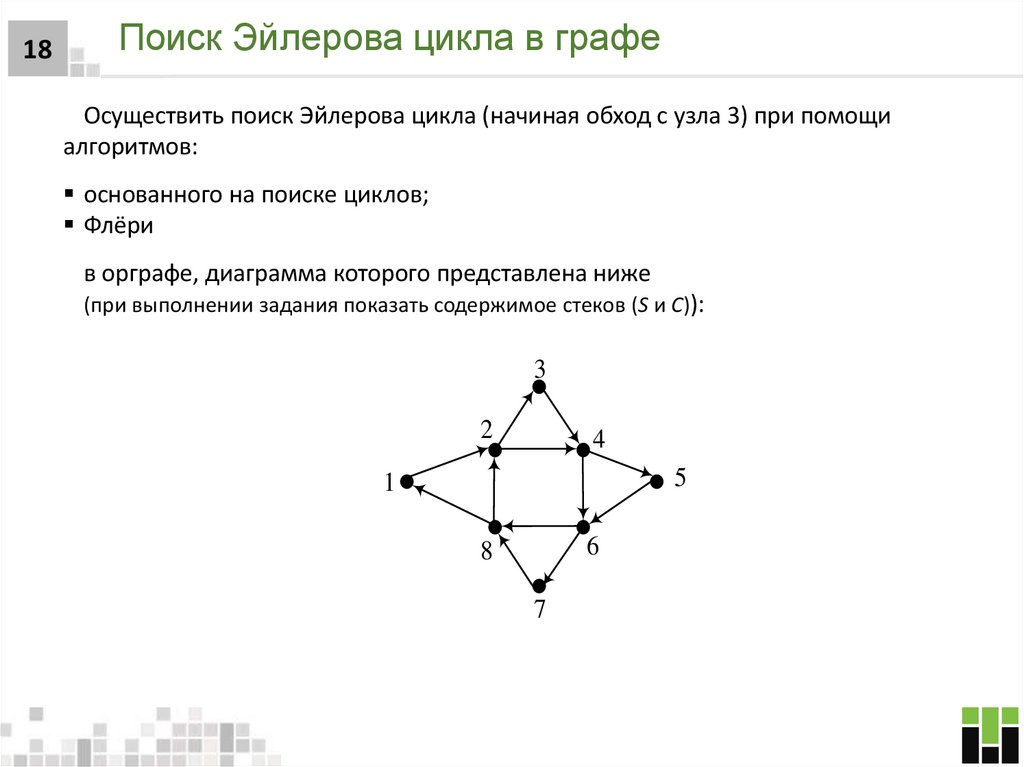
18. Поиск Эйлерова цикла в графе

18
Поиск Эйлерова цикла в графе
Осуществить поиск Эйлерова цикла (начиная обход с узла 3) при помощи
алгоритмов:
основанного на поиске циклов;
Флёри
в орграфе, диаграмма которого представлена ниже
(при выполнении задания показать содержимое стеков (S и C)):
3
2
4
5
1
6
8
7

19. Экстремальные пути во взвешенных орграфах

19
Экстремальные пути во взвешенных орграфах
Орграф называется взвешенным (нагруженным), если дугам этого
графа поставлены в соответствие некоторые числа, называемые
весами или длинами, или стоимостями
При этом:
веса, приписанные дугам могут быть
положительными, отрицательными или
нулевыми
вес (или длинна, или стоимость) пути,
состоящего из некоторой
последовательности дуг – это число,
равное сумме длин дуг, входящих в этот
путь
для не нагруженного графа кратчайший
путь - это путь с минимальным общим
числом дуг (каждая дуга считается столько
Такой граф может быть задан
матрицей весов C cij
n n
(n – число узлов графа):
0, если узлы vi = v j ,
сij , если узлы vi и v j не соеденины,
d , если (vi ,v j ) - дуга веса d
Пример:
0 1 2 4
0 5
С 0 3
0
6 0
раз, сколько она содержится в этом пути)
Длина пути (x1, x2, x5, x4) равна 1 + 5 + 6 = 12

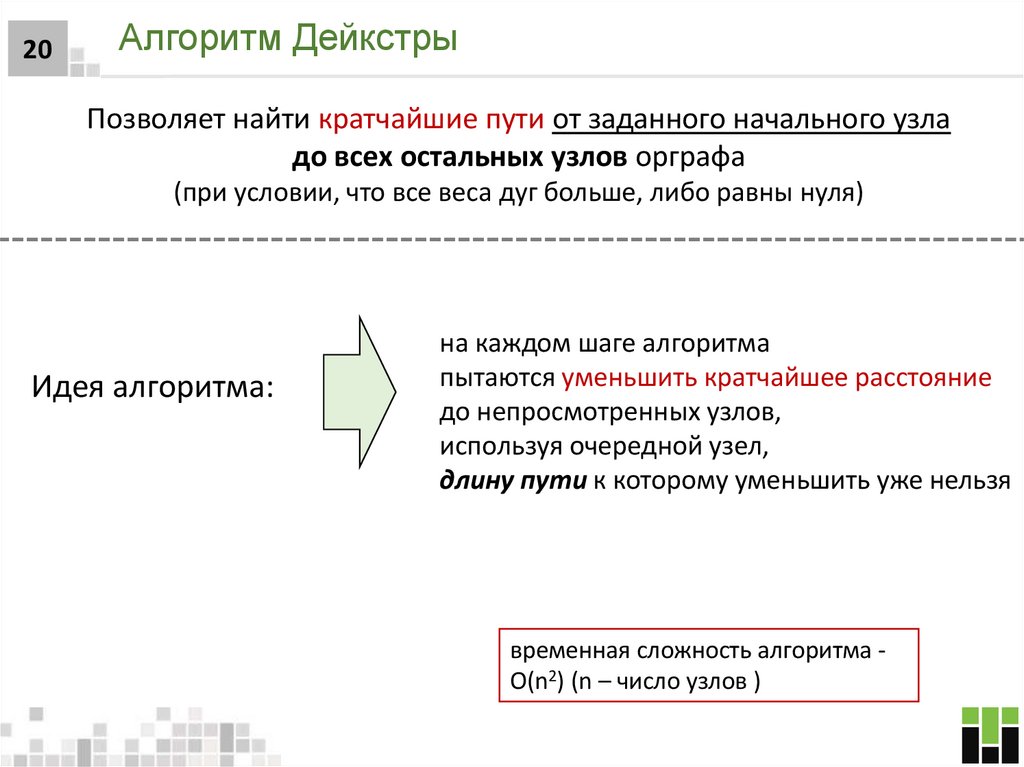
20. Алгоритм Дейкстры

20
Алгоритм Дейкстры
Позволяет найти кратчайшие пути от заданного начального узла
до всех остальных узлов орграфа
(при условии, что все веса дуг больше, либо равны нуля)
Идея алгоритма:
на каждом шаге алгоритма
пытаются уменьшить кратчайшее расстояние
до непросмотренных узлов,
используя очередной узел,
длину пути к которому уменьшить уже нельзя
временная сложность алгоритма O(n2) (n – число узлов )

21. Алгоритм Дейкстры

21
Алгоритм Дейкстры
В частности:
в течение работы алгоритма каждому узлу v орграфа присваивается число d[v],
равное расстоянию от заданного узла a до v
перед началом работы d[v] совпадает с весом дуги (а, v), если такая
существует, или равно бесконечности в противном случае
далее необходимо обходить узлы орграфа и уточнять значения d[v]
на каждом шаге алгоритма отмечается один узел u, до которого уже найден
кратчайший путь от a и расстояние d[u] до него
далее полученное значение d[u], отмеченного узла не меняется
для оставшихся, неотмеченных узлов v, число d[v] будет меняется с учетом
того, что искомый кратчайший путь до них от a будет проходить через
последний отмеченный узел u
алгоритм завершится в тот момент, когда все возможные узлы будут отмечены
и получат свои окончательные значения d[v]
[ САМ. Ознакомится с примером поиска кратчайших путей при
помощи алгоритма Дейкстры и выполнить самостоятельное
задание (в электронном курсе: раздел 3/Материалы для самостоятельного
изучения/Алгоритм Дейкстры_пример]

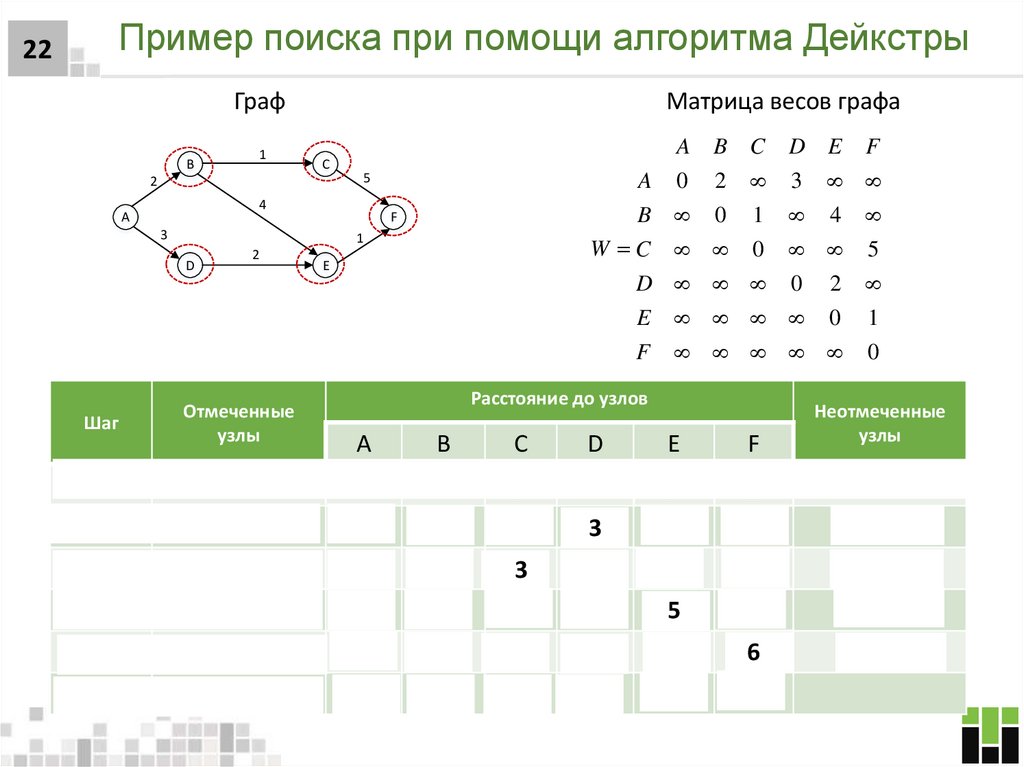
22. Пример поиска при помощи алгоритма Дейкстры

22
Граф
1
B
Матрица весов графа
A
A 0
B
W C
D
E
F
C
5
2
4
A
F
3
1
2
D
Шаг
Отмеченные
узлы
0
E
B
2
0
C
1
0
Расстояние до узлов
C
D
E
F
D
3
0
E
4
2
0
F
5
1
0
Неотмеченные
узлы
A
B
A
0
2
1
B
0
2
3
3
6
C, D, E, F
2
D
0
2
3
3
5
C, E, F
3
C
0
2
3
м
3
5
м
м
E,мF
4
E
0
2
3
3
5
6
Fм
5
F
0
2
3
3
5
6
3
B, C, D, E, F

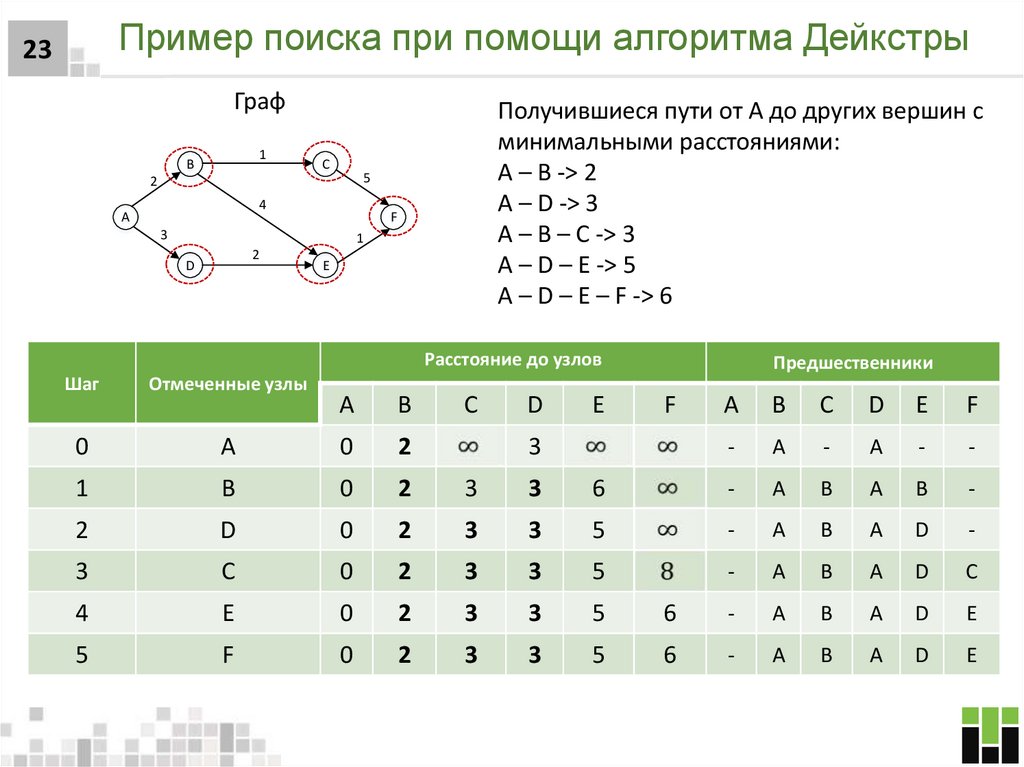
23. Пример поиска при помощи алгоритма Дейкстры

23
Граф
1
B
Получившиеся пути от А до других вершин с
минимальными расстояниями:
A – B -> 2
A – D -> 3
А – В – С -> 3
A – D – E -> 5
A – D – E – F -> 6
C
5
2
4
A
F
3
1
2
D
E
Расстояние до узлов
Шаг
Отмеченные узлы
0
A
B
C
D
A
0
2
1
B
0
2
3
3
2
D
0
2
3
3
C
0
2
4
E
0
5
F
0
E
Предшественники
F
A
B
C
D
E
F
-
A
-
A
-
-
6
-
A
B
A
B
-
3
5
-
A
B
A
D
-
3
3
5
-
A
B
A
D
C
2
3
3
5
6
-
A
B
A
D
E
2
3
3
5
6
-
A
B
A
D
E
3

24. Общая задача поиска кратчайших путей

24
Общая задача поиска кратчайших путей
Общая задача нахождения кратчайших путей –
это нахождение для каждой пары узлов (v, u) орграфа
такого пути от узла v в u, что его длина будет минимальна
среди всех возможных путей от v к u
данную задачу можно решить, последовательно применяя
алгоритм Дейкстры для каждого узла, объявляемого в
качестве начального
существует прямые способы решения, например алгоритмы
Флойда, Форда- Беллмана и др.

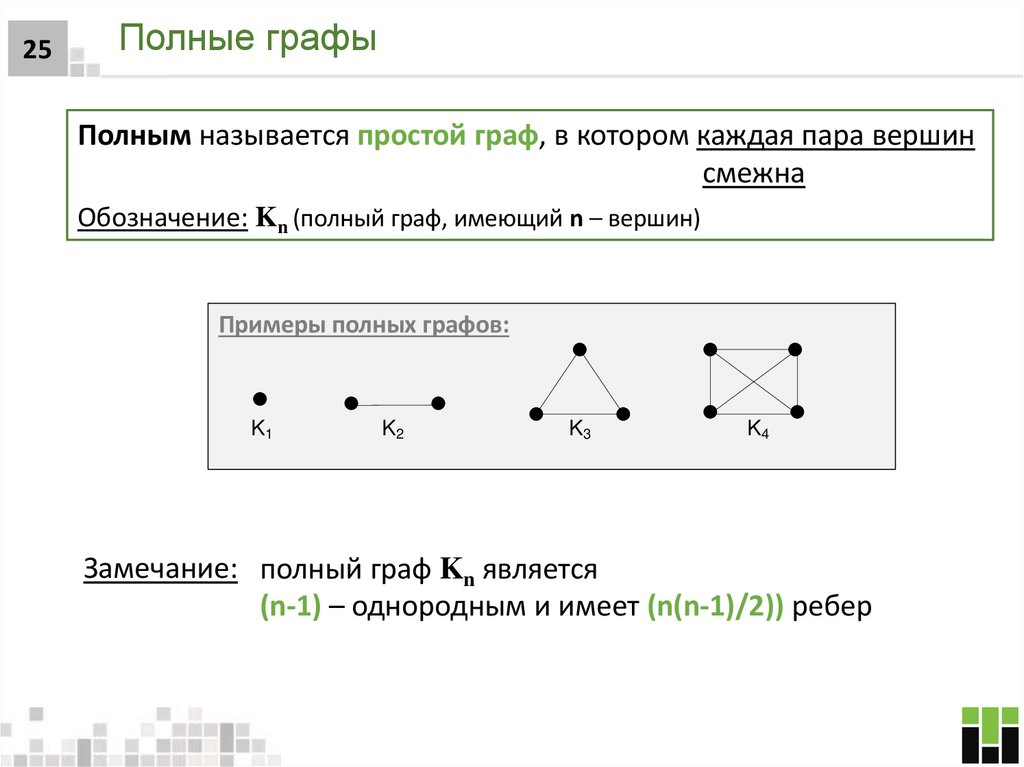
25. Полные графы

25
Полные графы
Полным называется простой граф, в котором каждая пара вершин
смежна
Обозначение: Kn (полный граф, имеющий n – вершин)
Примеры полных графов:
K1
K2
K3
K4
Замечание: полный граф Kn является
(n-1) – однородным и имеет (n(n-1)/2)) ребер

26. Двудольные графы

26
Двудольным называется граф G = (V, E), множество вершин V которого
можно разбить на два таких непересекающихся подмножества V1 и V2,
что каждое ребро, принадлежащее множеству Е ребер графа, имеет одну
концевую вершину в подмножестве V1, а другую – в подмножестве V2
Пара таких множеств (V1, V2) - называется двудольным разбиением
множества V вершин графа G
Если в простом двудольном
графе G = (V, E) с разбиением
(V1, V2) для каждой пары вершин
vi , v j V1 V2 существует ребро
Примеры двудольных графов:
v , v E , то граф G называется
i
K1,1
K1, 2
K2,2
K2,3
j
полным двудольным графом
Обозначение: K n ,m
где m V1 , n V2

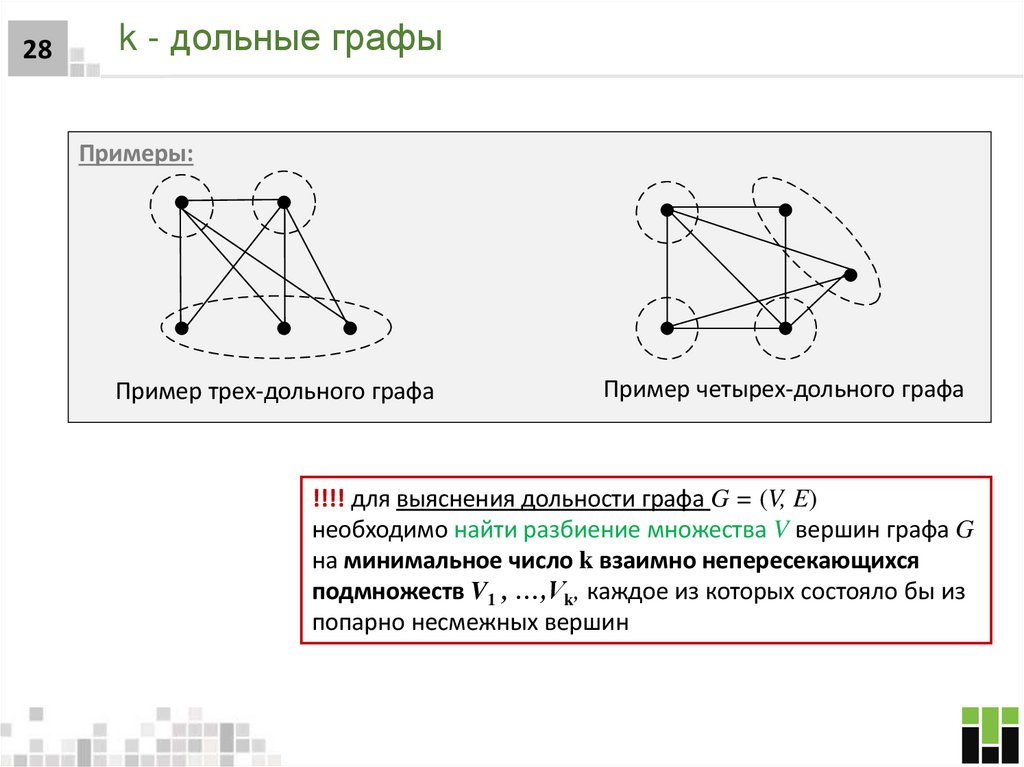
27. k - дольные графы

27
k - дольные графы
K – дольным называется граф G = (V, E), множество вершин V которого
можно разбить на k попарно непересекающихся подмножества V1 ,
…,Vk таких, что каждое ребро, принадлежащее множеству Е ребер
графа G, имеет одну концевую вершину в одном из этих
подмножеств, а другую – в другом
Простой k-дольный граф G = (V, E), множество V вершин которого
можно разбить на k попарно непересекающихся подмножеств V1 , …,Vk
множества вершин V граф G, называется полным k- дольным
графом, если выполняются условия:
каждое подмножество разбиения должно состоять из
несмежных друг другу вершин
при этом каждая из вершин каждого подмножества должна
быть смежна каждой другой вершине в каждом другом
подмножестве

28. k - дольные графы

28
k - дольные графы
Примеры:
Пример трех-дольного графа
Пример четырех-дольного графа
!!!! для выяснения дольности графа G = (V, E)
необходимо найти разбиение множества V вершин графа G
на минимальное число k взаимно непересекающихся
подмножеств V1 , …,Vk, каждое из которых состояло бы из
попарно несмежных вершин

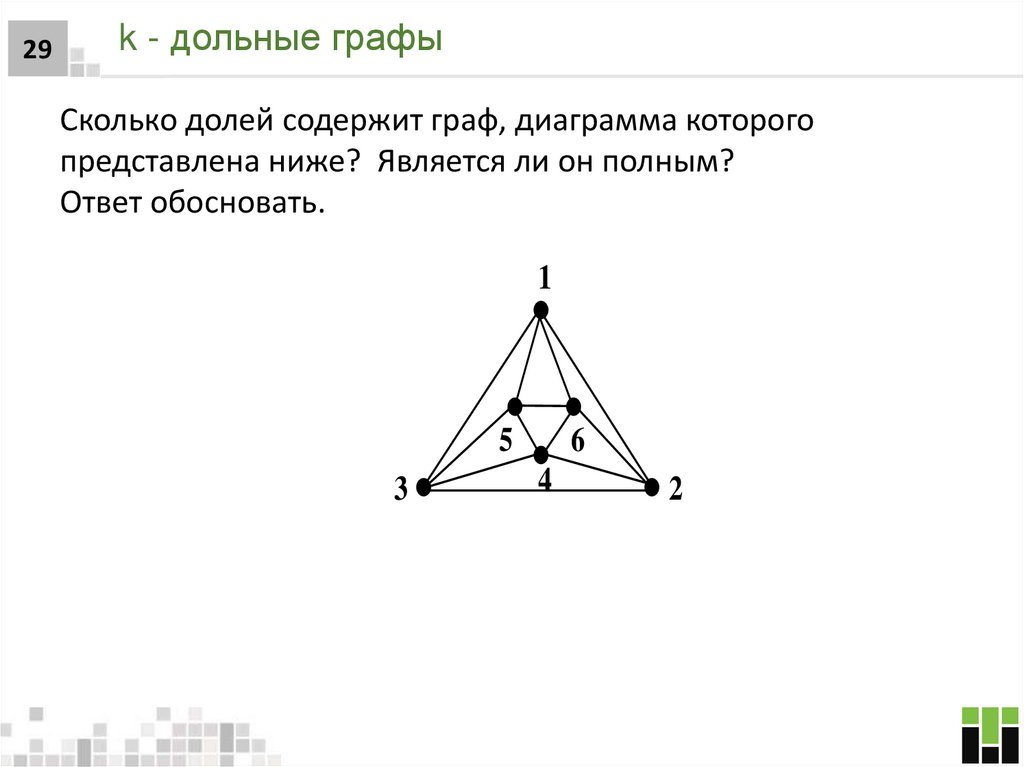
29. k - дольные графы

29
k - дольные графы
Сколько долей содержит граф, диаграмма которого
представлена ниже? Является ли он полным?
Ответ обосновать.
1
5
3
6
4
2

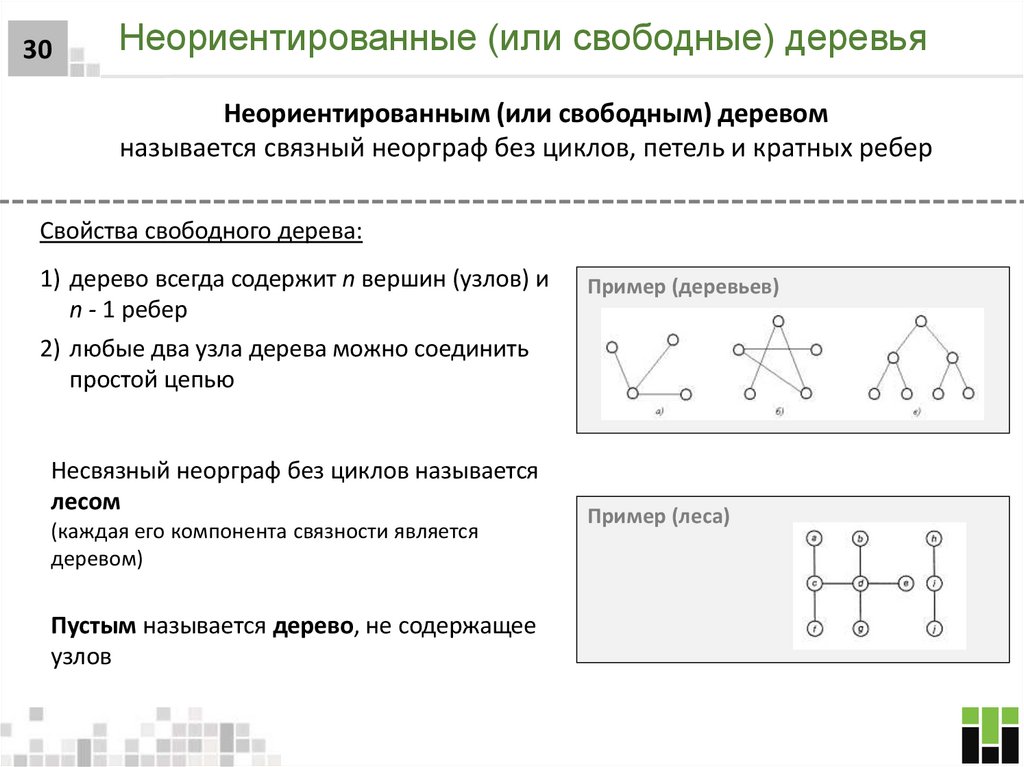
30. Неориентированные (или свободные) деревья

30
Неориентированные (или свободные) деревья
Неориентированным (или свободным) деревом
называется связный неорграф без циклов, петель и кратных ребер
Свойства свободного дерева:
1) дерево всегда содержит n вершин (узлов) и
n - 1 ребер
Пример (деревьев)
2) любые два узла дерева можно соединить
простой цепью
Несвязный неорграф без циклов называется
лесом
(каждая его компонента связности является
деревом)
Пустым называется дерево, не содержащее
узлов
Пример (леса)

31. Неориентированные (или свободные) деревья

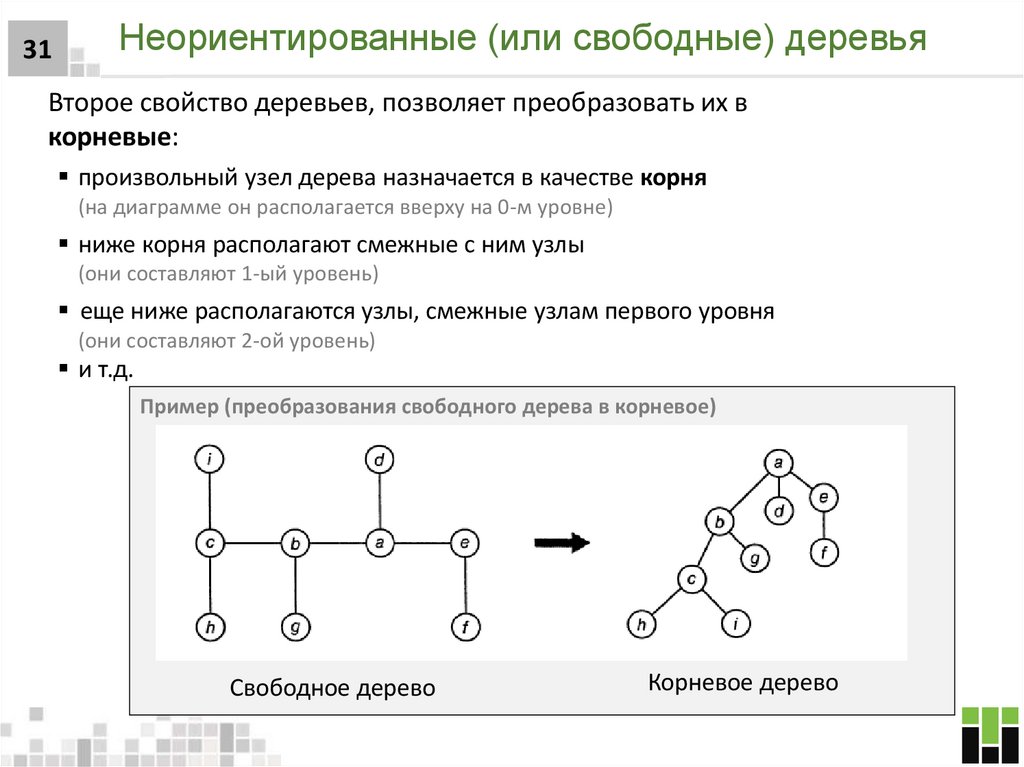
31
Неориентированные (или свободные) деревья
Второе свойство деревьев, позволяет преобразовать их в
корневые:
произвольный узел дерева назначается в качестве корня
(на диаграмме он располагается вверху на 0-м уровне)
ниже корня располагают смежные с ним узлы
(они составляют 1-ый уровень)
еще ниже располагаются узлы, смежные узлам первого уровня
(они составляют 2-ой уровень)
и т.д.
Пример (преобразования свободного дерева в корневое)
Свободное дерево
Корневое дерево

32. Ориентированные (корневые) деревья

32
Ориентированные (корневые) деревья
Ориентированным (корневым) деревом
называется бесконтурный орграф, у которого полустепень захода любого
узла не больше 1 и существует ровно один узел, называемый корнем,
полустепень захода которого равна 0
(в ориентированном дереве любой узел достижим из корня)
Типы узлов корневых деревьев:
потомки и предки:
узел v в корневом дереве называют потомком узла u, если
существует простой маршрут из u в v (ненулевой длины) в
этом же случае узел u называют предком узла v
родитель (отец) и ребенок (сын):
если длина маршрута из u в v равна 1, то узел v называют
ребенком (непосредственным потомком) узла u, который
при этом именуется родителем узла v

33. Ориентированные (корневые) деревья

33
Ориентированные (корневые) деревья
Узлы, имеющие общего родителя,
называют родственниками
Узел, не имеющий потомков, называют,
листом (или терминальным узлом), в
противном случае – внутренним узлом
Узел v вместе со всеми своими
потомками называется поддеревом с
корнем в узле v
Орграф называется
ориентированным лесом, если
каждая его
слабая компонента связности
является ориентированным деревом
Ориентированное дерево, у
которого каждый узел, отличный от
корня, есть лист, называют кустом

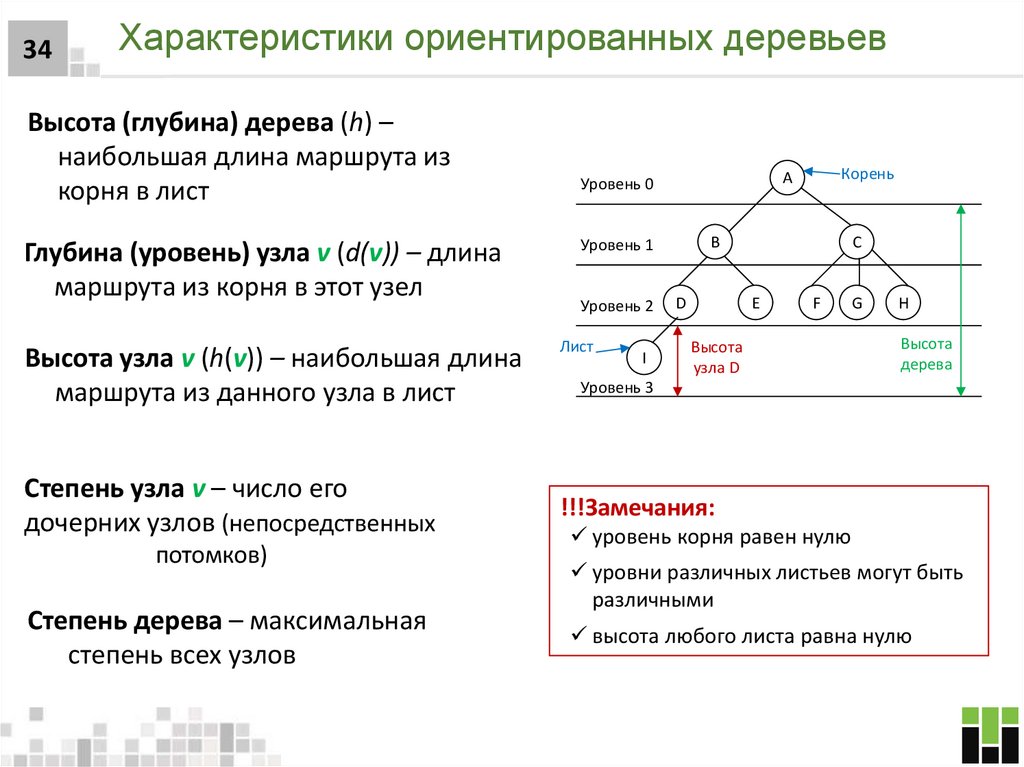
34. Характеристики ориентированных деревьев

34
Характеристики ориентированных деревьев
Высота (глубина) дерева (h) –
наибольшая длина маршрута из
корня в лист
Глубина (уровень) узла v (d(v)) – длина
маршрута из корня в этот узел
Высота узла v (h(v)) – наибольшая длина
маршрута из данного узла в лист
Степень узла v – число его
дочерних узлов (непосредственных
потомков)
Степень дерева – максимальная
степень всех узлов
B
Уровень 1
Уровень 2
Лист
I
Корень
A
Уровень 0
D
C
E
F
Высота
узла D
G
H
Высота
дерева
Уровень 3
!!!Замечания:
уровень корня равен нулю
уровни различных листьев могут быть
различными
высота любого листа равна нулю

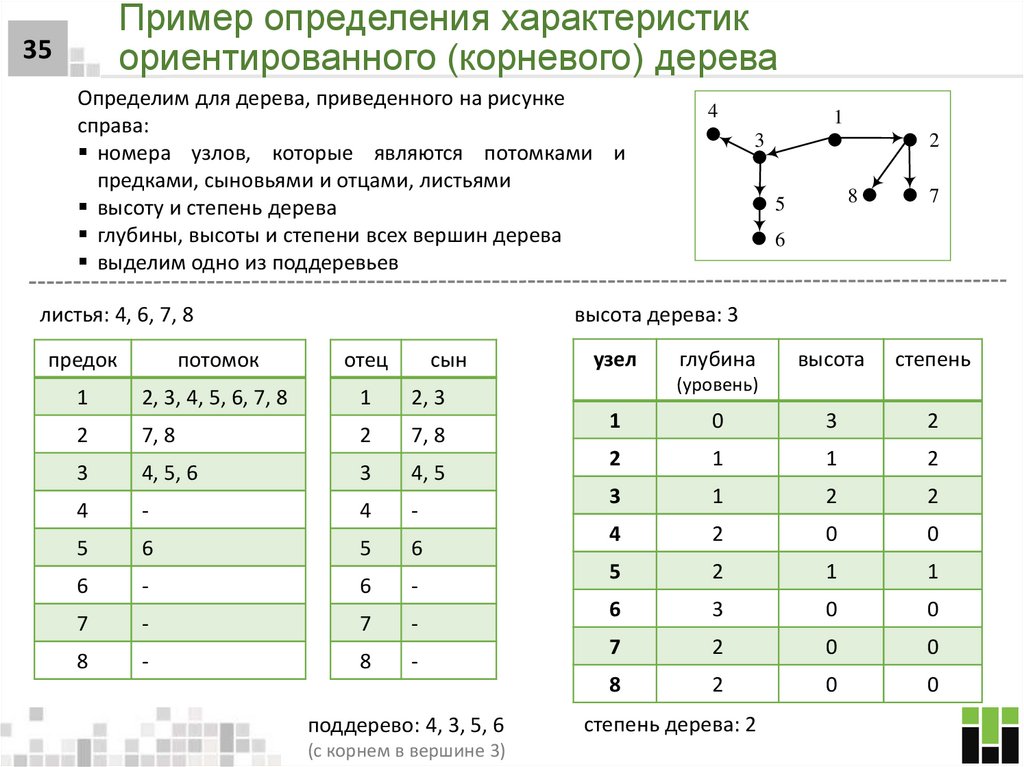
35. Пример определения характеристик ориентированного (корневого) дерева

35
Определим для дерева, приведенного на рисунке
справа:
номера узлов, которые являются потомками и
предками, сыновьями и отцами, листьями
высоту и степень дерева
глубины, высоты и степени всех вершин дерева
выделим одно из поддеревьев
листья: 4, 6, 7, 8
4
1
3
2
8
5
7
6
высота дерева: 3
предок
потомок
отец
сын
1
2, 3, 4, 5, 6, 7, 8
1
2, 3
2
7, 8
2
7, 8
3
4, 5, 6
3
4, 5
4
-
4
-
5
6
5
6
6
-
6
-
7
-
7
-
8
-
8
-
поддерево: 4, 3, 5, 6
(с корнем в вершине 3)
узел
глубина
высота
степень
(уровень)
1
0
3
2
2
1
1
2
3
1
2
2
4
2
0
0
5
2
1
1
6
3
0
0
7
2
0
0
8
2
0
0
степень дерева: 2

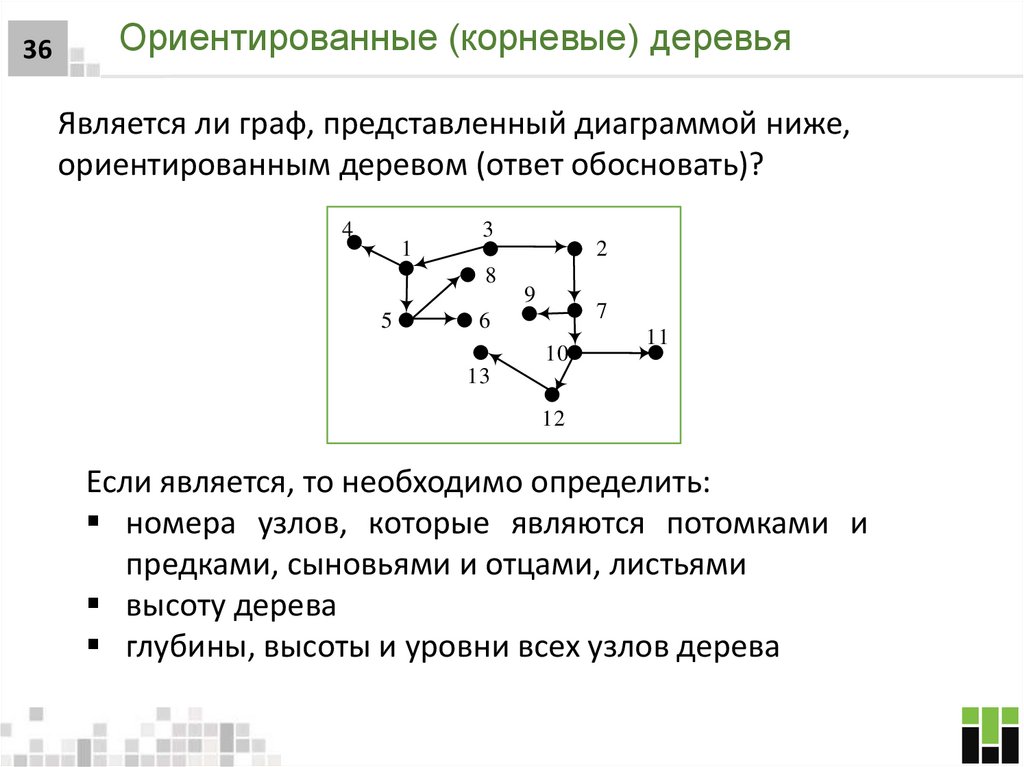
36. Ориентированные (корневые) деревья

36
Ориентированные (корневые) деревья
Является ли граф, представленный диаграммой ниже,
ориентированным деревом (ответ обосновать)?
4
1
3
8
5
2
9
7
6
10
11
13
12
Если является, то необходимо определить:
номера узлов, которые являются потомками и
предками, сыновьями и отцами, листьями
высоту дерева
глубины, высоты и уровни всех узлов дерева

37. Задача о поиске минимального остовного дерева

37
Задача о поиске минимального остовного дерева
Остовным деревом связного неорграфа (орграфа) G называется
любой его подграф, содержащий все вершины (узлы) неорграфа
(графа) G и являющийся деревом
Суть задачи:
пусть G - связный взвешенный граф, тогда задача построения
минимального остовного дерева заключается в том, чтобы из
множества остовных деревьев графа G найти дерево, у которого
сумма длин ребер минимальна
Рассмотрим алгоритмы поиска:
Прима
Кра (у)скала

38. Задача о поиске минимального остовного дерева

38
Задача о поиске минимального остовного дерева
Алгоритм Прима:
Шаг 1 (установка начальных значений):
вводится матрица весов графа G (C)
Шаг 2:
выбирается в графе G ребро минимальной длины
строится граф G2, состоящий из данного ребра и инцидентных ему вершин
полагается i = 2
Шаг 3:
если i = n, где n - число вершин графа, то поиск заканчивается (задача решена)
в противном случае перейти к шагу 4
Шаг 4:
строится граф Gi +1, добавлением к графу Gi нового ребра минимальной длины,
выбранного среди ребер графа G, каждое из которых инцидентно какой-нибудь
вершине графа Gi и одновременно инцидентно какой-нибудь вершине графа G, не
содержащейся в Gi
вместе с этим ребром включается в Gi +1 и инцидентная ему вершина, не
содержащаяся в Gi.
полагается i:= i +1 и осуществляется переход к шагу 3

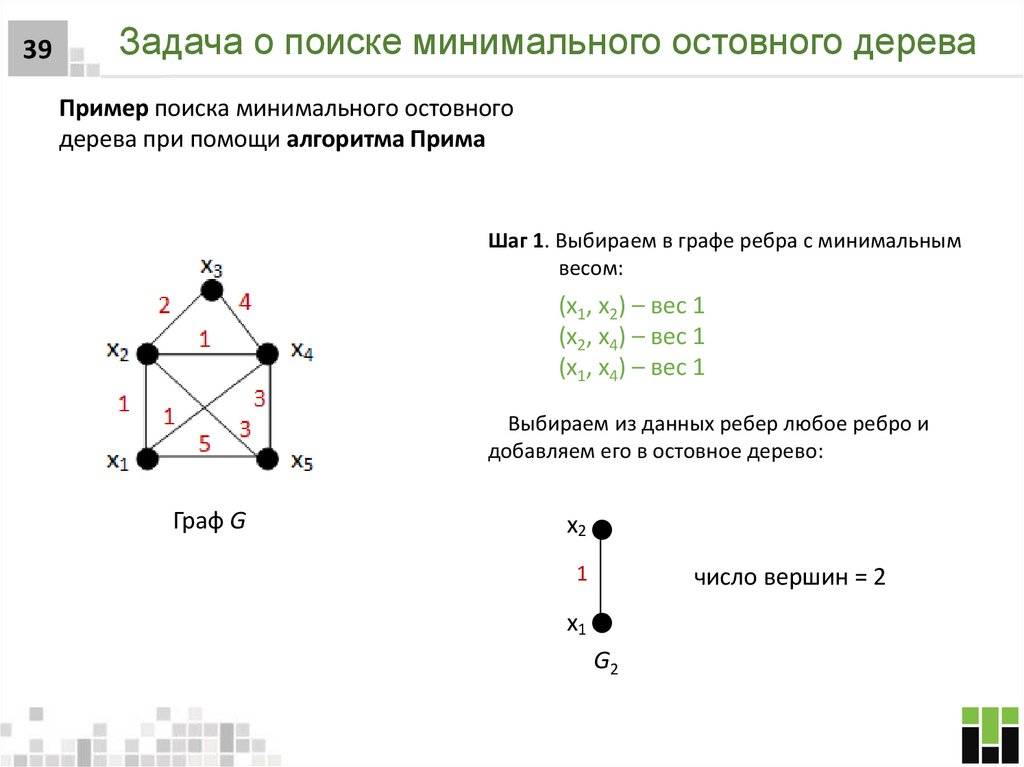
39. Задача о поиске минимального остовного дерева

39
Задача о поиске минимального остовного дерева
Пример поиска минимального остовного
дерева при помощи алгоритма Прима
Шаг 1. Выбираем в графе ребра с минимальным
весом:
(x1, x2) – вес 1
(x2, x4) – вес 1
(x1, x4) – вес 1
Выбираем из данных ребер любое ребро и
добавляем его в остовное дерево:
Граф G
x2
1
число вершин = 2
x1
G2

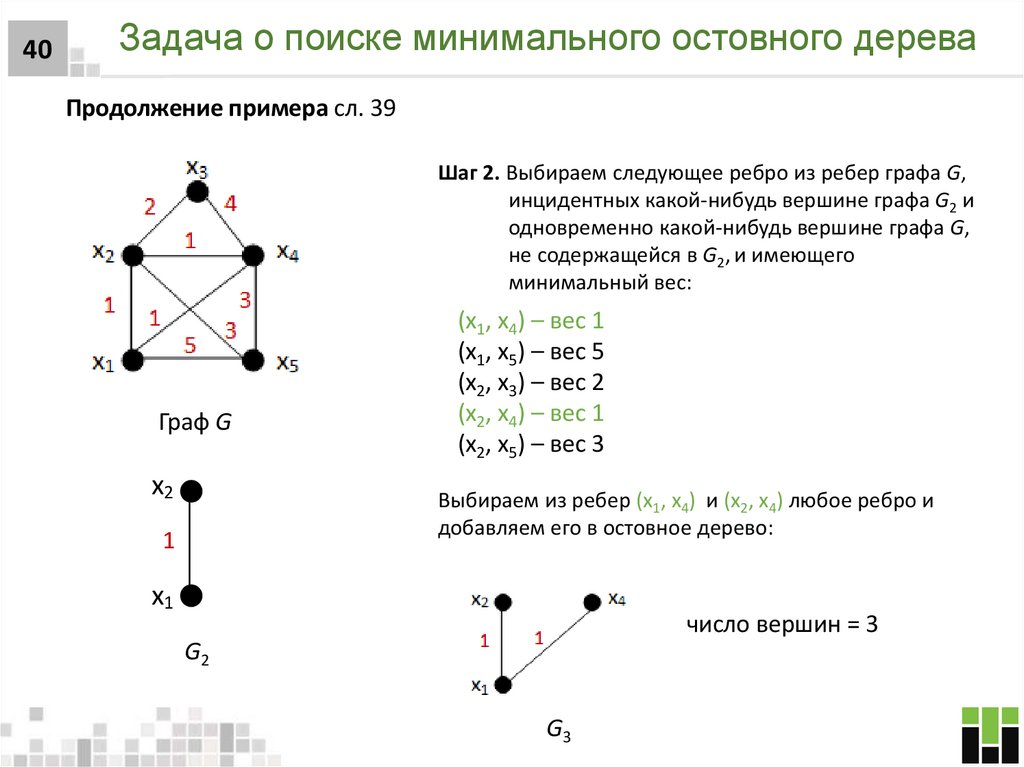
40. Задача о поиске минимального остовного дерева

40
Задача о поиске минимального остовного дерева
Продолжение примера сл. 39
Шаг 2. Выбираем следующее ребро из ребер графа G,
инцидентных какой-нибудь вершине графа G2 и
одновременно какой-нибудь вершине графа G,
не содержащейся в G2, и имеющего
минимальный вес:
Граф G
x2
(x1, x4) – вес 1
(x1, x5) – вес 5
(x2, x3) – вес 2
(x2, x4) – вес 1
(x2, x5) – вес 3
Выбираем из ребер (x1, x4) и (x2, x4) любое ребро и
добавляем его в остовное дерево:
1
x1
число вершин = 3
G2
G3

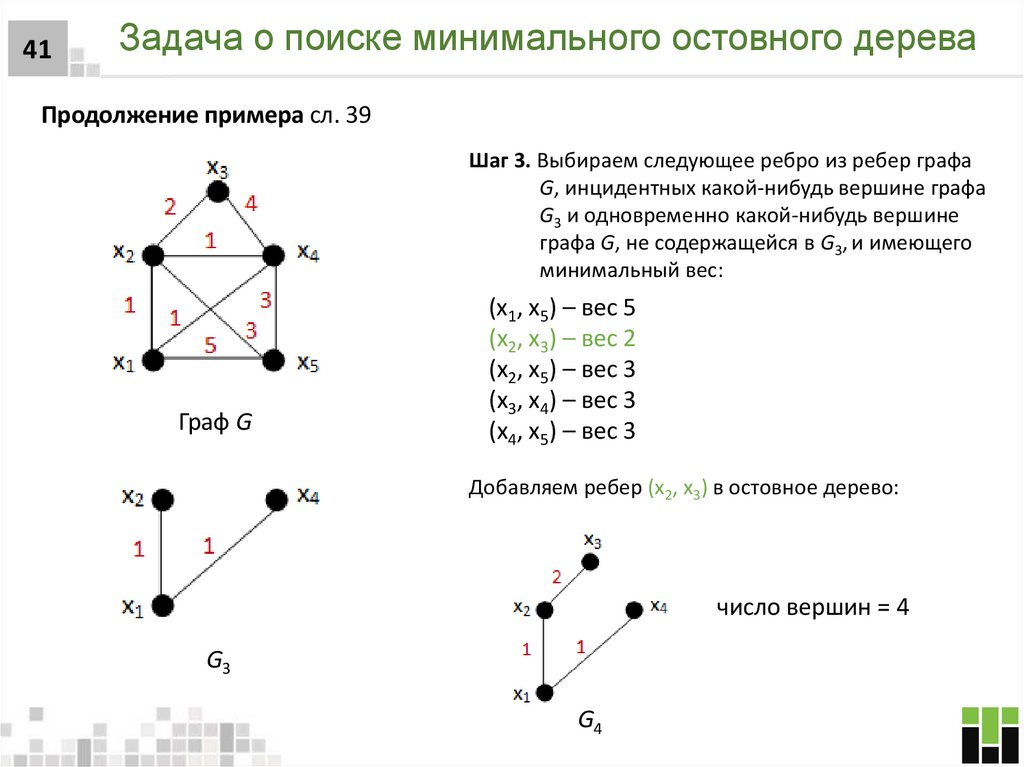
41. Задача о поиске минимального остовного дерева

41
Задача о поиске минимального остовного дерева
Продолжение примера сл. 39
Шаг 3. Выбираем следующее ребро из ребер графа
G, инцидентных какой-нибудь вершине графа
G3 и одновременно какой-нибудь вершине
графа G, не содержащейся в G3, и имеющего
минимальный вес:
Граф G
(x1, x5) – вес 5
(x2, x3) – вес 2
(x2, x5) – вес 3
(x3, x4) – вес 3
(x4, x5) – вес 3
Добавляем ребер (x2, x3) в остовное дерево:
число вершин = 4
G3
G4

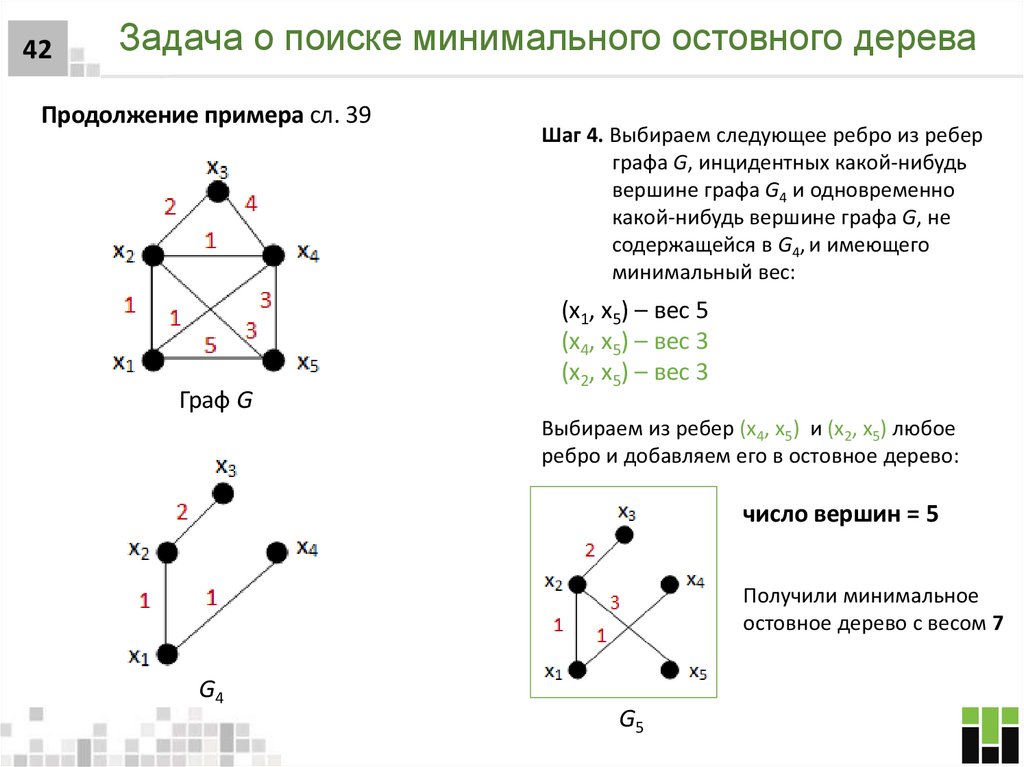
42. Задача о поиске минимального остовного дерева

42
Задача о поиске минимального остовного дерева
Продолжение примера сл. 39
Граф G
Шаг 4. Выбираем следующее ребро из ребер
графа G, инцидентных какой-нибудь
вершине графа G4 и одновременно
какой-нибудь вершине графа G, не
содержащейся в G4, и имеющего
минимальный вес:
(x1, x5) – вес 5
(x4, x5) – вес 3
(x2, x5) – вес 3
Выбираем из ребер (x4, x5) и (x2, x5) любое
ребро и добавляем его в остовное дерево:
число вершин = 5
Получили минимальное
остовное дерево с весом 7
G4
G5

43. Задача о поиске минимального остовного дерева

43
Задача о поиске минимального остовного дерева
Алгоритм Кра(у)скала
(первый вариант описания):
Исходные данные:
задан связный взвешенный граф G с числом вершин n
Шаг 1:
строим граф T1 = On + e1 , присоединяя к пустому графу (On) на множестве
вершин V(G) ребро e1 E(G) минимального веса
Шаг2:
если граф Ti уже построен и i < n-1, то строим граф Ti+1 = Ti + ei+1 , где ei+1 –
ребро графа G, имеющее минимальный вес среди ребер, не входящих в
Ti и не составляющих циклов с ребрами из Ti
(второй вариант описания): https://brestprog.by/topics/mst/

44. Задача о поиске минимального остовного дерева

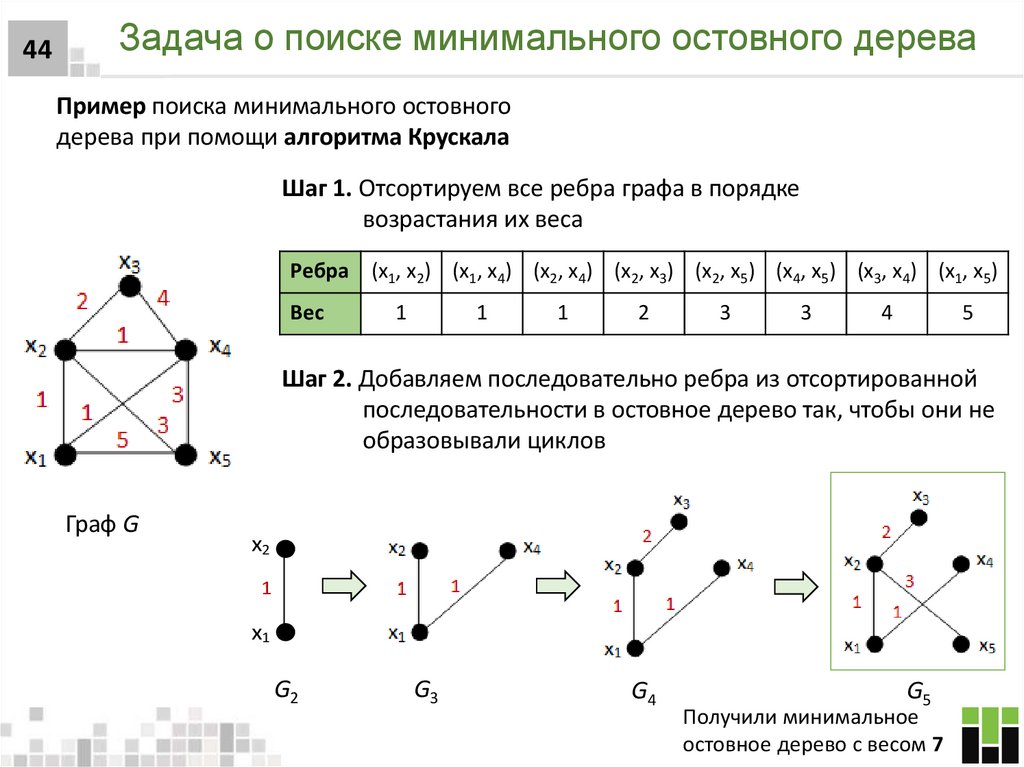
44
Задача о поиске минимального остовного дерева
Пример поиска минимального остовного
дерева при помощи алгоритма Крускала
Шаг 1. Отсортируем все ребра графа в порядке
возрастания их веса
Ребра (x1, x2) (x1, x4) (x2, x4) (x2, x3) (x2, x5) (x4, x5) (x3, x4) (x1, x5)
Вес
1
1
1
2
3
3
4
5
Шаг 2. Добавляем последовательно ребра из отсортированной
последовательности в остовное дерево так, чтобы они не
образовывали циклов
Граф G
x2
1
x1
G2
G3
G4
G5
Получили минимальное
остовное дерево с весом 7

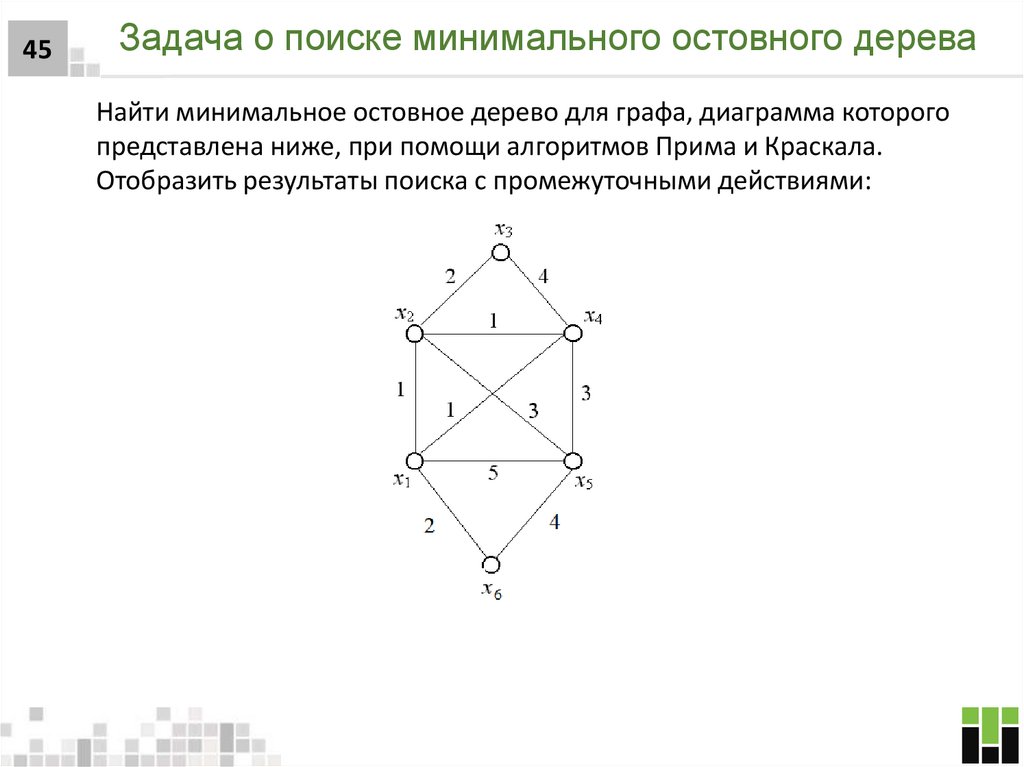
45. Задача о поиске минимального остовного дерева

45
Задача о поиске минимального остовного дерева
Найти минимальное остовное дерево для графа, диаграмма которого
представлена ниже, при помощи алгоритмов Прима и Краскала.
Отобразить результаты поиска с промежуточными действиями: