Загадки пирамиды

1. Загадки пирамиды

ЧЕЛЯБИНСКИЙ МЕХАНИКО-ТЕХНОЛОГИЧЕСКИЙ ТЕХНИКУМ
ЗАГАДКИ ПИРАМИДЫ
Выполнил студент: группы 114 Селянин Данил Андреевич
Г. Челябинск
2025

2. цель проекта: - Исследовать математические закономерности пирамид. - Создать серию загадок и задач на основе их геометрии. -

ЦЕЛЬ ПРОЕКТА:
- ИССЛЕДОВАТЬ МАТЕМАТИЧЕСКИЕ
ЗАКОНОМЕРНОСТИ ПИРАМИД.
- СОЗДАТЬ СЕРИЮ ЗАГАДОК И ЗАДАЧ НА ОСНОВЕ
ИХ ГЕОМЕТРИИ.
- ПОКАЗАТЬ СВЯЗЬ МАТЕМАТИКИ С РЕАЛЬНЫМИ
ОБЪЕКТАМИ.

3. Историческая справка

ИСТОРИЧЕСКАЯ СПРАВКА
• - Кратко о пирамидах: где и когда они были построены.
• - Пример: пирамида Хеопса (высота, основание, возраст).
• - Изображение древних пирамид.

4. Пирамиды Хеопса строили в Нагаде (Абидос) в Верхнем Египте, а также в Саккаре, где находился главный некрополь Мемфиса, столицы

ПИРАМИДЫ
ХЕОПСА
СТРОИЛИ
В НАГАДЕ
(АБИДОС) В
ВЕРХНЕМ ЕГИПТЕ,
А ТАКЖЕ В
САККАРЕ, ГДЕ
НАХОДИЛСЯ
ГЛАВНЫЙ
НЕКРОПОЛЬ
МЕМФИСА,
СТОЛИЦЫ
ПРАВИТЕЛЕЙ
ПЕРВЫХ
ДИНАСТИЙ.
Размер основания
230 м
Высота (первоначально)
146,60 м
Высота (сегодня)
138,75 м
Наклон
51° 50'

5. Геометрия пирамиды

ГЕОМЕТРИЯ ПИРАМИДЫ
- Основные элементы: основание,
грани, вершин
- - Типы пирамид: правильные,
неправильные, усеченные

6. Золотое сечение в пирамидах

ЗОЛОТОЕ СЕЧЕНИЕ В ПИРАМИДАХ
• - Что такое золотое сечение?
• - Как оно проявляется в пропорциях пирамид.
• - Пример: соотношение высоты к половине стороны основания.

7. Золотое сечение

ЗОЛОТОЕ СЕЧЕНИЕ
• Золото́ е сече́ние (золота́я пропо́ рция, иначе: деле́ние в кра́йнем и сре́днем отноше́нии,
гармони́ ческое деление) — отношение частей и целого, при котором отношения частей между
собой и наибольшей части к целому равны. Такие отношения наблюдаются в природе, открыты в
науке и соблюдаются в искусстве. На «золотых отрезках» основываются различные системы и
способы пропорционирования в архитектуре. Соотношение двух величин

8. Углы наклона граней

УГЛЫ НАКЛОНА
ГРАНЕЙ
Как рассчитать угол наклона грани
к основанию.

9. Формула Расчета пирамиды

ФОРМУЛА РАСЧЕТА ПИРАМИДЫ

10. Пример расчета для пирамиды Хеопса.

ПРИМЕР
РАСЧЕТА ДЛЯ
ПИРАМИДЫ
ХЕОПСА.

11. Задача 1 — Объем пирамиды

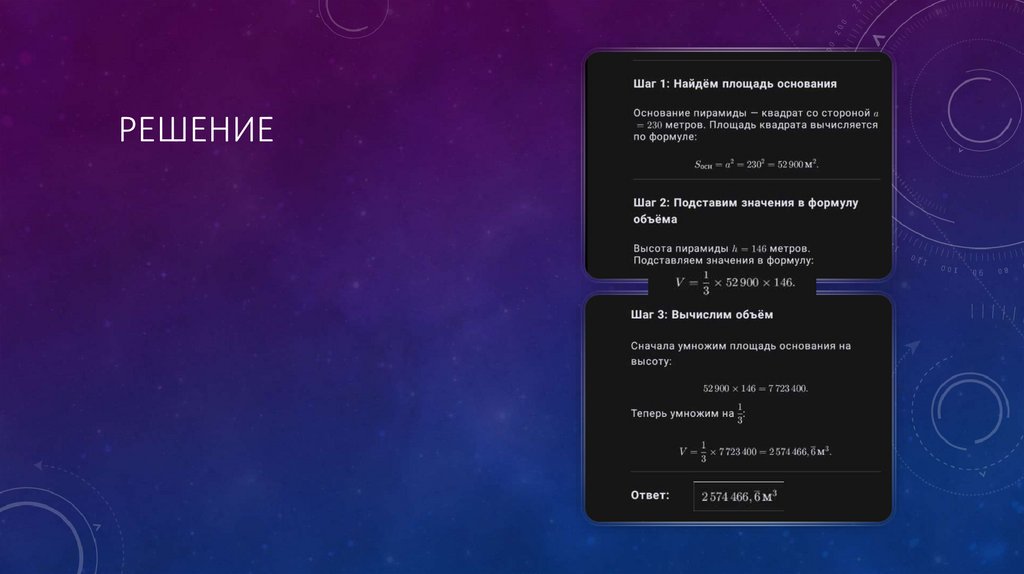
ЗАДАЧА 1 — ОБЪЕМ ПИРАМИДЫ
• - Условие задачи:
"Пирамида имеет квадратное основание со стороной 230 метров и высоту 146 метров. Найдите
ее объем."

12. Решение

РЕШЕНИЕ

13. Задача 2

ЗАДАЧА 2
Угол наклона грани
• - Условие задачи:
"Пирамида имеет высоту 146 метров и длину основания 230 метров. Найдите угол наклона
боковой грани.

14. решение

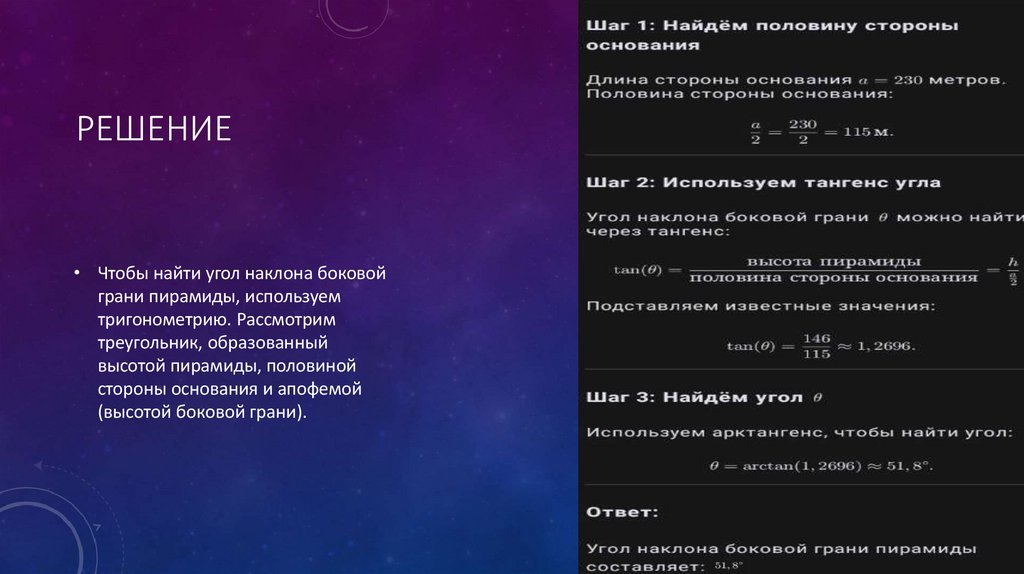
РЕШЕНИЕ
• Чтобы найти угол наклона боковой
грани пирамиды, используем
тригонометрию. Рассмотрим
треугольник, образованный
высотой пирамиды, половиной
стороны основания и апофемой
(высотой боковой грани).

15. Загадка 1

ЗАГАДКА 1
• "Я — фигура с четырьмя треугольными гранями, моя высота относится к стороне основания как 7
к 11. Кто я?"

16. ответ:

ОТВЕТ:
ПИРАМИДА

17. Загадка 2

ЗАГАДКА 2
"Если сложить длину всех ребер пирамиды, получится 920 метров. Сколько метров составляет
длина одного ребра основания?"

18. Ответ: 230 метров.

ОТВЕТ: 230 МЕТРОВ
.

19. Практическая часть

ПРАКТИЧЕСКАЯ ЧАСТЬ
• - Построение модели пирамиды из бумаги.
• - Использование математических расчетов для создания модели.

20. Интересные факты

ИНТЕРЕСНЫЕ ФАКТЫ

21. Пирамиды как инженерное чудо

ПИРАМИДЫ КАК ИНЖЕНЕРНОЕ ЧУДО
• Пирамиды, особенно египетские пирамиды, по праву считаются одним из величайших
инженерных чудес древнего мира. Их строительство демонстрирует невероятные достижения в
области архитектуры, математики и организации труда. Вот несколько аспектов, которые делают
пирамиды инженерным чудом:

22.

• 1. Масштаб и точность строительства
• - Размеры: Великая пирамида Хеопса в Гизе, построенная около 2560 года до н.э., имеет высоту
около 146 метров (сейчас примерно 138 метров из-за потери верхних блоков) и состоит из более
чем 2,3 миллионов каменных блоков, каждый из которых весит в среднем 2,5 тонны.
• - Точность: Пирамиды построены с невероятной точностью. Например, стороны пирамиды Хеопса
ориентированы по сторонам света с отклонением менее 0,15 градуса, что свидетельствует о
глубоких знаниях в астрономии и геометрии.

23.

• 2. Инженерные технологии
• - Транспортировка материалов: Каменные блоки добывались в карьерах, расположенных за
десятки километров от места строительства. Их транспортировка требовала сложной организации
труда и, возможно, использования специальных саней, катков и водных каналов.
• - Подъем блоков: Для подъема многотонных блоков на высоту использовались насыпи, пандусы
и, возможно, примитивные подъемные механизмы. Точные методы до сих пор остаются
предметом исследований.

24.

• 3. Математическая и астрономическая точность
• - Пирамиды отражают глубокие знания древних египтян в математике. Например, соотношение
периметра основания пирамиды Хеопса к её высоте равно 2π, что указывает на понимание числа
π.
• - Ориентация пирамид по сторонам света и их связь с астрономическими явлениями (например, с
положением звёзд) подчеркивают их роль не только как гробниц, но и как символов
космического порядка.

25.

• 4. Долговечность
• - Пирамиды простояли более 4500 лет, выдержав землетрясения, климатические изменения и
воздействие времени. Это свидетельствует о высоком качестве строительства и выборе
материалов.

26.

• 5. Организация труда
• - Строительство пирамид требовало координации труда десятков тысяч рабочих, включая
каменотесов, инженеров, архитекторов и рабочих. Это было возможно благодаря развитой
административной системе Древнего Египта.

27.

• 6. Загадки и теории
• - Несмотря на современные исследования, многие аспекты строительства пирамид остаются
загадкой. Например, как именно достигалась такая точность в обработке и укладке блоков, и
какие инструменты использовались. Это порождает множество теорий, включая гипотезы о
применении неизвестных технологий или даже вмешательстве внеземных цивилизаций.

28.

• Пирамиды — это не только памятники древней архитектуры, но и свидетельство невероятных
инженерных и организационных способностей человечества. Они продолжают вдохновлять
учёных, инженеров и мечтателей по всему миру.

29.

Выводы
- Математика помогает понять структуру пирамид.
- Пирамиды — это не только исторические
памятники, но и объекты для изучения геометрии.
- Проект показал связь математики с реальным
миром.

30. Список литтературы

СПИСОК ЛИТТЕРАТУРЫ
википедия
Ответы mail.com
Яндекс нейро

31. СпАсИбо за внимание!!!!!

СПАСИБО ЗА ВНИМАНИЕ!!!!!