Лекция № 14 Алгоритмы поиска путей

1. Кафедра системы сбора и обработки информации

ВОЕННО-КОСМИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ А.Ф. МОЖАЙСКОГО
Кафедра системы сбора и обработки информации
Дискретная математика
Лекция № 14
Алгоритмы поиска путей
Андрушкевич С.С..

2.

2
Лекция № 14. Алгоритмы поиска путей на графах
Цель: сформулировать основные подходы к построению
маршрутов и изучить подходы к решению оптимизационных задач
на графах по построению кратчайших путей
Учебные вопросы:
1.Алгоритм поиска маршрута (алгоритм Терри)
2.Нахождение кратчайшего пути в сети без контуров (метод
потенциалов)
3.Алгоритм поиска кратчайшего пути (Дейкстры)
4.Алгоритмы поиска всех кратчайших путей (алгоритмы
Флойда, Данцига)

3. Учебный вопрос № 1

1. Алгоритм поиска маршрута
3

4. 1. Алгоритм поиска маршрута

Алгоритм Тэрри
Поиск маршрута в связном графе G (V, Е), соединяющего вершины v и w.
Исходя из вершины v и осуществляя последовательный переход от каждой
достигнутой вершины к смежной ей вершине, всегда можно найти маршрут в
связном графе G (V, Е), соединяющий заданные вершины v и w.
1. При проходе ребра необходимо
всякий раз отмечать направление, в
котором оно было пройдено;
2. Исходя из некоторой вершины v'
нужно всегда следовать по тому
ребру, которое не было пройдено
или
было
пройдено
в
противоположном направлении;
3. Для всякой вершины v', отличной от
v, необходимо отмечать первое
заходящее ребро, если вершина v'
встречается первый раз;
4. Исходя из вершины v', отличной
от v, по первому заходящему в v‘
ребру нужно идти лишь тогда,
когда нет других возможностей.
4

5. 1. Алгоритм поиска маршрута

5
Пример
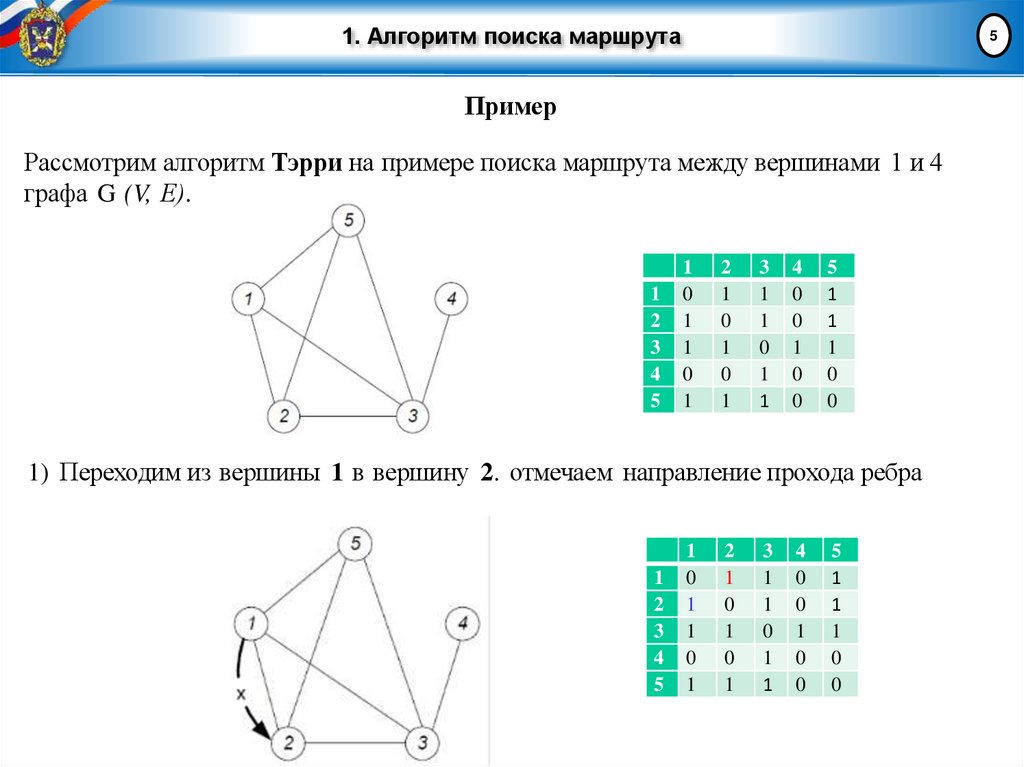
Рассмотрим алгоритм Тэрри на примере поиска маршрута между вершинами 1 и 4
графа G (V, Е).
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0
1) Переходим из вершины 1 в вершину 2. отмечаем направление прохода ребра
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0

6. 1. Алгоритм поиска маршрута

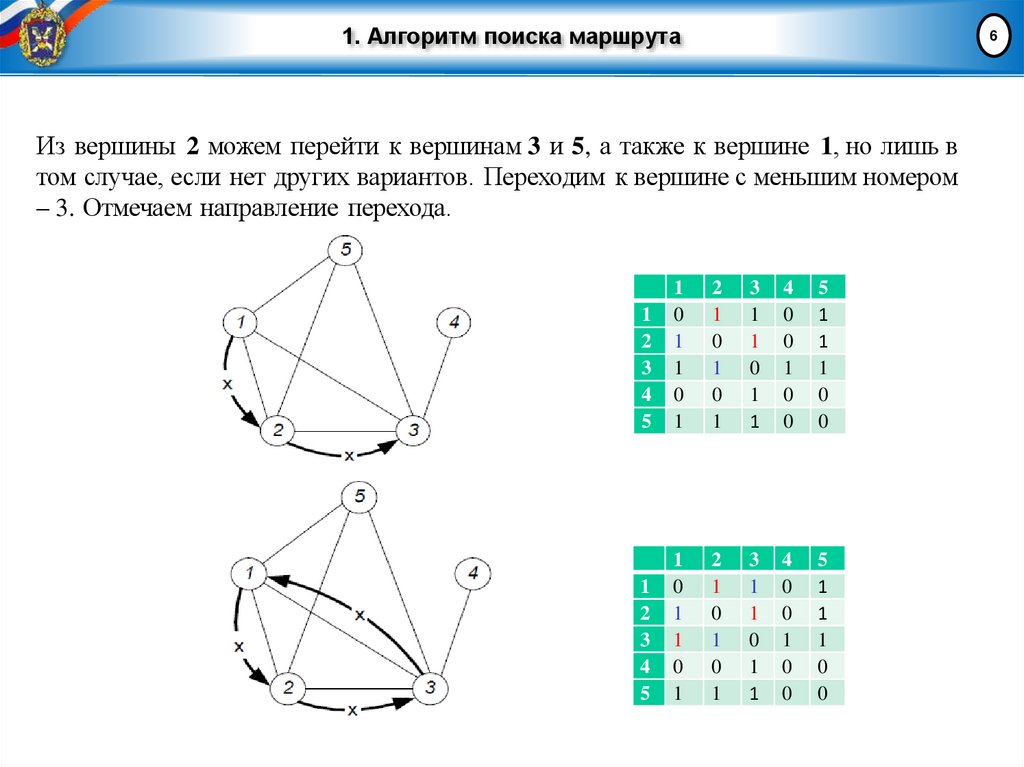
6
Из вершины 2 можем перейти к вершинам 3 и 5, а также к вершине 1, но лишь в
том случае, если нет других вариантов. Переходим к вершине с меньшим номером
– 3. Отмечаем направление перехода.
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0

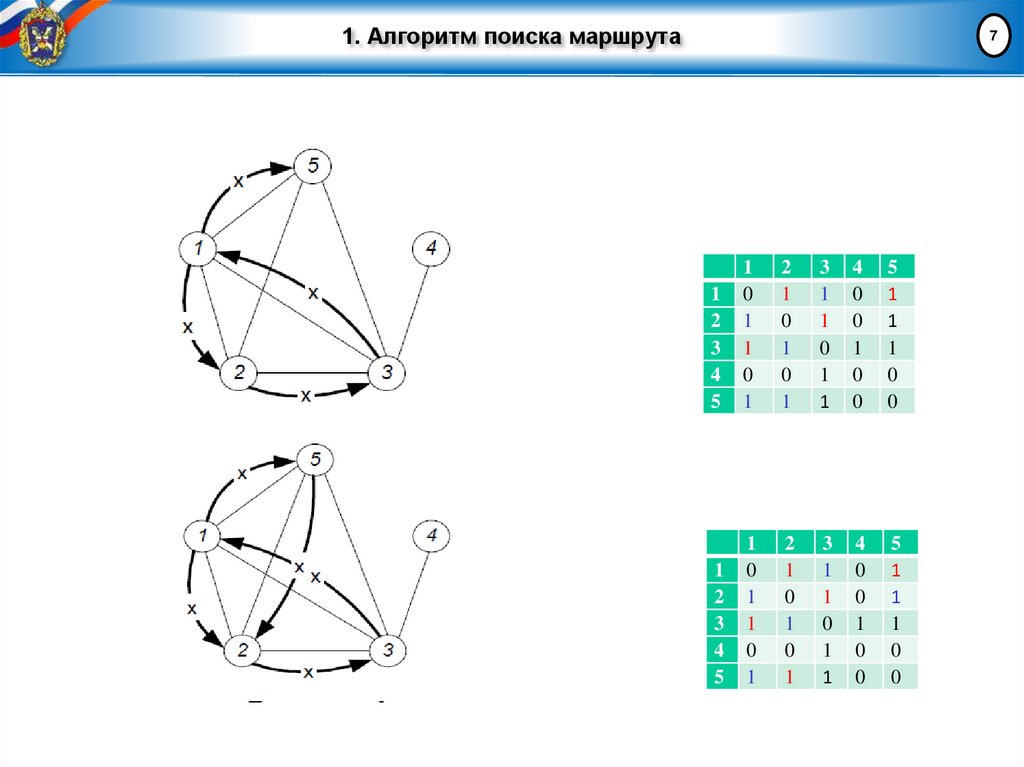
7. 1. Алгоритм поиска маршрута

7
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0

8. 1. Алгоритм поиска маршрута

8
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1
0
0
5
1
1
1
0
0
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
0
1
3
1
1
0
1
1
4
0
0
1!
0
0
5
1
1
1
0
0
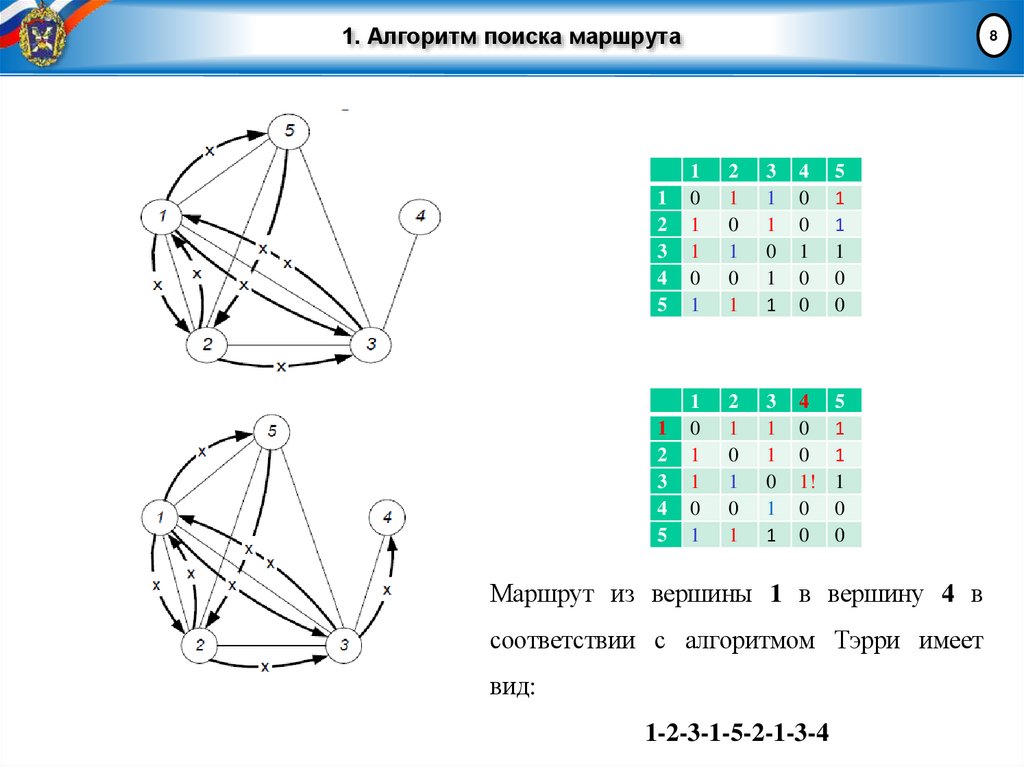
Маршрут из вершины 1 в вершину 4 в
соответствии с алгоритмом Тэрри имеет
вид:
1-2-3-1-5-2-1-3-4

9. Учебный вопрос №2

2. Нахождение кратчайшего пути в сети без контуров
(метод потенциалов)
9

10.

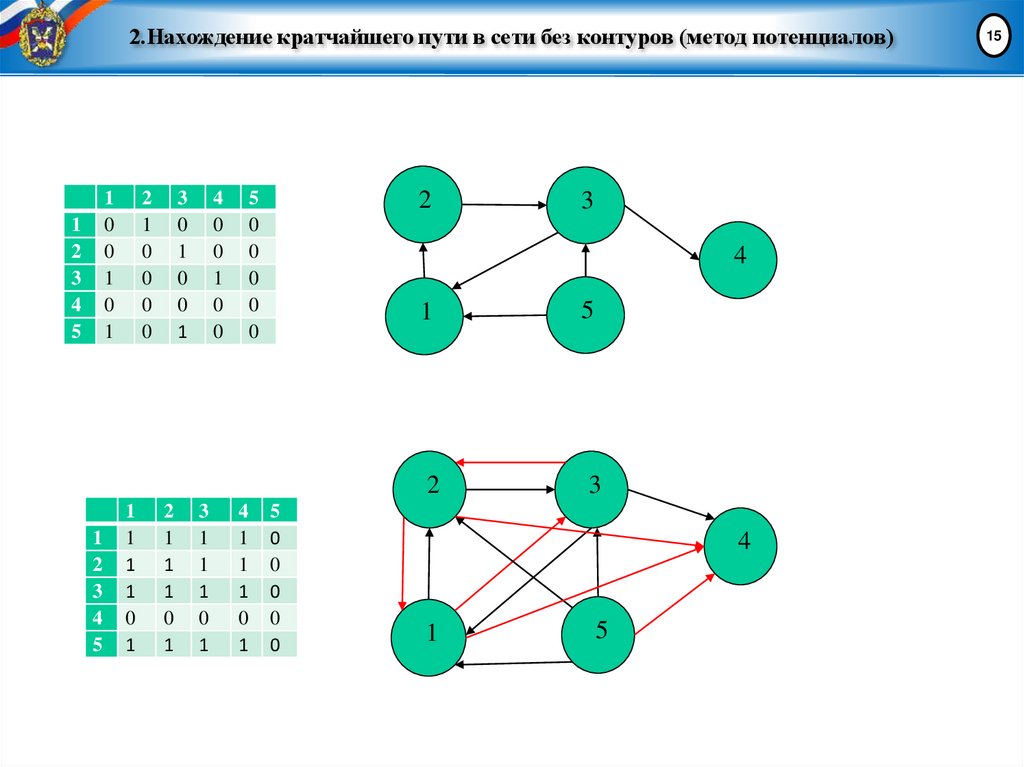
2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)
10
Задана сеть. В ней выделены две вершины – вход и выход. Для каждой дуги
заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма
длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура)
определяется как число входящих в него дуг). Для существования кратчайшего
пути необходимо и достаточно отсутствия в сети контуров отрицательной
длины.
1. Тогда всегда можно пронумеровать
вершины таким образом, что для любой
дуги (i, j) имеет место j > i.
Алгоритм топологической сортировки
Алгоритм вычисления транзитивного
замыкания (Уоршалла)

11. 2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)

Алгоритм построения матрицы достижимости (транзитивного
замыкания) алгоритм Уоршалла
За каждый проход цикла (k) алгоритм Уоршелла генерирует матрицу Wk
используя элементы предыдущей матрицы Wk-1 . Чтобы найти i-ую строку
матрицы Wk следует вычислить выражения: Wk-1(i,j) или (Wk-1(i,k)) и Wk-1(k,j)) (1)
Если Wk-1(i,k) = 0, то (Wk-1(i,k) и Wk-1(k,j)) = 0, и значение (1) совпадает со
значением Wk-1(i,j). Иначе говоря, i-ая строка матрицы остается неизменной.
Если Wk-1(i,k) = 1 вычисление (1) сводится к вычислению (Wk-1(i,k) и Wk-1(k,j)).
При этом i-ая строка получается с помощью логической операции или из текущей
строки i и текущей строки k.
11

12. 2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)

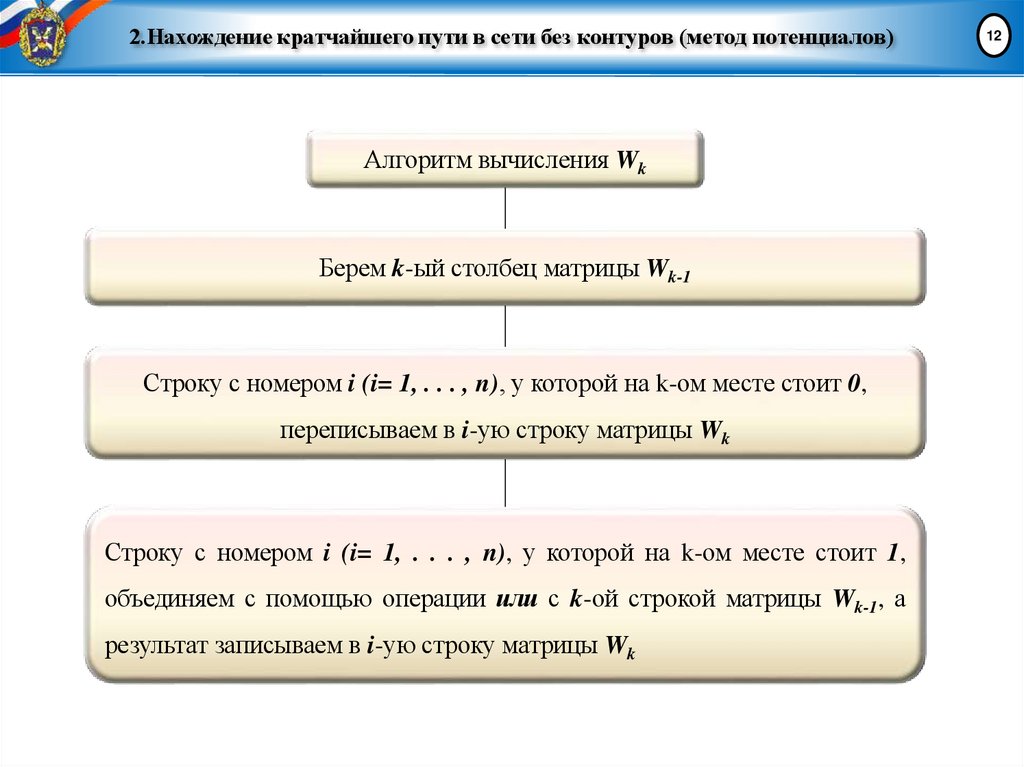
Алгоритм вычисления Wk
Берем k-ый столбец матрицы Wk-1
Строку с номером i (i= 1, . . . , n), у которой на k-ом месте стоит 0,
переписываем в i-ую строку матрицы Wk
Строку с номером i (i= 1, . . . , n), у которой на k-ом месте стоит 1,
объединяем с помощью операции или с k-ой строкой матрицы Wk-1, а
результат записываем в i-ую строку матрицы Wk
12

13. 2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)

2
3
W0
4
1
2
3
4
5
1
0
0
1
0
1
2
1
0
0
0
0
3
0
1
0
0
1
4
0
0
1
0
0
5
0
0
0
0
0
1
2
3
4
5
1
0
0
1
0
1
2
1
0
1
0
1
3
0
1
0
0
1
4
0
0
1
0
0
5
0
0
0
0
0
5
1
W1
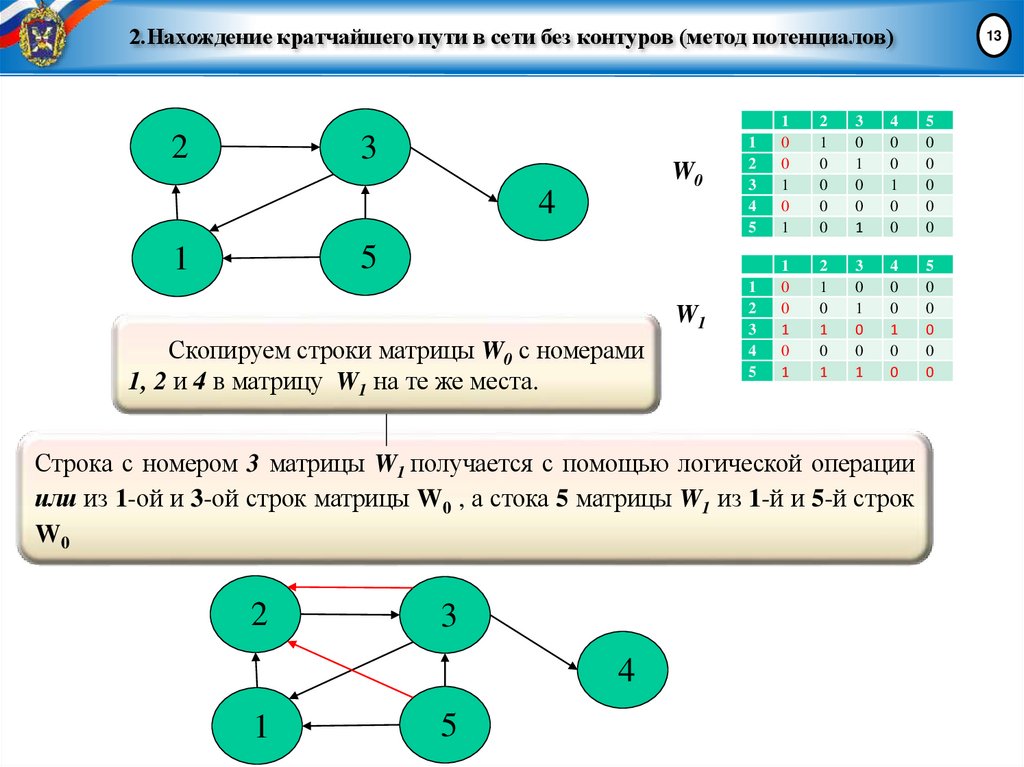
Скопируем строки матрицы W0 с номерами
1, 2 и 4 в матрицу W1 на те же места.
Строка с номером 3 матрицы W1 получается с помощью логической операции
или из 1-ой и 3-ой строк матрицы W0 , а стока 5 матрицы W1 из 1-й и 5-й строк
W0
2
3
4
1
5
13

14. 2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)

1
2
3
4
5
W1
1
2
3
4
5
W2
1
2
3
4
5
W2
W3= 1
2
3
5 4
5
=W
1
0
0
1
0
1
2
1
0
1
0
1
3
0
1
0
0
1
4
0
0
1
0
0
5
0
0
0
0
0
1
2
3
4
5
0
0
1
0
0
0
0
0
0
0
1
0
0
1
0
1
2
1
0
1
0
1
3
1
1
1
0
1
4
0
0
1
0
0
5
0
0
0
0
0
1
1
1
1
0
1
2
1
1
1
0
1
3
1
1
1
0
1
4
1
1
1
0
1
5
0
0
0
0
0
14
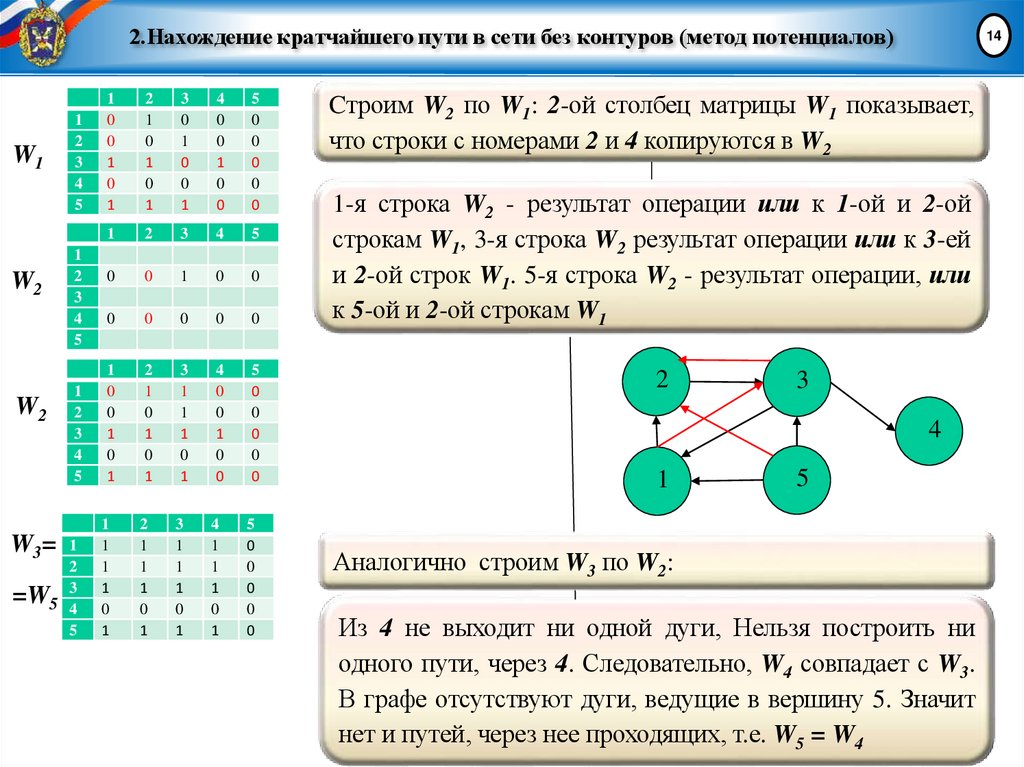
Cтроим W2 по W1: 2-ой столбец матрицы W1 показывает,
что строки с номерами 2 и 4 копируются в W2
1-я строка W2 - результат операции или к 1-ой и 2-ой
строкам W1, 3-я строка W2 результат операции или к 3-ей
и 2-ой строк W1. 5-я строка W2 - результат операции, или
к 5-ой и 2-ой строкам W1
2
3
4
1
5
Аналогично строим W3 по W2:
Из 4 не выходит ни одной дуги, Нельзя построить ни
одного пути, через 4. Следовательно, W4 совпадает с W3.
В графе отсутствуют дуги, ведущие в вершину 5. Значит
нет и путей, через нее проходящих, т.е. W5 = W4

15. 2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)

1
0
0
1
0
1
1
2
3
4
5
1
2
3
4
5
2
1
0
0
0
0
1
1
1
1
0
1
3
0
1
0
0
1
2
1
1
1
0
1
4
0
0
1
0
0
3
1
1
1
0
1
2
5
0
0
0
0
0
4
1
1
1
0
1
3
4
5
0
0
0
0
0
1
5
2
3
4
1
5
15

16.

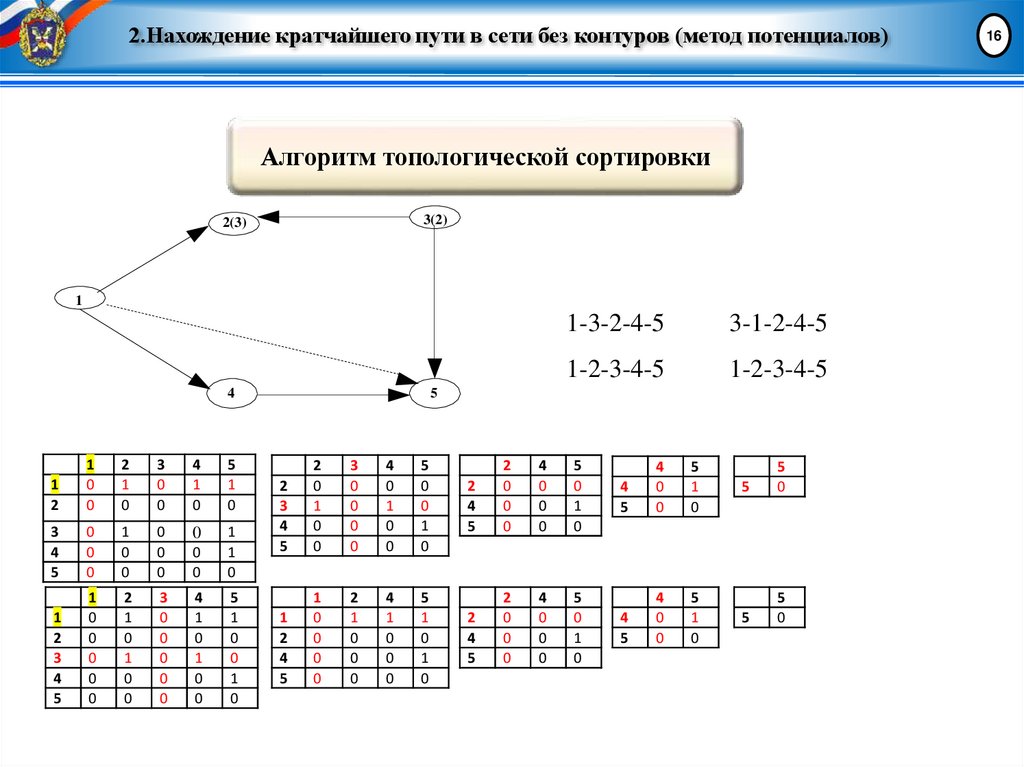
2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)
Алгоритм топологической сортировки
3(2)
2(3)
1
4
1
2
1
0
0
2
1
0
3
0
0
4
1
0
5
1
0
3
4
5
0
0
0
1
0
0
0
0
0
0
0
0
1
1
0
1
2
3
4
5
1
0
0
0
0
0
2
1
0
1
0
0
3
0
0
0
0
0
4
1
0
1
0
0
5
1
0
0
1
0
1-3-2-4-5
3-1-2-4-5
1-2-3-4-5
1-2-3-4-5
5
2
3
4
5
2
0
1
0
0
3
0
0
0
0
4
0
1
0
0
5
0
0
1
0
1
2
4
5
1
0
0
0
0
2
1
0
0
0
4
1
0
0
0
5
1
0
1
0
2
4
5
2
0
0
0
4
0
0
0
5
0
1
0
2
4
5
2
0
0
0
4
0
0
0
5
0
1
0
4
5
4
0
0
5
1
0
4
5
4
0
0
5
1
0
5
5
0
5
5
0
16

17.

2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)
Шаг 0: помечаем нулевую вершину (вход) индексом λ0 = 0;
Шаг k: помечаем вершину k индексом λk = min ( λi + lik ) индексом k
lij – длина дуги (i, j);
λk – потенциал вершины (индекс выхода), равный длине кратчайшего пути.
Кратчайший путь ищется по принципу оптимальности Беллмана:
Если ищется кратчайший путь между двумя точками, то длина пути между
любыми двумя точками кратчайшего пути также должна быть минимальна.
Когда потенциалы установлены, кратчайший путь определяется методом
обратного хода от выхода к входу, то есть кратчайшим является путь, такой, что
ln;n-1 = λn – λn-1
17

18.

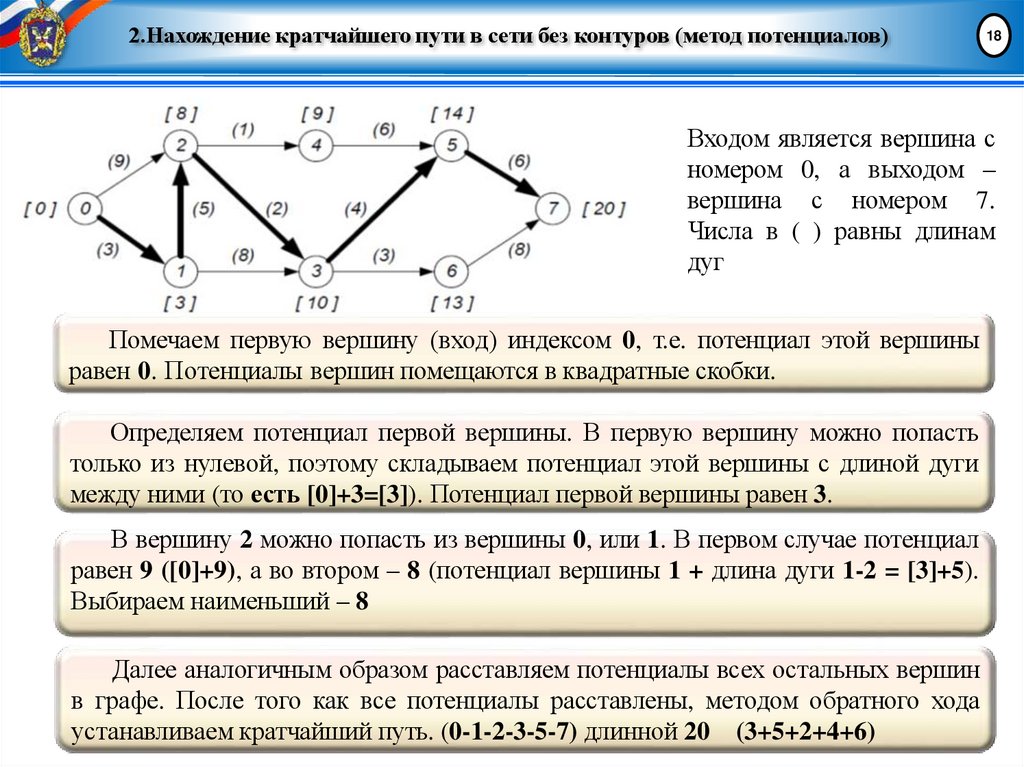
2.Нахождение кратчайшего пути в сети без контуров (метод потенциалов)
18
Входом является вершина с
номером 0, а выходом –
вершина с номером 7.
Числа в ( ) равны длинам
дуг
Помечаем первую вершину (вход) индексом 0, т.е. потенциал этой вершины
равен 0. Потенциалы вершин помещаются в квадратные скобки.
Определяем потенциал первой вершины. В первую вершину можно попасть
только из нулевой, поэтому складываем потенциал этой вершины с длиной дуги
между ними (то есть [0]+3=[3]). Потенциал первой вершины равен 3.
В вершину 2 можно попасть из вершины 0, или 1. В первом случае потенциал
равен 9 ([0]+9), а во втором – 8 (потенциал вершины 1 + длина дуги 1-2 = [3]+5).
Выбираем наименьший – 8
Далее аналогичным образом расставляем потенциалы всех остальных вершин
в графе. После того как все потенциалы расставлены, методом обратного хода
устанавливаем кратчайший путь. (0-1-2-3-5-7) длинной 20 (3+5+2+4+6)

19. Учебный вопрос №3

3. Алгоритм поиска кратчайшего пути
19

20. 3. Алгоритм поиска кратчайшего пути

Каждой дуге (х, у) исходного графа G поставим в соответствие число а(х, у).
Если в графе G отсутствует некоторая дуга (х, у), положим: а(х, у) = ∞. Будем
называть число а(х, у) длиной дуги (х, у). а(х, у) можно интерпретировать как
затраты или некоторый весовой коэффициент. Определим длину пути как
сумму длин отдельных дуг, составляющих этот путь. Для любых двух вершин s
и t графа G могут существовать несколько путей, соединяющих вершину s с
вершиной t. Рассмотрим алгоритм, который определяет путь, ведущий из
вершины s в вершину t, который имеет минимально возможную длину. Этот
путь называется кратчайшим путем между вершинами s и t.
20

21.

3. Алгоритм поиска кратчайшего пути
21
Идея алгоритма Дейкстры
Пусть известны т вершин, ближайших к вершине s.
Пусть известны кратчайшие пути, соединяющие вершину s с выделенными т
вершинами.
Покажем как может быть определена (т+1) ближайшая к s вершина.
Окрасим вершину s и т ближайших к ней вершин (близость любой вершины
х к вершине s определяется длиной кратчайшего пути, ведущего из s в х).
Построим для каждой неокрашенной вершины у пути, непосредственно
соединяющие с помощью дуг (х, у) каждую окрашенную вершину х с у.
Выберем из этих путей кратчайший и будем считать его условно кратчайшим
путем из вершины s в вершину у.

22.

3. Алгоритм поиска кратчайшего пути
22
Ближайшей (т + 1)-й вершиной к s является та, для которой условно
кратчайший путь имеет наименьшую длину.
Это обусловливается тем, что кратчайший путь из вершины s в (т+1)-ю
ближайшую вершину при положительном значении длин всех дуг должен
содержать в качестве промежуточных лишь окрашенные вершины, т. е.
вершины, входящие в число т вершин, ближайших к вершине s.
Начиная с т= 0, описанная процедура может повторяться до тех пор, пока не
будет получен кратчайший путь, ведущий из вершины s к вершине t.

23. 3. Алгоритм поиска кратчайшего пути

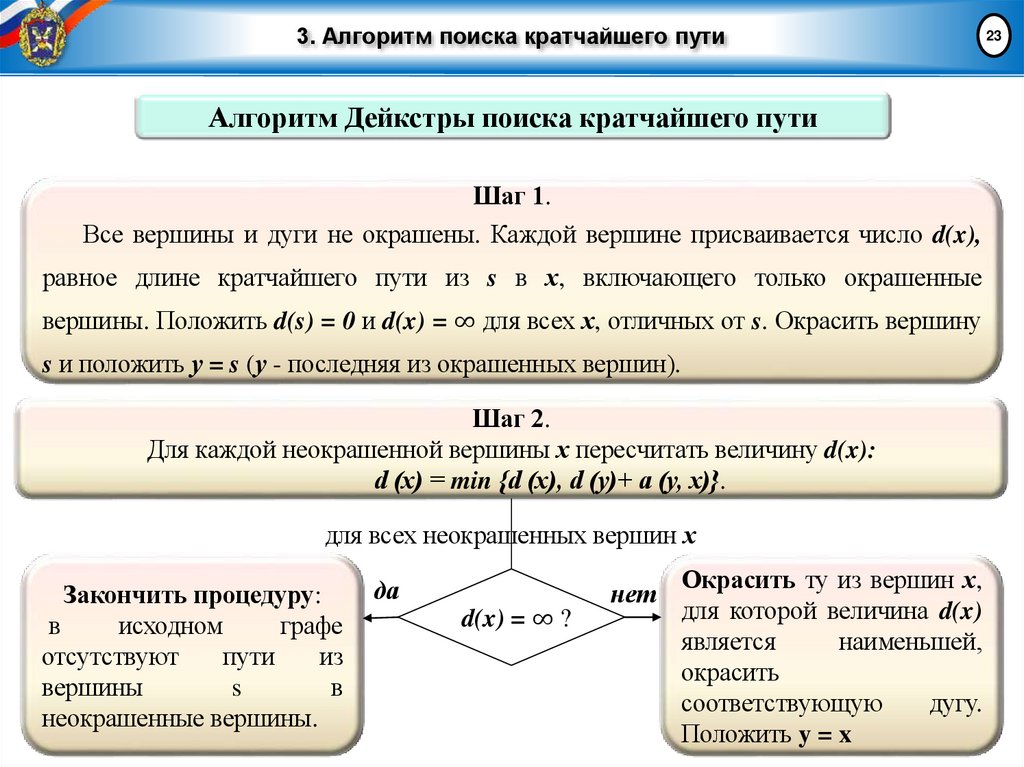
Алгоритм Дейкстры поиска кратчайшего пути
Шаг 1.
Все вершины и дуги не окрашены. Каждой вершине присваивается число d(x),
равное длине кратчайшего пути из s в х, включающего только окрашенные
вершины. Положить d(s) = 0 и d(x) = ∞ для всех х, отличных от s. Окрасить вершину
s и положить у = s (у - последняя из окрашенных вершин).
Шаг 2.
Для каждой неокрашенной вершины х пересчитать величину d(x):
d (х) = min {d (х), d (у)+ а (у, х)}.
для всех неокрашенных вершин х
Закончить процедуру:
в
исходном
графе
отсутствуют
пути
из
вершины
s
в
неокрашенные вершины.
да
d(x) = ∞ ?
нет
Окрасить ту из вершин х,
для которой величина d(x)
является
наименьшей,
окрасить
соответствующую
дугу.
Положить y = x
23

24. 3. Алгоритм поиска кратчайшего пути

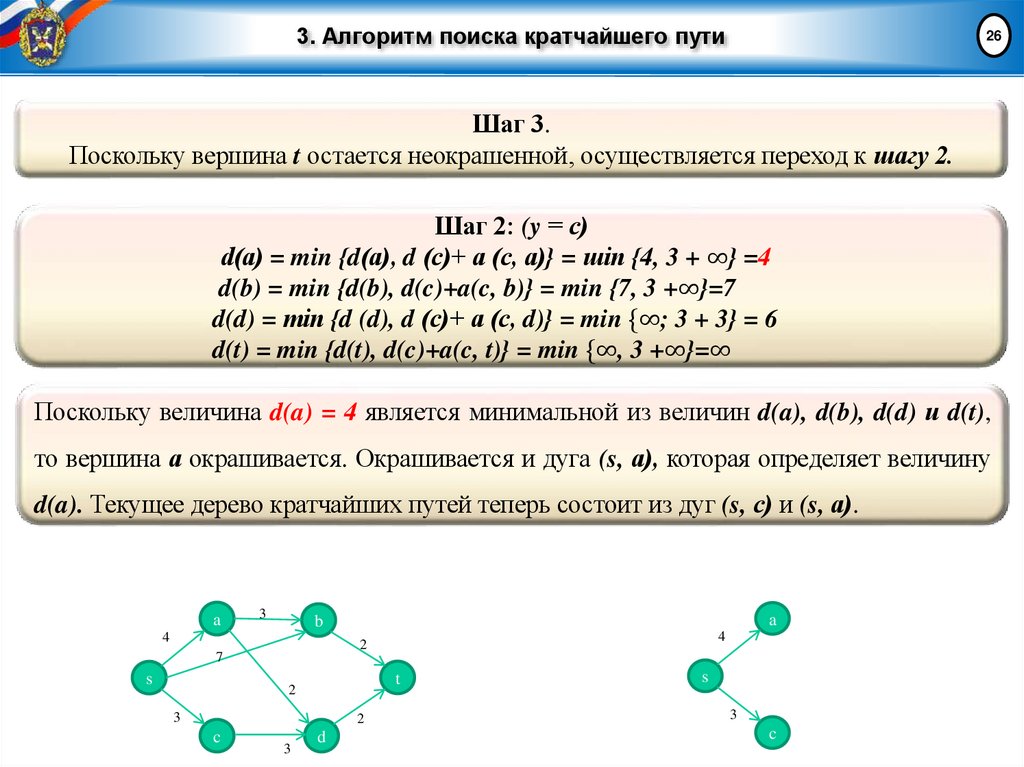
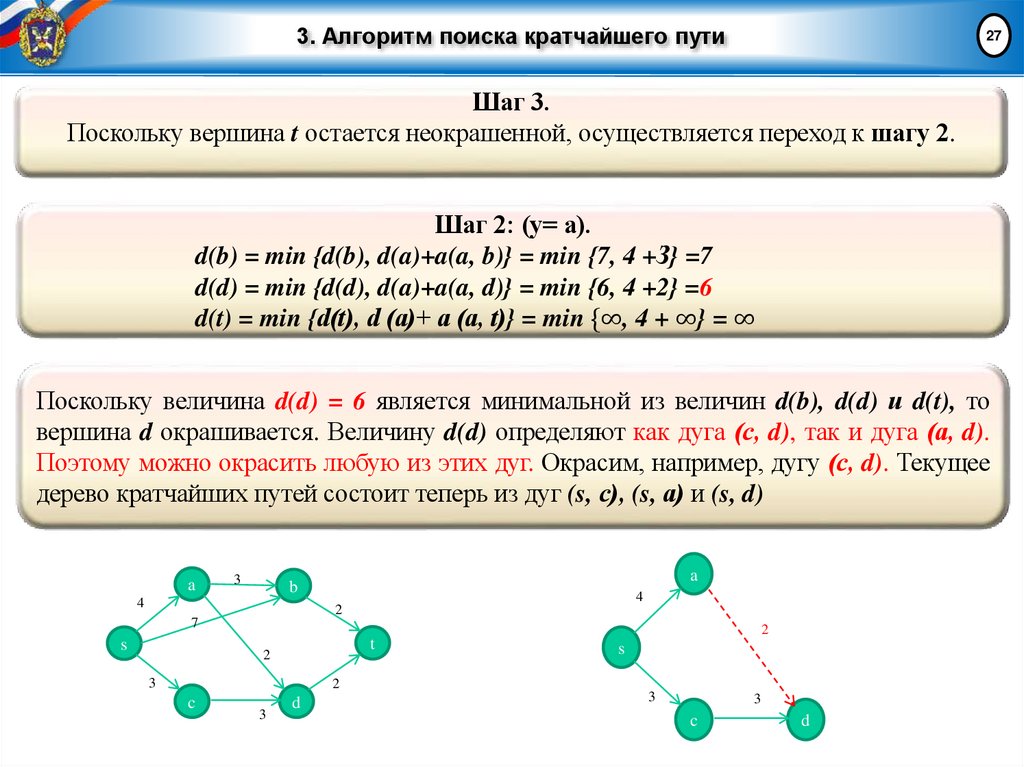
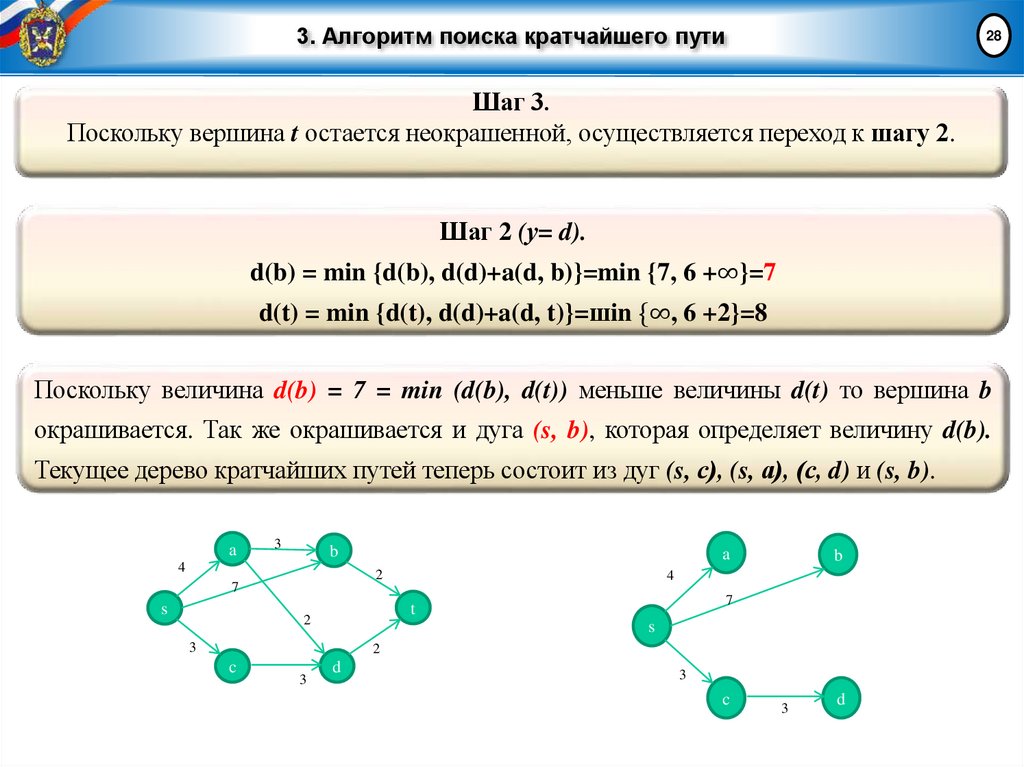
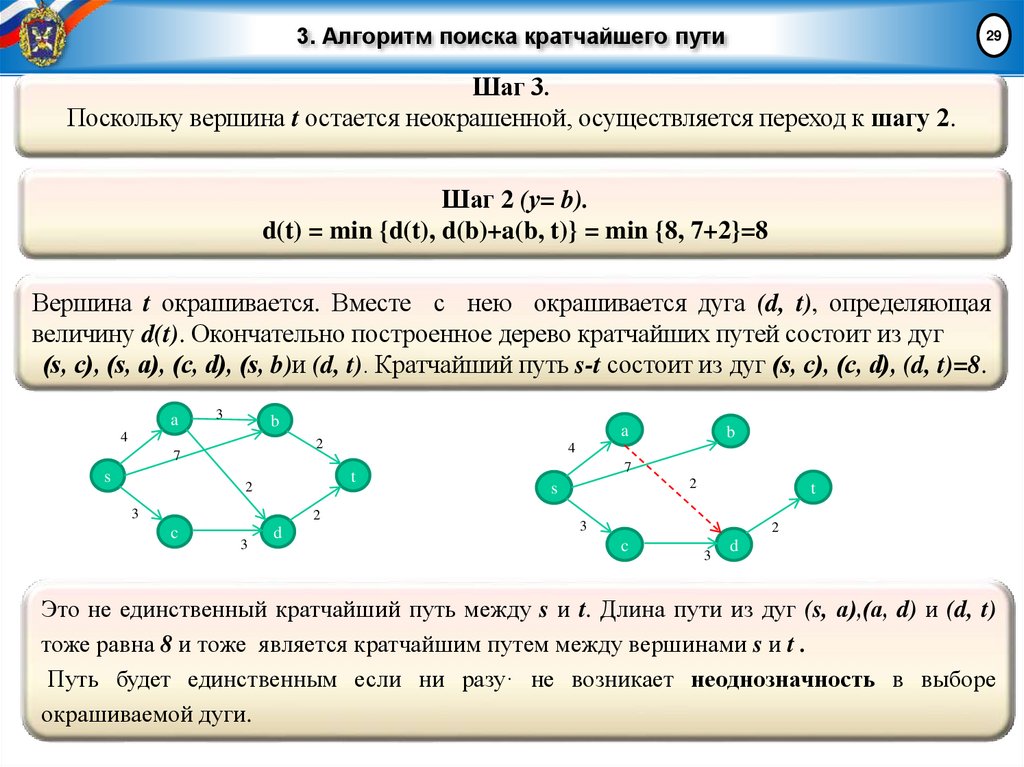
24
Шаг 3.
Если у = t, закончить процедуру; кратчайший путь из вершины s в вершину t найден
(это единственный путь из s в t, составленный из окрашенных дуг). В противном
случае перейти к шагу 2.
Если необходимо определить кратчайшие пути из вершины s во все вершины
исходного графа, то процедуру наращивания дерева следует продолжать до тех пор,
пока все вершины графа не были бы включены в ориентированное дерево кратчайших
путей. При этом для исходного графа было бы получено покрывающее
ориентированное дерево (при условии его наличия).
Чтобы алгоритм позволял получать дерево кратчайших путей от вершины s до всех
остальных вершин, его третий шаг должен быть скорректирован следующим образом:
Шаг 3.
Если все вершины оказываются окрашенными, закончить процедуру (для любой
вершины х имеется единственный путь из s в х, состоящий из окрашенных дуг, и этот
путь является кратчайшим путем между соответствующими вершинами). В
противном случае перейти к шагу 2.

25. 3. Алгоритм поиска кратчайшего пути

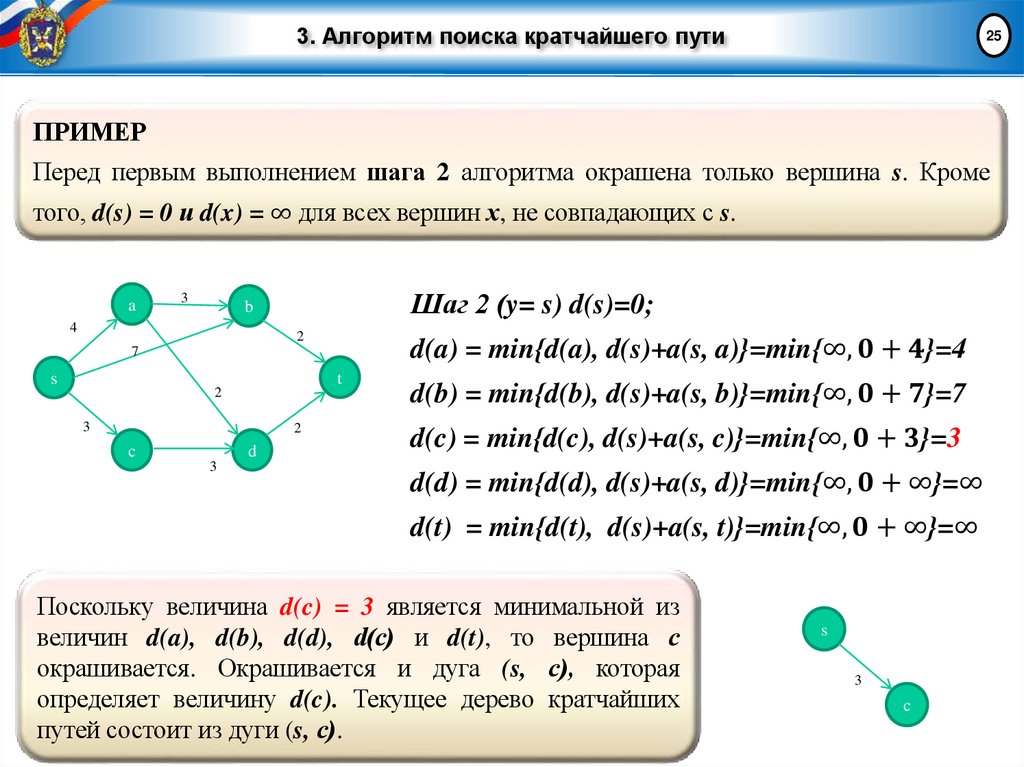
25
ПРИМЕР
Перед первым выполнением шага 2 алгоритма окрашена только вершина s. Кроме
того, d(s) = 0 и d(x) = ∞ для всех вершин х, не совпадающих с s.
a
3
Шаг 2 (y= s) d(s)=0;
b
4
2
d(a) = min{d(a), d(s)+a(s, a)}=min{∞,