Похожие презентации:
Комплексные числа
1. Комплексные числа
ОК 1-5,ОК-8-9
2.
Мы никогда не сталибы разумными, если
бы исключили число
из человеческой
природы.
Платон
3.
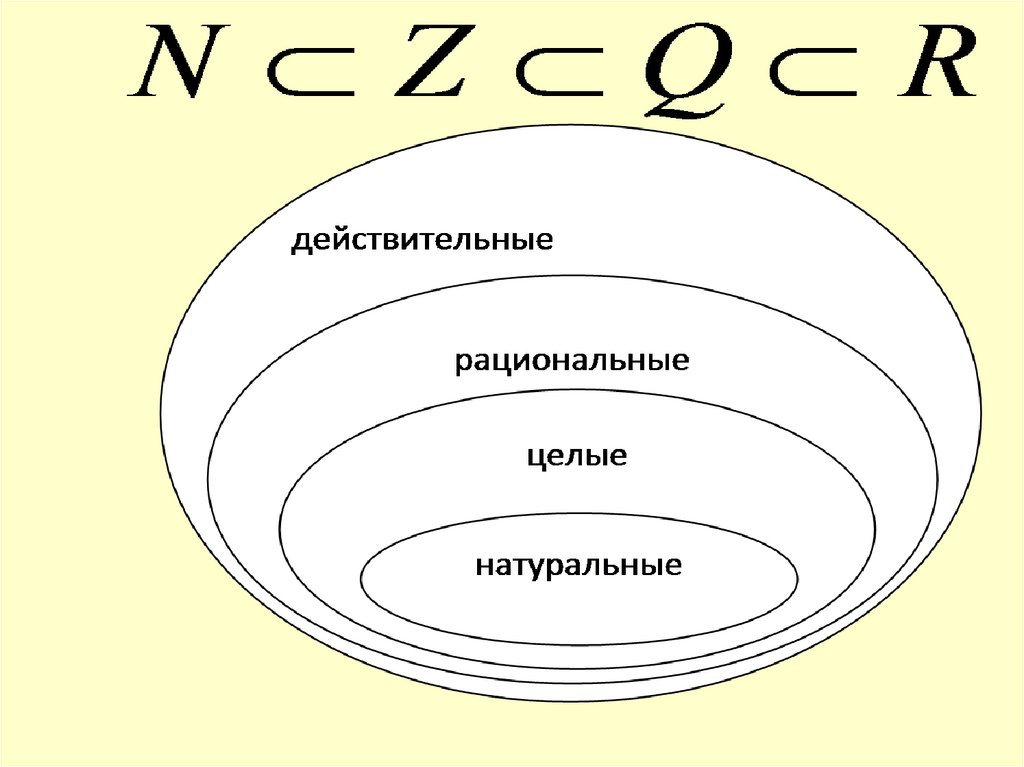
Натуральныечисла
Счет предметов
1, 2, 3…..
N
4.
Целые числах+а=в
…-3,-2,-1,0,1,2,3…
Z
5.
Рациональные числаax = b
…-3, -2,7, -2,-1,0,
2/3,1,2,…
Q
6.
Действительныечисла
…-3, -2,7, -2,1,0, 2/3,1,
,2,…
R
7.
8.
х 1 02
С
9. Мнимая единица
=10.
11.
Джилорамо КорданоРене Декарт
12.
Леонард ЭйлерКарл Гаусс
13. Комплексные числа
Определение 1.Комплексным числом называют число вида
z a bi C a R, b R,
i мнимая единица ,
i 1
a Re z,
b Im z
2
14. Назовите действительную и мнимую части чисел
2 3ii
4 6i
4
3 9i
91i
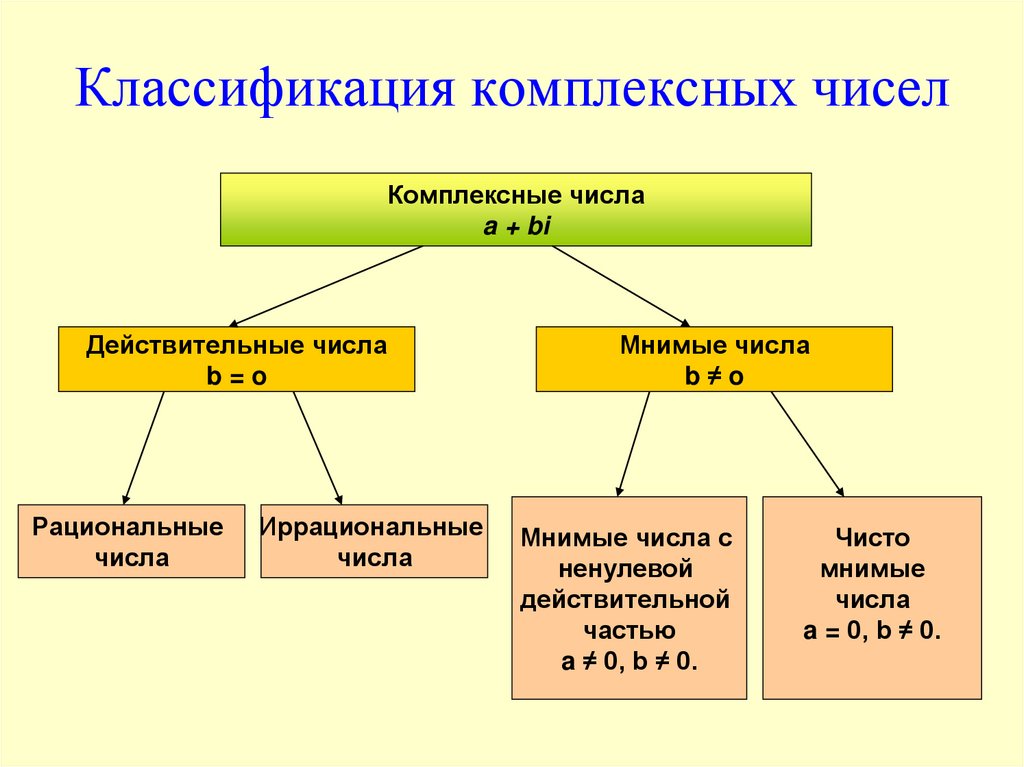
15. Классификация комплексных чисел
Комплексные числаa + bi
Действительные числа
b=o
Рациональные
числа
Иррациональные
числа
Мнимые числа
b≠o
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.
16. Комплексные числа
Определение 2.Два комплексных числа называют
равными, если равны их действительные
части и равны их мнимые части:
a c
a bi c di
b d
17. Мнимые числа
i2 = -1,i – мнимая единица
i, 2i, -0, 3i — чисто мнимые числа
Арифметические операции над чисто
мнимыми числами
3i 13i 3 13 i 16i
3i 13i 3 13 i i 39i
i
7
i i
i
2
3
2
39
18. Мнимые числа
В общем виде правила арифметическихопераций с чисто мнимыми числами таковы:
ai bi a b i;
ai bi a b i;
a bi ab i;
ai bi abi ab
2
где a и b — действительные числа.
19. Сопряженные комплексные числа
Определение:Если у комплексного числа сохранить
действительную часть и поменять знак у мнимой
части, то получится комплексное число,
сопряженное данному.
Если данное комплексное число обозначается
буквой Z, то сопряженное число обозначается
z :
z x yi z x yi
20. Сопряженные комплексные числа
Из всех комплексных чиселдействительные числа (и только они)
равны своим сопряженным числам.
Числа a + bi и a - bi называются
взаимно сопряженными комплексными
числами.
21. Свойства сопряженных чисел
1. Сумма и произведение двух сопряженных чиселесть число действительное.
z z ( a bi ) ( a bi ) 2a
z z ( a bi )( a bi ) a (bi ) a b
2
2
2
2
2. Число, сопряженное сумме двух комплексных
чисел, равно сумме сопряженных данным
числам.
z1 z2 z1 z2
3. Число, сопряженное разности двух комплексных
чисел, равно разности сопряженных данным
числам.
z1 z2 z1 z2
22. Свойства сопряженных чисел
4. Число, сопряженное произведению двухкомплексных чисел, равно произведению
сопряженных данным числам.
z1z2 z1 z2
5. Число, сопряженное п-ой степени комплексного
числа z, равно п-ой степени числа,
сопряженного к числу z, т.е.
n
n
z ( z) , n N
6. Число, сопряженное частному двух
комплексных чисел, из которых делитель
отличен от нуля, равно частному
сопряженных чисел, т.е.
a bi a bi
c di c di
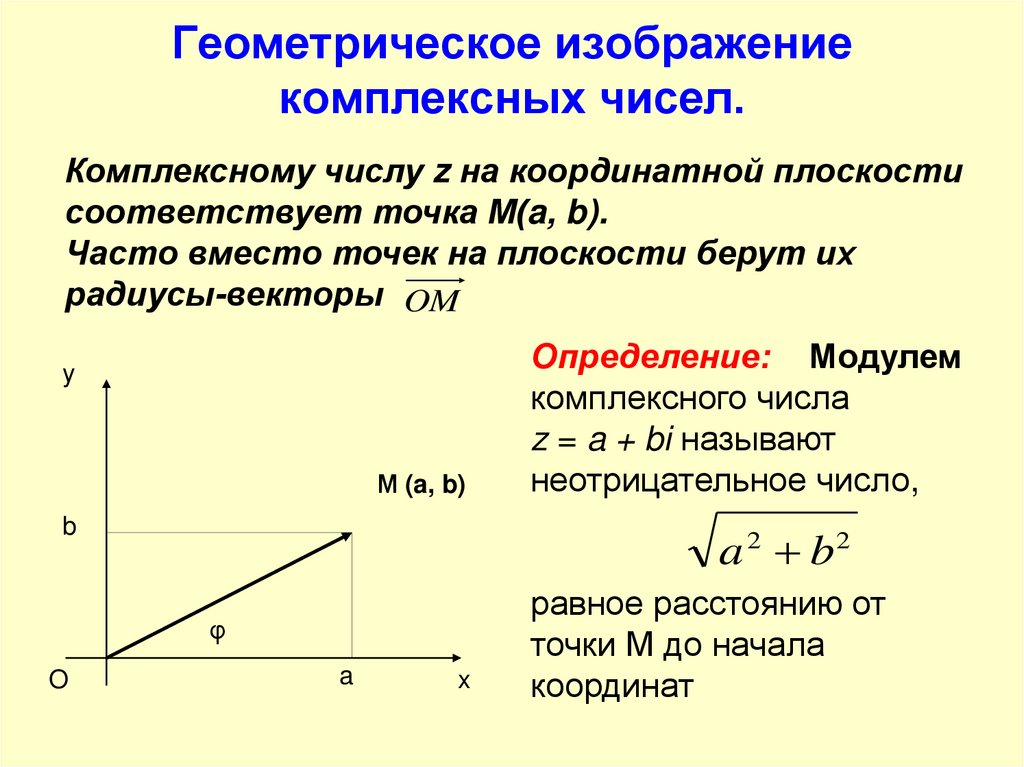
23. Геометрическое изображение комплексных чисел.
Комплексному числу z на координатной плоскостисоответствует точка М(a, b).
Часто вместо точек на плоскости берут их
радиусы-векторы OM
y
М (a, b)
b
a 2 b2
φ
O
Определение: Модулем
комплексного числа
z = a + bi называют
неотрицательное число,
a
x
равное расстоянию от
точки М до начала
координат
24. Геометрическое изображение комплексных чисел.
yГеометрическое изображение
комплексных чисел.
М (a, b)
b
φ
O
a
cos
x
a
z a b
и sin
2
b
a b
a b
аргумент комплексно го числа
;
2
2
2
2
2
25. Арифметические операции над комплексными числами
(а + bi) + (c + di) = (а + с) + (b + d)i(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)( c di) ac bd bc ad
2
2
i
2
2
c di (c di)( c di) c d
c d
26. Степени мнимой единицы
По определению первой степенью числа iявляется само число i, а второй степенью –
число
-1:
1
1
2
i = i, i = -1
.
Более высокие степени числа i находятся следующим
образом:
4
3
2
i = i ∙ i = -∙i = 1;
i5 = i4 ∙ i = i;
i6 = i5 ∙ i = i2= - 1 и т.д.
Очевидно, что при любом натуральном n
i4n = 1;
i4n +2 = - 1
i4n+1 = i;
i4n+3 = - i.
27. Извлечение квадратных корней из комплексных чисел в алгебраической форме.
• Определение. Число w называют квадратным корнем из2
комплексного числа z, если его квадрат равен z: w z
• Теорема. Пусть z=a+bi – отличное от нуля комплексное число.
Тогда существуют два взаимно противоположных комплексных
числа, квадраты которых равны z. Если b≠0, то эти два числа
выражаются формулой:
w
a2 b2 a
i signb
2
a 2 b 2 a
, где
2
1, если b 0
signb 1, если b 0
0, если b 0
При b 0, a 0 имеем : w a , при b 0, a 0 имеем : w i a .
28. Тригонометрическая форма комплексного числа
z r cos i sinгде φ – аргумент комплексного числа,
r = a 2 b 2 - модуль комплексного числа,
cos
a
a2 b2
и sin
b
a2 b2
29. Умножение и деление комплексных чисел, заданных в тригонометрической форме
Теорема1.
Если z 0, z 0
1
2
и
z1 r1 cos 1 i sin 1 , z2 r2 cos 2 i sin 2 , то:
а)
б)
z1 z2 r1r2 cos 1 2 i sin 1 2
z1 r1
cos 1 2 i sin 1 2
z2 r2
30.
Теорема 2 (формула Муавра)Пусть z — любое отличное от
нуля комплексное число, п — любое
целое число. Тогда
z r cos n i sin n
n
n
31. Извлечение корня из комплексного числа
• Теорема. Для любого натурального числа n иотличного от нуля комплексного числа z
существуют n различных значений корня n-ой
степени.
Если z r cos i sin ,
выражаются формулой
то эти значения
2 k
2 k
wk r cos
i sin
,
n
n
где k 0,1,..., (n 1)
n






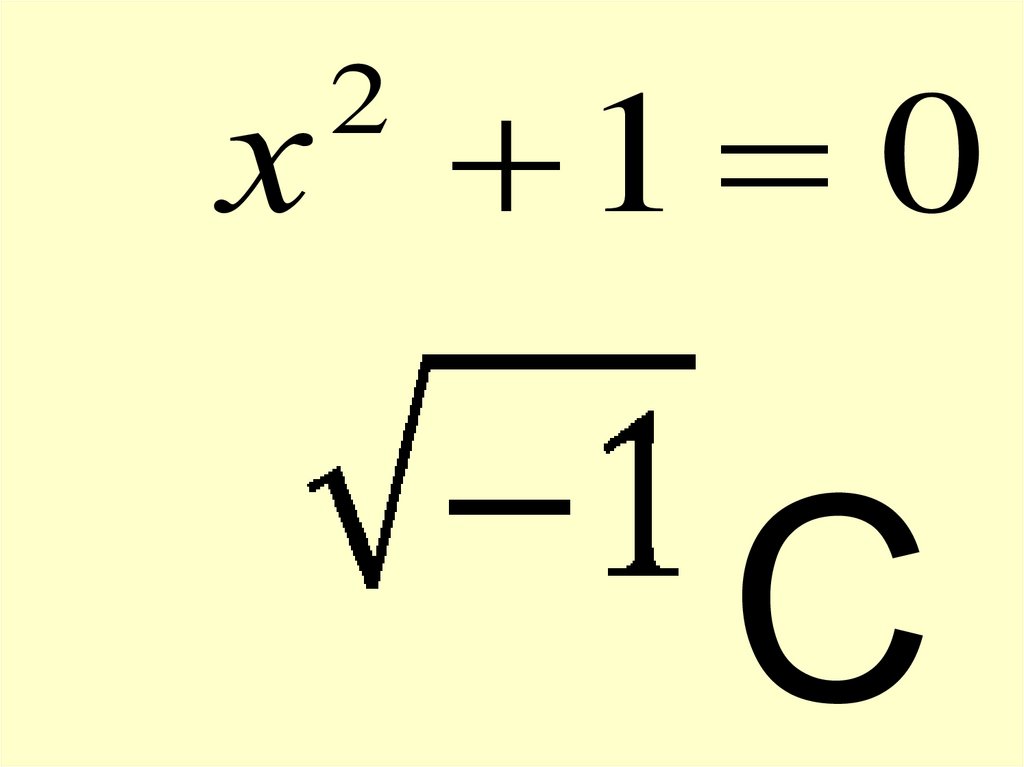
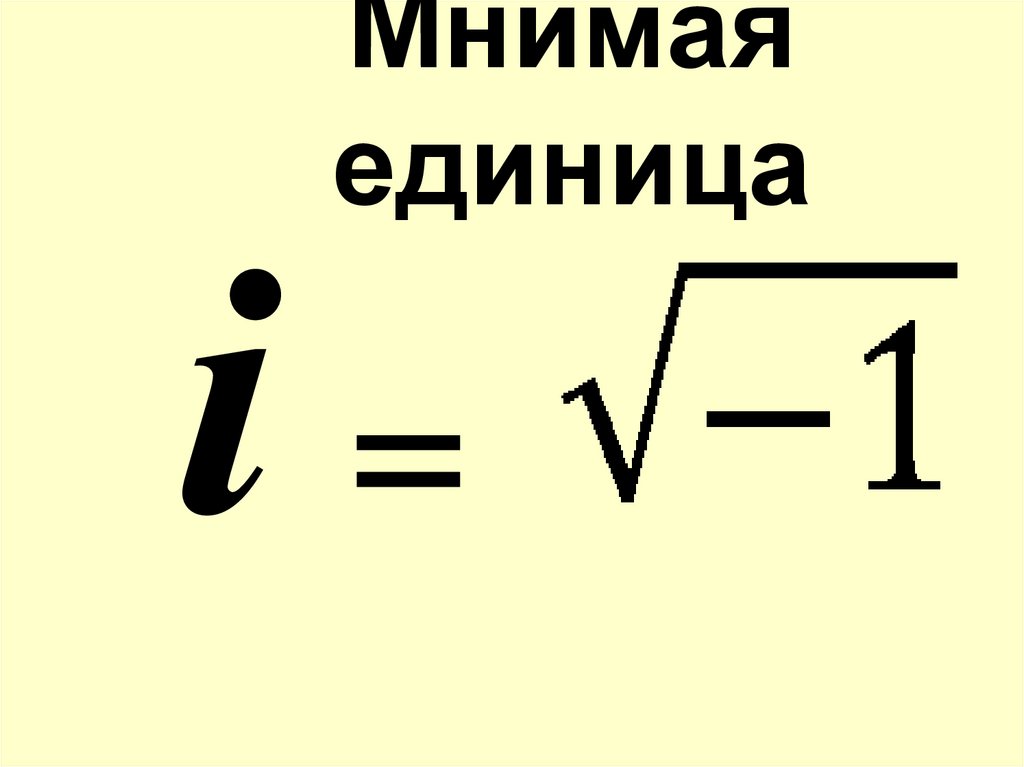
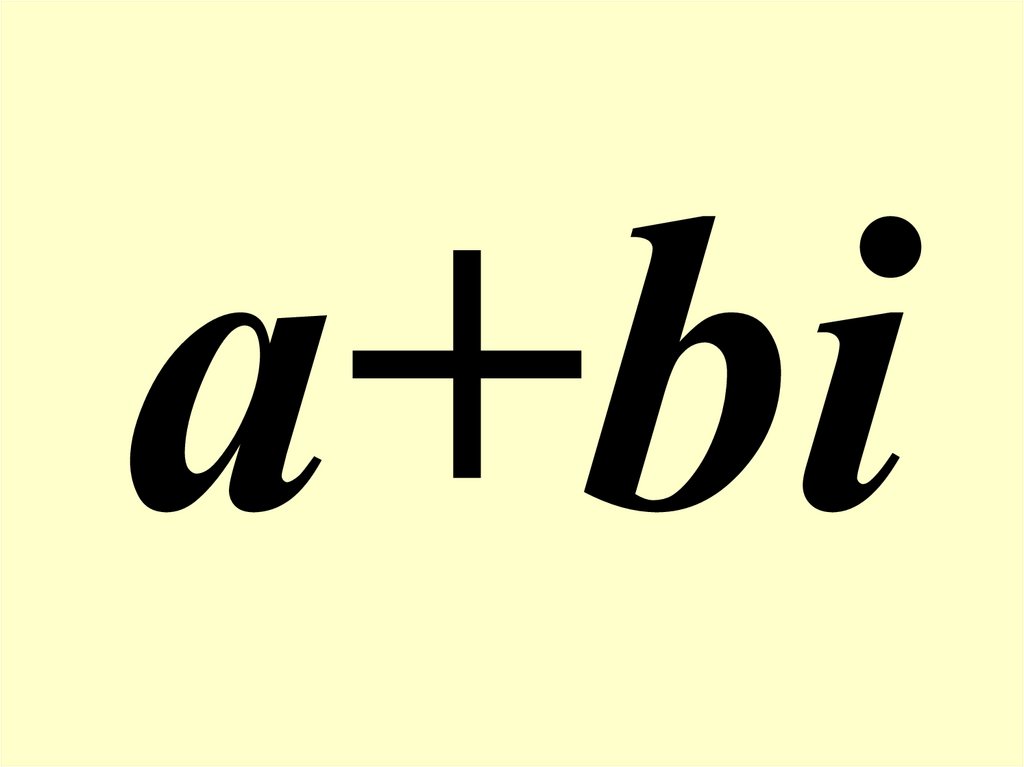



















 Математика
Математика








