Лекция 9 Отображения и функции

1.

ВОЕННАЯ АКАДЕМИЯ ВОЗДУШНО-КОСМИЧЕСКОЙ ОБОРОНЫ
имени МАРШАЛА СОВЕТСКОГО СОЮЗА Г.К. ЖУКОВА
Кафедра основ построения радиоэлектронных средств и систем
Учебная дисциплина ДС-133
«Дискретная математика»
Тверь 2023

2.

Содержание темы № 2
«Множества и операции над множествами»
Номера и вид
занятий
Лекция № 8
Наименование тем занятий
Основные понятия теории множеств.
Решение задач на aнализ множеств и
выполнение операций над ними.
Лекция № 9 Отображения и функции
Решение задач на анализ функций и
Пр. зан. № 9 исследование
множеств
на
счетность,
несчетность
Пр. зан. № 8

3.

Лекция № 9
ОТОБРАЖЕНИЯ
И ФУНКЦИИ

4.

ПРОФЕССИОНАЛЬНАЯ КОМПЕТЕНЦИЯ
Способен использовать положения, законы и методы
естественных наук и математики для решения задач
инженерной деятельности (ОПК-1).
ЗНАТЬ: основные понятия, методы и алгоритмы
дискретной математики
УЧЕБНАЯ ЦЕЛЬ ЛЕКЦИИ
Дать систематизированные основы научных знаний по
теории множеств, рассмотрев понятия отображения и
мощности множеств, типы отображений множеств,
равномощные, счетные и несчетные множества; а также
понятие функции как отображения двух множеств.

5.

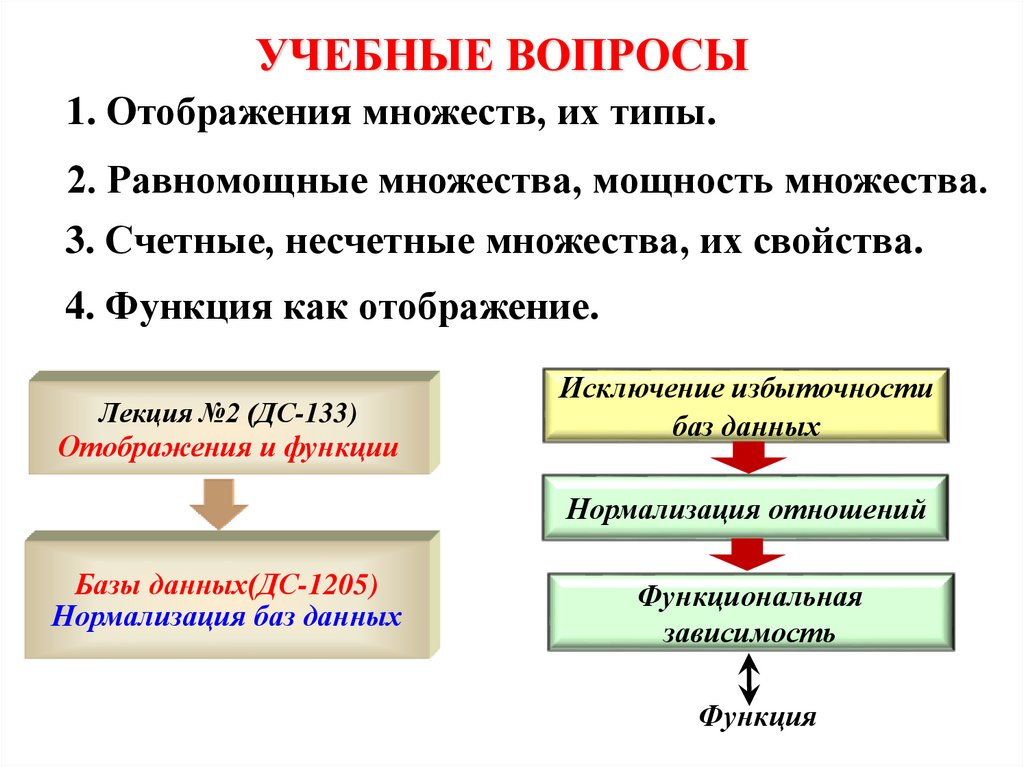
УЧЕБНЫЕ ВОПРОСЫ
1. Отображения множеств, их типы.
2. Равномощные множества, мощность множества.
3. Счетные, несчетные множества, их свойства.
4. Функция как отображение.
Лекция №2 (ДС-133)
Отображения и функции
Моделирование и проектирование
АСОИУ (ДС-811)
Основные категории измерений
Шкала
< M, N, f >
отображение

6.

УЧЕБНЫЕ ВОПРОСЫ
1. Отображения множеств, их типы.
2. Равномощные множества, мощность множества.
3. Счетные, несчетные множества, их свойства.
4. Функция как отображение.
Лекция №2 (ДС-133)
Отображения и функции
Исключение избыточности
баз данных
Нормализация отношений
Базы данных(ДС-1205)
Нормализация баз данных
Функциональная
зависимость
Функция

7.

ЛИТЕРАТУРА
л.1/о
Восканян
А.Б.
Дискретная
Уч. пособие. – Тверь; ВА ВКО, 2019.
математика:
л. 2/о (Э) Восканян А.Б. Дискретная математика
[Электронный ресурс]: Учебное пособие.– Тверь;
ВА ВКО, 2016. URL: http://ibook.academy.org/book/77.
л.1/д Новиков Ф.А. Дискретная математика: Учебник
для вузов. 2-е изд – СПб : Питер, 2014
Сервер академии: учебные пособия\13 кафедра\ДС-133\
дополнительная литература\Новиков.pdf

8.

9.

1. ОТОБРАЖЕНИЯ
МНОЖЕСТВ, ИХ ТИПЫ.

10.

ОТОБРАЖЕНИЕ
▪ Отображение f – это правило, которое каждому
элементу х Х ставится в соответствие элемент y Y.
Обозначение :
f : X→Y.
Х – область определения;
У – область значений.
X – множество курсантов в аудитории,
У – множество столов в аудитории
f: X→Y «курсант х сидит за столом у»
элемент х – прообраз
элемент y – образ элемента х
множество f(Х) – образ множества Х

11.

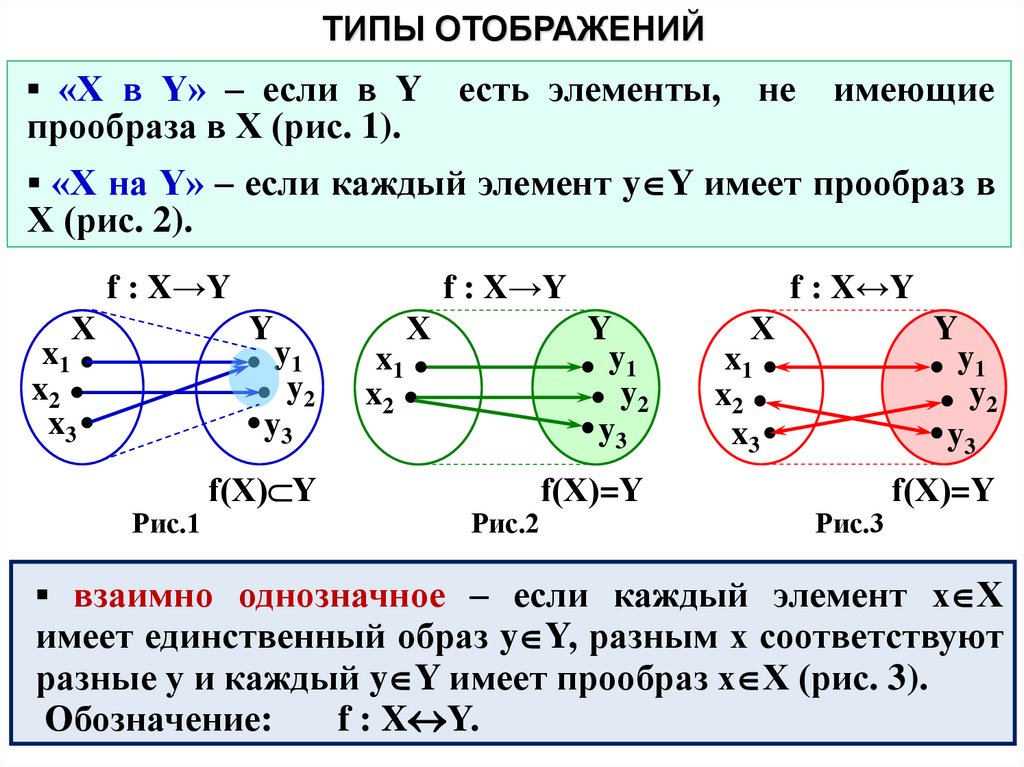
ТИПЫ ОТОБРАЖЕНИЙ
▪ «X в Y» – если в Y есть элементы,
прообраза в Х (рис. 1).
не
имеющие
▪ «X на Y» – если каждый элемент y Y имеет прообраз в
Х (рис. 2).
f : X→Y
Х
f : X→Y
Y
y1
y2
y3
x1
x2
x3
Рис.1
f(Х) Y
x1
x2
Х
f : X↔Y
Y
y1
y2
y3
Рис.2
f(Х)=Y
Х
Y
y1
y2
y3
x1
x2
x3
Рис.3
f(Х)=Y
▪ взаимно однозначное – если каждый элемент х Х
имеет единственный образ y Y, разным х соответствуют
разные у и каждый y Y имеет прообраз х Х (рис. 3).
Обозначение:
f : X Y.

12.

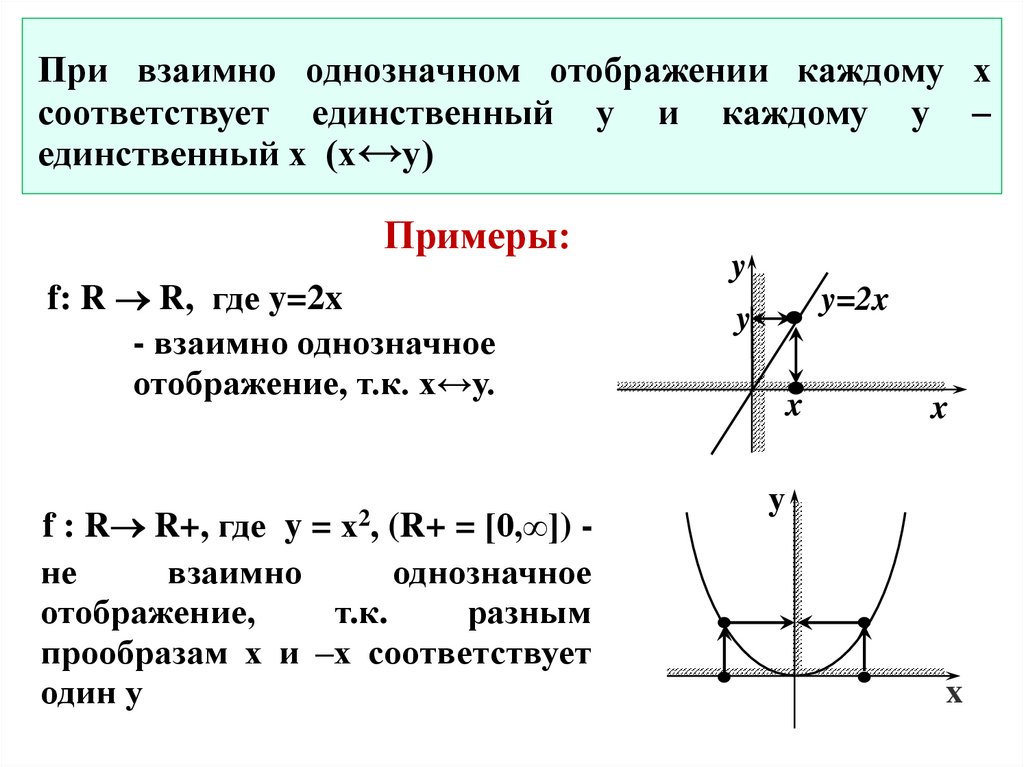
При взаимно однозначном отображении каждому х
соответствует единственный у и каждому у –
единственный х (х↔у)
Примеры:
f: R R, где y=2x
- взаимно однозначное
отображение, т.к. х↔у.
y = х2, (R+ = [0,∞]) -
f : R R+, где
не
взаимно
однозначное
отображение,
т.к.
разным
прообразам х и –х соответствует
один у
y
y=2x
y
x
x
y
x

13.

Выводы по первому вопросу
Понятие отображения является одним
из фундаментальных понятий теории
множеств.
Основными
типами
отображений
являются отображения Х в Y, Х на Y и
взаимно однозначное отображение.
13

14.

2. РАВНОМОЩНЫЕ МНОЖЕСТВА,
МОЩНОСТЬ МНОЖЕСТВА,

15.

▪ Множества А и В называют равномощными
если между ними можно установить
однозначное отображение (соответствие).
(А~В),
взаимно
Мощность множества – это общее свойство, которое есть
у всех равномощных множеств.
|А| – мощность множества А
Если А~В, то |А| = |В|.
▪ Мощность конечного множества равна числу его
элементов.
А – русский алфавит,
|А|= 33
В – мн-во времен года,
|В|= 4
Ø
| Ø |= 0
▪ Под мощностью бесконечного множества понимают
запас его элементов.

16.

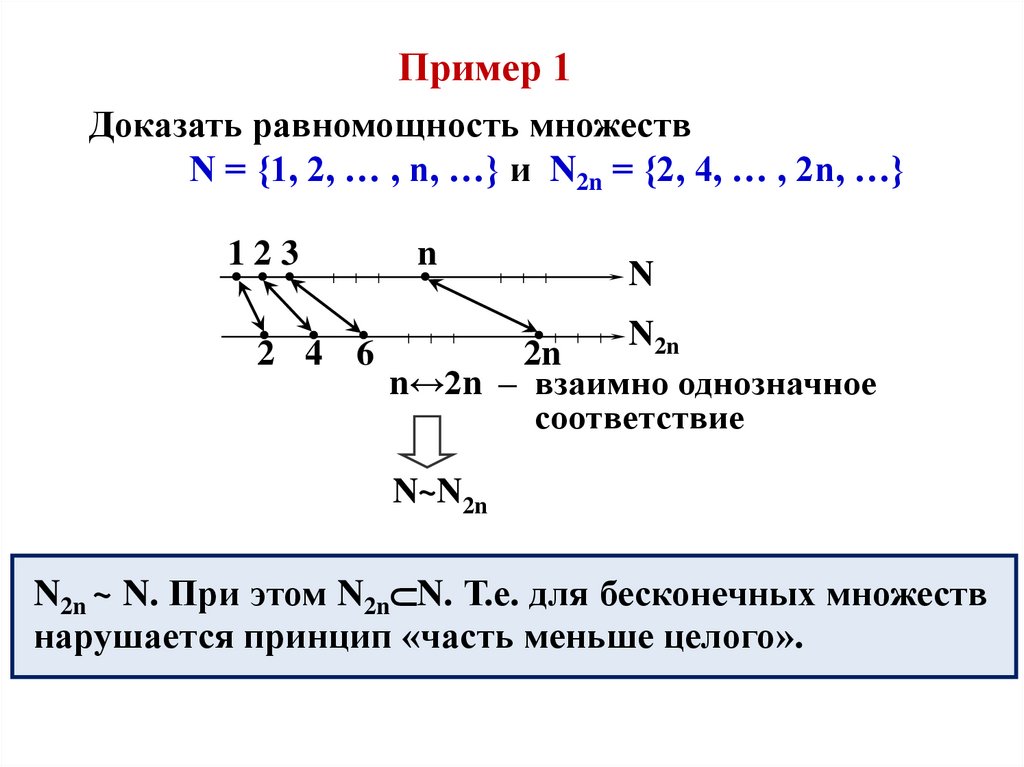
Пример 1
Доказать равномощность множеств
N = {1, 2, … , n, …} и N2n = {2, 4, … , 2n, …}
123
n
N
N2n
2 4 6
2n
n↔2n – взаимно однозначное
соответствие
N~N2n
N2n ~ N. При этом N2n N. Т.е. для бесконечных множеств
нарушается принцип «часть меньше целого».

17.

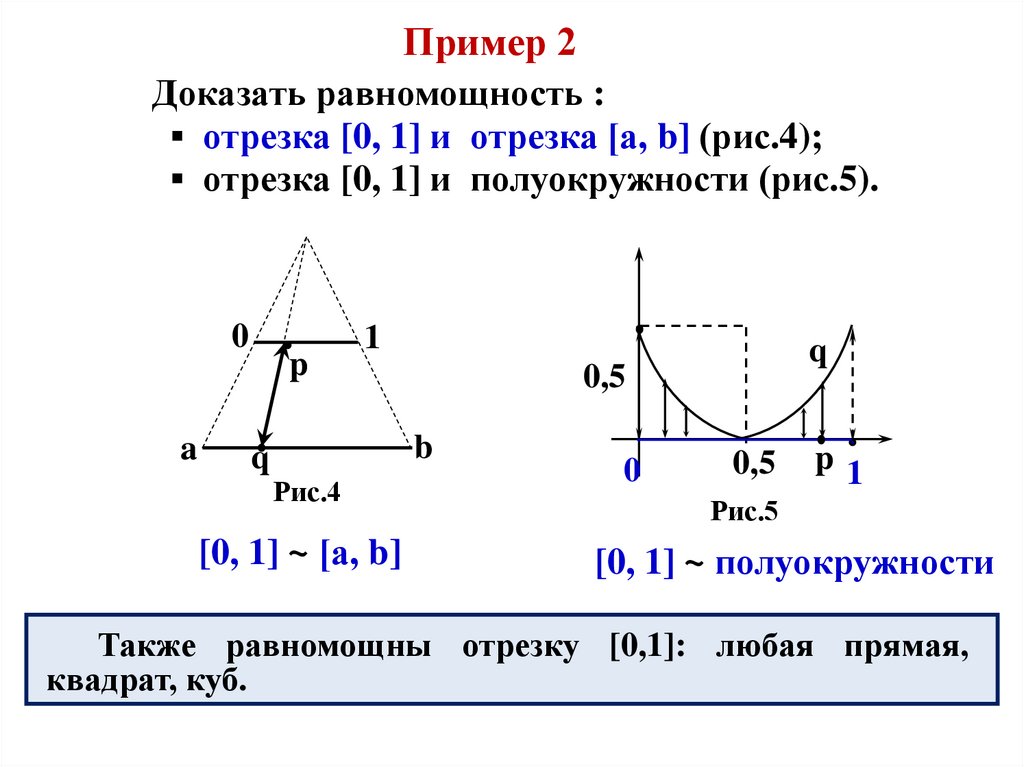
Пример 2
Доказать равномощность :
▪ отрезка [0, 1] и отрезка [а, b] (рис.4);
▪ отрезка [0, 1] и полуокружности (рис.5).
0
a
p
1
0,5
b
q
Рис.4
[0, 1] ~ [а, b]
q
0
0,5
p1
Рис.5
[0, 1] ~ полуокружности
Также равномощны отрезку [0,1]: любая прямая,
квадрат, куб.

18.

Выводы по второму вопросу
Множества А и В являются равномощными,
если между ними существует взаимно
однозначное отображение (соответствие).
Мощность конечного множества есть число его
элементов,
а
мощность
бесконечного
множества – это запас его элементов.
18

19.

3. СЧЕТНЫЕ, НЕСЧЕТНЫЕ
МНОЖЕСТВА,
ИХ СВОЙСТВА

20.

СЧЕТНЫЕ МНОЖЕСТВА
Счетными
называют
бесконечные
равномощные множеству натуральных чисел N.
▪
мн-ва,
В примере 1 доказано, что N~N2n , значит N2n – счетное.
▪ Все счетные мн-ва имеют мощность 0 (алеф-нуль)
множества N
Пример 3
Доказать счетность А=N\{1,2} = {3, 4, … , n, …}

21.

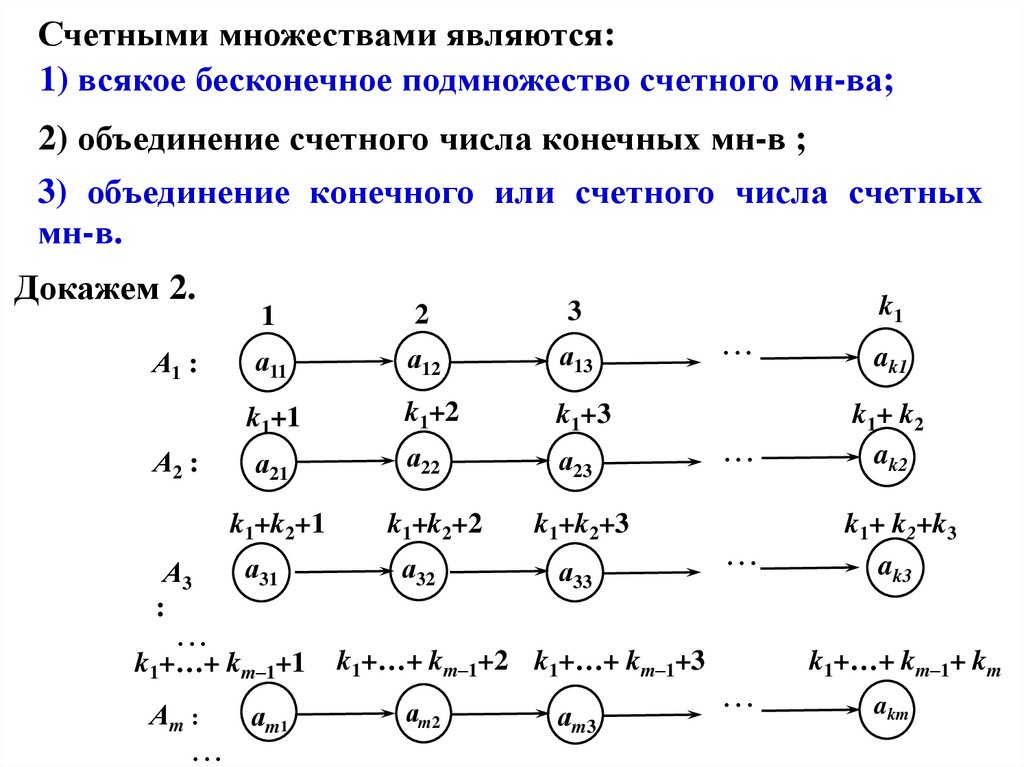
Счетными множествами являются:
1) всякое бесконечное подмножество счетного мн-ва;
2) объединение счетного числа конечных мн-в ;
3) объединение конечного или счетного числа счетных
мн-в.
Докажем 2.
А1 :
А2 :
А3
:
1
2
3
а11
а12
а13
k1+1
k1+2
k1+3
а21
а22
а23
k1+k2+1
k1+k2+2
k1+k2+3
а31
а32
а33
...
k1+…+ km–1+1
Аm :
...
аm 1
k1
...
...
...
k1+…+ km–1+2 k1+…+ km–1+3
аm2
аm3
ak1
k1+ k2
ak2
k1+ k2+k3
ak3
k1+…+ km–1+ km
...
akm

22.

НЕСЧЕТНЫЕ МНОЖЕСТВА
Несчетными называют бесконечные мн-ва, которые не
являются счетными, т.е. элементы которых невозможно
занумеровать всеми натуральными числами.
теорема Кантора:
Множество действительных чисел отрезке [0, 1] не счетно
Множество точек на отрезке [0, 1] несчетно
Пусть [0, 1] счетное
№ числа Число
1
0, а11 а12 а13 …
2
0, а21 а22 а23 …
3
0, а31 а32 а33 …
и т.д. где aij – конкретные цифры.
дроби 0, b1 b2 b3….,
где b1 ≠ a11, b2 ≠ a22,
b3 ≠ a33, … нет среди
занумерованных
противоречие
[0, 1] несчетно

23.

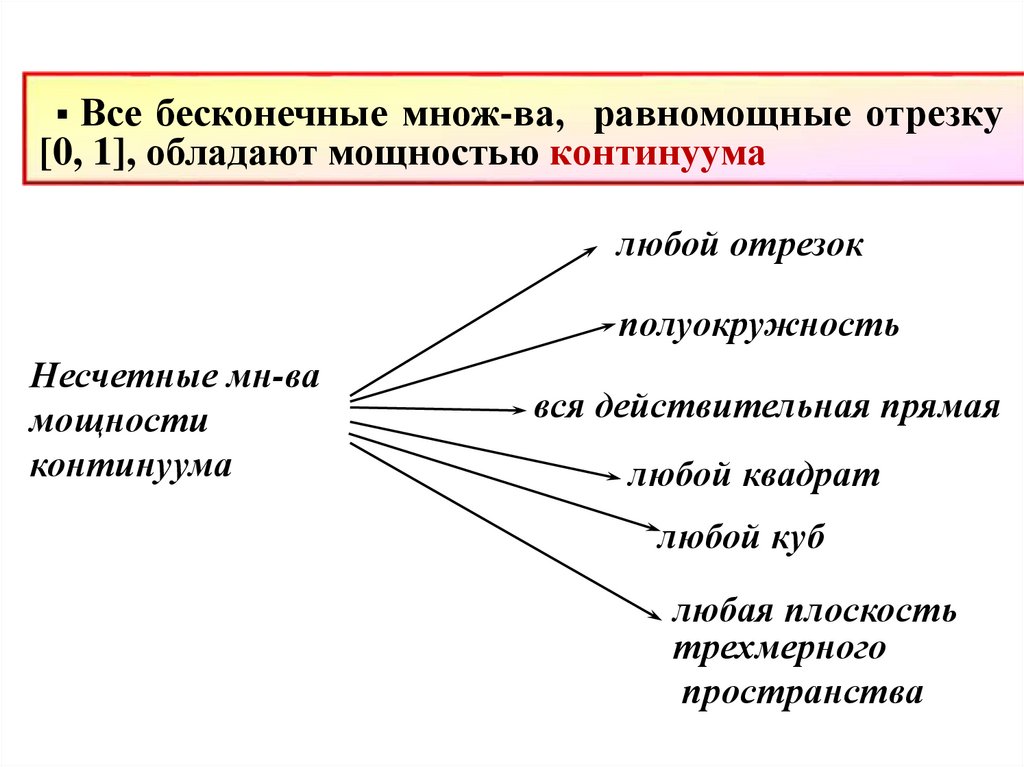
▪ Все бесконечные множ-ва, равномощные отрезку
[0, 1], обладают мощностью континуума
любой отрезок
полуокружность
Несчетные мн-ва
мощности
континуума
вся действительная прямая
любой квадрат
любой куб
любая плоскость
трехмерного
пространства

24.

Выводы по третьему вопросу
Бесконечные
множества,
равномощные
множеству натуральных чисел, являются
счетными. Среди бесконечных множеств они
обладают наименьшей мощностью (мощность
алеф-нуль).
Бесконечные множества, которые не являются
счетными, называют несчетными. Несчетные
множества, равномощные множеству точек
отрезка [0, 1], обладают мощностью
континуума.
24

25.

4. ФУНКЦИЯ
КАК ОТОБРАЖЕНИЕ

26.

■
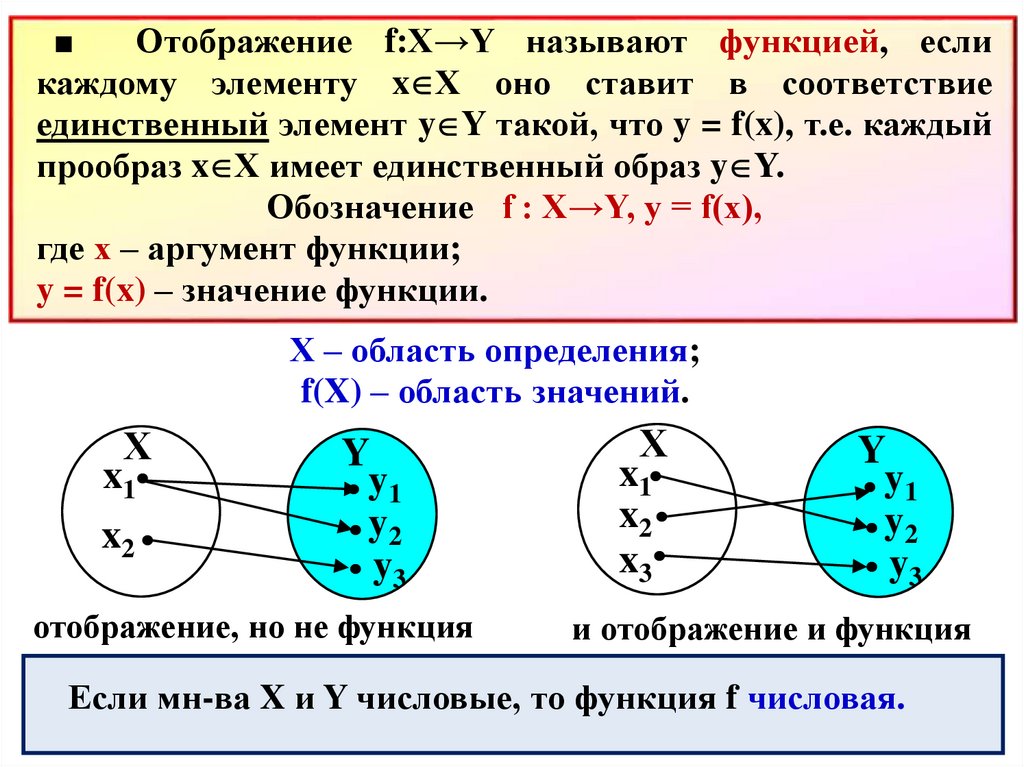
Отображение f:X→Y называют функцией, если
каждому элементу x Х оно ставит в соответствие
единственный элемент y Y такой, что y = f(x), т.е. каждый
прообраз x Х имеет единственный образ y Y.
Обозначение f : X→Y, y = f(x),
где х – аргумент функции;
y = f(x) – значение функции.
Х – область определения;
f(X) – область значений.
Х
x1
x2
Y
y1
y2
y3
отображение, но не функция
Х
x1
x2
x3
Y
y1
y2
y3
и отображение и функция
Если мн-ва X и Y числовые, то функция f числовая.

27.

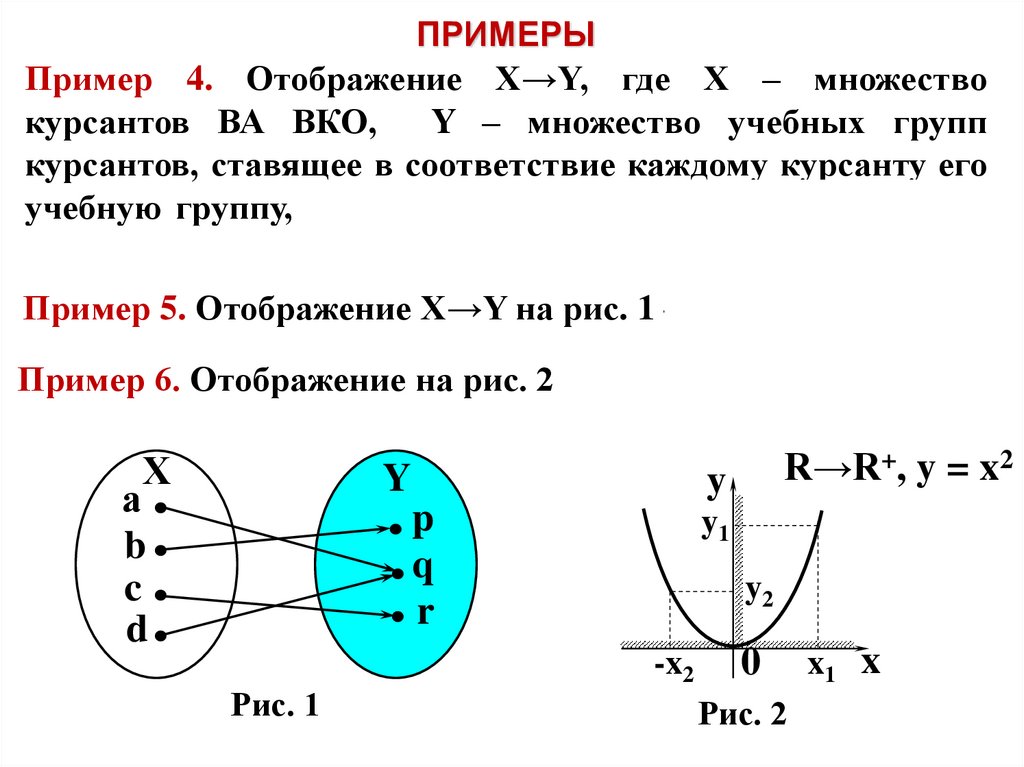
ПРИМЕРЫ
Пример 4. Отображение Х→Y, где Х – множество
курсантов ВА ВКО,
Y – множество учебных групп
курсантов, ставящее в соответствие каждому курсанту его
учебную группу, является функцией, т.к. каждый курсант
числится ровно в одной учебной группе.
Пример 5. Отображение X→Y на рис. 1 – функция.
Пример 6. Отображение на рис. 2 – функция
Х
Y
а
b
c
d
y
p
q
r
Рис. 1
R→R+, y = x2
y1
y2
-x2
0
Рис. 2
x1 x

28.

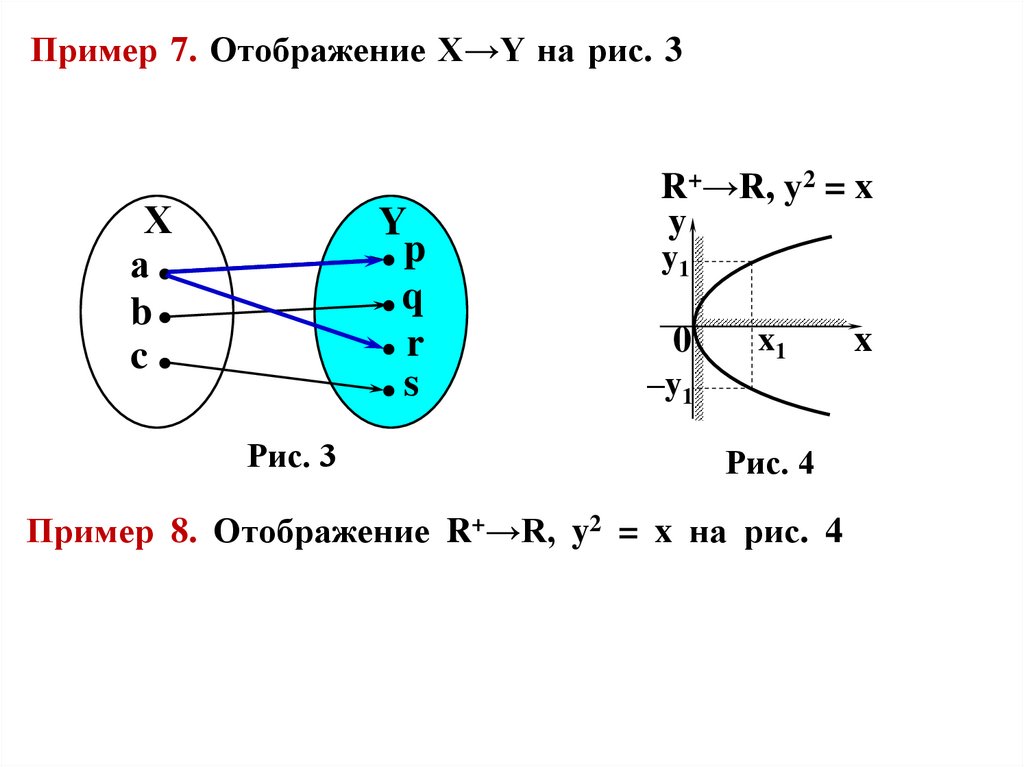
Пример 7. Отображение X→Y на рис. 3 – не функция, т.к.
прообразу а Х соответствует не один, а два образа р, r Y.
Х
а
b
c
Y
p
q
r
s
Рис. 3
R+→R, y2 = x
y
y1
0
x1
x
–y1
Рис. 4
Пример 8. Отображение R+→R, y2 = x на рис. 4 тоже не
является функцией, т.к. каждый прообраз х1 R+ имеет два
разных образа у R (y1 и –y1 ).

29.

ВИДЫ ФУНКЦИЙ
■ Функция f : Х→Y, y = f(x) называется инъективной, если
для любых х1, x2 Х из равенства f(x1) = f(x2) следует х1 = х2,
т.е. если х1 х2, то f(x1) f(x2) – разным значениям
аргумента соответствуют разные значения функции.
■ Функция f : Х→Y, y = f(x) называется сюръективной,
если для каждого y Y существует х Х такой, что y = f(x),
т.е. каждый y имеет прообраз х.
■ Функция f называется биективной,
одновременно инъективная и сюръективная.
если
Т.о. отображение f является биективной ф-цией, если
1) каждый х Х имеет единственный образ y Y,
2) разным х Х соответствуют разные y Y,
3) каждый y Y имеет прообраз х Х,
Биекция = взаимно однозначное отображение.
она

30.

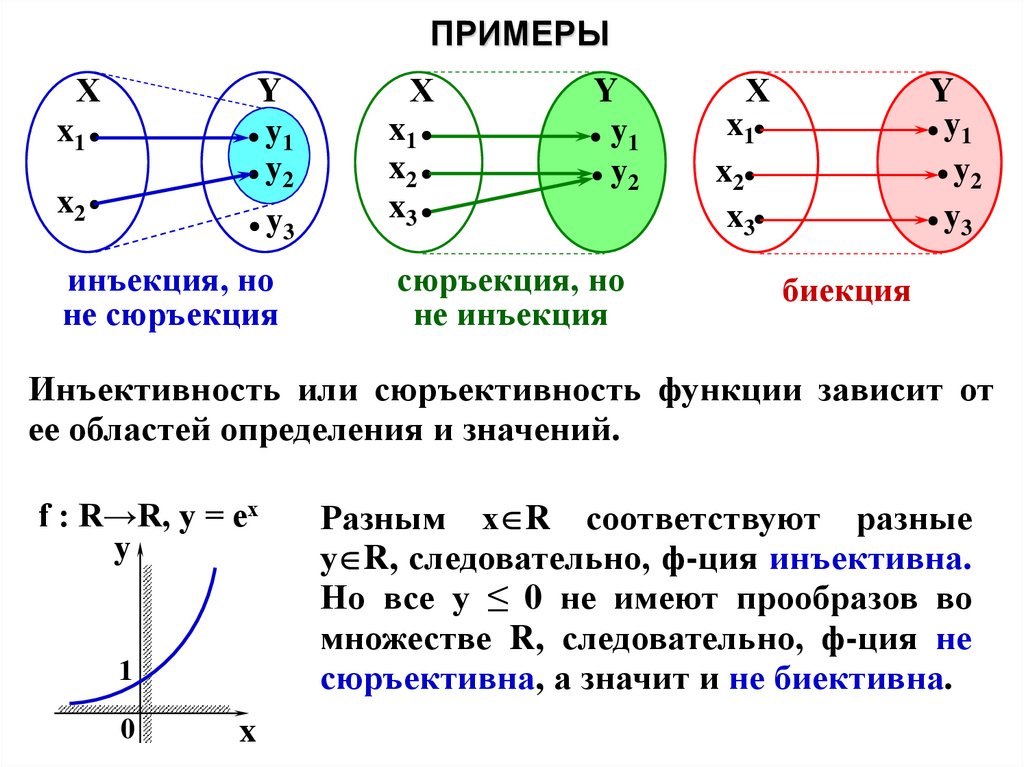
ПРИМЕРЫ
Х
Y
y1
y2
x1
x2
y3
инъекция, но
не сюръекция
Х
x1
x2
x3
Y
y1
y2
сюръекция, но
не инъекция
Х
Y
y1
y2
y3
x1
x2
x3
биекция
Инъективность или сюръективность функции зависит от
ее областей определения и значений.
f : R→R, y = ех
y
1
0
x
Разным х R соответствуют разные
у R, следовательно, ф-ция инъективна.
Но все у ≤ 0 не имеют прообразов во
множестве R, следовательно, ф-ция не
сюръективна, а значит и не биективна.

31.

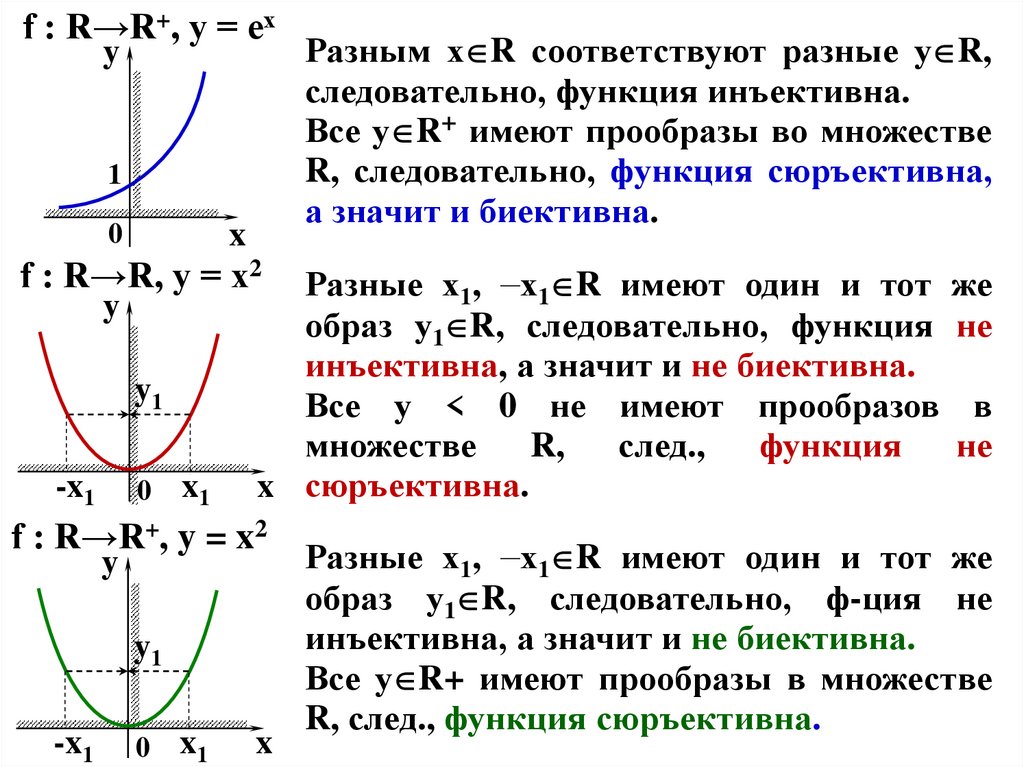
f : R→R+, y = ех
y
1
x
0
Разным х R соответствуют разные у R,
следовательно, функция инъективна.
Все у R+ имеют прообразы во множестве
R, следовательно, функция сюръективна,
а значит и биективна.
f : R→R, y = x2
y
y1
-x1
0
x1
Разные х1, –х1 R имеют один и тот же
образ у1 R, следовательно, функция не
инъективна, а значит и не биективна.
Все у < 0 не имеют прообразов в
множестве
R,
след.,
функция не
x сюръективна.
f : R→R+, y = x2
y
y1
-x1
0
x1
x
Разные х1, –х1 R имеют один и тот же
образ у1 R, следовательно, ф-ция не
инъективна, а значит и не биективна.
Все у R+ имеют прообразы в множестве
R, след., функция сюръективна.

32.

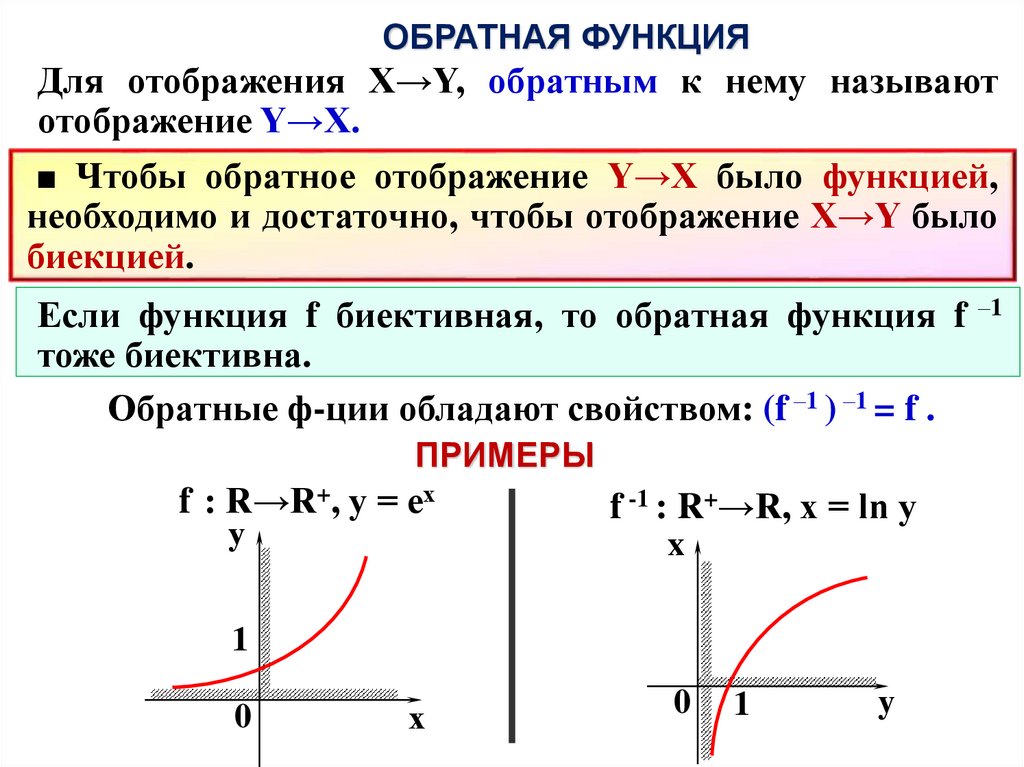
ОБРАТНАЯ ФУНКЦИЯ
Для отображения Х→Y, обратным к нему называют
отображение Y→Х.
■ Чтобы обратное отображение Y→Х было функцией,
необходимо и достаточно, чтобы отображение Х→Y было
биекцией.
Если функция f биективная, то обратная функция f –1
тоже биективна.
Обратные ф-ции обладают свойством: (f –1 ) –1 = f .
ПРИМЕРЫ
f : R→R+, у = ех
у
f -1 : R+→R, x = ln y
x
1
0
х
0
1
y

33.

КОМПОЗИЦИЯ ФУНКЦИЙ
Композицией функций f : X→Z, z = f(x) и g : Z→Y, y = g(z),
называется ф-ция g○f : X→Y, y = g(f(x)), осуществляющая
сначала отображение X→Z, а затем Z→Y, т.е. в итоге X→Y.
g○f
х
y
z = f(x) у = g( z ) g○f = g(f(x))
g
f
z
ПРИМЕР
Даны функции f : R→ R+, f(x) = 1 + x2 и g : R+→ R,
g(x) = ln x. Найти композицию g○f.
f = 1 + x2
y = ln x
g○f =g(f(x))= ln (1 + x2)
f○g =f(g(x))= 1 + (ln x)2

34.

Композиция двух биективных функций тоже биективная
функция.
Обратное не верно:
если g○f – биективная, то f
инъективная, а g сюръективная.
Свойства композиции: 1) (g○f) –1 = g –1 ○f –1; 2) g○f ≠ f○g .
Если f : Х→Y – биективная функция, то существует
обратная ей функция f –1 : Y→Х , и с помощью
композиции f и f –1 можно отображать множество Х или
Y само на себя:
f –1○f : X→X
и f○f –1: Y→Y

35.

Выводы по четвертому вопросу
Если функция является биективной, то
существует обратная ей функция, которая
тоже биективна.
Композиция двух функций представляет собой
новую функцию, осуществляющую сначала
отображение множеств первой функции, а
затем, с его учетом, отображение множеств
второй функции.
35

36.

1. ИЗУЧИТЬ: литературу л. 1/о с. 22-37, л.1/д с. 30-34,
л.2/о м.1.1.4-1.1.7(Э).
2. ОТРАБОТАТЬ:
конспект
лекции.
Основное
внимание обратить на понятия отображения
множеств, равномощных множеств, счетных и
несчетных множеств, а также инъективной,
сюръективной, биективной и обратной функции.
3. БЫТЬ ГОТОВЫМ: к практическому занятию № 9
«Решение задач на анализ функций и исследование
множеств на счетность, несчетность».