Ассиметричные криптосистемы

1.

Ассиметричные криптосистемы

2. Симметричные криптоалгоритмы

Минусы:
1) для каждой пары, переписывающейся между
собой, необходимо создавать свой секретный
симметричный ключ
2) в системе из N пользователей количество ключей
N2/2
3) при нарушении конфиденциальности какой-либо
рабочей станции злоумышленник получает
доступ ко всем ключам этого пользователя и
может отправлять сообщения всем абонентам, с
которыми "жертва" вела переписку

3. Асимметричная криптография

Появилась 20лет назад
Изначально задумана как средство передачи
сообщений от одного объекта к другому
"отправитель" – лицо, шифрующее, а затем
отправляющее информацию по
незащищенному каналу
"получатель" – лицо, принимающее и
восстанавливающее информацию в ее исходном
виде

4. Процедура шифрования

Необратима даже по известному ключу
шифрования
Зная ключ шифрования и зашифрованный
текст, невозможно восстановить исходное
сообщение
Прочесть зашифрованное сообщение можно
только с помощью второго ключа – ключа
дешифрования

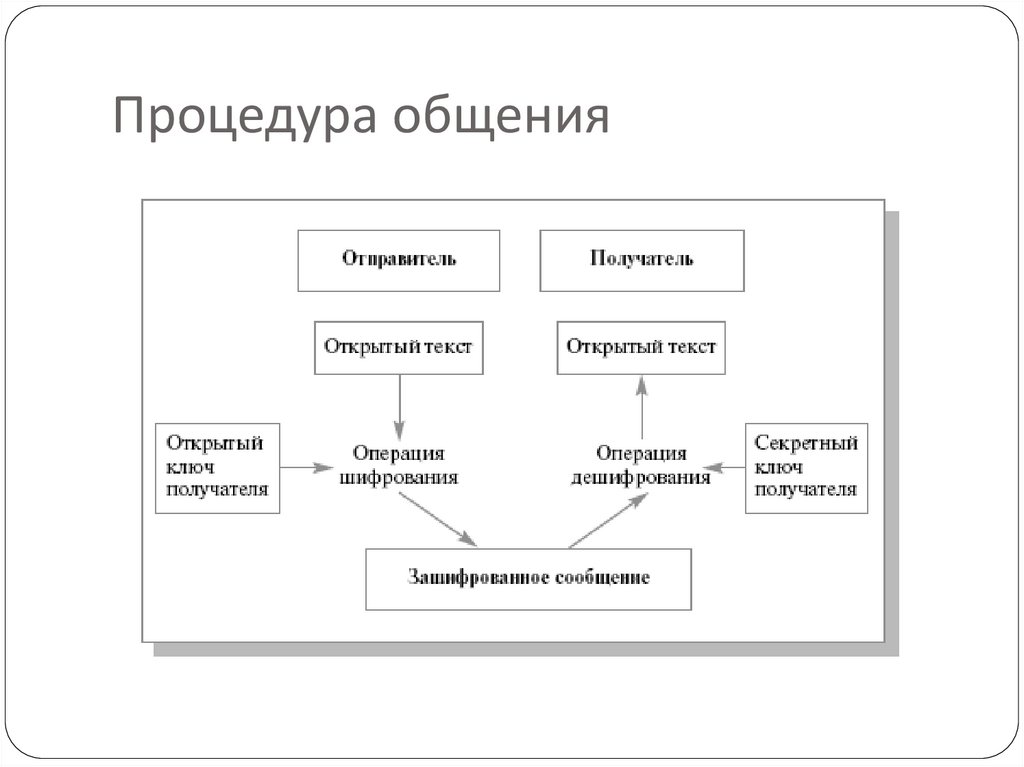
5. Основная идея

Для шифрования сообщения используется один
ключ – открытый (ключ шифрования)
При дешифровании используется другой ключ –
закрытый (ключ дешифрования, который известен
только получателю)

6. Процедура общения

7. Преимущества

В асимметричных системах количество
существующих ключей связано с количеством
абонентов линейно (в системе из N
пользователей используются 2*N ключей)
при нарушении конфиденциальности k-ой
рабочей станции злоумышленник узнает
только закрытый ключ: это позволяет ему
читать все сообщения, приходящие абоненту k,
но не позволяет выдавать себя за него при
отправке писем

8. Криптосистемы с ключом

С закрытым ключом – симметричные
криптосистемы . Проблема: передача ключа
С открытым ключом – ассиметричные
криптосистемы . Нет проблем передачи ключа
шифрования

9. Однонаправленные функции

Вся концепция криптосистем с открытым ключом
основана на применении однонаправленных
функций (one way functions). Неформально
однонаправленную функцию можно определить
следующим образом.
Пусть X и Y - произвольные множества.
Функция f(X) -> Y,
является однонаправленной, если для всех х,
входящих в Х, легко вычислить функцию f(x), и в то
же время для большинства y, входящих в Y,
получить любое значение x, входящее в X, такое что
f(x) = y достаточно сложно (при этом полагают, что
существует, по крайней мере, одно такое значение
x).

10. Алгоритм RSA

Предложен тремя исследователями-
математиками Рональдом Ривестом (R.Rivest) ,
Ади Шамиром (A.Shamir) и Леонардом
Адльманом (L.Adleman) в 1977-78 годах.

11. Этапы создания ключей

Выберем два очень больших простых числа p и q.
Определим n как результат умножения p на q
(n=p*q).
Выберем большое случайное число, которое
назовем d. Это число должно быть взаимно простым
с результатом умножения (p-1)*(q-1).
Определим такое число е, для которого является
истинным следующее соотношение: (e*d) mod ((p1)*(q-1)) = 1.
Назовем открытым ключом числа е и n, а
секретным ключем числа d и n.

12. Процедура шифрования

Отправитель разбивает свое сообщение на
блоки, равные k=[log2(n)] бит, где квадратные
скобки обозначают взятие целой части от
дробного числа.
Для каждого такого числа (назовем его mi)
вычисляется выражение ci=((mi)e)mod n.
Блоки ci и есть зашифрованное сообщение.
Их можно спокойно передавать по открытому
каналу, поскольку операция возведения в
степень по модулю простого числа, является
необратимой математической задачей.

13. Дешифрация

чтобы прочесть сообщение ci=((mi)e)mod n
достаточно возвести его в степень d по модулю
m : mi = ((ci)d)mod n

14. Шаг первый. Подготовка ключей

Выберем р=3 и q=11.
Определим n=3*11=33.
Найдем (р-1)*(q-1)=20. Следовательно в
качестве d выберем любое число, которое
является взаимно простым с 20, например d=3.
Выберем число e. В качестве такого числа может
быть взято любое число, для которого
удовлетворяется соотношение (e*3) mod 20 = 1,
например 7.

15. Шаг второй. Подготовка текста

Представим шифруемое сообщение как
последовательность целых чисел в диапазоне
0...32.
Пусть буква A изображается числом 1, буква B числом 2, а буква C - числом 3.
Тогда сообщение «САВ» можно представить в
виде последовательности чисел 3 1 2.

16. Шаг третий. Шифрование

Зашифруем сообщение, используя ключ {7,33}:
C1=(3^7) mod 33 = 2187 mod 33 = 9,
C2=(1^7) mod 33 = 1 mod 33 = 1,
C3=(2^7) mod 33 = 128 mod 33 = 29.

17. Дешифрация

Попытаемся расшифровать сообщение {9,1,29},
полученное в результате зашифрования по
известному ключу на основе секретного ключа
{3,33}:
M1=(9^3) mod 33 = 729 mod 33 = 3,
M2=(1^3) mod 33 = 1 mod 33 = 1,
M3=(29^3) mod 33 = 24389 mod 33 = 2.

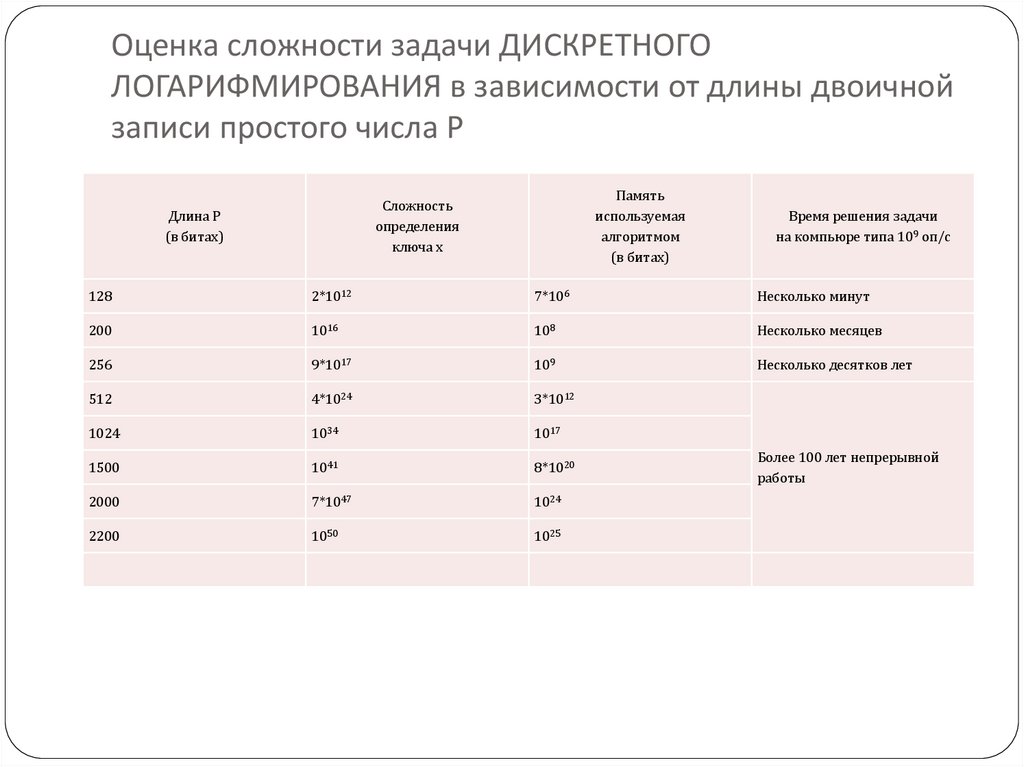
18. Оценка сложности задачи ДИСКРЕТНОГО ЛОГАРИФМИРОВАНИЯ в зависимости от длины двоичной записи простого числа P

Память
используемая
алгоритмом
(в битах)
Сложность
определения
ключа x
Длина P
(в битах)
Время решения задачи
на компьюре типа 109 оп/c
128
2*1012
7*106
Несколько минут
200
1016
108
Несколько месяцев
256
9*1017
109
Несколько десятков лет
512
4*1024
3*1012
1024
1034
1017
1500
1041
8*1020
2000
7*1047
1024
2200
1050
1025
Более 100 лет непрерывной
работы

19. Вывод

Криптографические системы с открытыми
ключами используют разные ключи.
Открытый и закрытый
Если средства шифрования разделены, то
секретность можно обеспечить без
засекречивания ключа шифрования, так как его
нельзя использовать для расшифровывания.

20. Задание

Зашифровать текст
«Грузите товар в серые мешки»

21. Задачи взаимодействия

вначале у А и В нет никакой общей секретной
информации, но в конце процедуры такая
общая секретная информация (общий ключ) у А
и В вырабатывается;
противник, который перехватывает все
передачи и знает, что хочет получить А и В, тем
не менее не может восстановить выработанный
общий ключ А и В.