Дискретная математика

1. Дискретная математика

«А математику уже затем учить следует,
что она ум в порядок приводит».
М.В. Ломоносов.

2. Литература:

Емеличев В.А. и др. Лекции по теории графов. М.: Наука,
1990.
Грэхем Р., Кнут Д. Конкретная математика. Основания
информатики – М.: Мир, 1998.
Эвнин А.Ю. Задачник по дискретной математике.
Издание второе, переработанное и дополненное.
Челябинск: Изд-во ЮУрГУ, 2002.
Эвнин А.Ю. Дискретная математика (конспект лекций)
Челябинск: Изд-во ЮУрГУ, 1998.
Комбинаторный анализ: задачи и упражнения / Под
общ. ред. К.А. Рыбникова. – М.: Наука, 1992.

3. Глава I. Элементы теории графов

«Теория без практики-мертва,
а практика без теории-слепа»
И. Кант

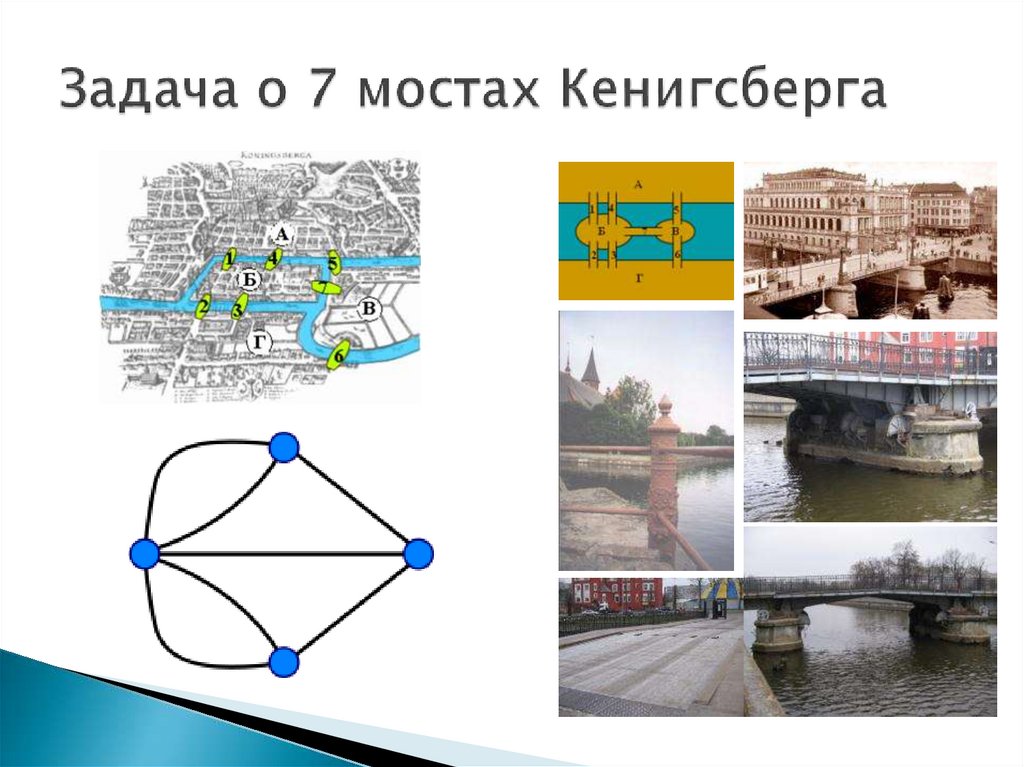
4. Задача о 7 мостах Кенигсберга

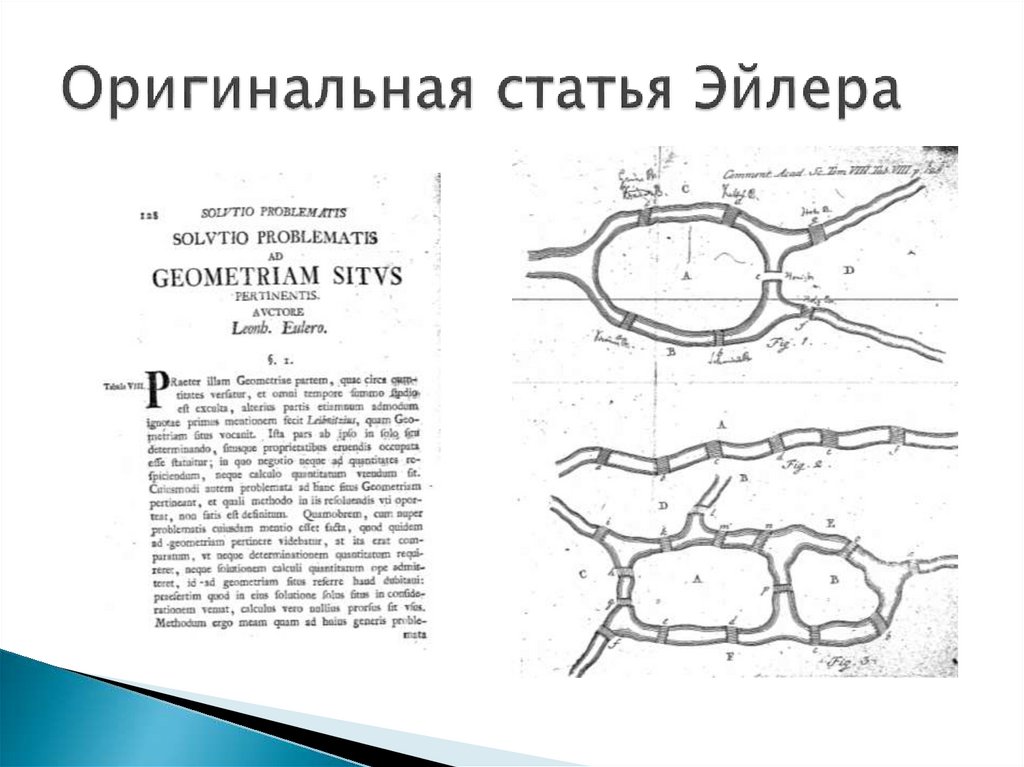
5. Оригинальная статья Эйлера

6. §1.1. Начальные понятия теории графов

1.
2.
3.
4.
5.
6.
7.
Основной целью является
рассмотрение вопросов:
Определение графа.
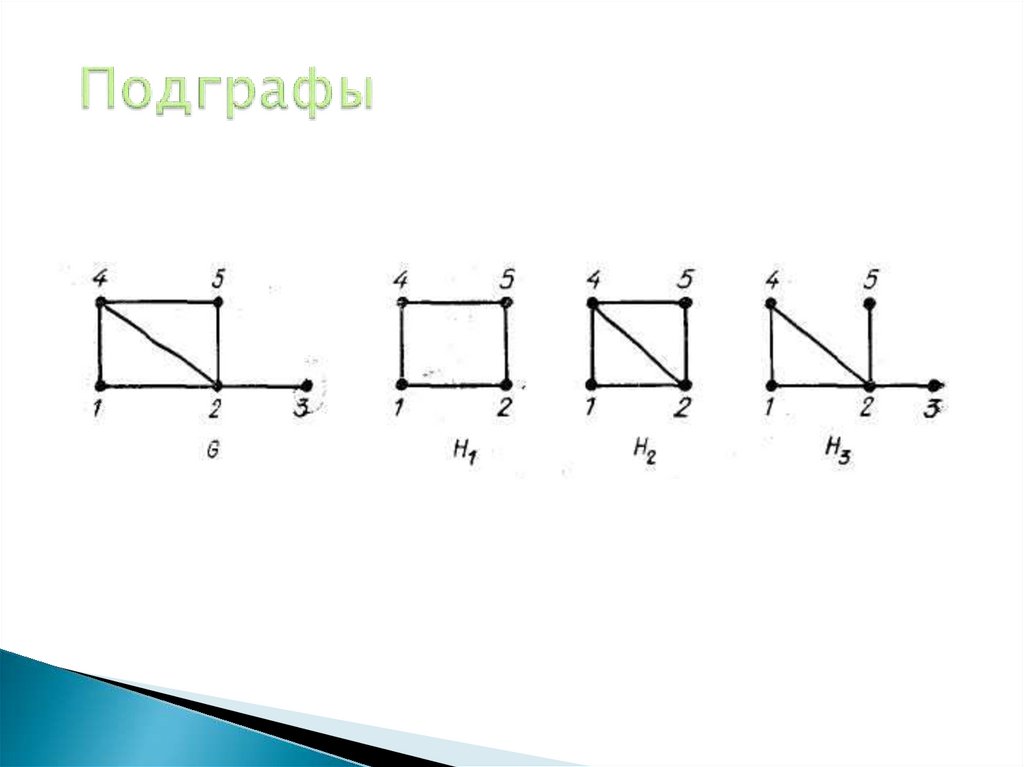
Подграфы.
Операции над графами .
Цепи, циклы, компоненты.
Степени вершин графа.
Матрицы, ассоциированные с графом.
Критерий двудольности графа.

7. ОПРЕДЕЛЕНИЕ ГРАФА

Определение. Пусть V – непустое множество,
Е — произвольное множество его
двухэлементных подмножеств. Пара (V,Е ),
где Е — произвольное подмножество
множества V (2), называется графом
(обыкновенным, неориентированным, или
простым графом).

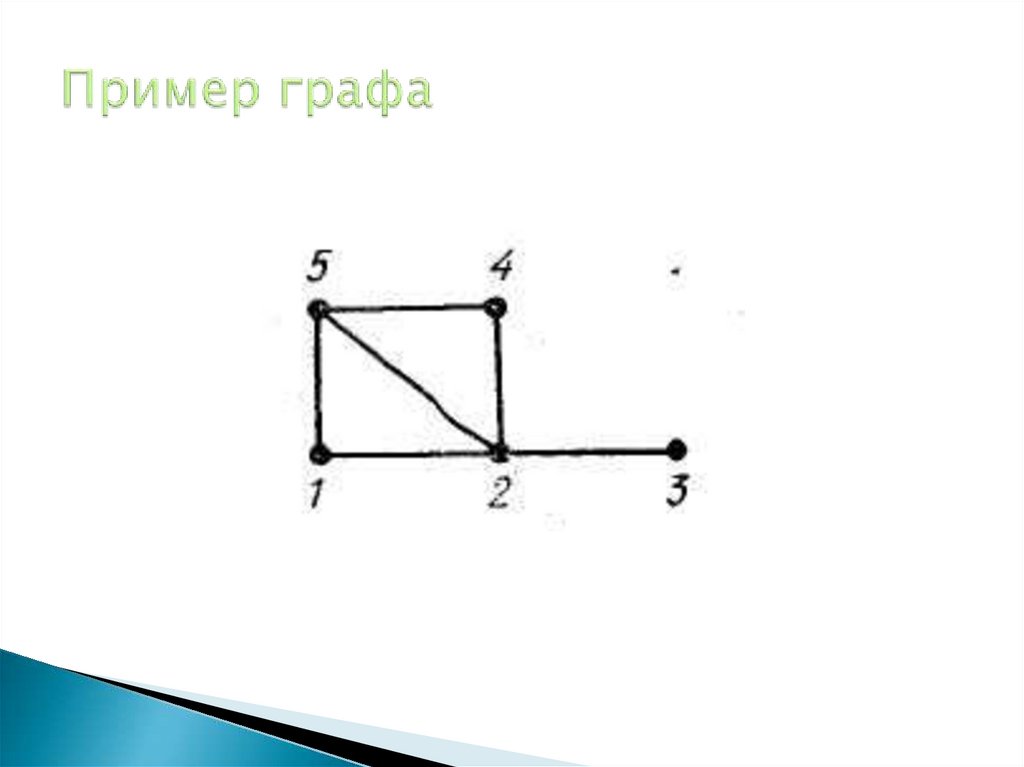
8. Пример графа

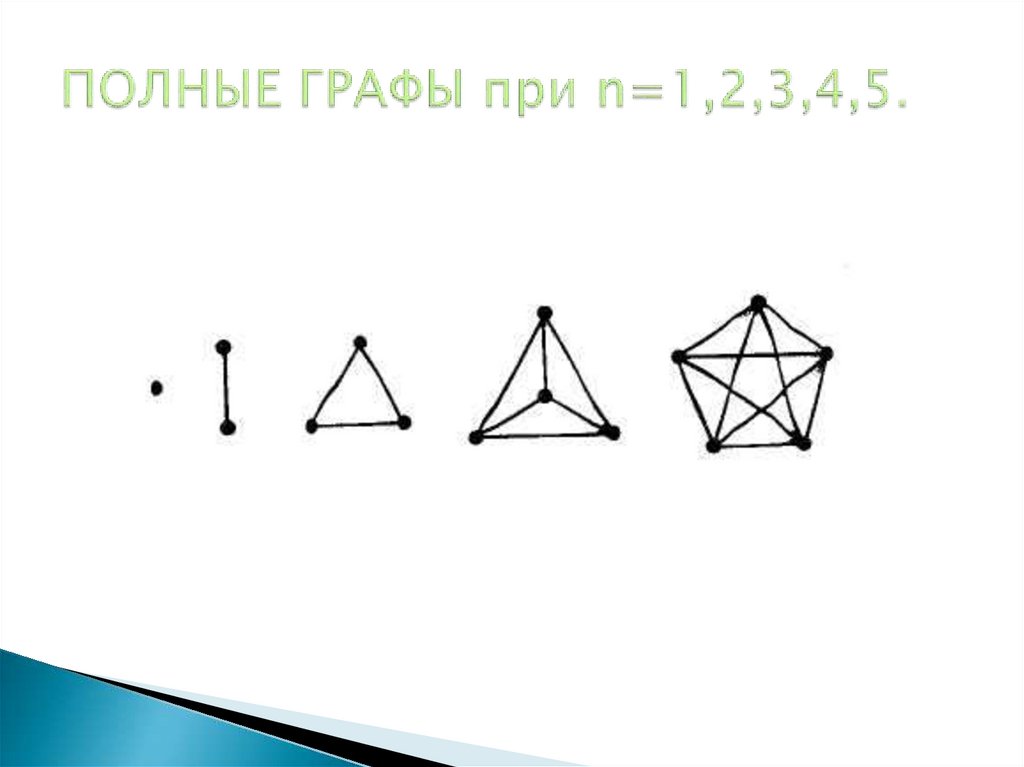
9. ПОЛНЫЕ ГРАФЫ при n=1,2,3,4,5.

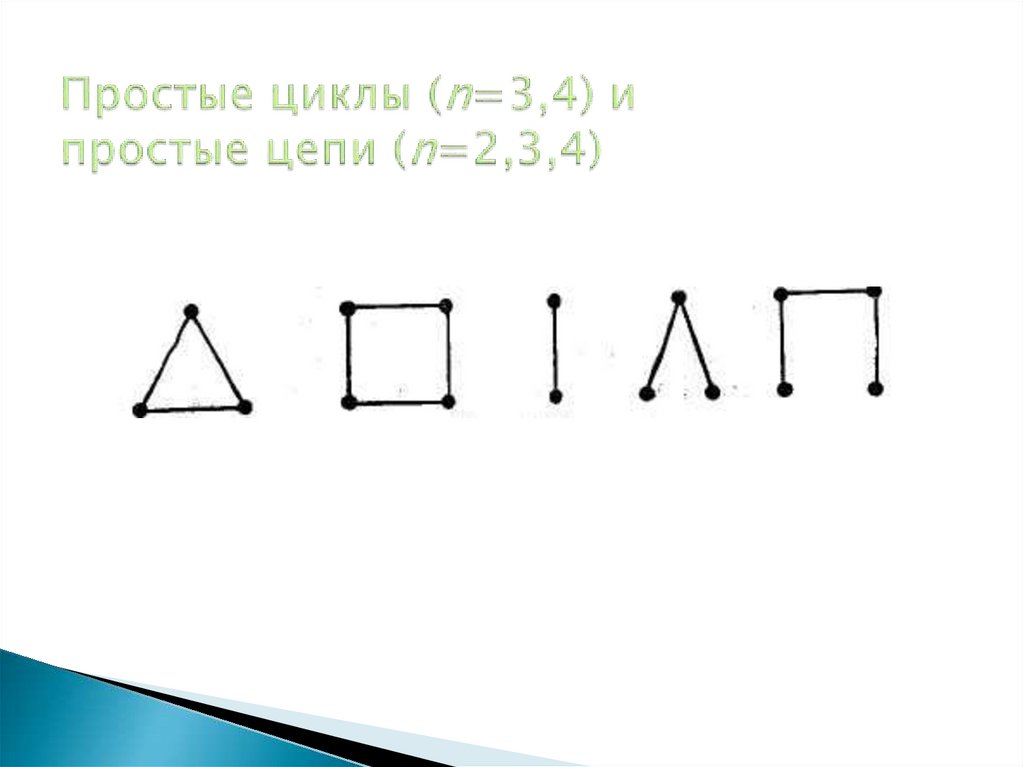
10. Простые циклы (n=3,4) и простые цепи (n=2,3,4)

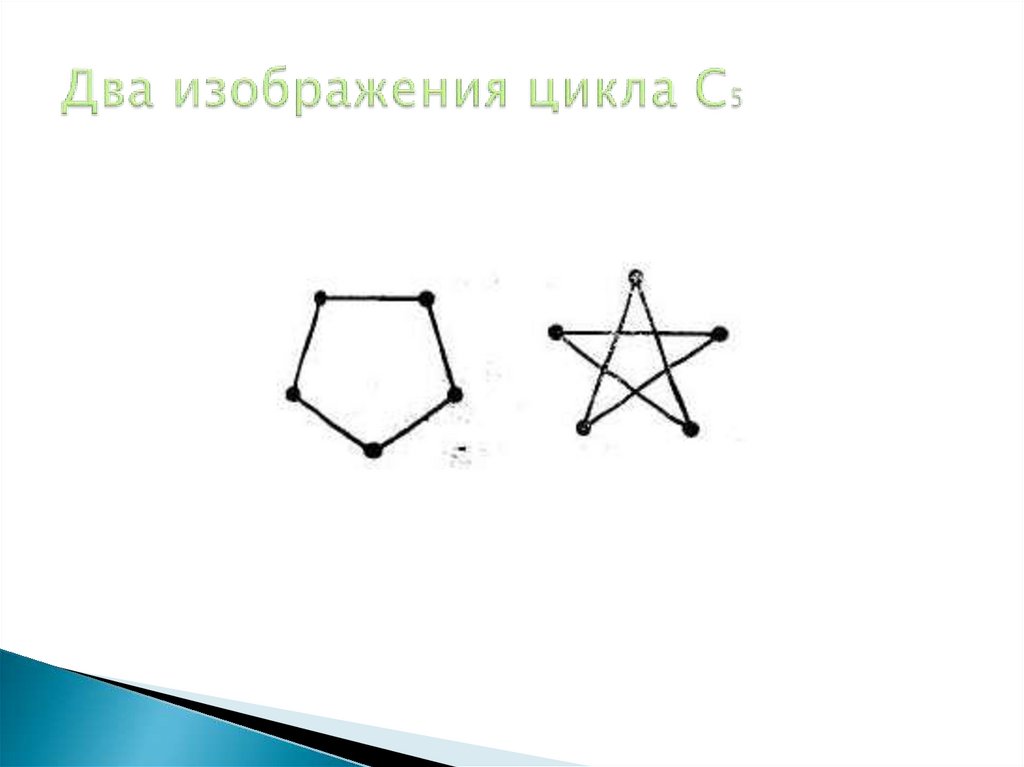
11. Два изображения цикла C5

12. КОЛЕСА Wn (n=3,4,5)

13. Граф Петерсена

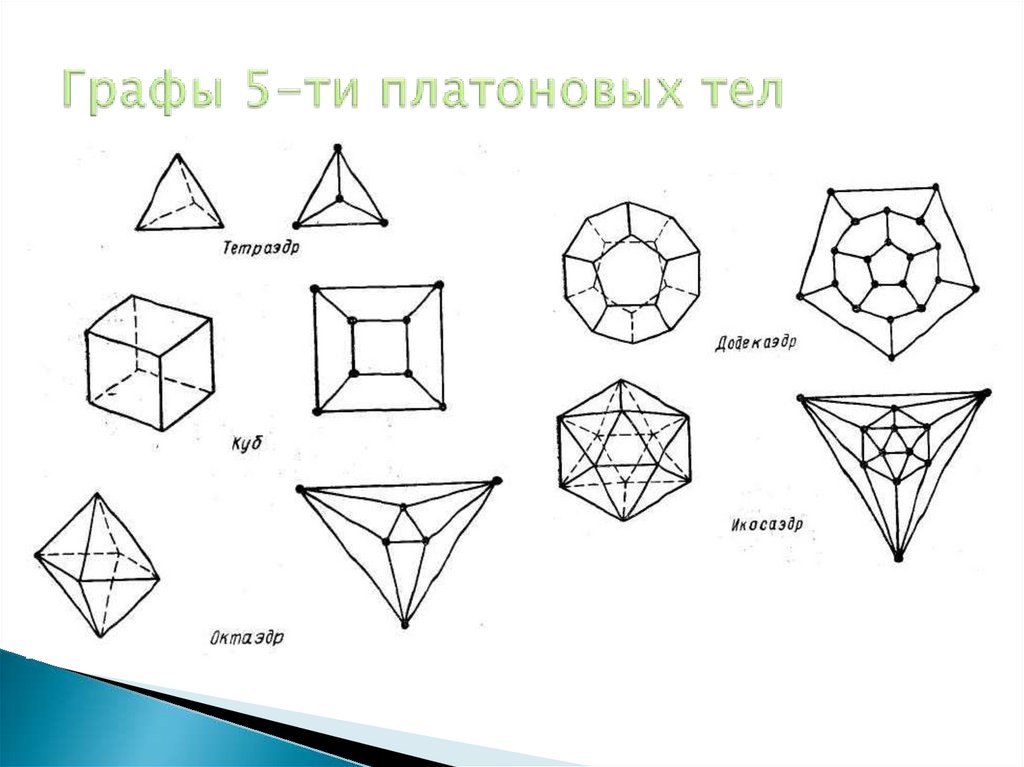
14. Графы 5-ти платоновых тел

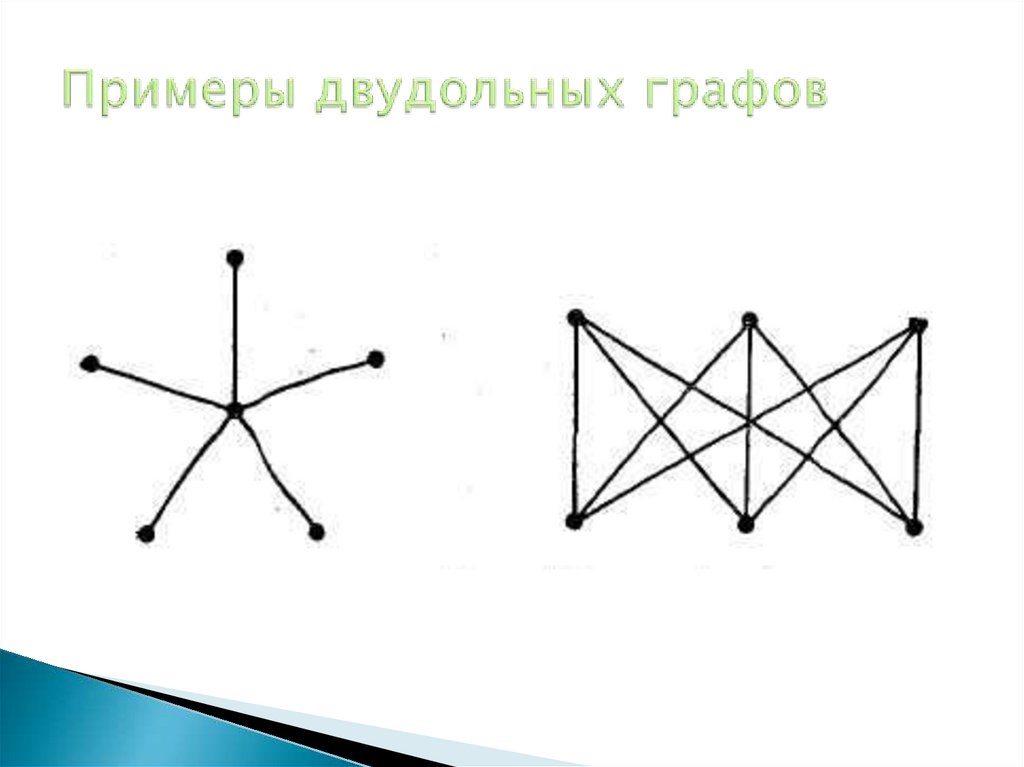
15. Примеры двудольных графов

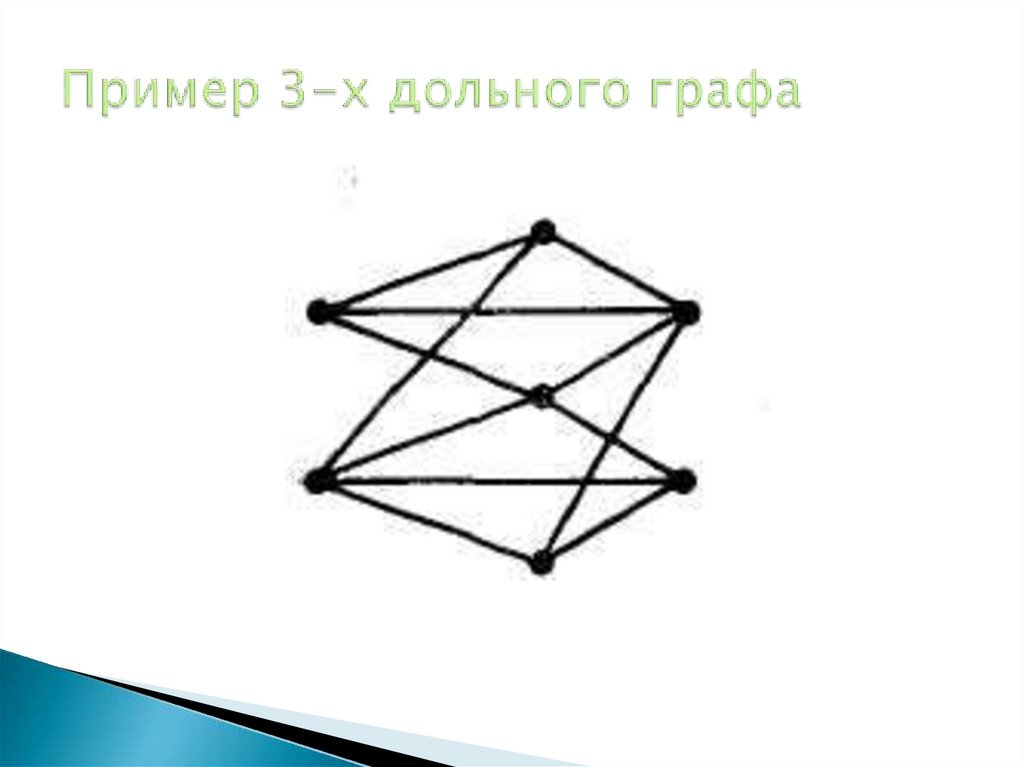
16. Пример 3-х дольного графа

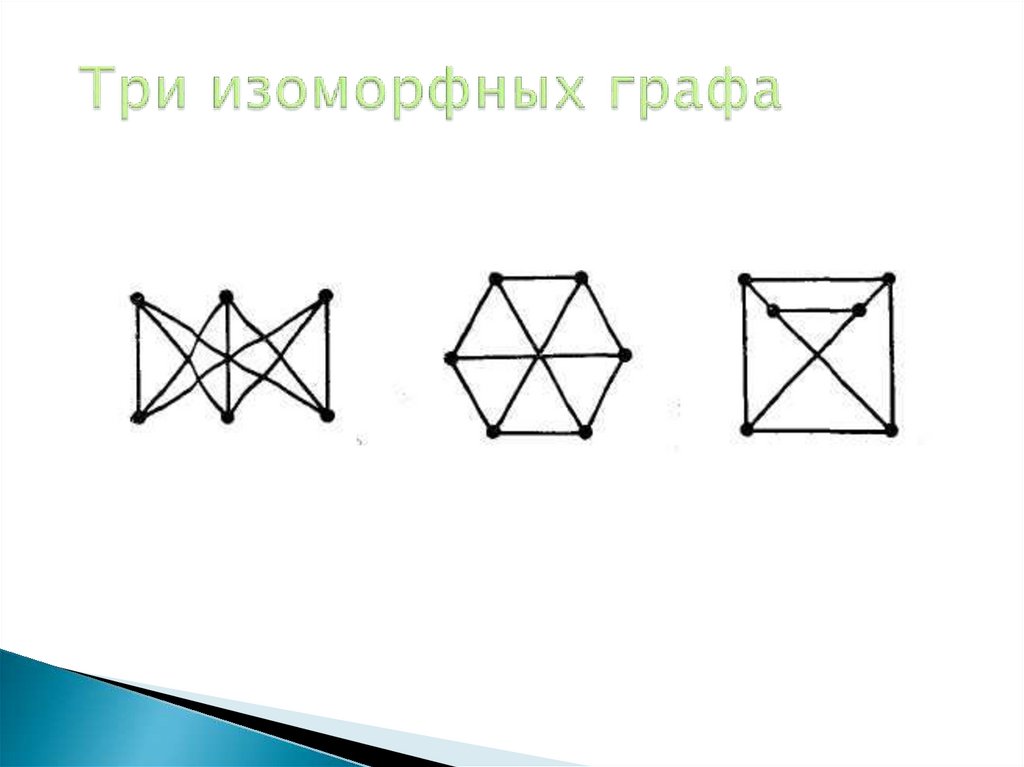
17. Три изоморфных графа

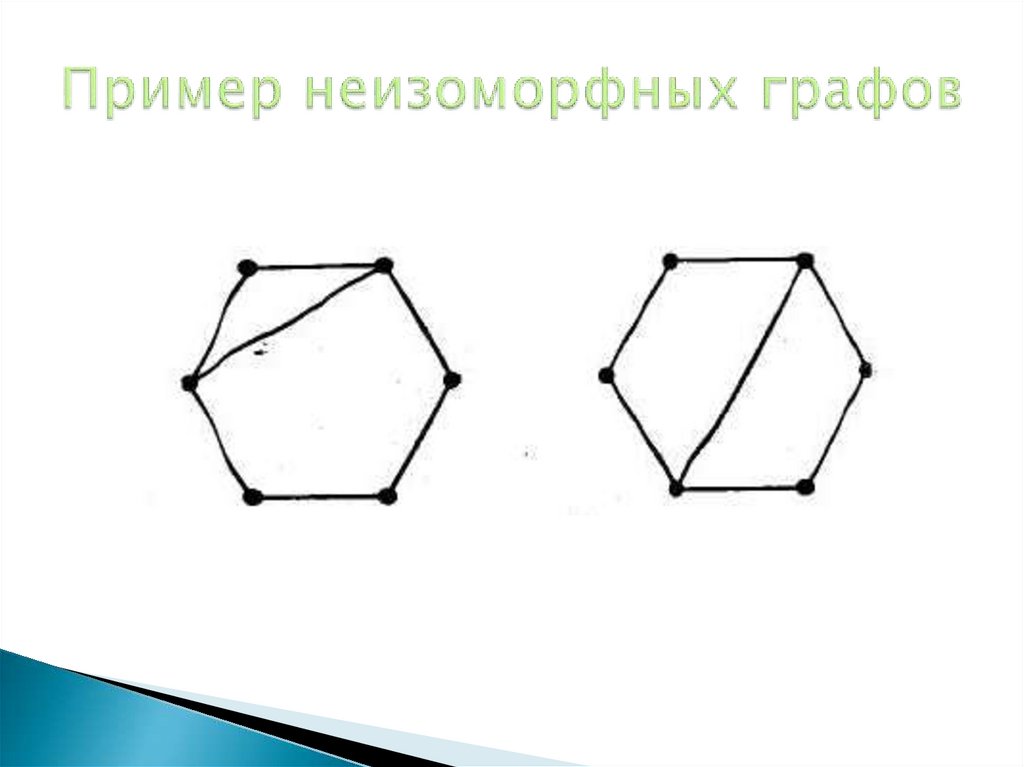
18. Пример неизоморфных графов

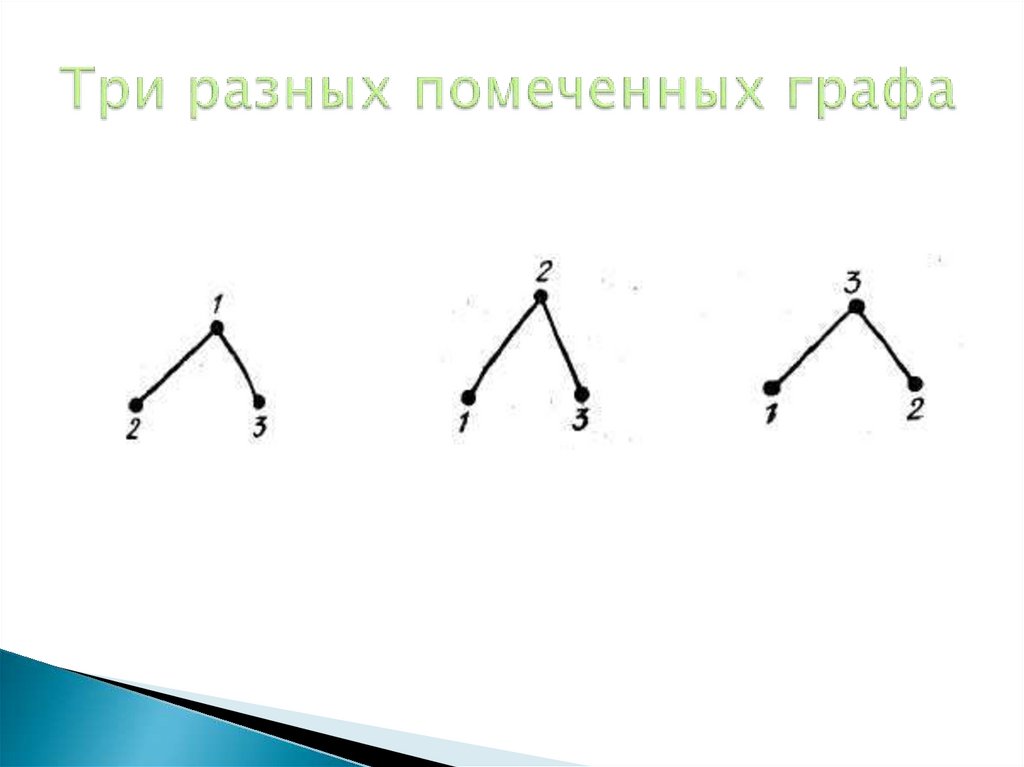
19. Три разных помеченных графа

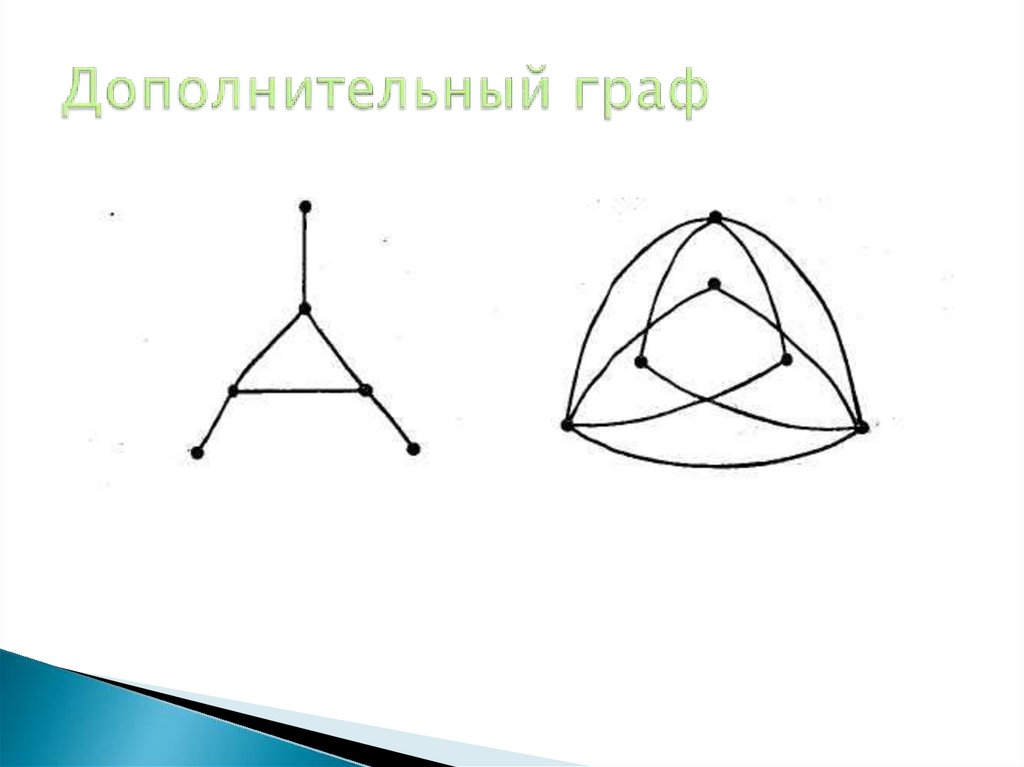
20. Дополнительный граф

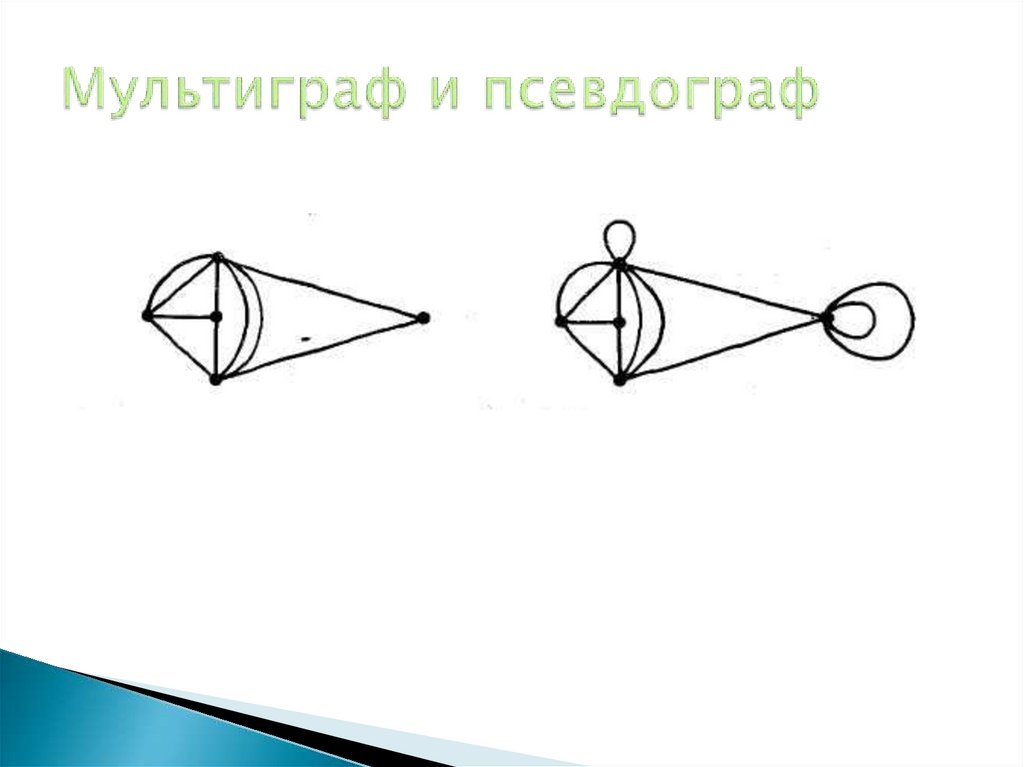
21. Мультиграф и псевдограф

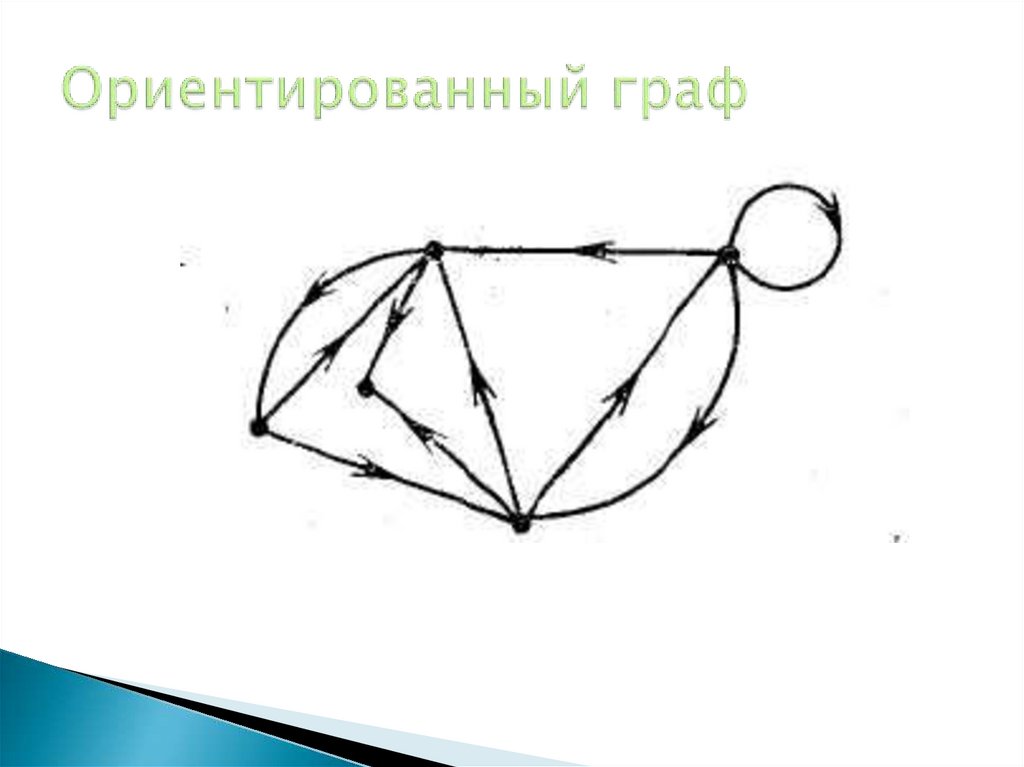
22. Ориентированный граф

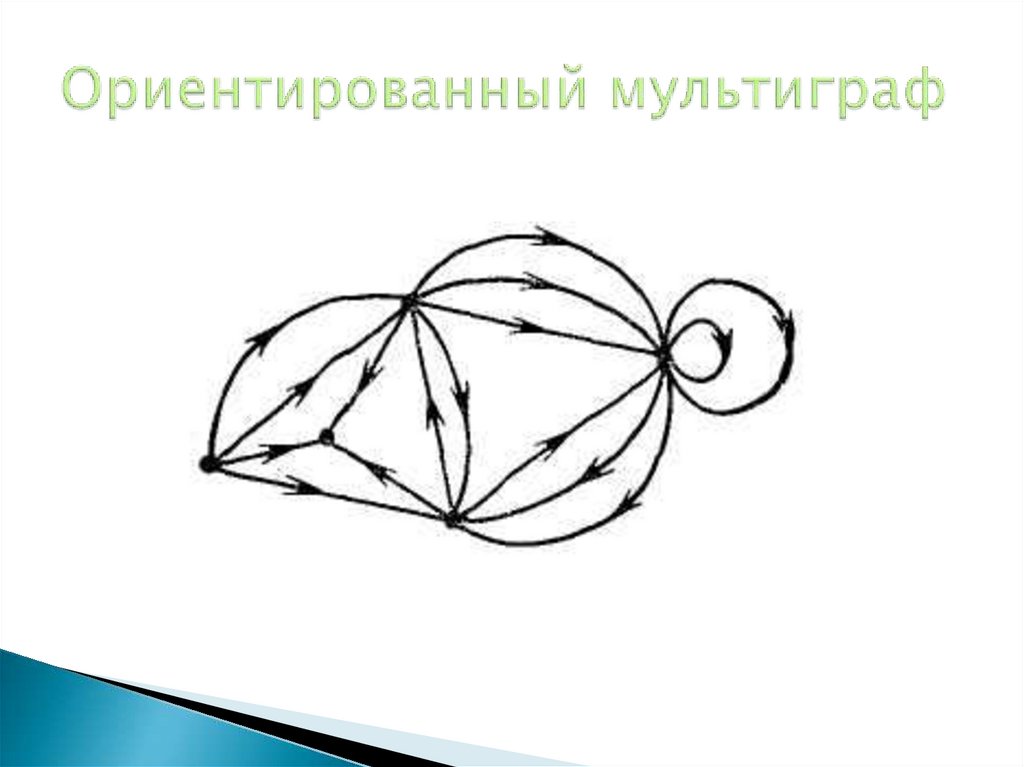
23. Ориентированный мультиграф

24. Подграфы

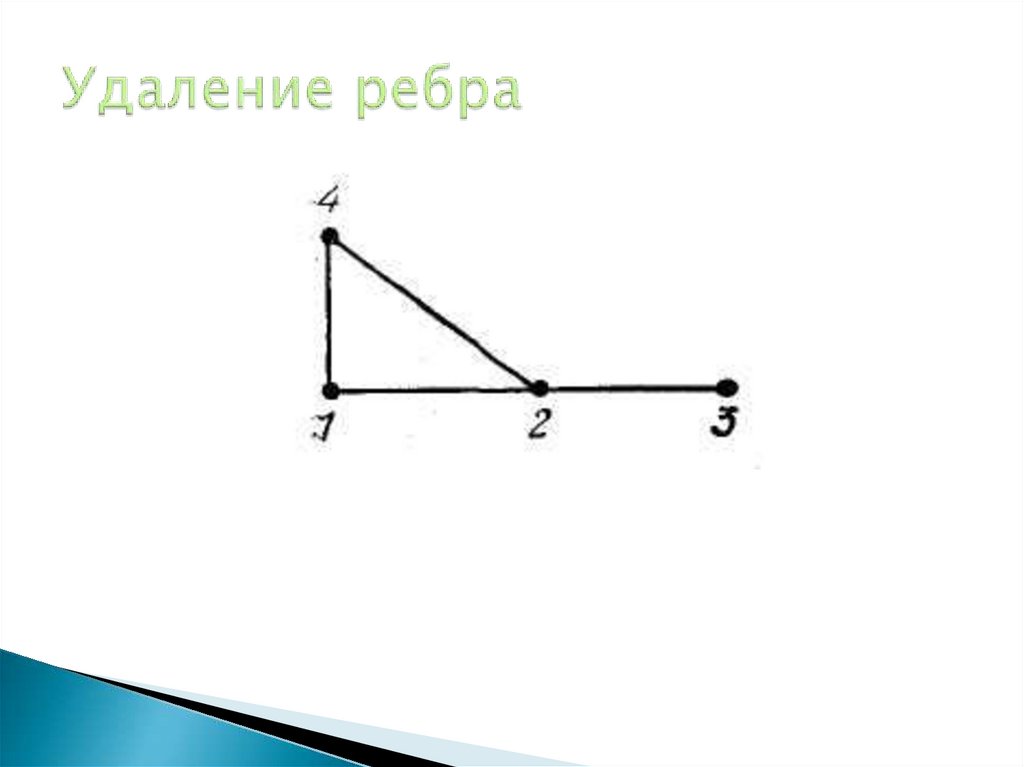
25. Удаление ребра

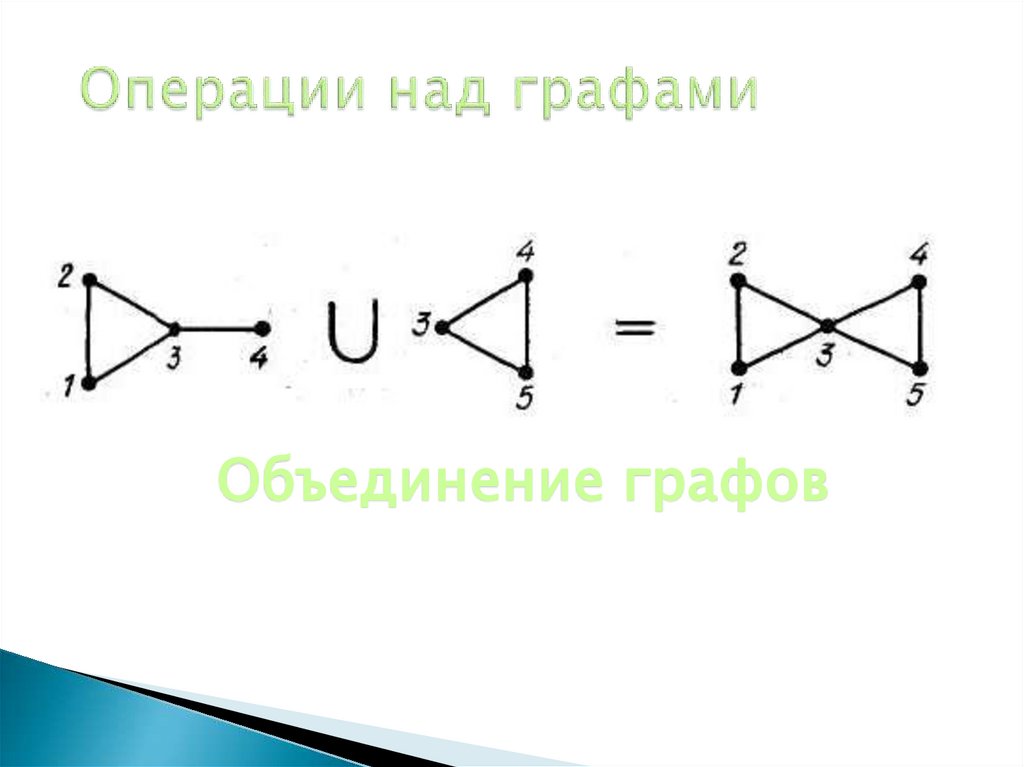
26. Операции над графами

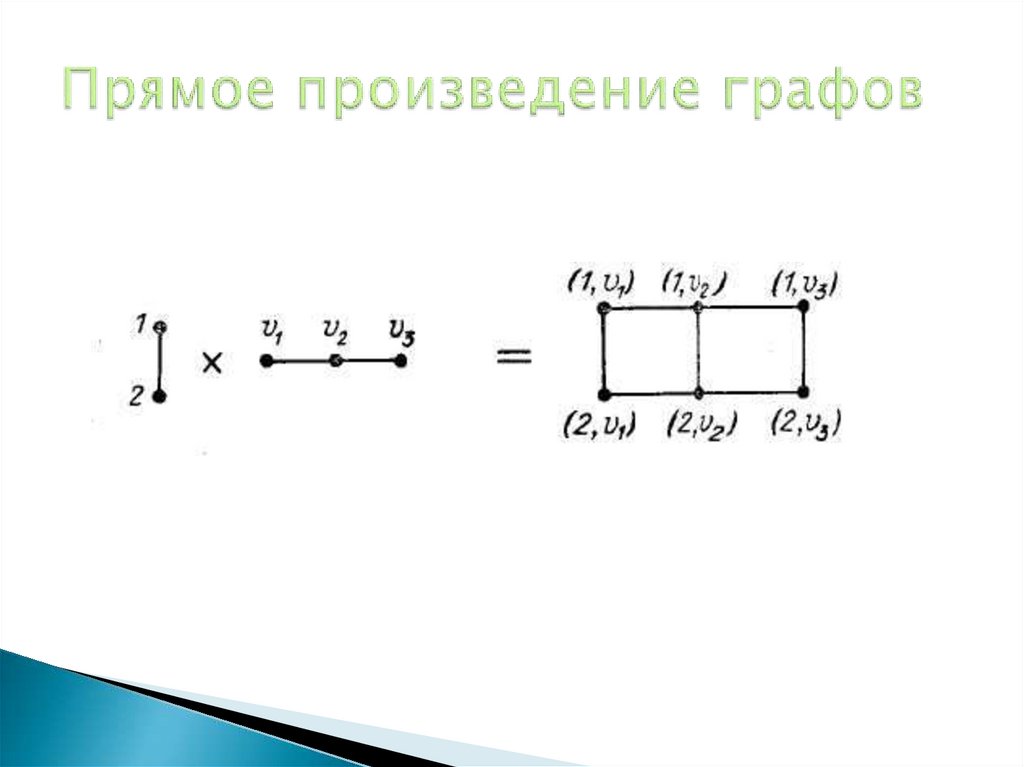
Объединение графов

27. Прямое произведение графов

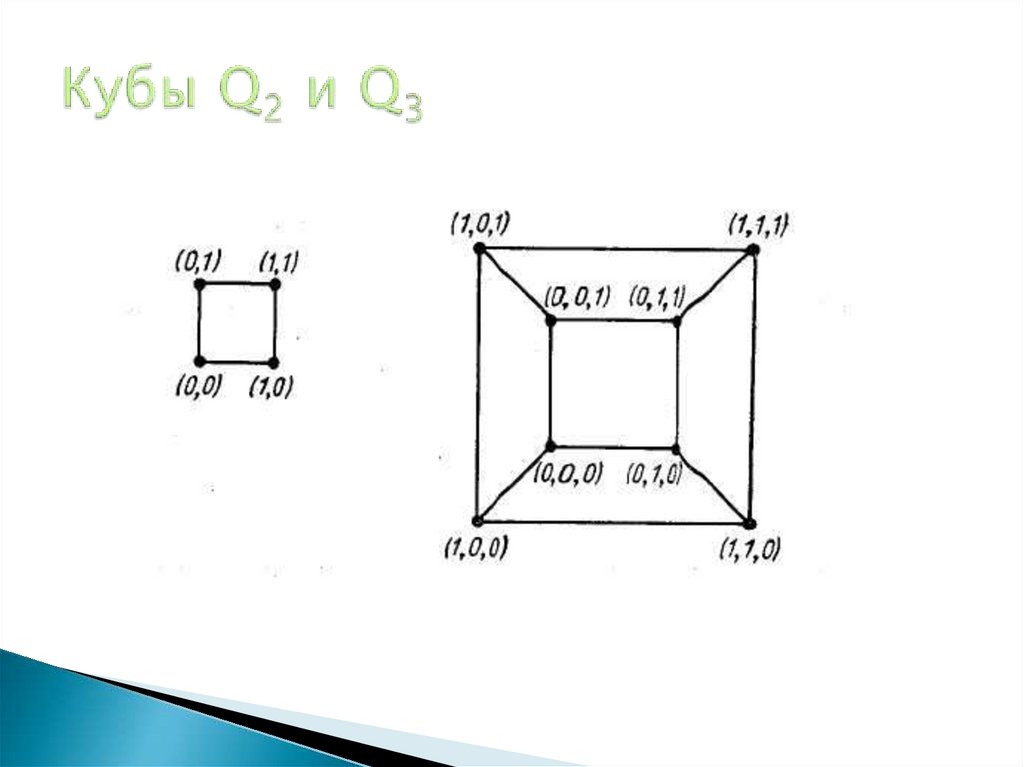
28. Кубы Q2 и Q3

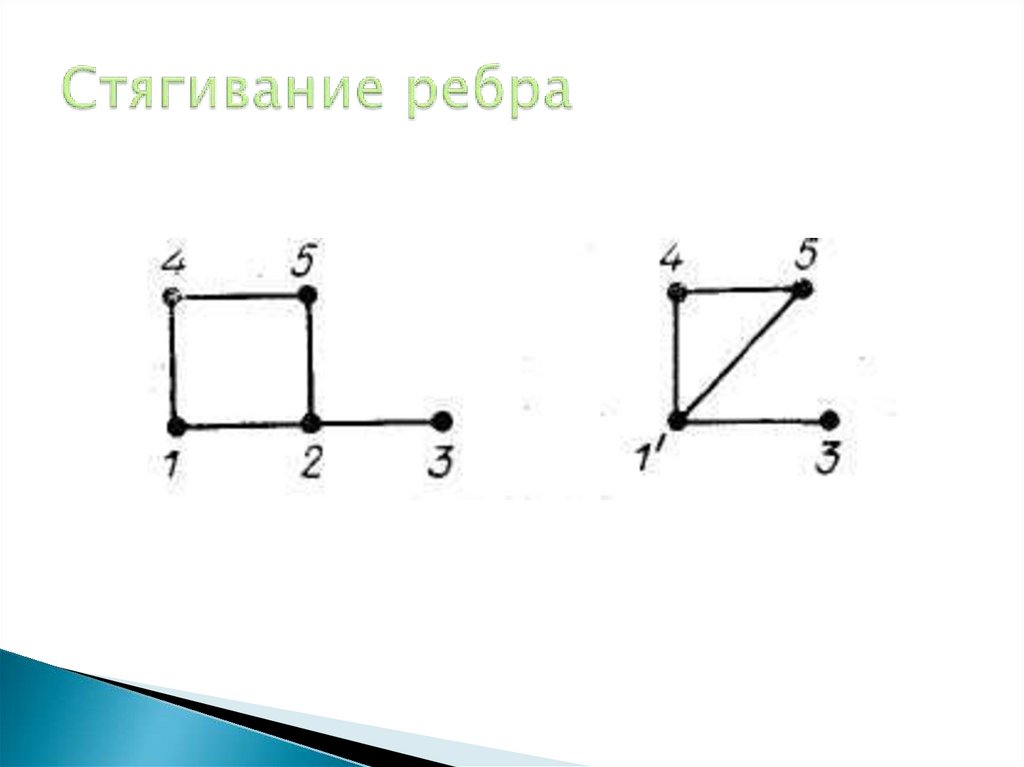
29. Стягивание ребра

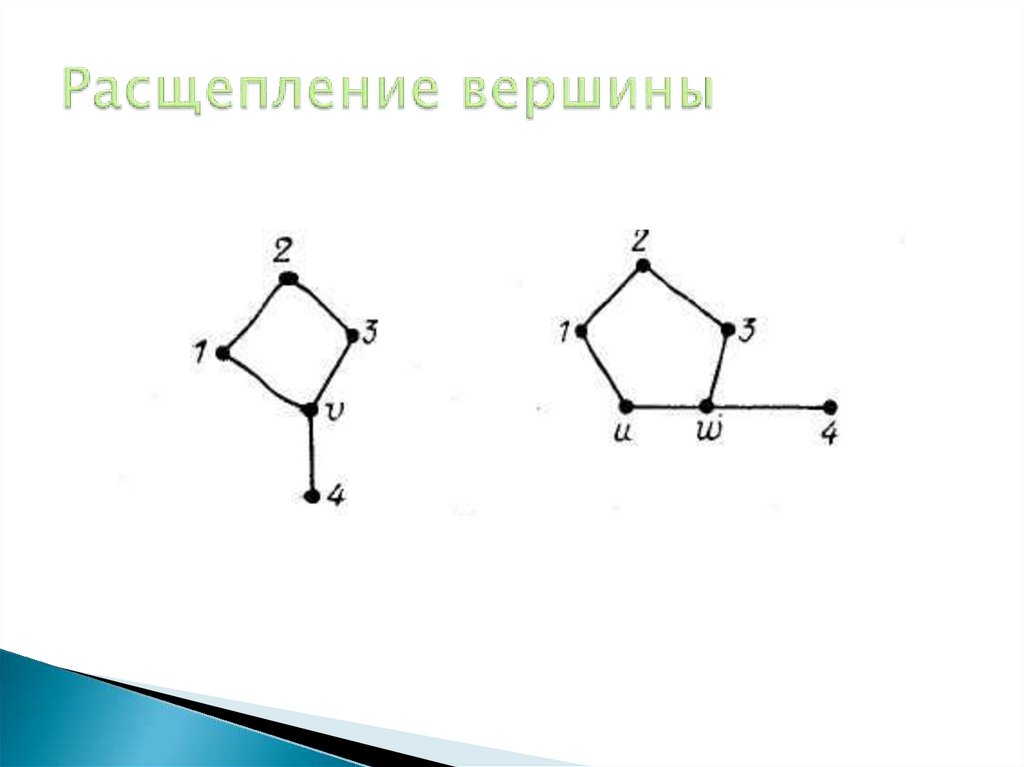
30. Расщепление вершины

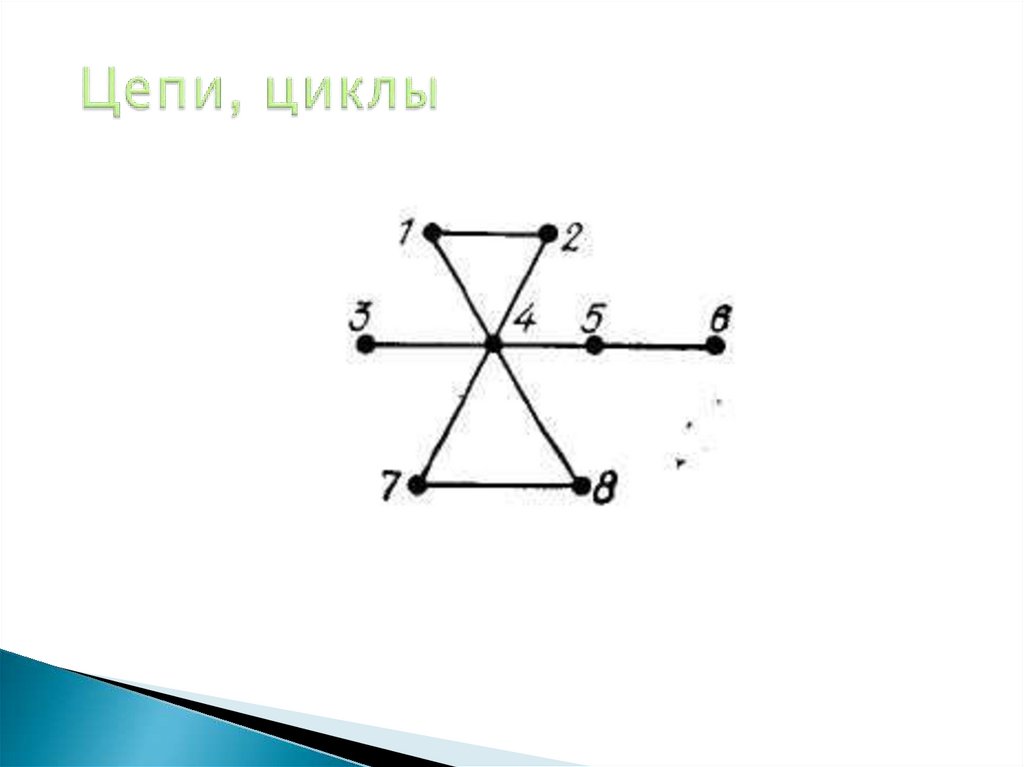
31. Цепи, циклы

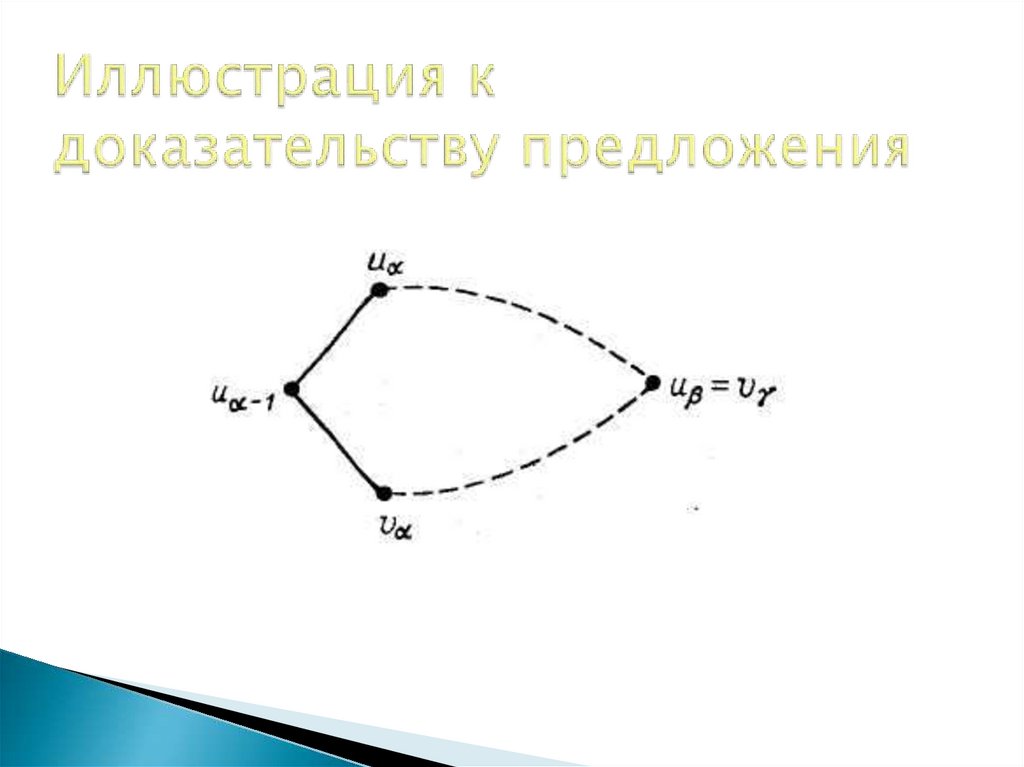
32. Предложения

Объединение двух несовпадающих простых
цепей содержит простой цикл.
Если С и D – два несовпадающих простых
цикла графа G, имеющих общее ребро е, то
граф G\e также содержит простой цикл.

33. Иллюстрация к доказательству предложения

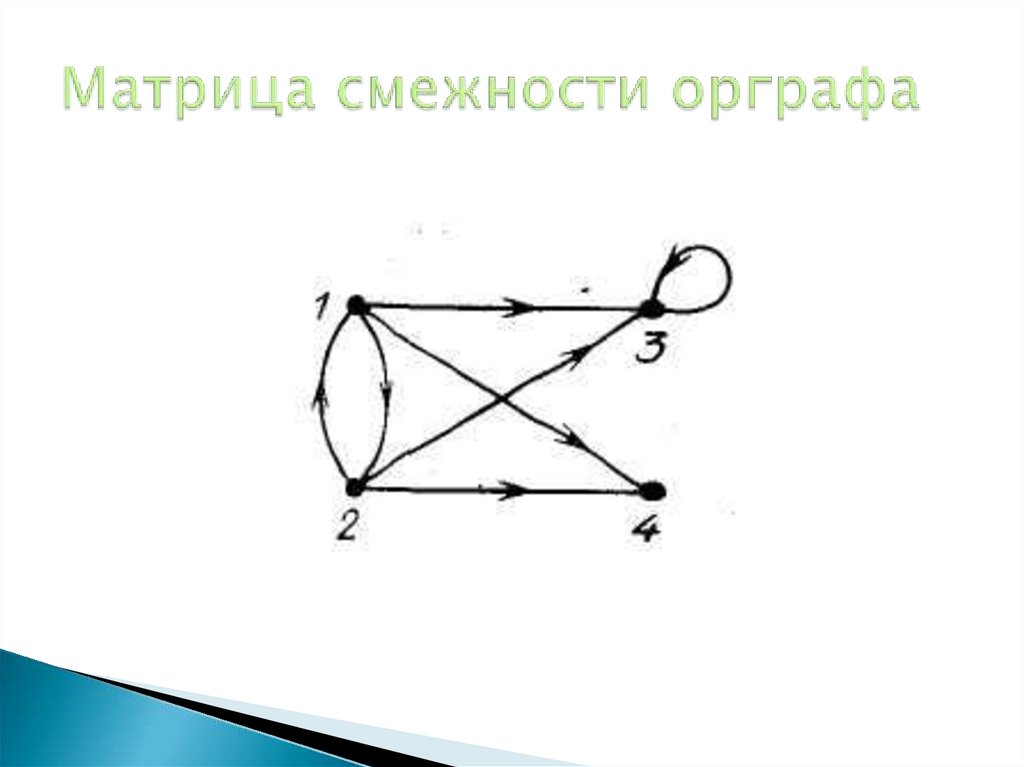
34. Матрица смежности орграфа

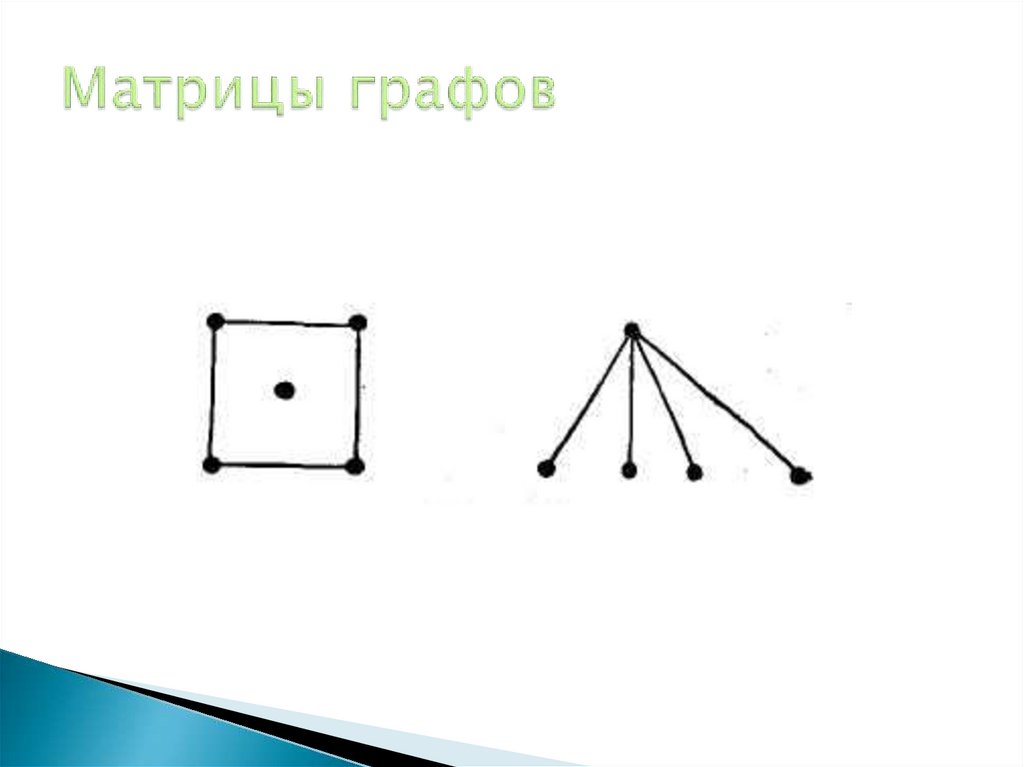
35. Матрицы графов

36. Регулярный граф

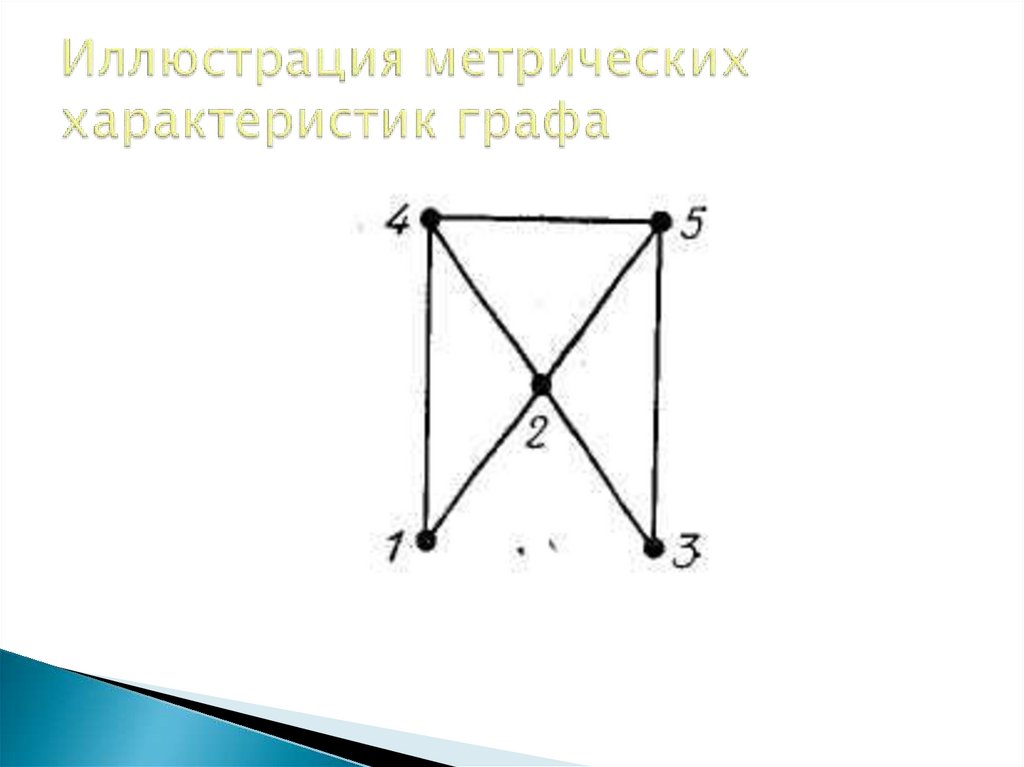
37. Иллюстрация метрических характеристик графа

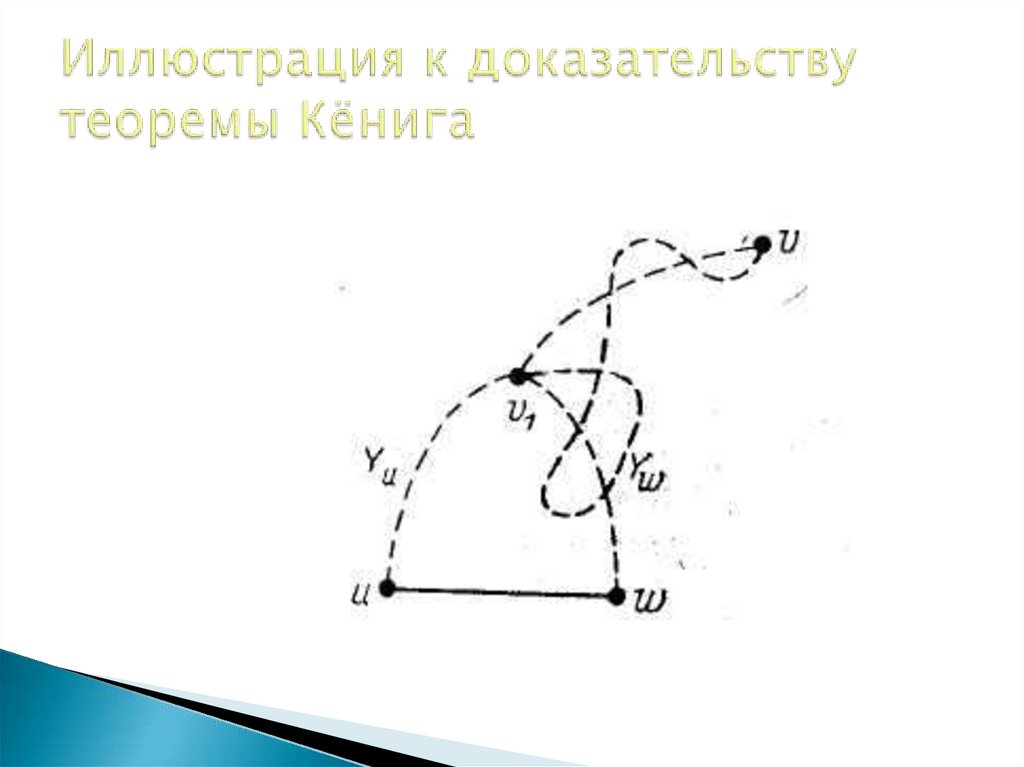
38. Теорема Кёнига

Граф является двудольным тогда и только
тогда, когда он не содержит цикла нечётной
длины.