Похожие презентации:
Основные физические величины и их единицы измерения
1. Определи тему урока
•Температура•Масса
•Сила тока
•Напряжение
•Давление
•Сила
•Время
•Кельвин
•Метр
•Секунда
•Паскаль
•Ньютон
•Вольт
•Ватт
2. Основные физические величины и их единицы измерения
04/09/253. Цели обучения
• 10.1.1.1 - представлять производные единицы измерения физических величин через основныеединицы измерения СИ;
4.
Международная система единиц СИОсновные единицы
измерения
Производные
единицы измерения
5.
Существует только определенноеколичество основных единиц в
СИ.
Сколько их вы знаете ?
Назовите их ?
6.
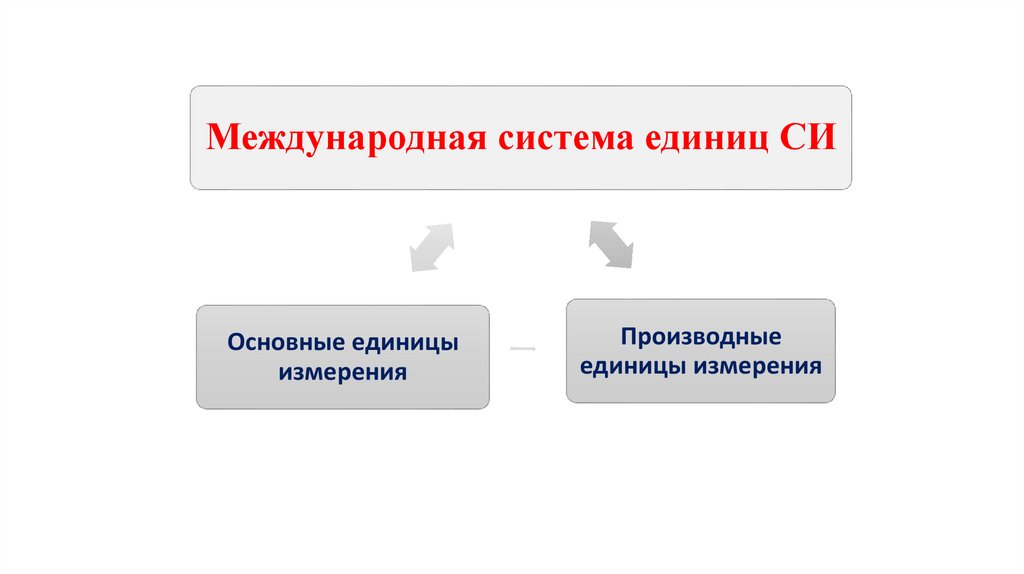
7. Основные единицы Международной системы единиц (СИ) – семь единиц измерения основных величин Международной системы величин,
Основные единицы Международной системыединиц (СИ) – семь единиц измерения основных
величин Международной системы величин,
принятые Генеральной конференцией по мерам и весам.
8.
•Критерии оценивания:Учащийся достиг цели обучения, если…
Знает основные физические величины СИ;
Переводит внесистемные единицы в систему СИ;
Переводит производные единицы измерения в основные
единицы;
Производит вычисления и записывает результат с учетом
значащих цифр.
Верно произвел измерения и систематизировал данные в
таблицу.
9.
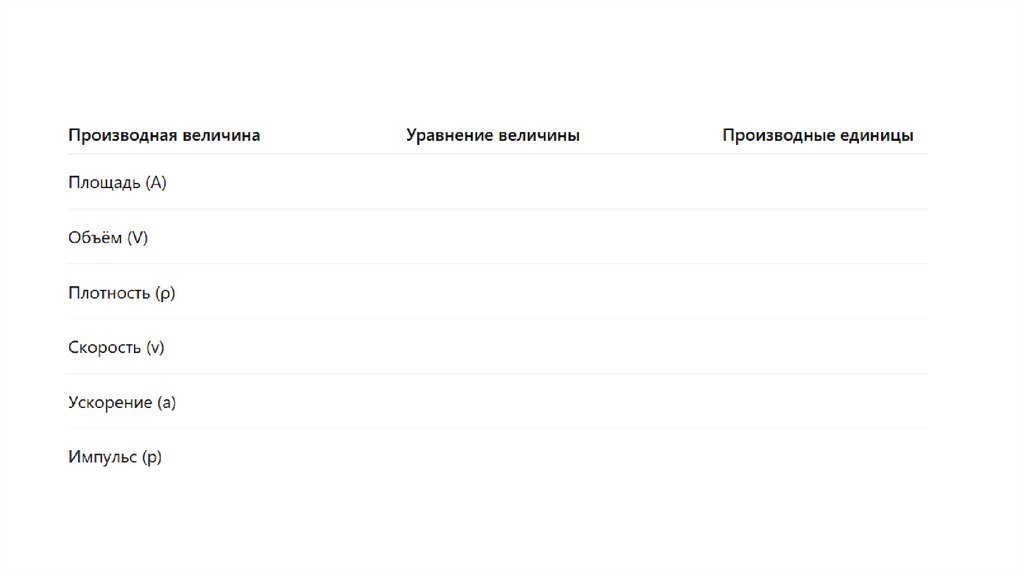
Производные единицы измеренияПочему единица скорости является
производной единицей измерения?
м/с
10.
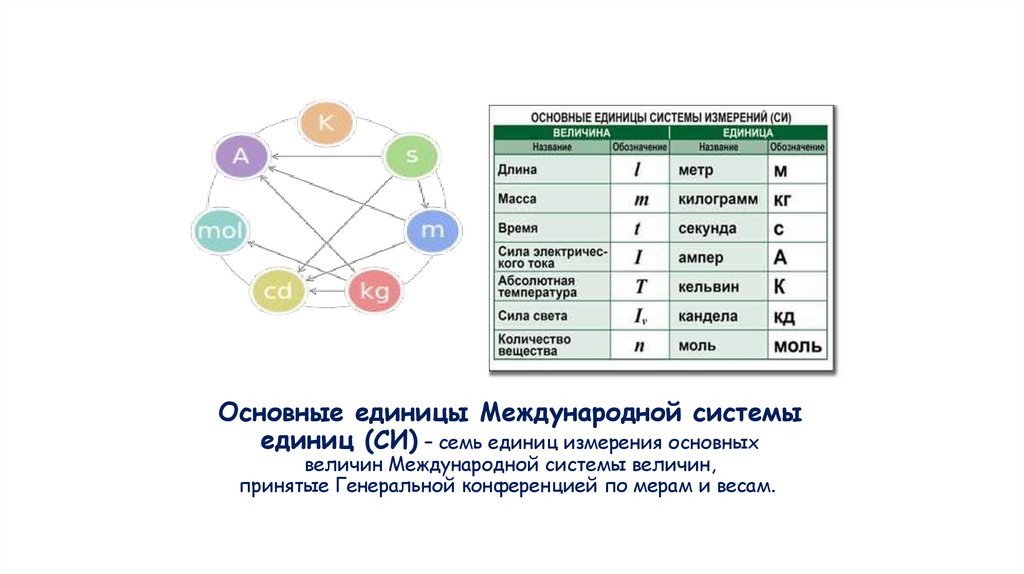
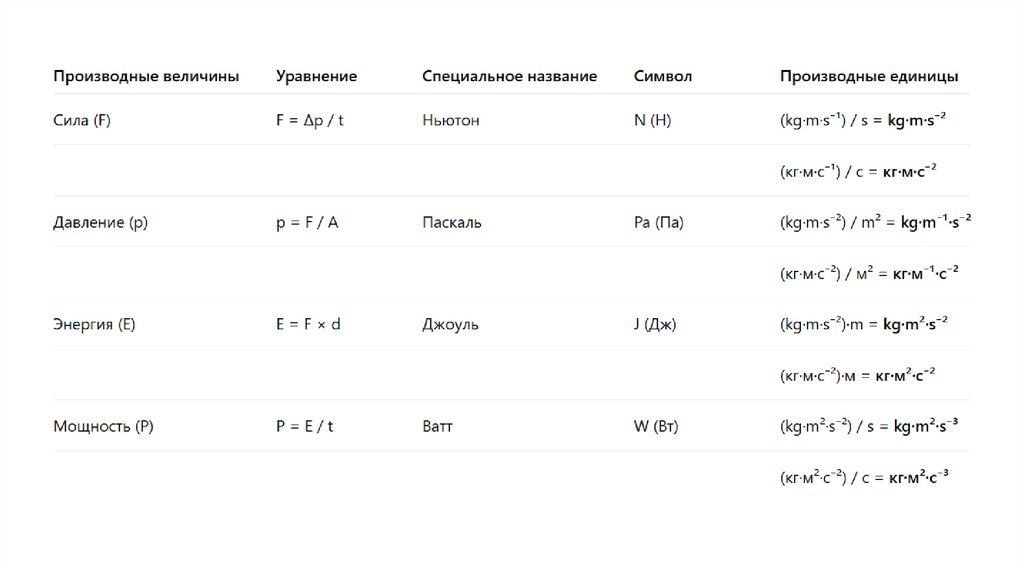
Ep = m g hДж = кг Н кг-1 м
Н м = кг кг м с-2кг-1 м
кг м с-2 м = кг м2с-2
кг м2с-2 = кг м2с-2
11.
12.
13.
14.
15.
16.
17.
18. Необходимость получения точных данных Значащие цифры
19. Учебные цели
• 10.1.1.3* - объяснять необходимость получения точных данных;• 10.1.1.2* - определять количество значащих цифр и знаков после запятой;
20. Значащие цифры
•Значащими называются все цифры, кроменуля ,а также и ноль в том случае, если он
стоит между другими значащими цифрами.
21.
Правила для значимых чиселПравило № 1
Все ненулевые цифры ВСЕГДА значимы.
Значащие цифры десятичного числа – это все его
цифры, начиная с первой ненулевой слева.
Пример :
x = 0.002036, цифры 2036 являются значащими;
x = 2.27×106,
значащими цифрами являются цифры 2, 2, 7;
x = 2270000,
все цифры этого числа являются значащими.
22.
Правило №2Все нули между значащими цифрами ВСЕГДА значимы.
Сколько значащих цифр в следующих числах?
504
3
60002
5
4
9.077
23.
Правило № 3Все конечные нули справа от десятичного знака значащие.
Сколько значащих цифр в следующих числах?
32.0
3
19.000
5
105.0020
7
24.
Правило № 4Все нули, которые действуют как заполнители, НЕ
являются значимыми.
Нули значимы только в том случае, если они находятся
между значащими цифрами, ИЛИ являются самой
последней вещью в конце десятичной дроби.
25. Определите число значащих цифр
•3,240•0,0372
•13,7
•1,37
•0,137
•0,0137
26. Ответы
• 3,240 (4)• 0,0372 (3)
• 13,7 (3)
• 1,37 (3)
• 0,137 (3)
• 0,0137 (3)
27.
Сколько значащих цифр в следующих числах?0.0002
1
6.02 x 1023
3
100.000
6
150000
2
800
1
28. Правила при вычислениях
• Сложение и вычитаниеРезультат должен содержать столько десятичных знаков, сколько их меньше в исходных
данных.
Пример:
• 12,45 + 3,4 = 15,9 (один знак после запятой, как у 3,4).
• 12,45 + 3,4 = 15,9(у 12,45 два знака после запятой, у 3,4 – один → ответ с одним знаком).
• 125,3 – 24,12 = 101,2(125,3 имеет один знак после запятой, 24,12 – два → результат
округляем до одного).
• 5,678 + 4,32 = 10,00(5,678 имеет три знака, 4,32 – два → результат с двумя знаками: 10,00).
• 0,0065 + 0,00042 = 0,0069(0,0065 имеет 4 знака после запятой, 0,00042 – 5 → берём 4, так как
их меньше → 0,0069).
• 150,0 – 0,365 = 149,6(150,0 имеет один знак после запятой, 0,365 – три → ответ округляем до
одного).
29. Умножение и деление
• Результат должен содержать столько значимых цифр, сколько их меньше в исходныхданных.
• Пример:
• (2,34 · 1,2) = 2,8 (2 ЗЦ, так как 1,2 имеет 2 ЗЦ).
• 2,34 × 1,2 = 2,8(2 ЗЦ → как у 1,2).
• 15,8 ÷ 3,42 = 4,62 → 4,62(оба числа имеют 3 ЗЦ → оставляем 3 ЗЦ).
• 4,56 × 0,020 = 0,0912 → 0,091(4,56 = 3 ЗЦ, 0,020 = 2 ЗЦ → ответ с 2 ЗЦ).
• 125 ÷ 2,5 = 50 → 50(125 = 3 ЗЦ, 2,5 = 2 ЗЦ → ответ с 2 ЗЦ, поэтому просто 50).6,022 × 10²³
÷ 2 = 3,011 × 10²³ → 3 × 10²³(6,022 = 4 ЗЦ, 2 = 1 ЗЦ → результат с 1 ЗЦ).
30. Возведение в степень и корень
• Количество значимых цифр сохраняется.Пример:
• √2,56 = 1,60 (3 ЗЦ).
31. Человеческая ошибка
• Профессор Мэссер решил измеритьдлину деревянной линейки с помощью
рулетки.
• Обсудите: Что он сделал неправильно?
Сколько ошибок вы нашли?
32. Ошибки профессора Мэссера:
•Измерение начато со стороны 100 деления линейки.•95,4 — неправильное число.
•мм — неверная единица измерения (нужно см).
•Линейка в руке может смещаться и двигаться.
•Между деревянным предметом и линейкой есть зазор.
•Начало предмета не совпадает с началом линейки.
•Глаза расположены неправильно (параллакс).
•Он стоит не с той стороны линейки, чтобы правильно видеть показания.
33. Типы ошибок
✔ Систематические ошибки:Возникают из-за неправильно откалиброванного прибора (нулевая ошибка) или из-за неверного
метода измерения.
✔ Случайные ошибки:
Возникают из-за изменений температуры, вибрации, землетрясения, ветра и других факторов,
которые невозможно заранее предсказать.
К случайным ошибкам относятся также ошибки экспериментатора: неправильный угол зрения
(параллакс), ограниченность слуха или зрения и др.
Такие ошибки связаны с непостоянными внешними условиями или особенностями объекта
измерения.
✔ Абсолютная ошибка:
Выражается формулой и показывает разность между измеренным и истинным значением (в
абсолютных единицах).
✔ Относительная ошибка:
Показывает, насколько измеренное значение отличается от истинного в сравнении с самим
значением величины (выражается в долях или процентах).
34. Абсолютная погрешность
• Абсолютная погрешность показывает, насколько измеренное значение можетотличаться от истинного в тех же единицах, что и сама величина.


































 Физика
Физика