Похожие презентации:
Конструкции фундаментов под машины
1.
3. Импульсные нагрузки от машин ударного действия(кузнечные молоты, копры, формовочные машины)
Q0
I m0 v0
v0 ,
g
где v0
– скорость падения ударной части;
m0, Q0 – масса и вес ударной части, соответственно;
g
– ускорение свободного падения.
2.
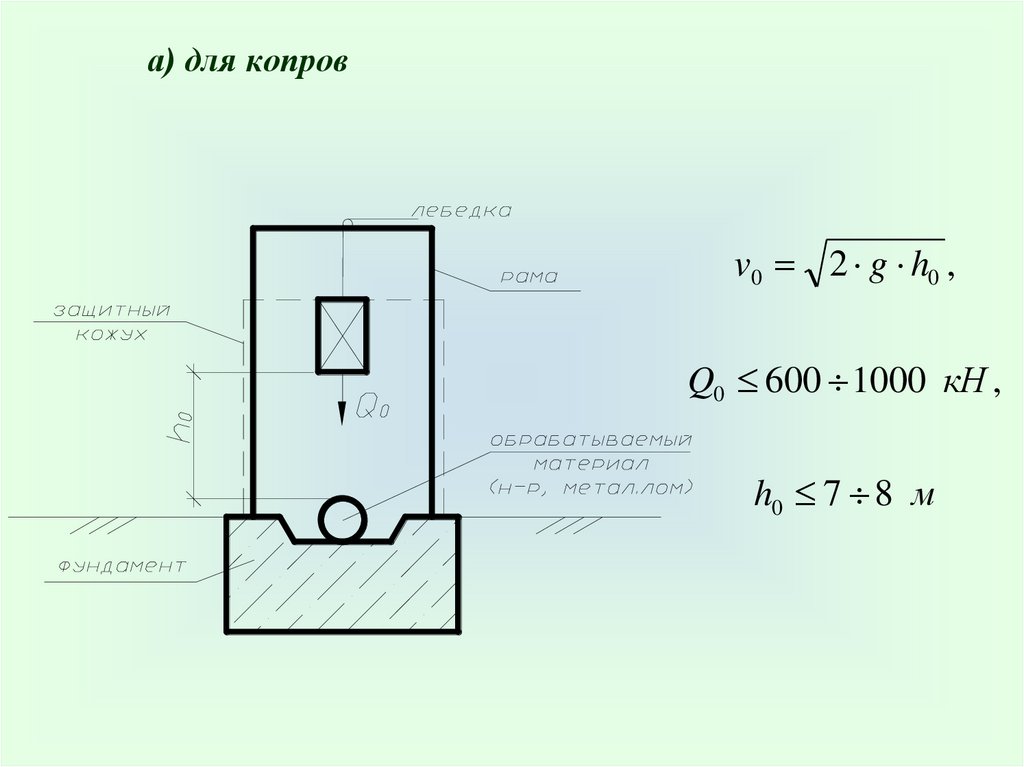
а) для копровv0 2 g h0 ,
Q0 600 1000 кН ,
h0 7 8 м
3.
4.
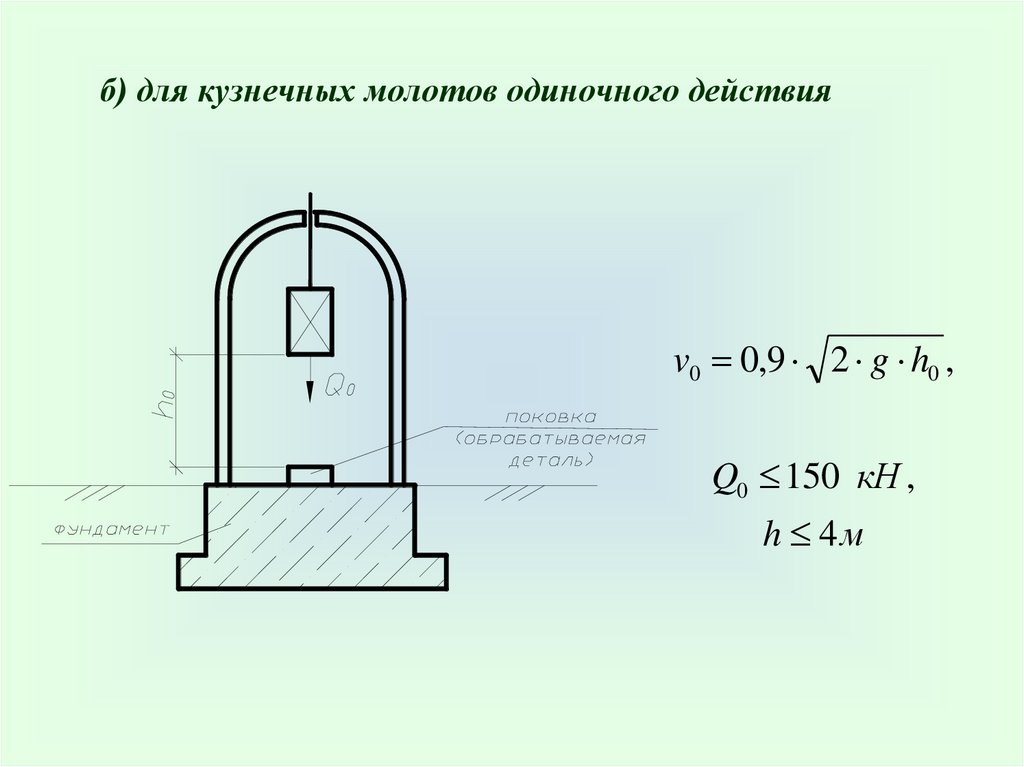
б) для кузнечных молотов одиночного действияv0 0,9 2 g h0 ,
Q0 150 кН ,
h 4м
5.
6.
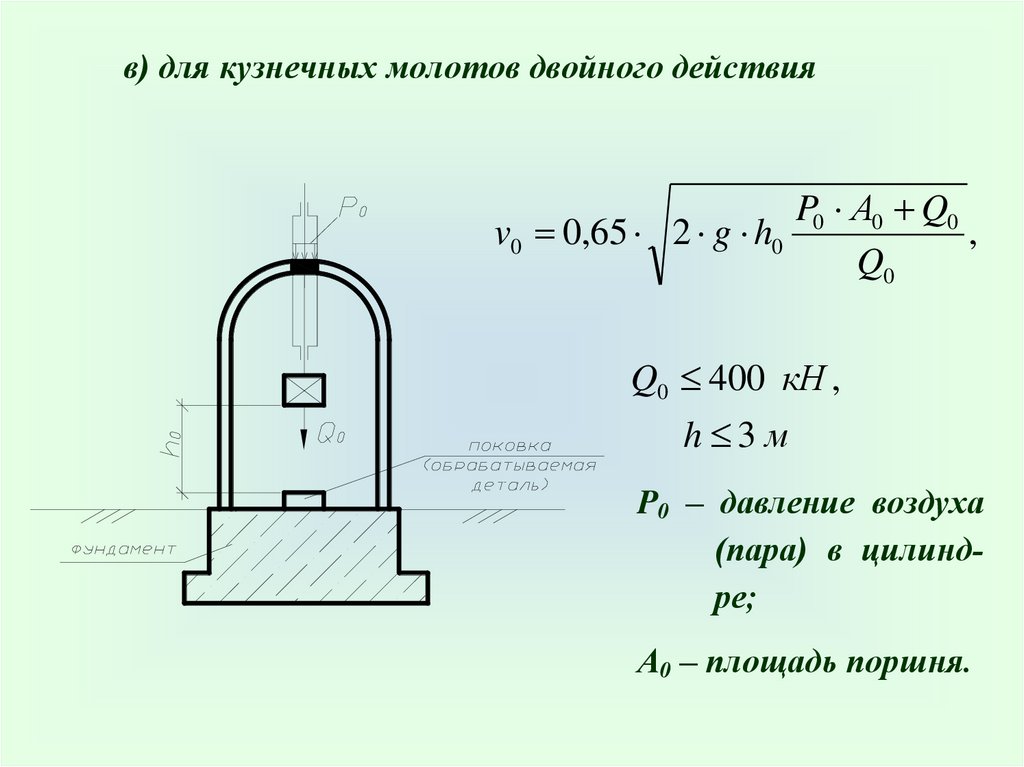
в) для кузнечных молотов двойного действияP0 А0 Q0
v0 0,65 2 g h0
,
Q0
Q0 400 кН ,
h 3м
P0 – давление воздуха
(пара) в цилиндре;
А0 – площадь поршня.
7.
Конструкциифундаментов
под машины
8.
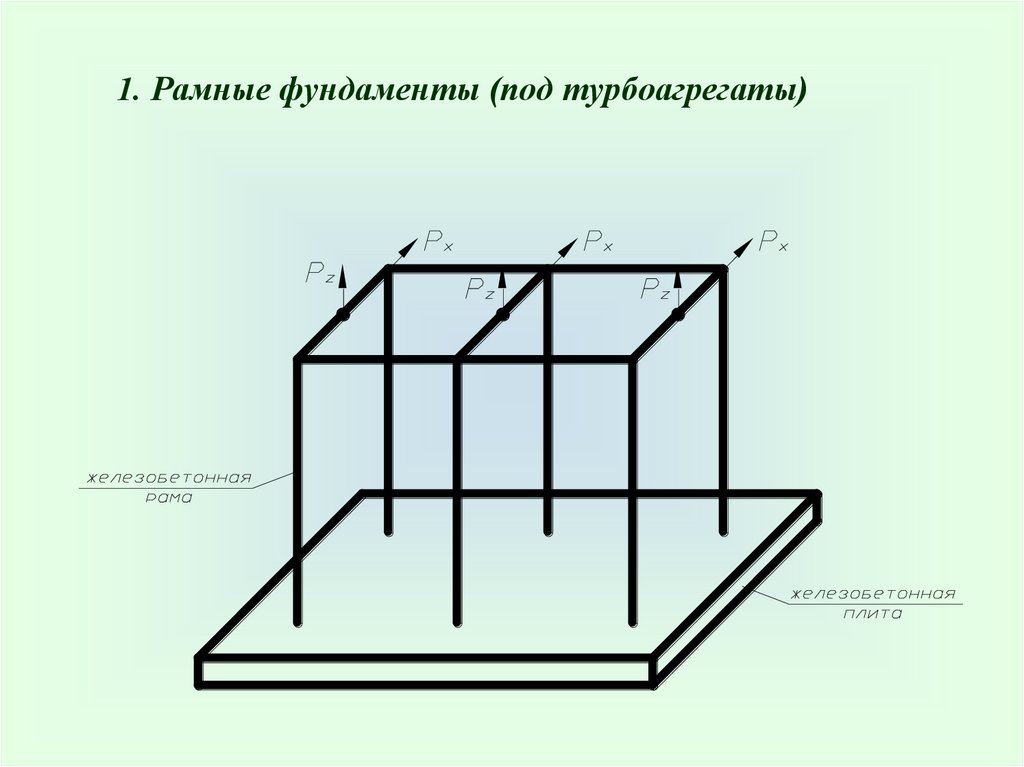
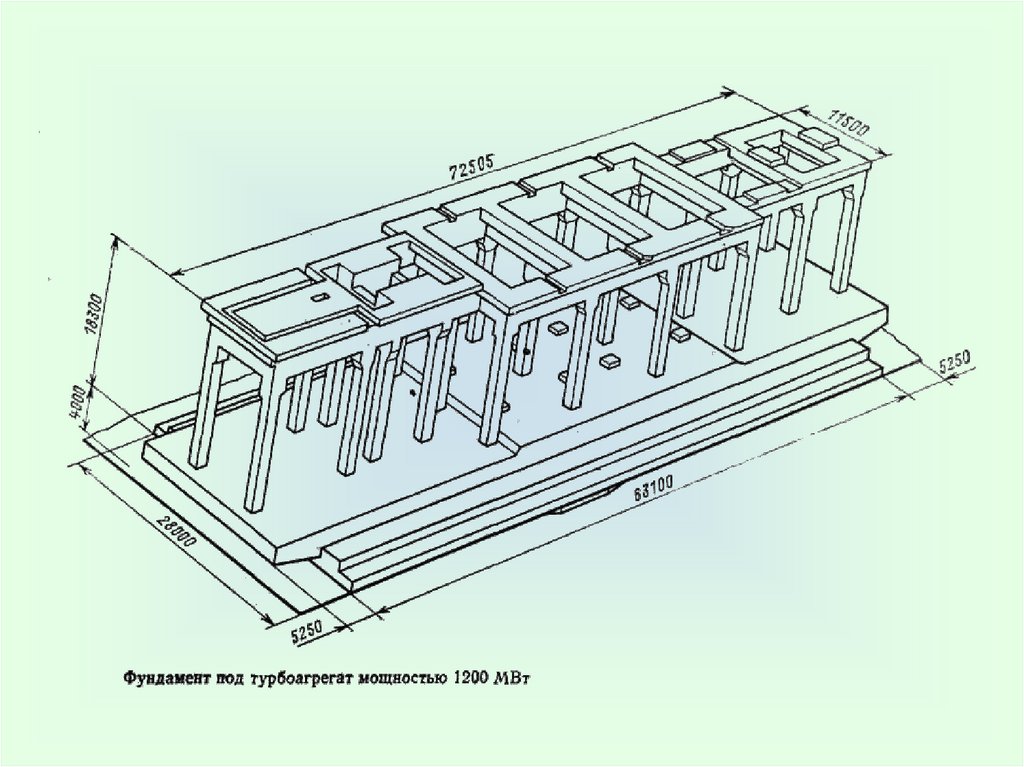
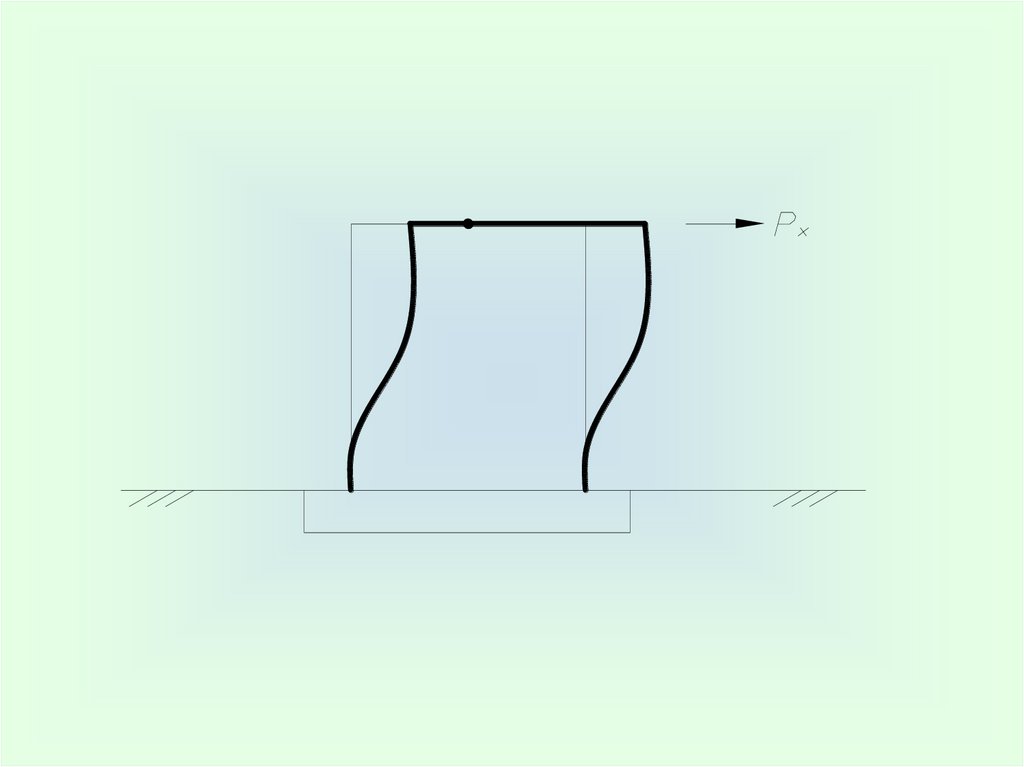
1. Рамные фундаменты (под турбоагрегаты)9.
10.
11.
12.
13.
14.
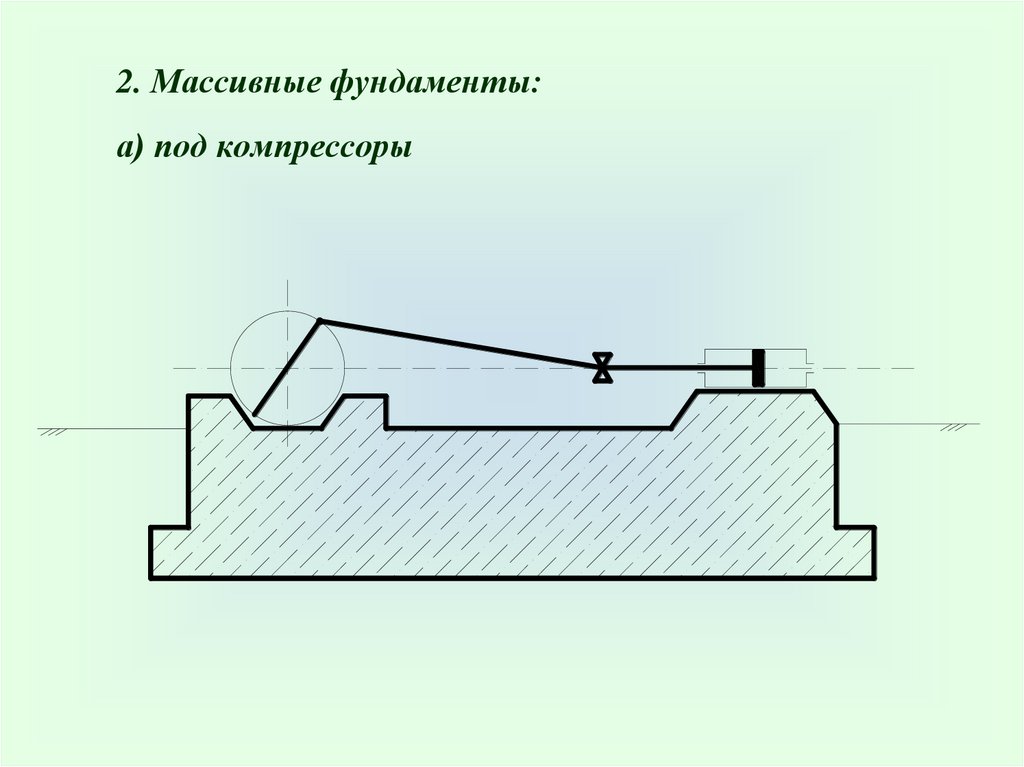
2. Массивные фундаменты:а) под компрессоры
15.
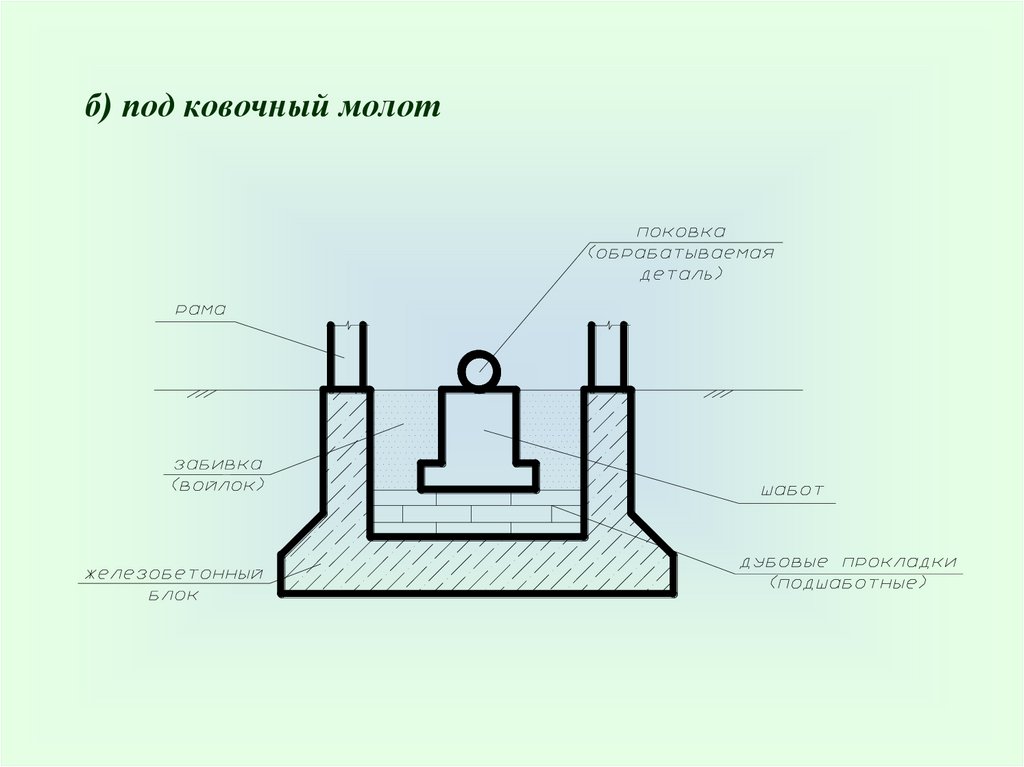
б) под ковочный молот16.
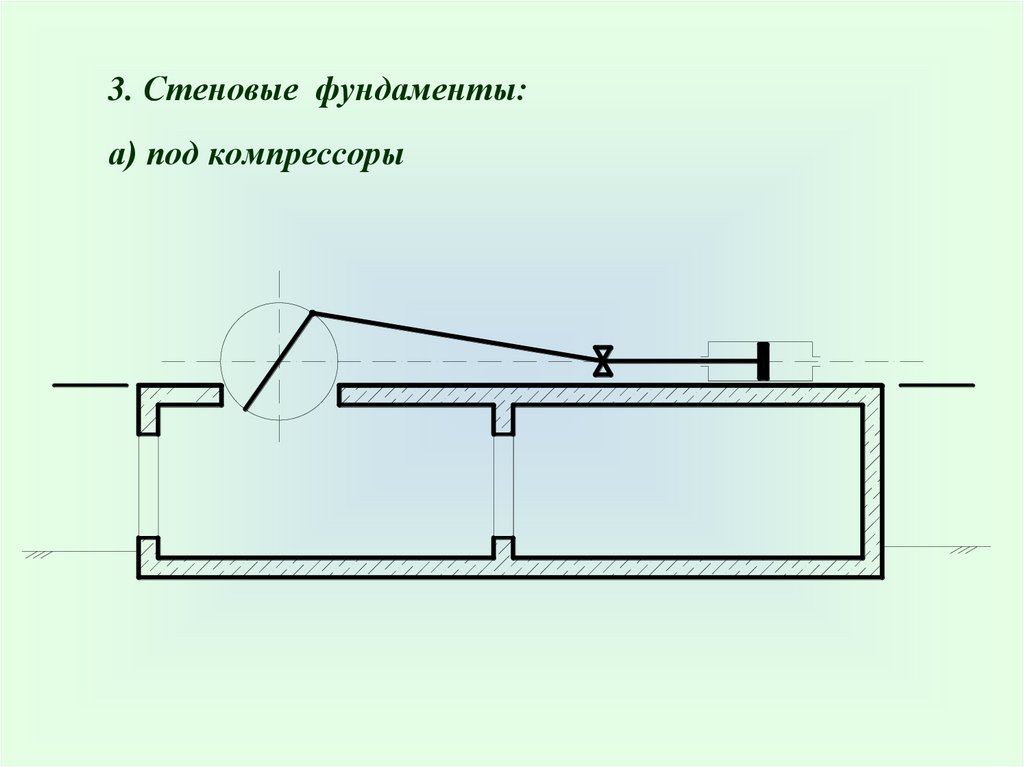
3. Стеновые фундаменты:а) под компрессоры
17.
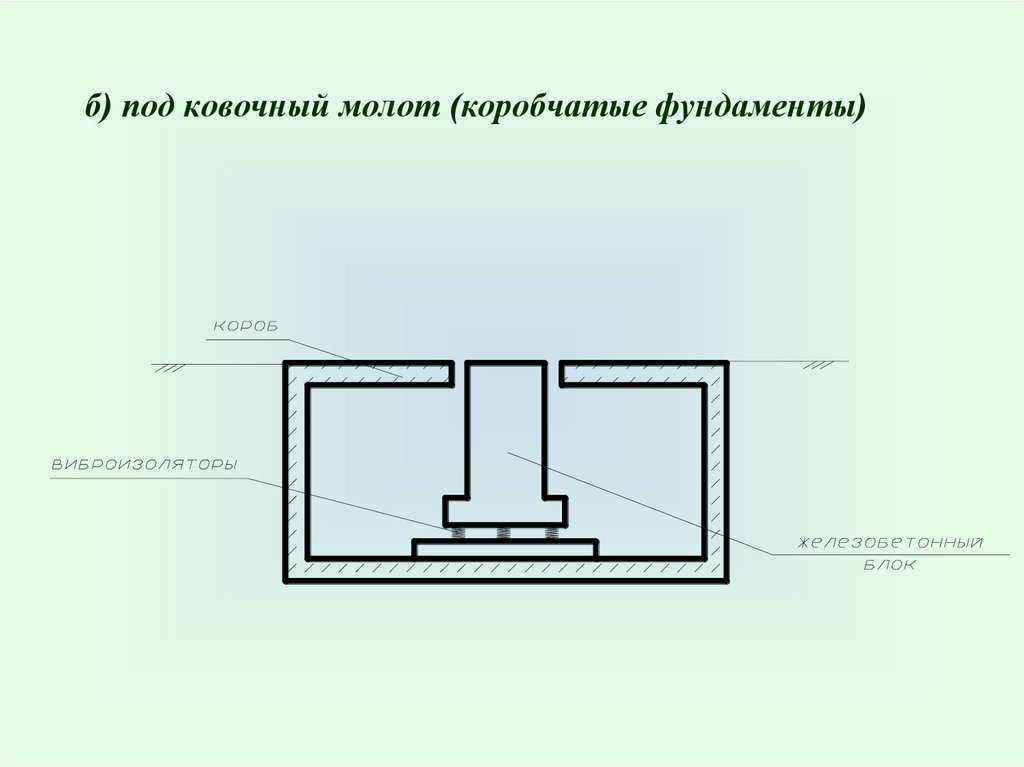
б) под ковочный молот (коробчатые фундаменты)18.
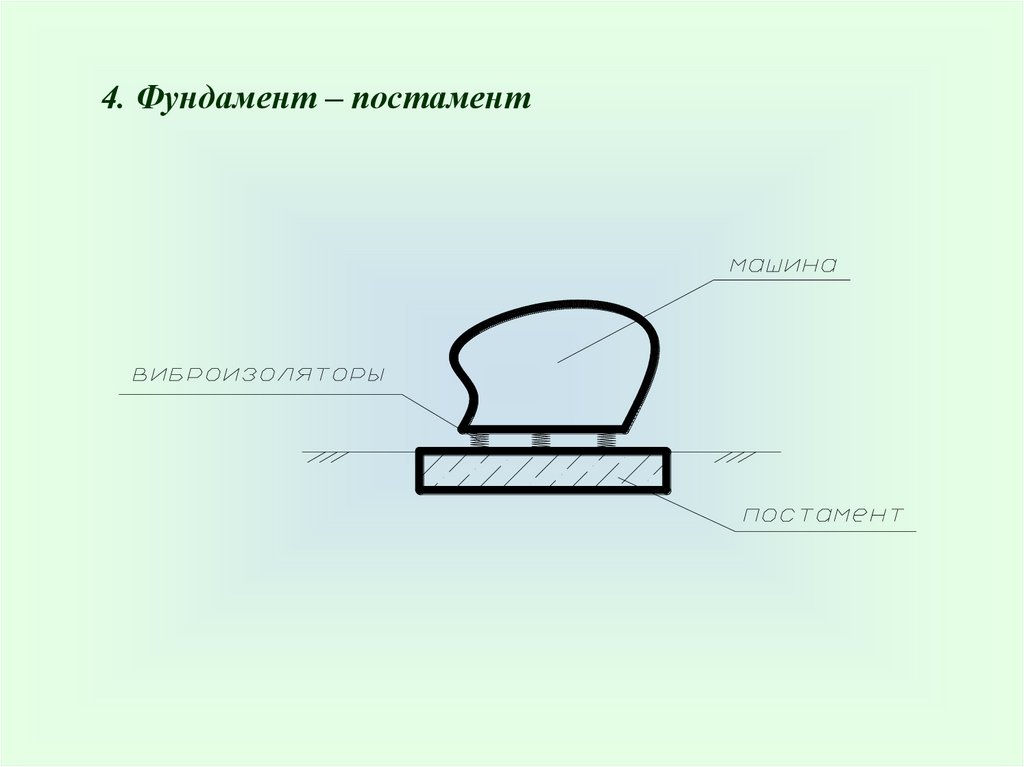
4. Фундамент – постамент19.
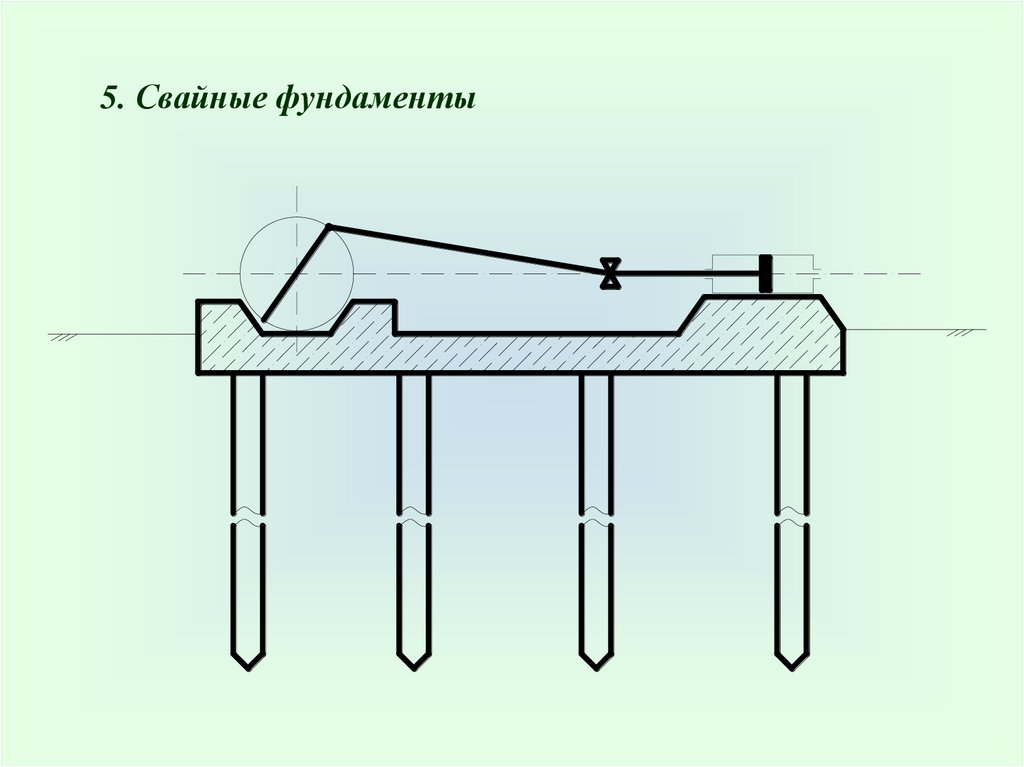
5. Свайные фундаменты20.
Принципырасчета
фундаментов
под машины
(в соответствии с СП 26.13330.2012.
Актуализированная версия СНиП 2.02.05-87
«Фундаменты с динамическими нагрузками»)
21.
1) Рср с 0 с1 R,где γс0 – коэффициент условия работы, учитывающий
характер динамических нагрузок и ответственность машин
(γс0 = 0,5 – для молотов, формовочных машин,
γс0 = 0,8 – для дробилок, мельниц, компрессоров);
γс1 – коэффициент условия работы грунтового основания (γс1 = 1,0 или γс1 = 0,7);
22.
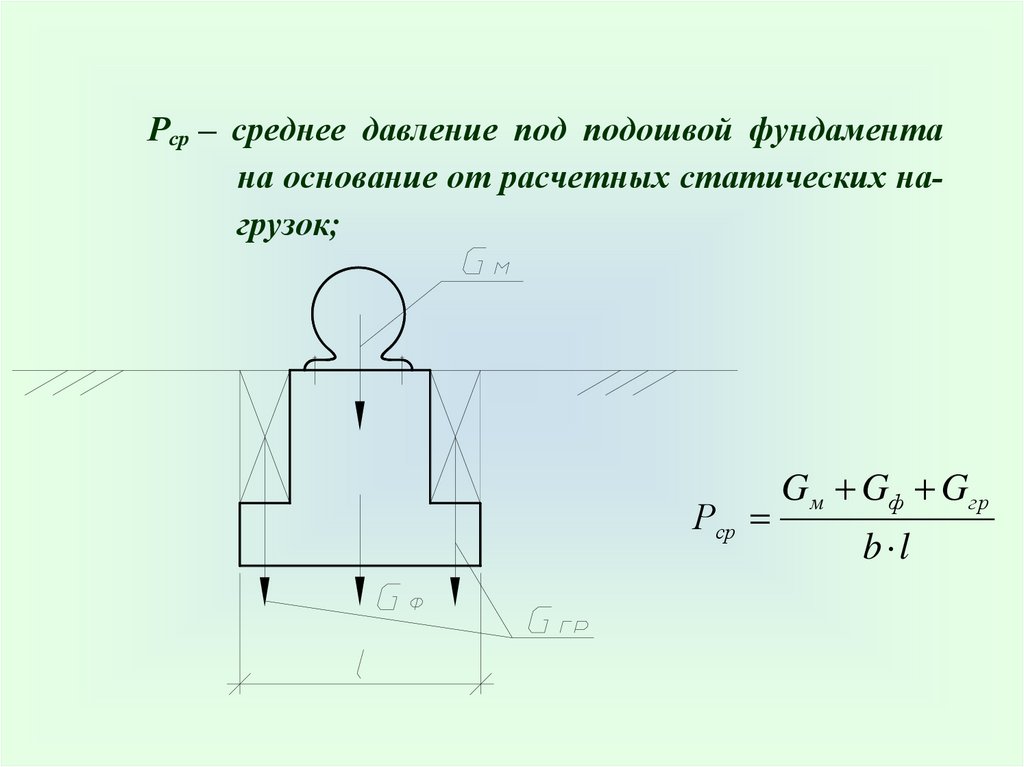
Рср – среднее давление под подошвой фундаментана основание от расчетных статических нагрузок;
Рср
G м Gф Gгр
b l
23.
RRусл
– расчетное сопротивление основания.
c1 c 2
k
M k z b II M q d II/ M q 1 d b II/ M c cII
24.
2) а аи ,где а – наибольшая амплитуда колебаний фундамента, определяется расчетом;
например,
для машин с импульсной нагрузкой (молоты и т.п.):
(без учета затухания колебаний)
аz
1 I
m z
,
аz – наибольшая амплитуда колебаний фундамента при импульсной нагрузке;
25.
I– импульс силы ( I m0 v );
m – масса системы;
λz – частота свободных колебаний (собственных);
ε
– коэффициент восстановления удара.
аи – максимально допустимая амплитуда колебаний фундамента, принимается по СП
26.13330.2012 (зависит от вида машины и
частоты колебаний) или по тех.паспорту
машины.
26.
Для машин с равномерным вращением:n = 1000 ÷ 750 об/мин
аи = 0,06 ÷ 0,10 мм;
n = 750 ÷ 500 об/мин
аи = 0,10 ÷ 0,15 мм;
n < 500 об/мин
аи = 0,15 ÷ 0,20 мм.
27.
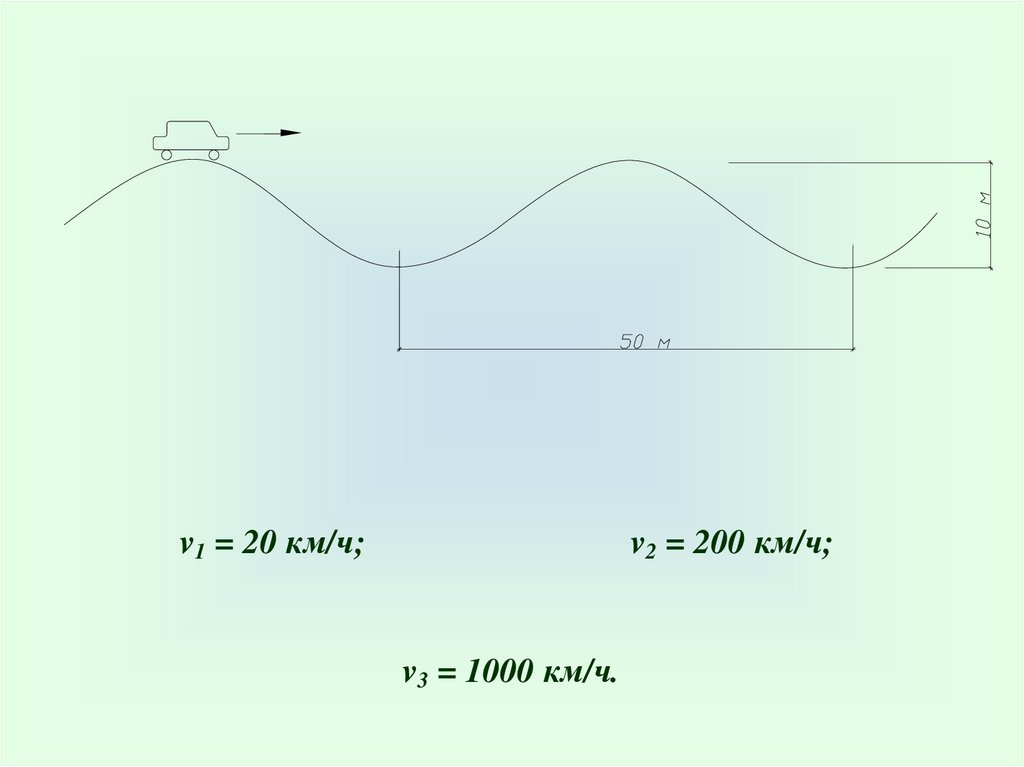
v1 = 20 км/ч;v2 = 200 км/ч;
v3 = 1000 км/ч.
28.
Вышеизложенные требования (допуски) относятся кколебаниям машин и их фундаментов.
Они распространяются и на другие объекты.
29.
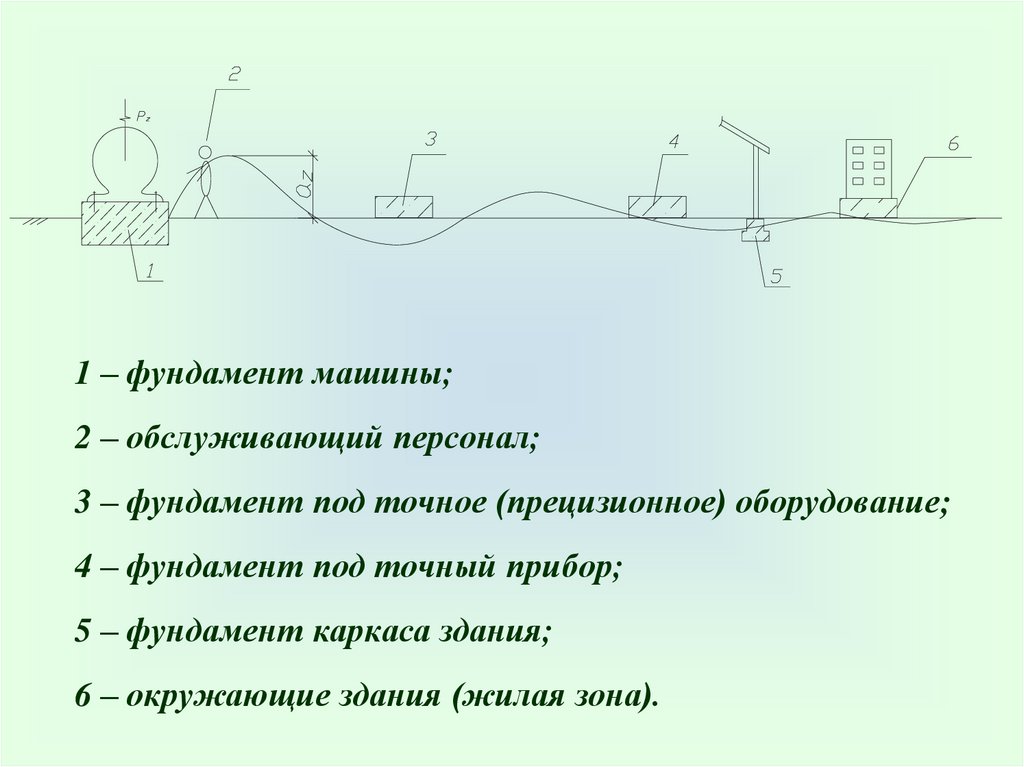
1 – фундамент машины;2 – обслуживающий персонал;
3 – фундамент под точное (прецизионное) оборудование;
4 – фундамент под точный прибор;
5 – фундамент каркаса здания;
6 – окружающие здания (жилая зона).
30.
Для рабочих мест, обслуживающего персонала:а ≤ [a],
по СН-245-71 «Санитарные нормы проек-
v ≤ [v],
тирования промпредприятий» (табл. 15)
ω ≤ [ω].
и ГОСТ 12.01.012-2004 «Вибрационная
безопасность. Общие требования».
а
– амплитуда (перемещение), мм;
v
– скорость перемещений, мм/сек;
ω
– ускорение перемещений, мм/сек 2;
[a], [v], [ω] – тоже предельно допустимые значения.
31.
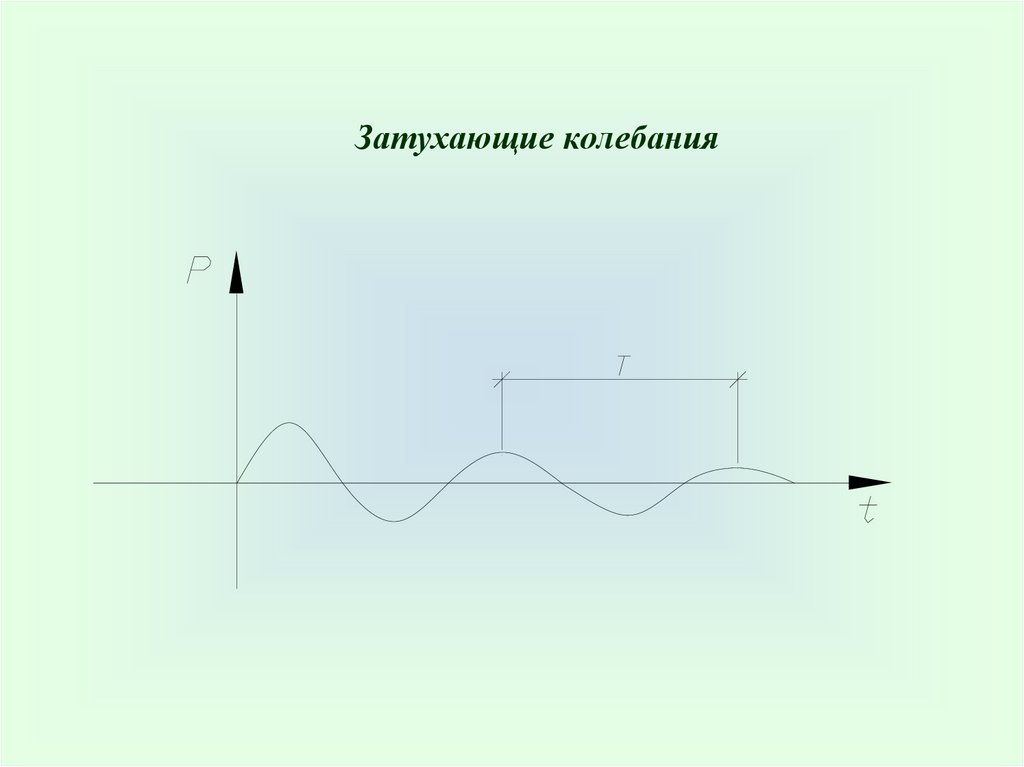
Затухающие колебания32.
Незатухающие колебания33.
v 2 f a,2 f 2 a,
1
f ,
T
где f – частота колебаний, Гц;
Т – период колебаний, сек.
34.
Для фундаментов под точное оборудование и приборы:а ≤ аи,
где а – амплитуда колебаний прецизионного оборудования или виброчувствительного прибора;
аи – предельно допустимая амплитуда колебаний,
зависящая от допуска на точность обработки детали или точность измерения.
35.
Для несущих конструкций зданий и их фундаментов:Мс + Мд ≤ Мвын.,
Nс + Nд ≤ Nвын.,
Qс + Qд ≤ Qвын.,
36.
где Мс , Nс, Qс – соответственно, изгибающий момент, сжимающая и поперечная нагрузки в элементах несущих конструкций от статических нагрузок;Мд, Nд, Qд – соответственно, изгибающий момент, сжимающая и поперечные нагрузки в элементах несущих конструкций от динамических нагрузок;
Мвын., Nвын., Qвын.
– соответственно, расчетные
изгибающий момент, сжимающая и
поперечная нагрузки (предельные) по
прочности и выносливости материала.
37.
Моделифундаментов и оснований,
используемые при расчете на колебания
38.
Характерным для всех моделей является то, чточасть колебательной системы рассматривается как
жесткое сплошное тело с массой, сосредоточенной в
точке (материальной точке).
39.
1. Модель Павлюка – Рауша(типа Винклера – Фойгта)
Свойства модели:
– инерционность грунта не учитывается (в действительности часть грунта колеблется с фундаментом);
– связь между реакциями грунта и перемещениями
фундамента считается линейной;
40.
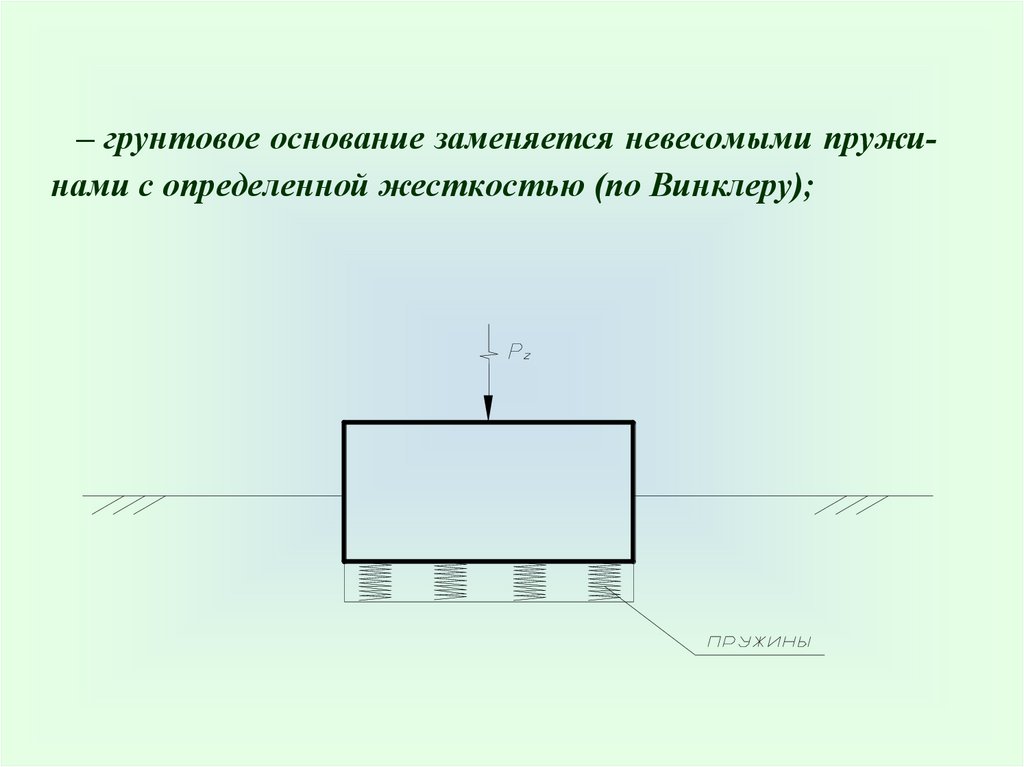
– грунтовое основание заменяется невесомыми пружинами с определенной жесткостью (по Винклеру);41.
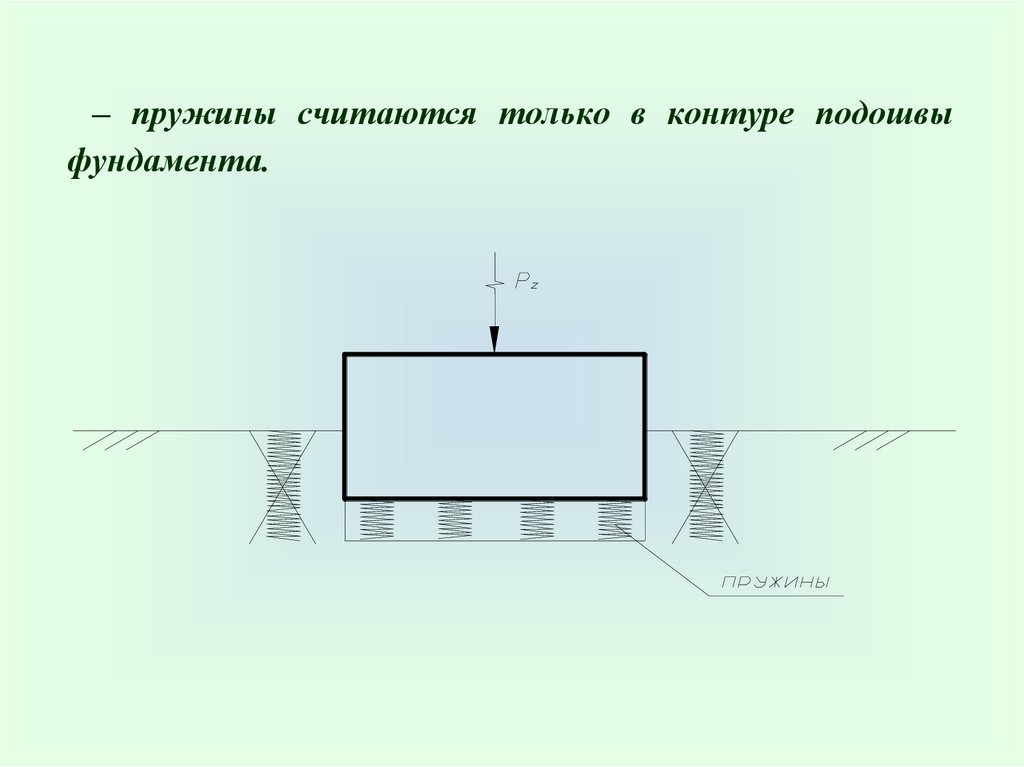
– пружины считаются только в контуре подошвыфундамента.
42.
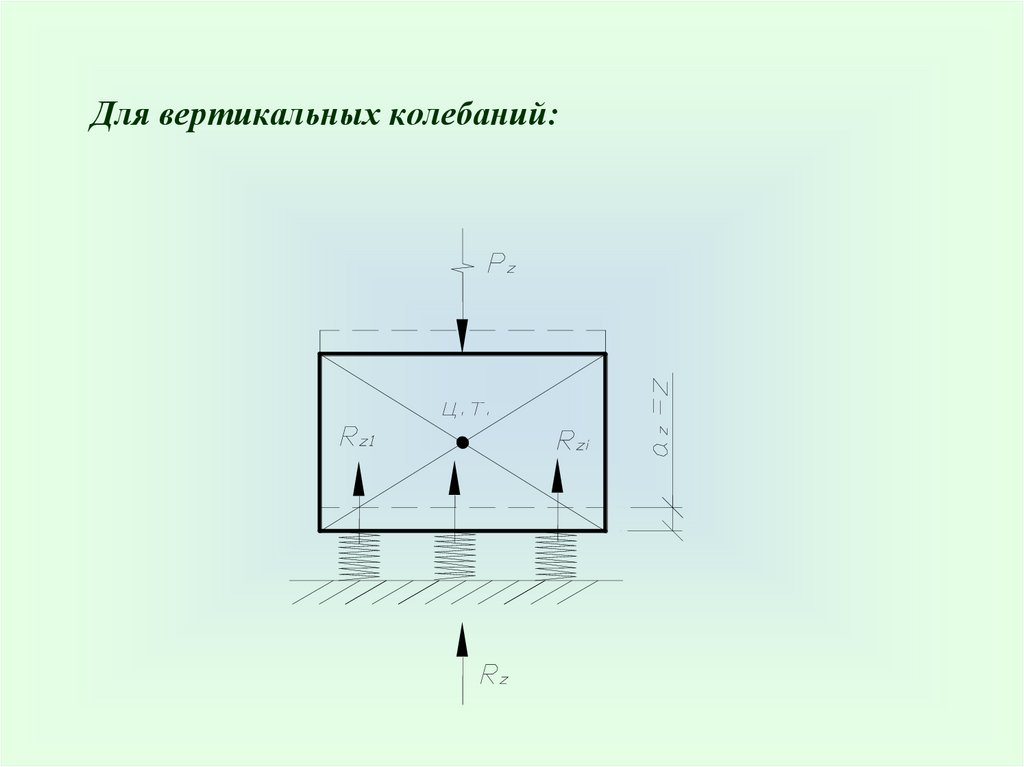
Для вертикальных колебаний:43.
R z – вертикальная реакция всех опор (пружин)Rz Rzi K z z,
K z C z А,
где Kz – общая жесткость пружин или основания при
сжатии;
Сz – жесткость условных пружин при сжатии,
распределенная по площади А или коэффициент упругого равномерного сжатия;
А
– площадь подошвы фундамента.
44.
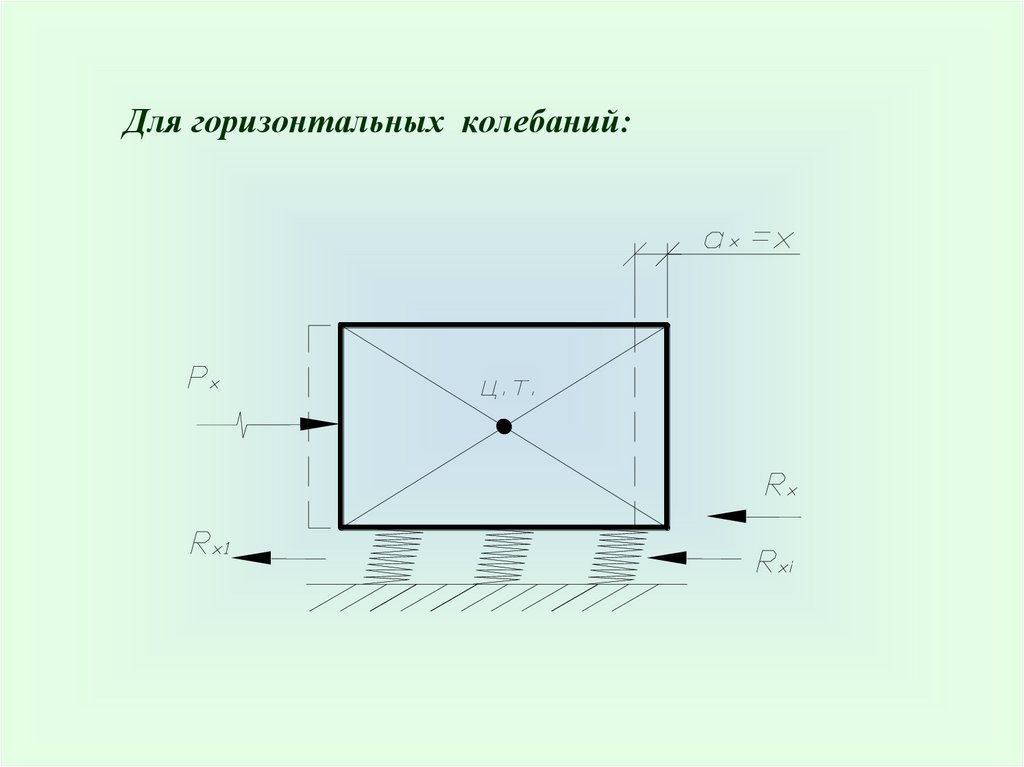
Для горизонтальных колебаний:45.
R х –горизонтальная реакция всех опор (пружин)Rх Rхi K х х,
K х C х А,
где Kх – общая жесткость основания при сдвиге;
Сх – жесткость условных пружин при сдвиге, распределенная по площади А или коэффициент
упругого равномерного сдвига.
46.
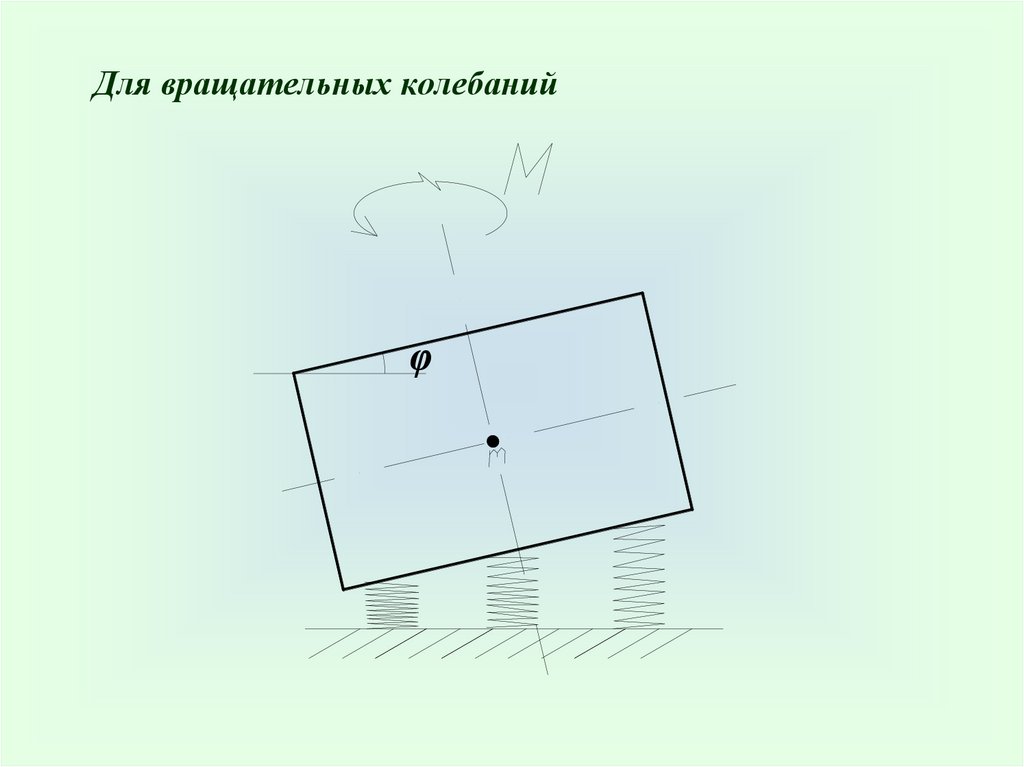
Для вращательных колебанийφ
47.
М – моментная реакция всех опор (пружин)М М i K ,
K C I ,
где Kφ – общая жесткость (вращательная) основания
при неравномерном сжатии;
Сφ – коэффициент упругого неравномерного сжатия;
I
– момент инерции фундамента.
48.
kz cCz
,
А
kx c
Cx
,
А
k c
C
,
А
Е
с
,
2
1
где kz, kx, kφ – коэффициенты, зависящие от соотношения размеров и формы фундамента.
49.
Связь между коэффициентами Сz, Сx, Сφ:С х 0,7 С z ;
C 2,0 C z .
50.
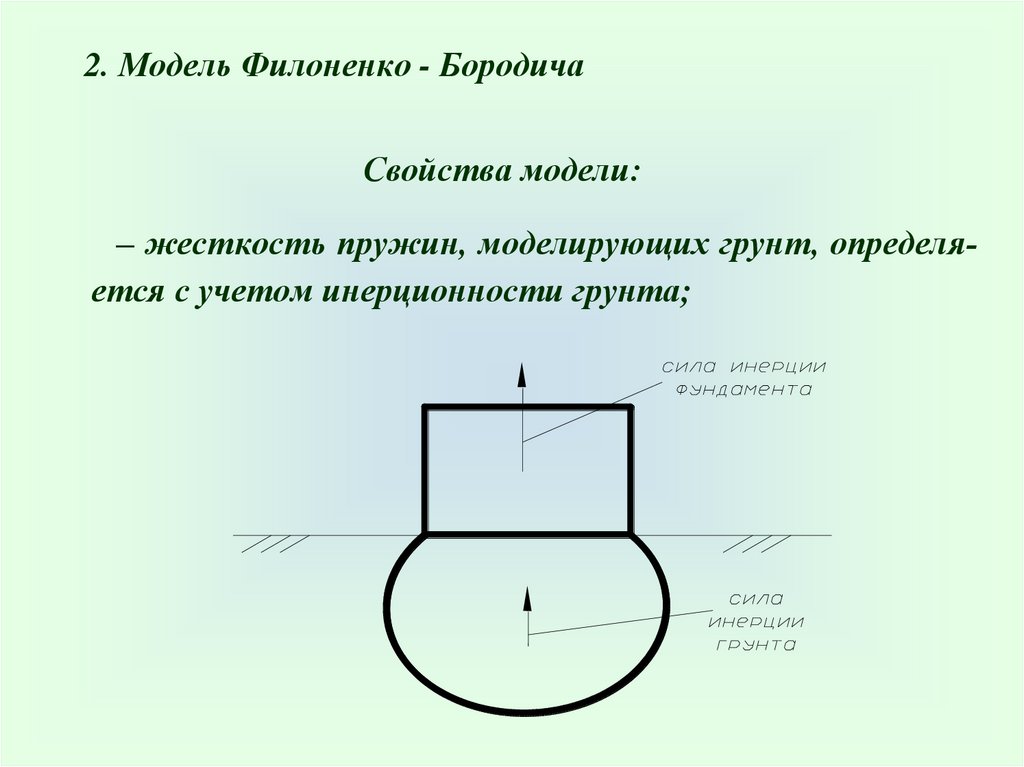
2. Модель Филоненко - БородичаСвойства модели:
– жесткость пружин, моделирующих грунт, определяется с учетом инерционности грунта;
51.
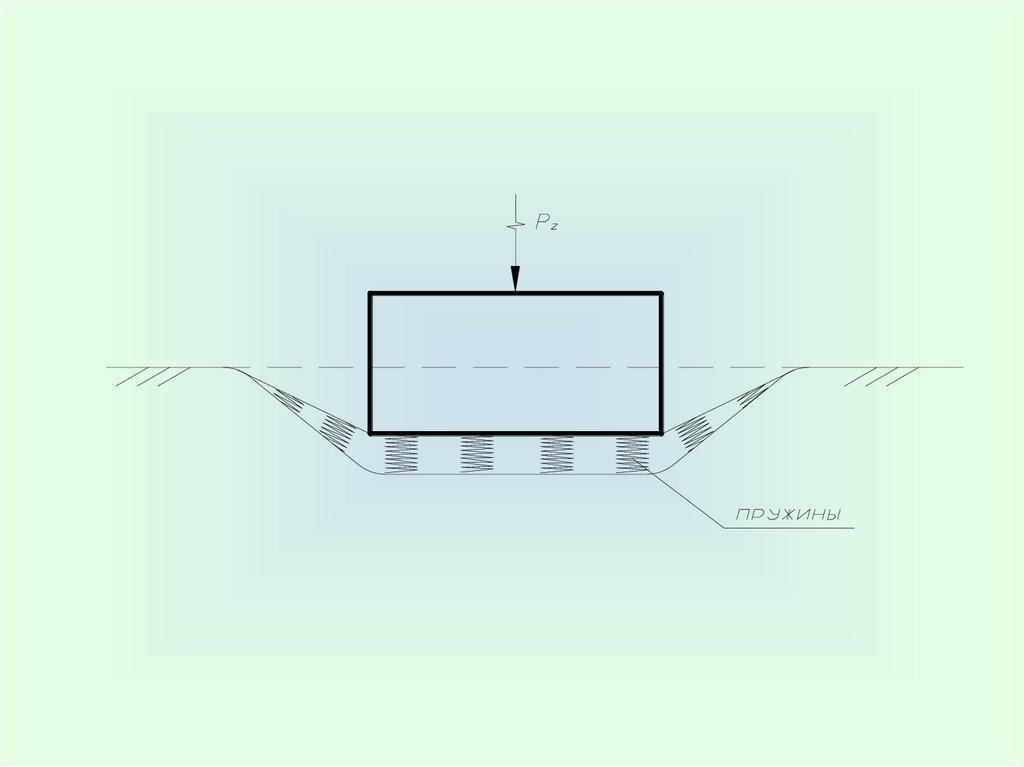
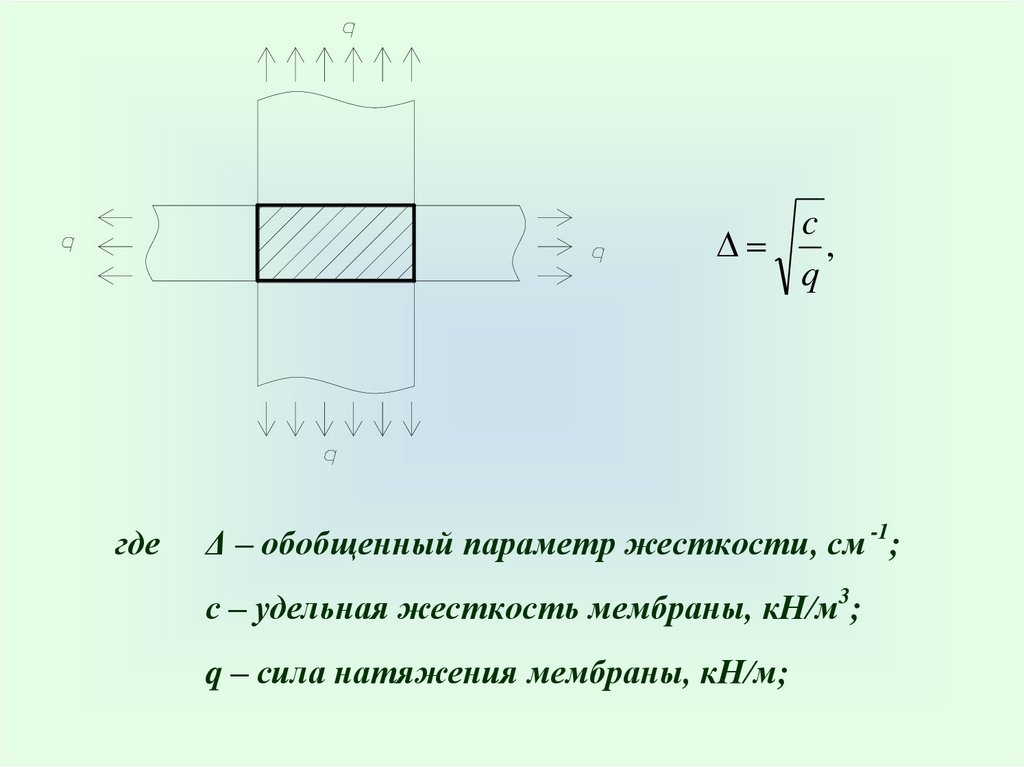
– модель основания принята в виде Винклеровской, накоторую дополнительно наложена мембрана, вовлекающая в работу грунт, находящийся за контурами подошвы фундамента.
52.
53.
c,
q
где
Δ – обобщенный параметр жесткости, см -1;
с – удельная жесткость мембраны, кН/м3;
q – сила натяжения мембраны, кН/м;
54.
Жесткость пружин (основания):K z C z А,
K x C x А,
K C I ,
55.
где:2 a b P
C z C0 1
,
А P0
2 a b P
C x D0 1
,
А P0
2 a 3 b P
C C0 1
,
А P0
56.
где:E
3
C0 17
,
кН
/
м
,
2
1
E
D0 17
, кН / м 3 ,
1 1 0,5
57.
Р– давление под подошвой фундамента;
Р0
– эталонное давление, равное 100 кПа;
а, b
– размеры подошвы фундамента;
Е
– модуль деформации;
ν
– коэффициент Пуассона.
Эта модель наиболее точно отражает реальные свойства грунтового основания.
58.
3. Модель упругого полупространстваСвойства модели:
– деформации вполне упруги, линейносвязаны с напряжениями и полностью исчезают после снятия динамической нагрузки;
59.
– материал основания однородный, сплошной, в немневозможны деформации разрывного характера;
60.
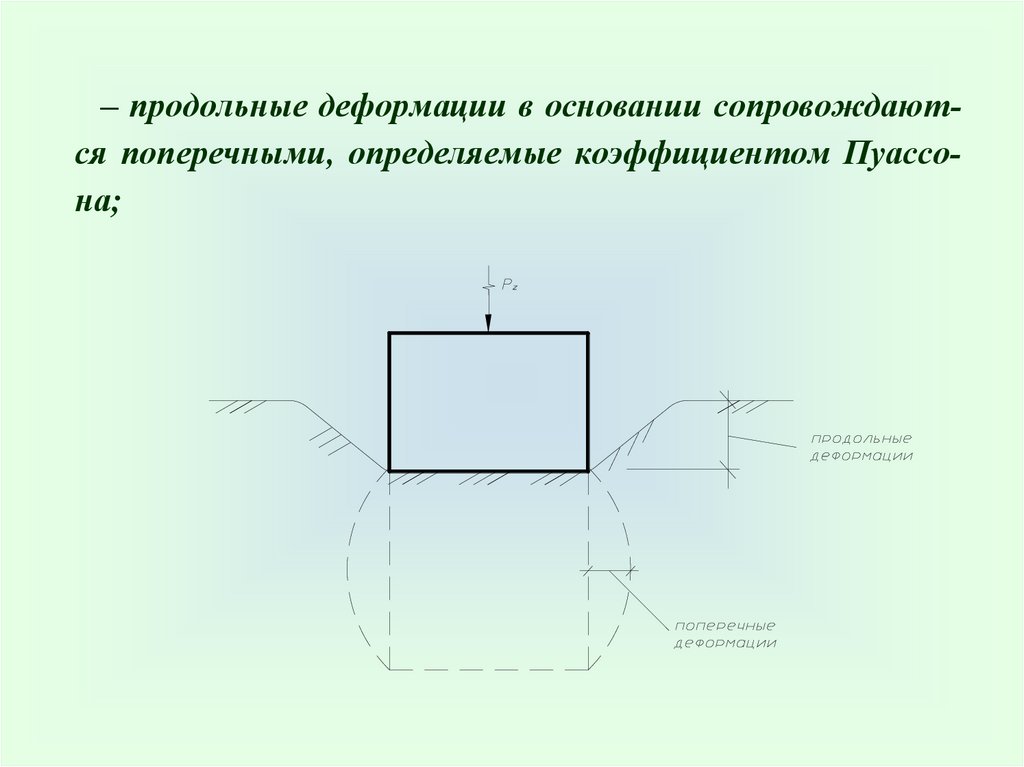
– продольные деформации в основании сопровождаются поперечными, определяемые коэффициентом Пуассона;61.
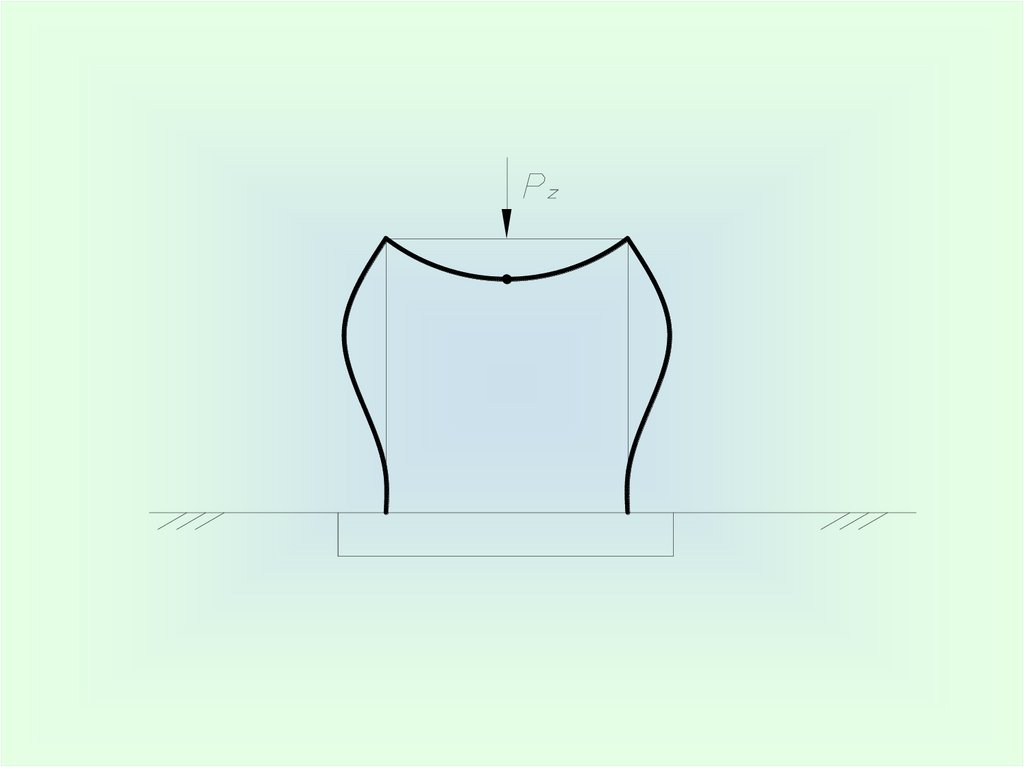
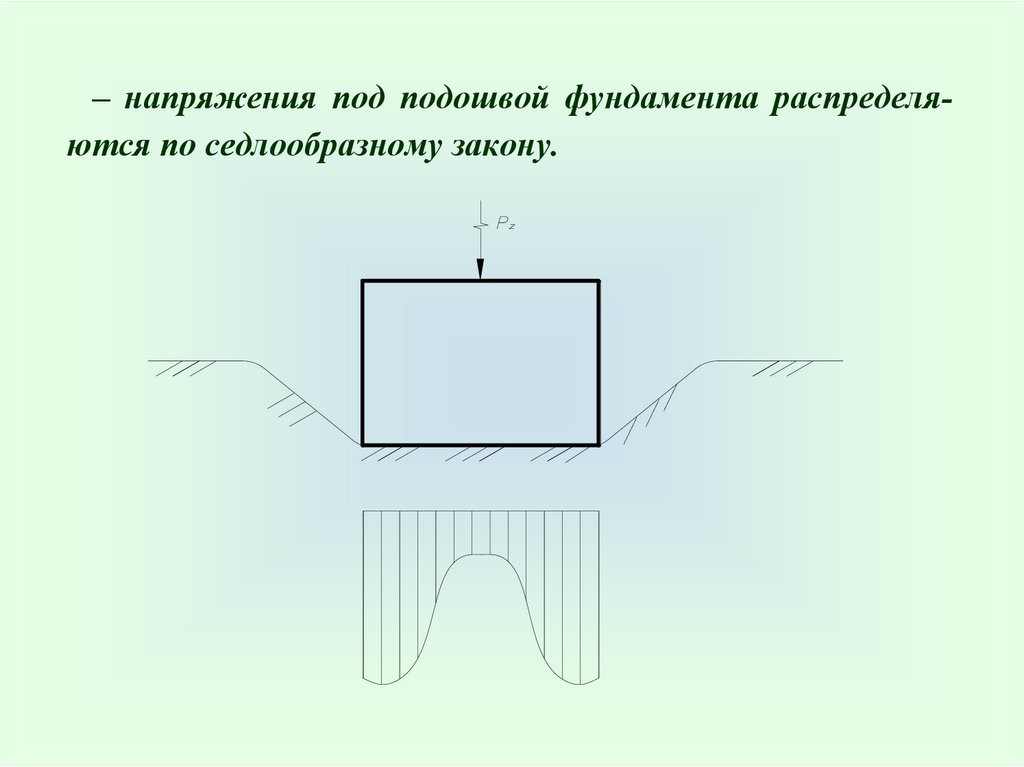
– напряжения под подошвой фундамента распределяются по седлообразному закону.62.
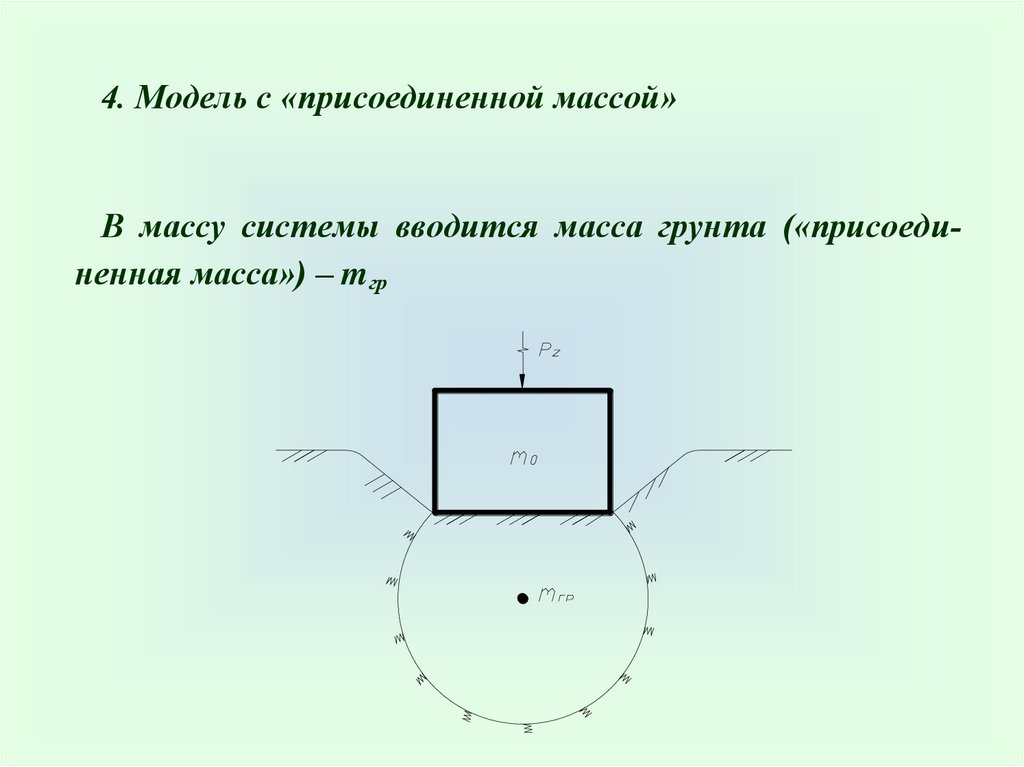
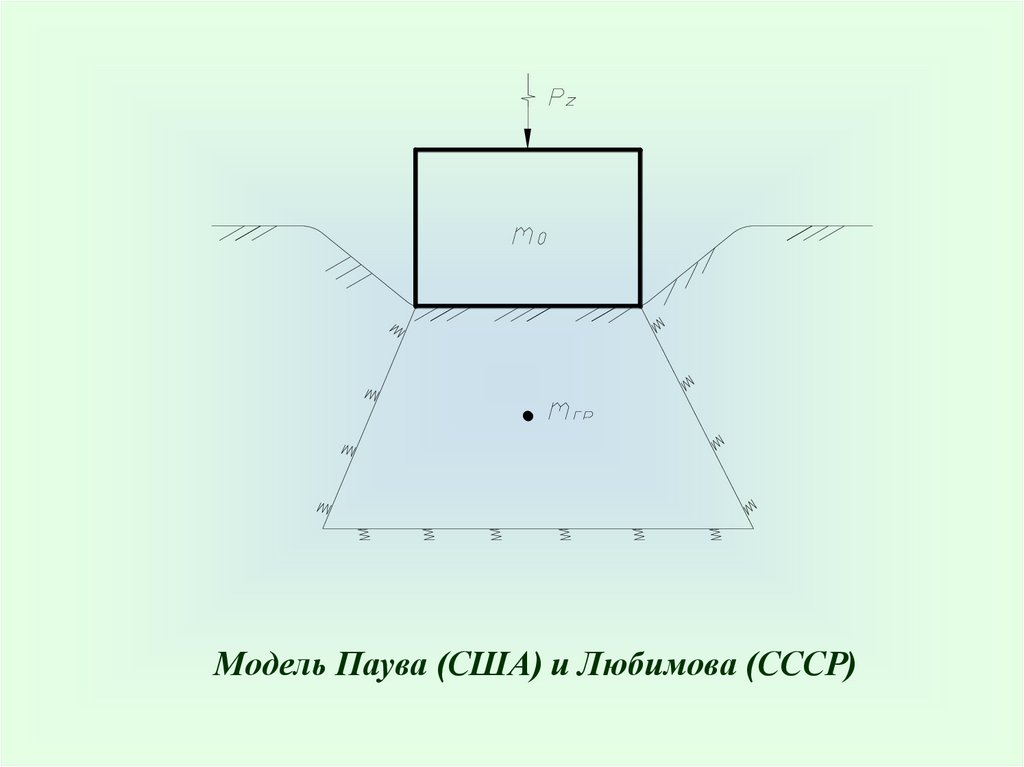
4. Модель с «присоединенной массой»В массу системы вводится масса грунта («присоединенная масса») – mгр
63.
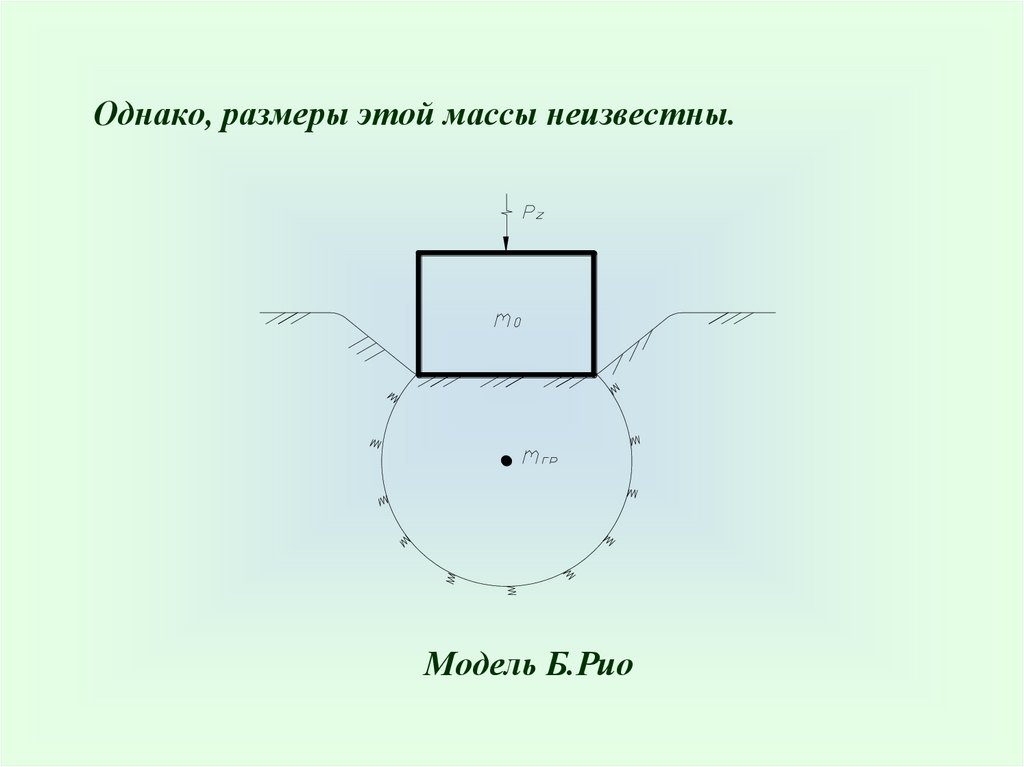
Однако, размеры этой массы неизвестны.Модель Б.Рио
64.
Модель Паува (США) и Любимова (СССР)65.
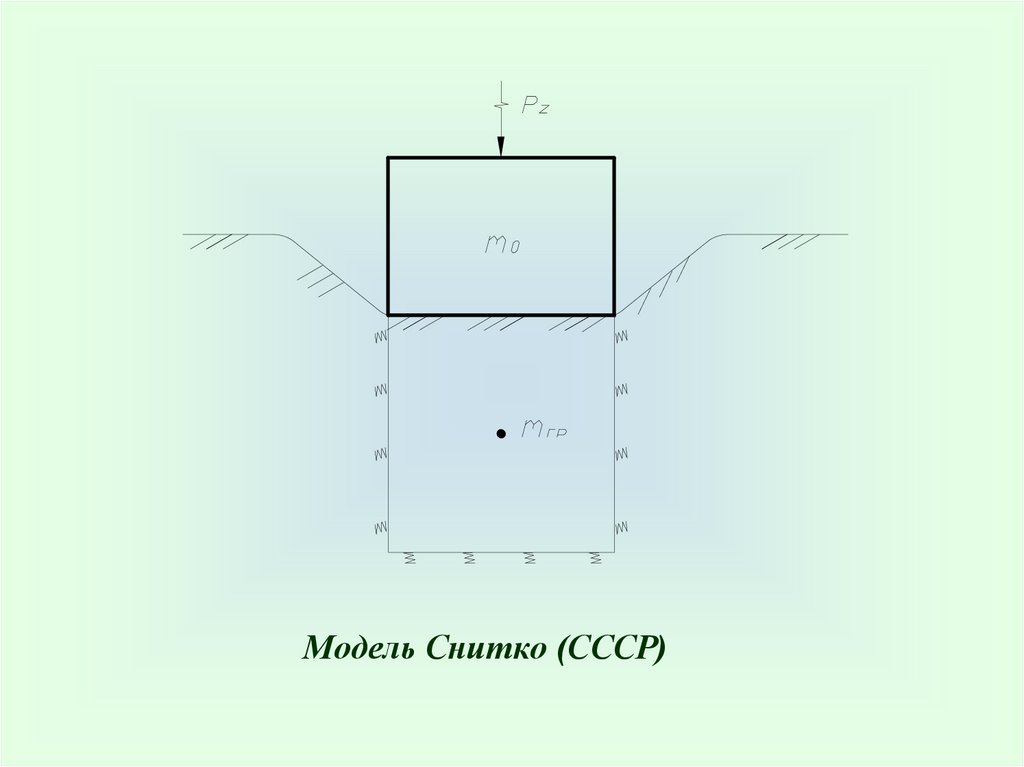
Модель Снитко (СССР)66.
Точность определения амплитуд колебаний по различным моделям зависит от правильности выбора той илииной модели.
67.
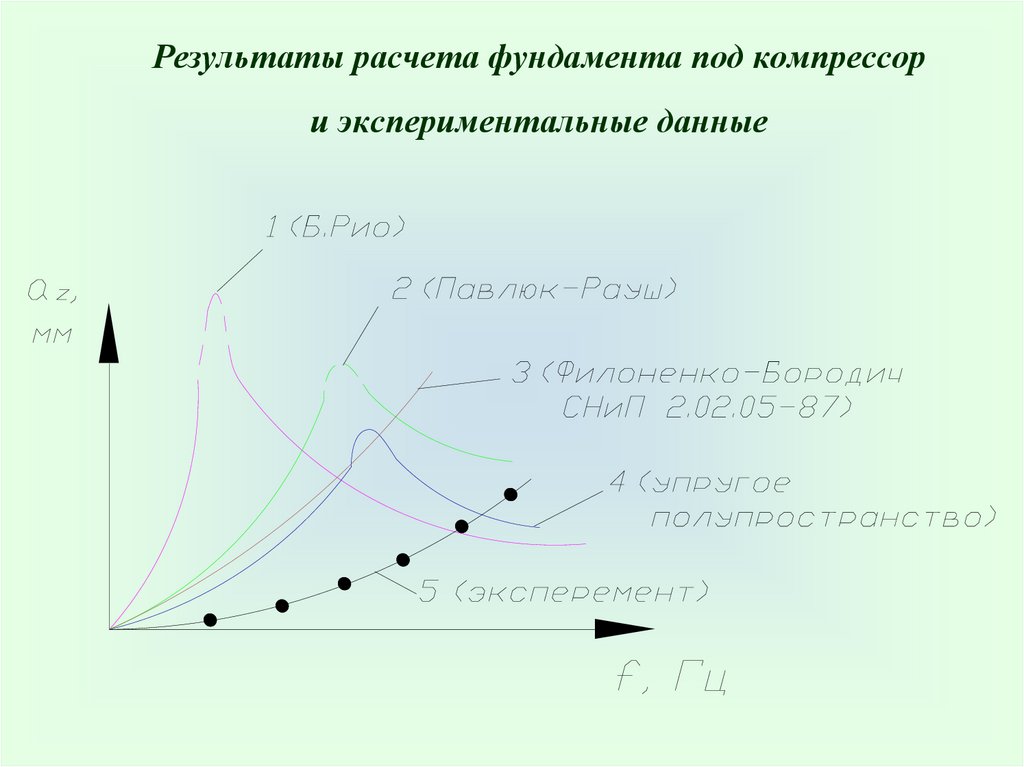
Результаты расчета фундамента под компрессори экспериментальные данные
68.
Вывод: проблема расчета фундаментов под машины сдинамическими нагрузками до сих пор решена
не полностью.
69.
Вывод и решениедифференциального уравнения
вертикальных колебаний
фундамента
70.
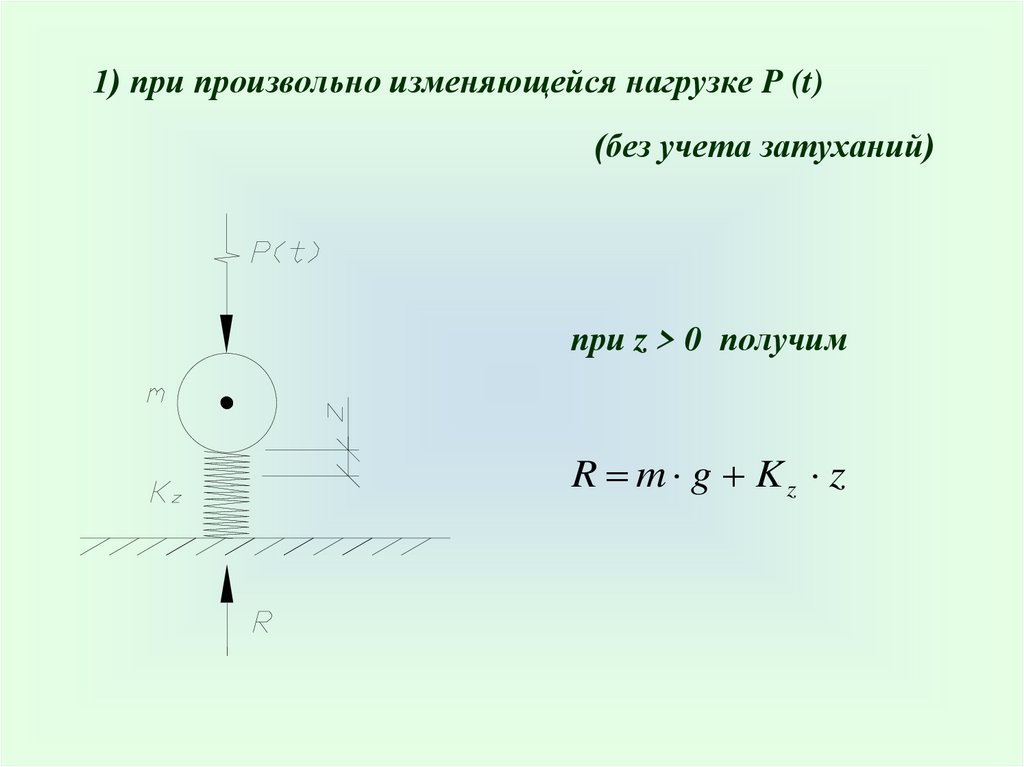
1) при произвольно изменяющейся нагрузке P (t)(без учета затуханий)
при z > 0 получим
R m g Kz z
71.
Для составления уравнения движения используетсяпринцип Даламбера:
«Уравнение движения может быть получено как уравнение движения в статике, если к внешним силам, действующих на систему, добавить силу инерции с обратным знаком по отношению направления движения».
72.
Q P(t ) m z // R,m z // Q P(t ) R 0,
т.к R m g K z z
m z Q P(t ) m g K z z 0,
//
m z // K z z P(t ),
73.
KzP(t)
z
z
,
m
m
//
2z
2 Kz
z
m
P(t)
z z
.
m
//
2
z
74.
2) при нагрузке P (t) = 0(свободные колебания)
z z 0
//
2
z
Решение данного уравнения:
z A sin z t B cos z t ,
где А и В – произвольные коэффициенты (получены из
начальных условий).
75.
при t = 0, z = 00 0 В 1
В 0
при t = 0, z / = v0ф
z / A z cos z t В z sin z t
A
z/
z
v0ф
z
az ,
76.
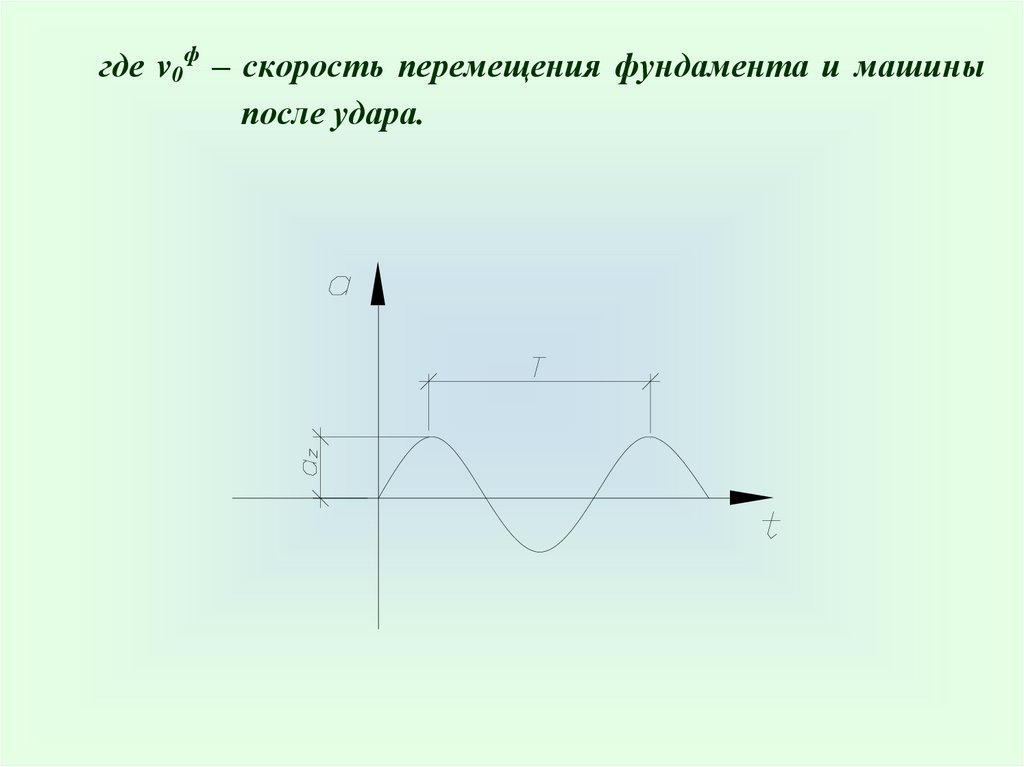
где v0ф – скорость перемещения фундамента и машиныпосле удара.
77.
1 m0 v0v
ф
0
m0 m
1 m0 v0
az
,
m0 m z
так как m0 m,
1 m0 v0
a
,
z
m z
(используется при расчете фундамента под молот)
78.
где m0 – масса ударной части;m – масса фундамента и машины;
v0 – скорость ударной части в момент соударения;
ε
– коэффициент восстановления удара;
λz – частота свободных (собственных) колебаний.
79.
3) при нагрузке P (t) = Pz · sin(ω · t) – гармоническиеколебания
здесь ω – частота динамического воздействия
(вынужденных колебаний);
t
– время (переменная).
Pz sin t
z z
m
//
2
z
Решение данного уравнения:
z аz sin t ,
z / аz cos t ,
z // аz sin t 2 .
80.
а z sin t а z sin t2
2
z
Pz sin t
m
Pz
аz ,
m
2
z
2
Pz
Pz
1
аz
2
2
2
2
m z
m z
1 2
z
,
81.
11 2
z
2
Pz
аz
аст ,
Kz
где η – коэффициент динамичности системы.
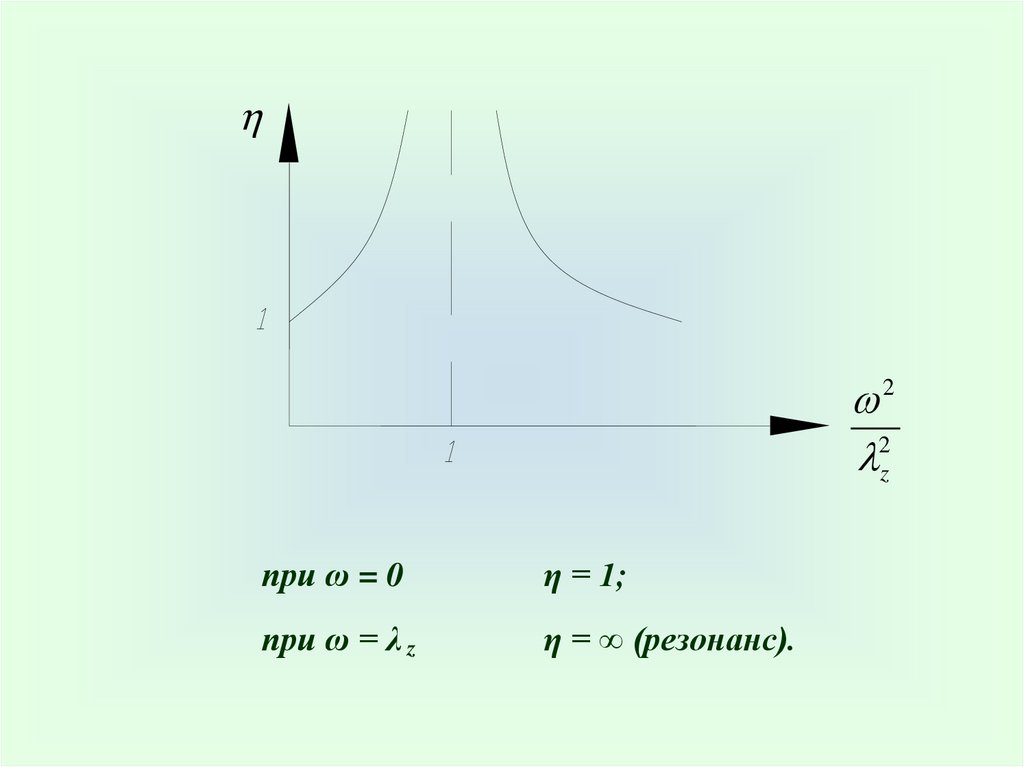
82.
22z
при ω = 0
η = 1;
при ω = λ z
η = ∞ (резонанс).
83.
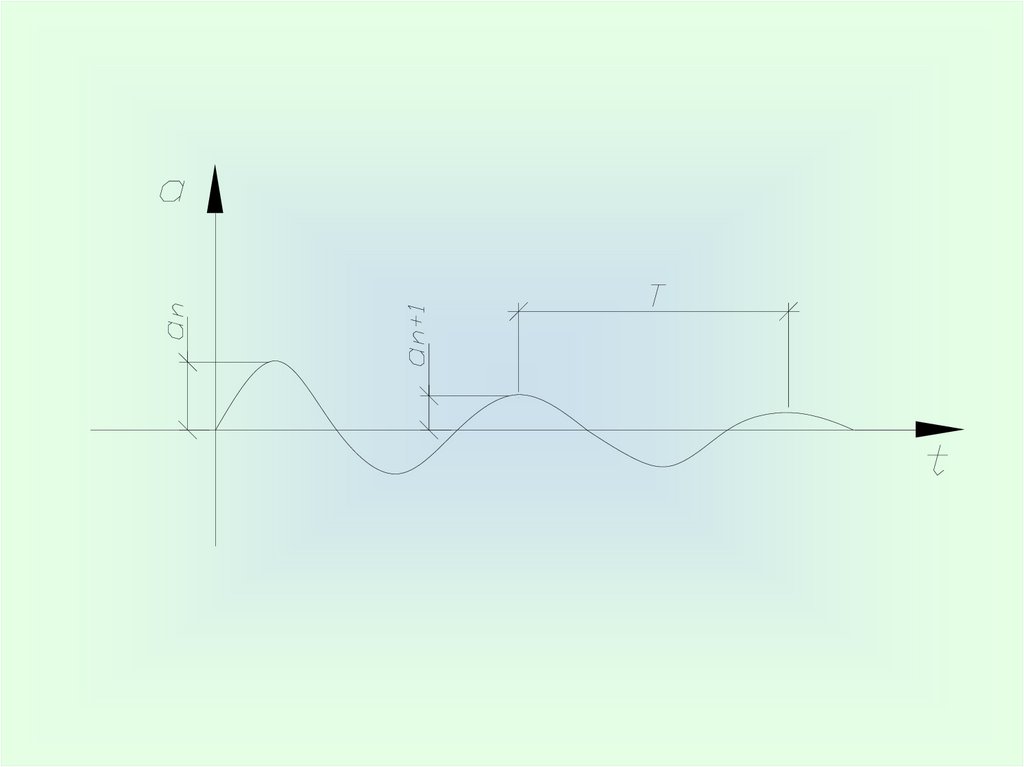
С учетом затуханий:az
Pz
1
аст ,
2
Kz 2
1 2 Ф 2
z
2
Ф
,
z
an
,
ln
an 1
где Ф
δ
– модуль затухания;
– логарифмический декремент затухания.
84.
85.
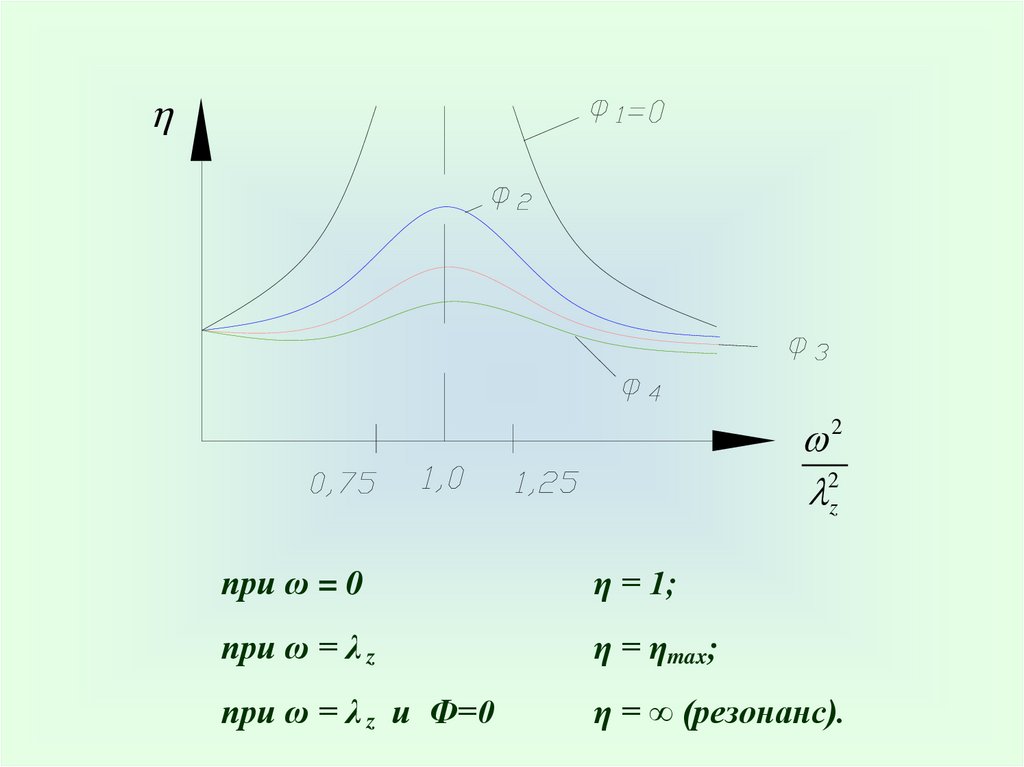
22z
при ω = 0
η = 1;
при ω = λ z
η = ηmax;
при ω = λ z и Ф=0
η = ∞ (резонанс).






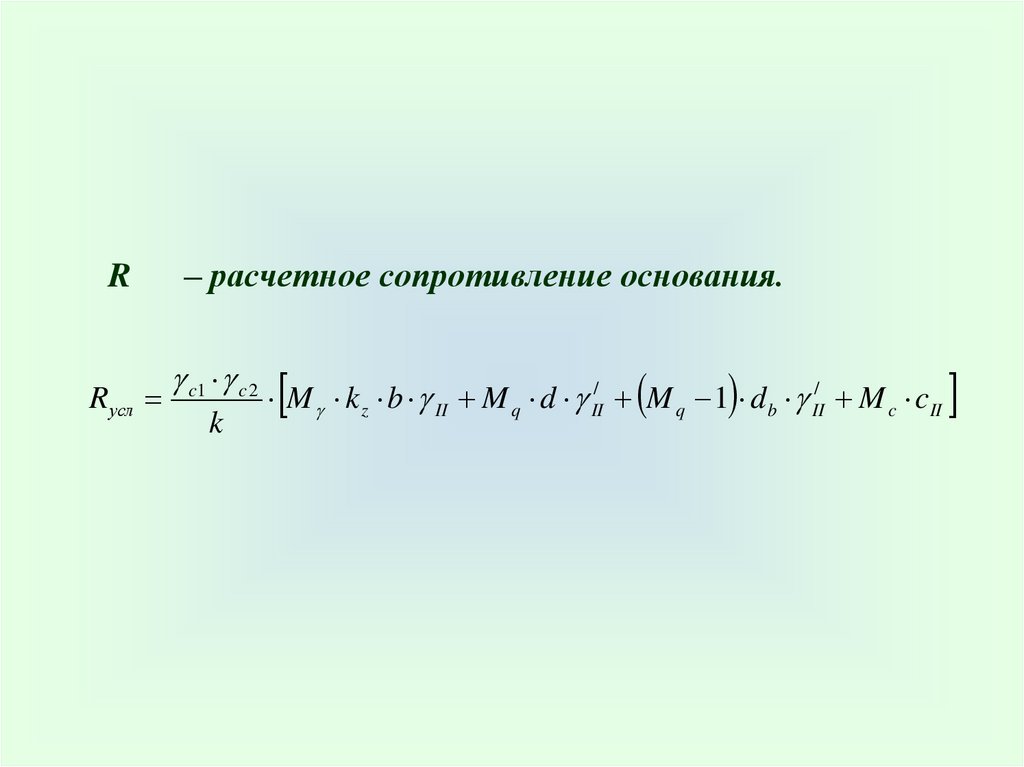

















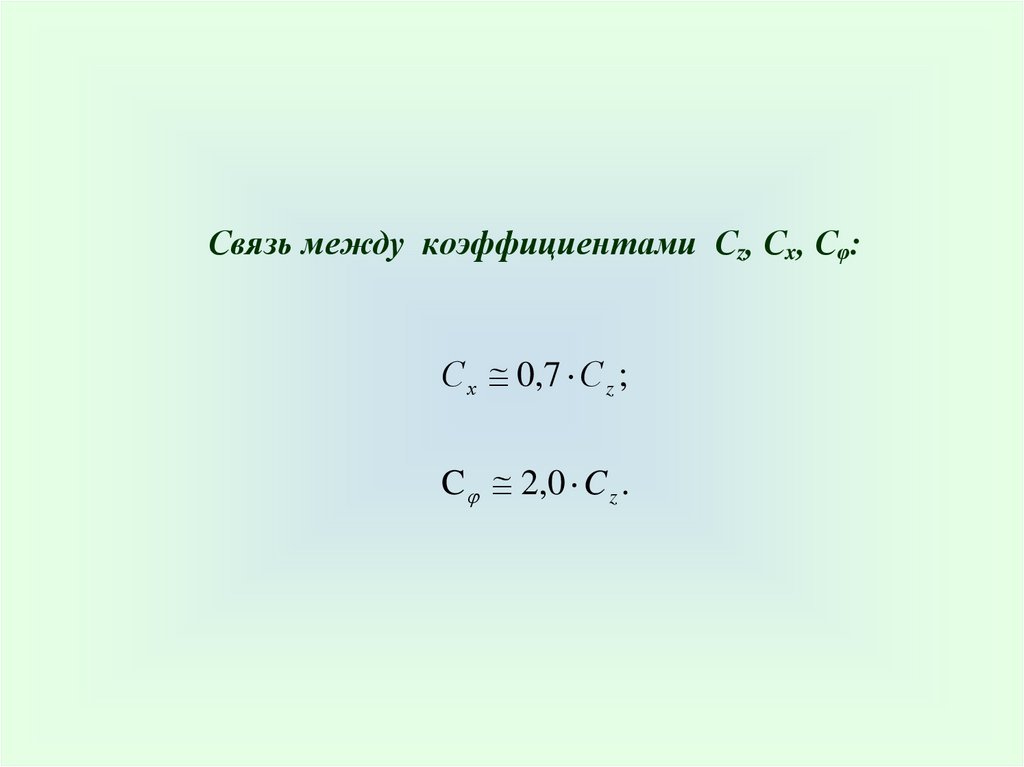


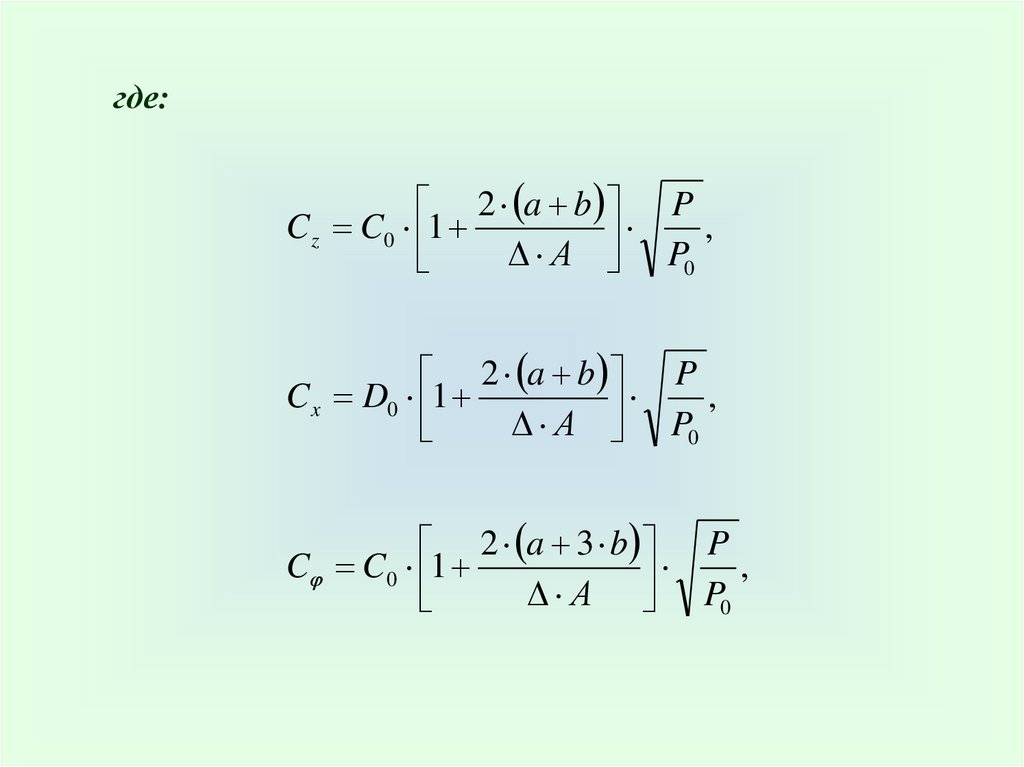
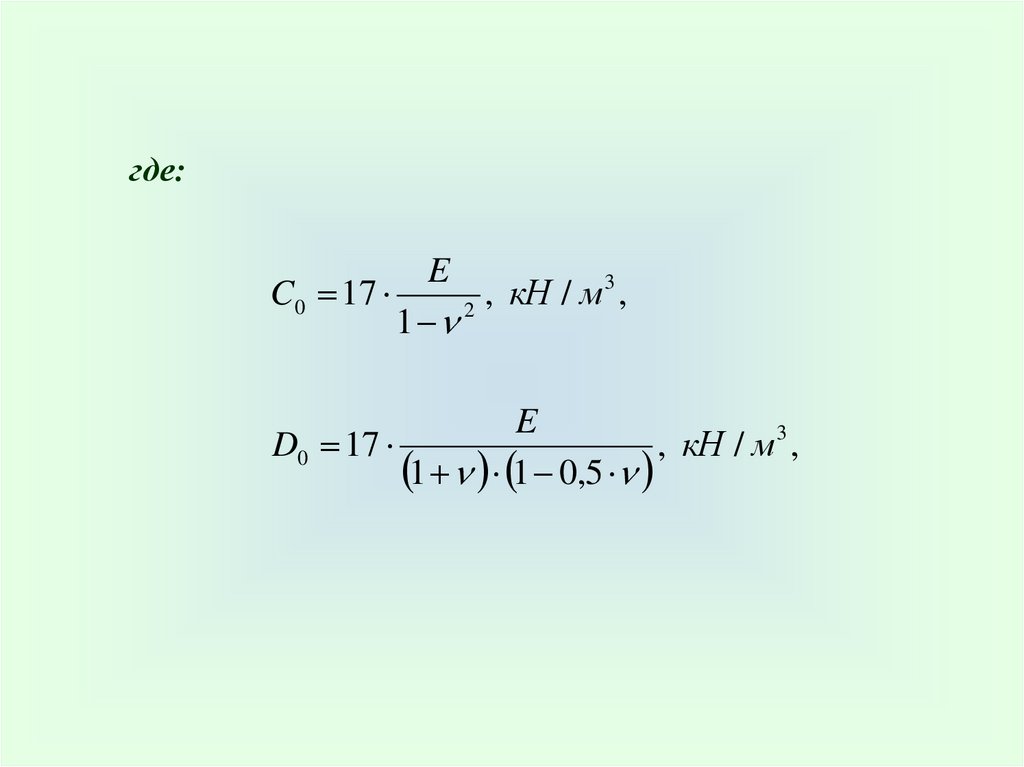






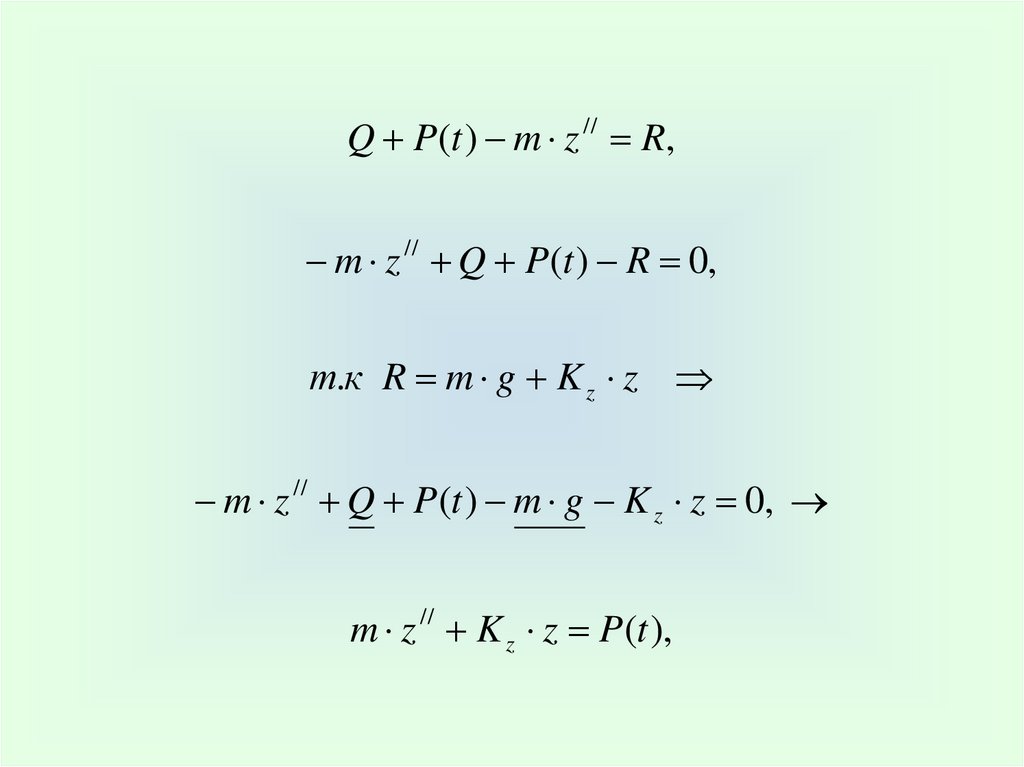
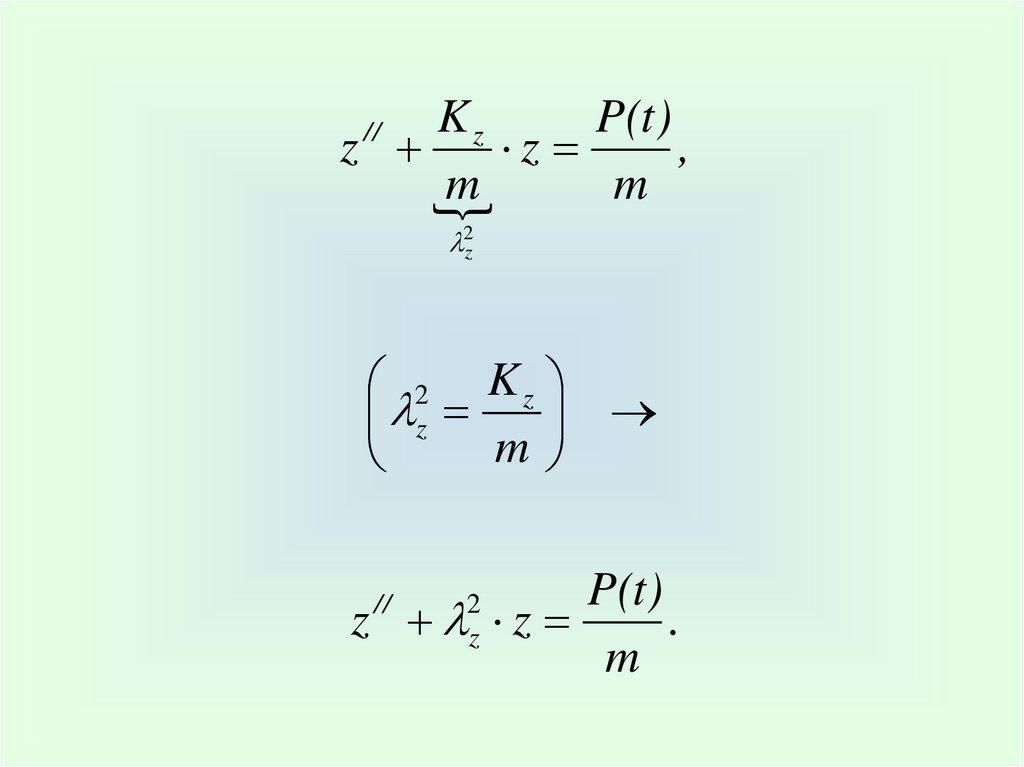

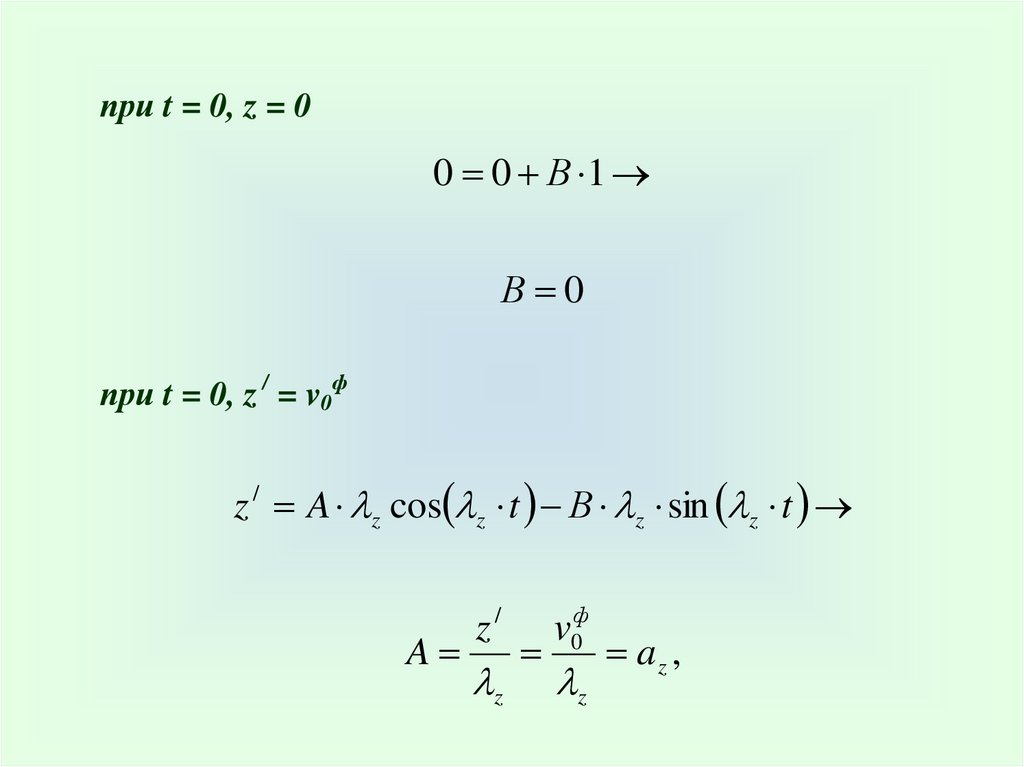



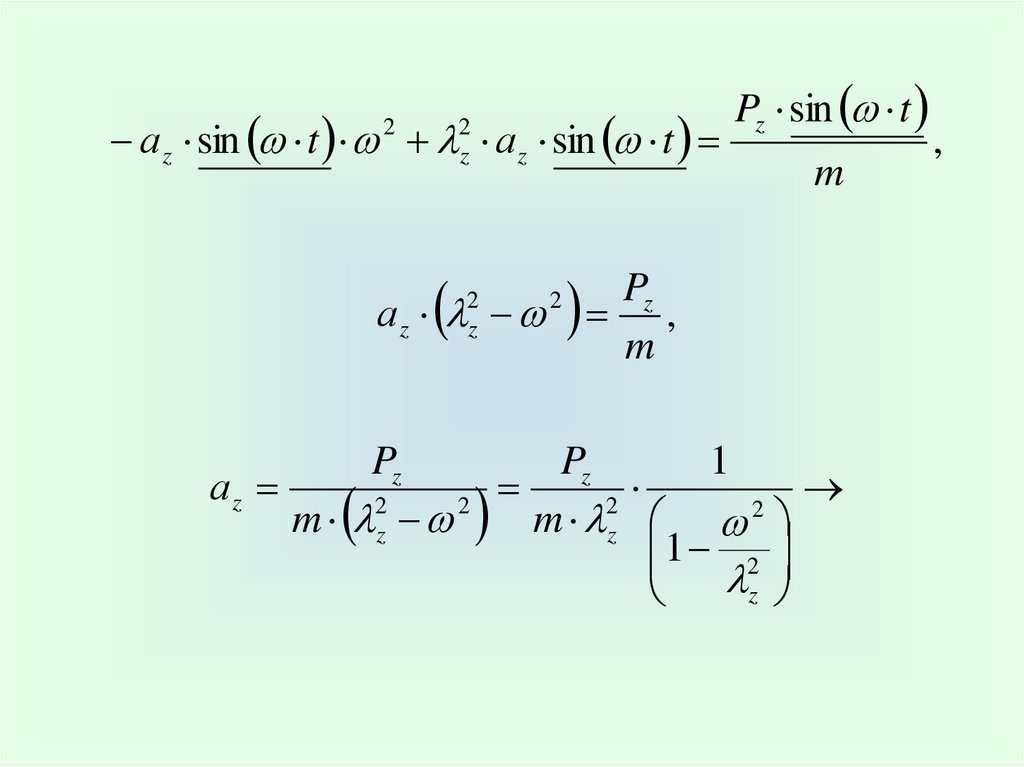


 Промышленность
Промышленность








