Лекция 2 ТПР

1.

Филиал ФГБОУ ВО
«Национальный исследовательский университет «МЭИ» в г. Смоленске
Теория принятия решений
Доцент кафедры ВТ
кандидат технических наук, доцент
И.А. Денисова
Смоленск
Смоленск
– 2024
2011

2.

Лекция № 2
Методы решения задач линейного
программирования

3.

УЧЕБНЫЕ ВОПРОСЫ
1. Общая характеристика методов решения задач линейного
программирования
2. Симплекс-метод решения
основной задачи линейного программирования
3. Венгерский метод решения
задачи линейного программирования о назначениях

4.

1 вопрос
Общая характеристика методов
решения задач линейного
программирования

5.

ОСНОВОПОЛАГАЮЩИЙ ПРИНЦИП ТПР
сформулировали
Моргенштерн:
американские
ученые
Нейман
и
Лицо, принимающее решение, должно всегда
выбирать альтернативу с максимально ожидаемой
полезностью, результатом.
5

6.

Задача, модель которой содержит только
линейные функции искомых переменных,
называется задачей линейного
программирования.
6

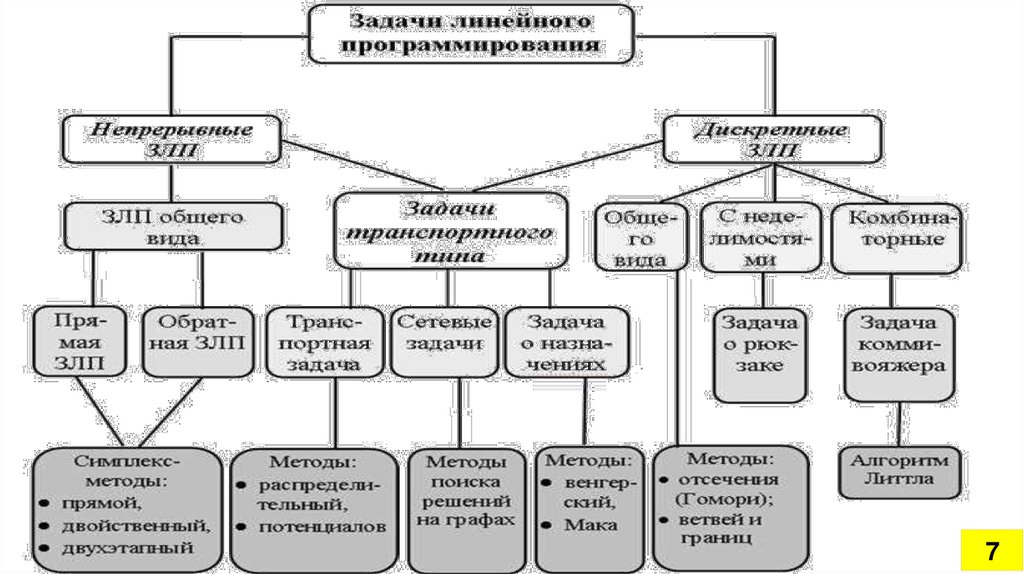
7.

7

8.

Формы записи ЗЛП
Каноническая форма
n
L C j x j max
j 1
Стандартная форма
n
L C j x j max/min
j 1
a11x1 a12 x2 ... a1n xn b1 ; a11 x1 a12 x2 ... a1n xn / b1 ;
a21x1 a22 x2 ... a2 n xn b2 ; a 21 x1 a 22 x2 ... a 2 n xn / b2 ;
a x a m 2 x2 ... a mn xn / bm ;
am1 x1 am 2 x2 ... amn xn bm ; m1 1
x j 0.
x j 0.
8

9.

2 вопрос
Симплекс-метод решения
основной задачи линейного
программирования

10.

Симплекс (лат. simplex - простой) –
простейший
выпуклый
многогранник
в n-мерном пространстве с n+1 вершиной
(например, тетраэдр в 3-мерном пространстве)
10

11.

Симплекс (лат. simplex - простой) – простейший выпуклый
многогранник в n-мерном пространстве с n+1 вершиной
(например, тетраэдр в 3-мерном пространстве)
Впервые симплексный
метод был предложен
американским ученым
Дж. Данцигом в 1949 г.
Джордж Бернард Данциг (1914-2005) –
американский математик, разработал симплексный
алгоритм, считается основоположником методов
линейного программирования
Идеи симплексного метода были
разработаны в 1939 г. российским
ученым Л.В.Канторовичем Леонид Витальевич Канторович (1912-1986) –
советский математик и экономист, лауреат
Нобелевской премии по экономике 1975 года «за
вклад в теорию оптимального распределения
ресурсов». Один из создателей линейного
программирования

12.

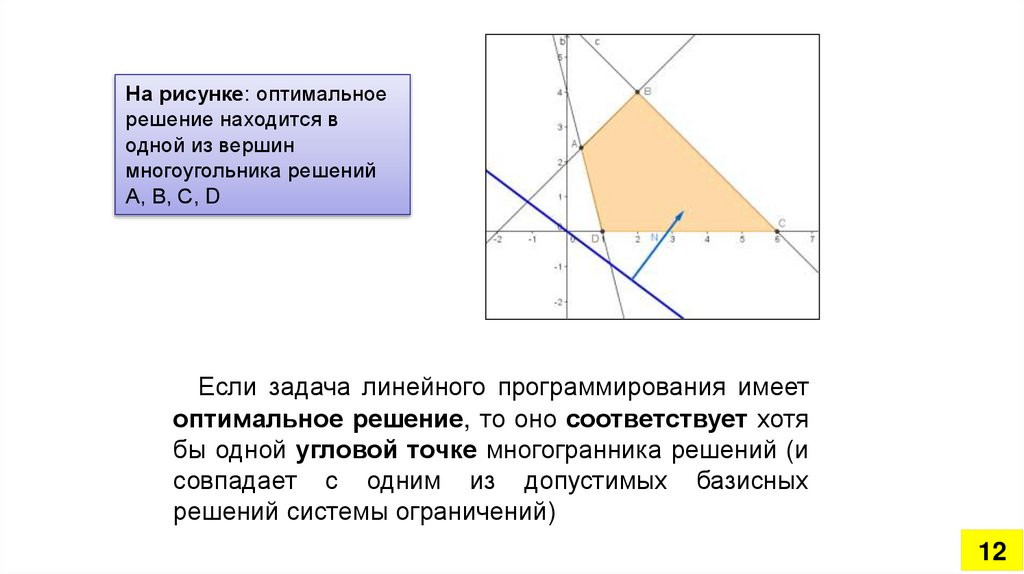
На рисунке: оптимальное
решение находится в
одной из вершин
многоугольника решений
А, В, С, D
Если задача линейного программирования имеет
оптимальное решение, то оно соответствует хотя
бы одной угловой точке многогранника решений (и
совпадает с одним из допустимых базисных
решений системы ограничений)
12

13.

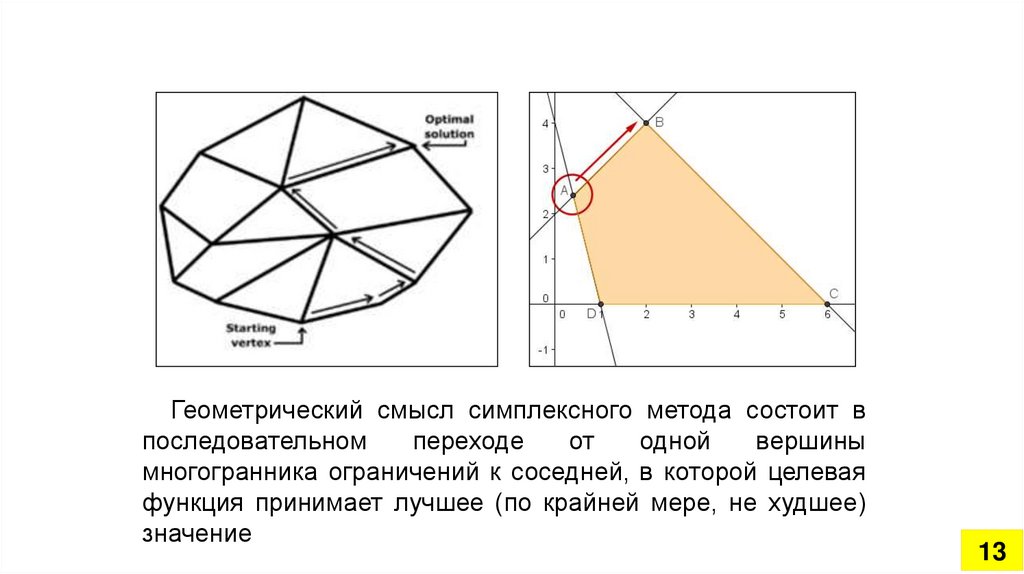
Геометрический смысл симплексного метода состоит в
последовательном
переходе
от
одной
вершины
многогранника ограничений к соседней, в которой целевая
функция принимает лучшее (по крайней мере, не худшее)
значение
13

14.

Симплекс-метод реализует направленный перебор допустимых
базисных решений в виде итеративного процесса.
На каждой итерации осуществляется переход по ребру допустимого
множества от одной вершины к другой, смежной исходной, в которой
значение критерия лучше или, в редких случаях, не хуже, чем в
исходной.
В симплекс-методе три основных этапа:
1) построение начального базисного решения;
2) процедура перехода от одного базисного
решения к другому;
3) проверка оптимальности.
14

15.

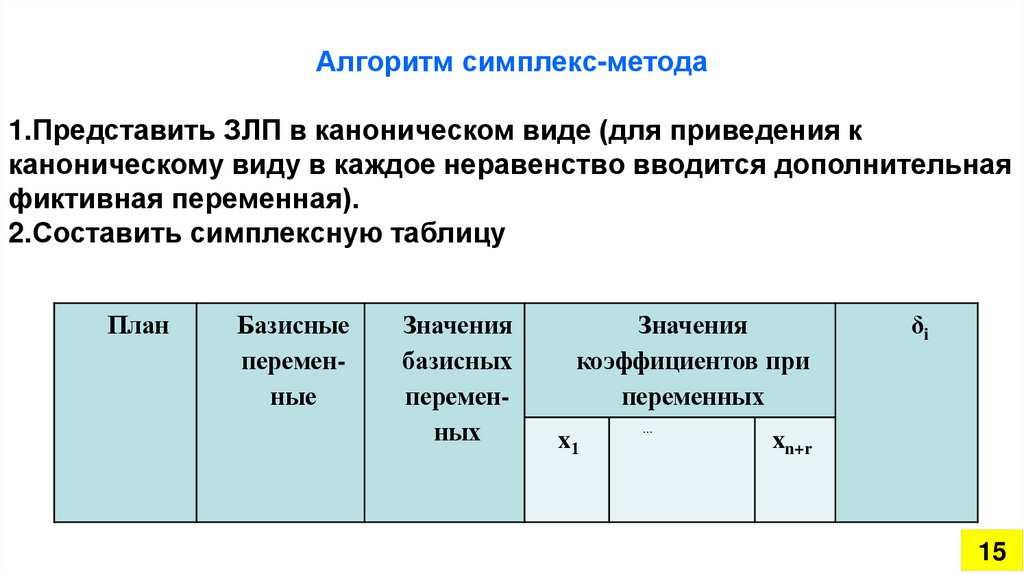
Алгоритм симплекс-метода
1.Представить ЗЛП в каноническом виде (для приведения к
каноническому виду в каждое неравенство вводится дополнительная
фиктивная переменная).
2.Составить симплексную таблицу
План
Базисные
переменные
Значения
базисных
переменных
Значения
коэффициентов при
переменных
x1
…
δi
xn+r
15

16.

Алгоритм симплекс-метода
3. Составить начальный опорный план (заполнить таблицу):
базисные переменные ← фиктивные переменные;
значения базисных переменных ← правые части уравнений системы
ограничений;
значения коэффициентов при переменных ← коэффициенты при
переменных левых частей уравнений системы ограничений;
индексная строка ← коэффициенты при переменных критерия (если
ЗЛП на max, то выписывать с обратным знаком).
4. Определить разрешающий элемент (РЭ):
среди элементов индексной строки выбрать min (ведущий столбец);
рассчитать δi=значение базисной переменной/ элемент ведущего
столбца;
выбрать РЭ из строки, соответствующей min(δi).
16

17.

Алгоритм симплекс-метода
5. Заполнение следующего плана симплексной таблицы:
в список базисных переменных войдет переменная с
номером=второму индексу РЭ;
соответствующая строка пересчитывается путем деления на РЭ;
прочие элементы нового плана пересчитываются по формуле
НЭ=СтЭ-(А*В)/РЭ, где А и В – вершины «прямоугольника»,
образованного РЭ и СтЭ.
6. Проверка плана симплексной таблицы на оптимальность:
если все элементов индексной строки ≥0, то конец решения и шаг 7,
иначе - шаг 4.
7. Ответ ЗЛП:
Х opt =(значения базисных переменных и 0);
opt = элемент индексной строки и столбца значений базисных
переменных.
17

18.

Пример решения задачи ЛП
L=3x1+5x2+4x3→max
0,1x1+0,2x2+0,4x3 1100
0,05x1+0,02x2+0,02x3 120
3x1+x2+2x3 8000
x1 0
x2 0
x3 0
L=3x1+5x2+4x3→max
0,1x1+0,2x2+0,4x3+x4=1100
0,05x1+0,02x2+0,02x3+x5=120
3x1+x2+2x3+x6=8000
x1 0
x2 0
x3 0
x4 0
x5 0
x6 0
18

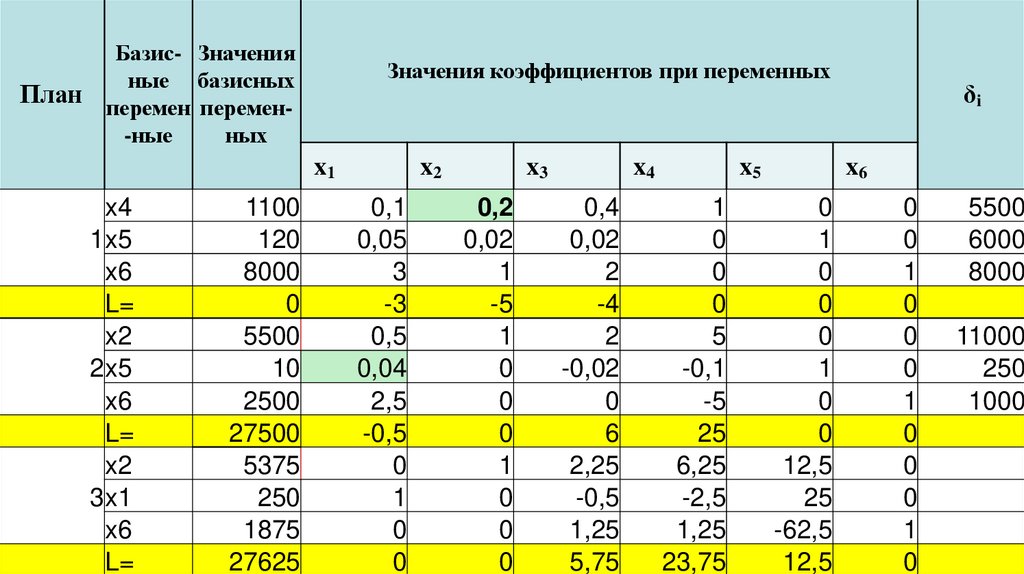
19.

План
Базис- Значения
ные базисных
перемен перемен-ные
ных
Значения коэффициентов при переменных
x1
x4
1x5
x6
L=
x2
2x5
x6
L=
x2
3x1
x6
L=
1100
120
8000
0
5500
10
2500
27500
5375
250
1875
27625
x2
0,1
0,05
3
-3
0,5
0,04
2,5
-0,5
0
1
0
0
x3
0,2
0,02
1
-5
1
0
0
0
1
0
0
0
x4
0,4
0,02
2
-4
2
-0,02
0
6
2,25
-0,5
1,25
5,75
x5
1
0
0
0
5
-0,1
-5
25
6,25
-2,5
1,25
23,75
δi
x6
0
1
0
0
0
1
0
0
12,5
25
-62,5
12,5
0
0
1
0
0
0
1
0
0
0
1
0
5500
6000
8000
11000
250
1000

20.

Пример решения задачи ЛП
Lmax= 27625
X1=250
X2=5375
x3 =0
X4=0
X5=0
x6 =1875
20

21.

В MS Excel для решения задачи
линейного программирования используется
надстройка ПОИСК РЕШЕНИЯ.
21

22.

Решим в MS Excel задачу линейного программирования
1. Создадим область переменных
Ячейки В2:В6 будут играть
роль переменных
(пока они пусты)
22

23.

Решим в MS Excel задачу линейного программирования
2. Введем формулу вычисления значений
целевой функции
Например, в ячейку А8
23

24.

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
В ячейках В11:В13 введем
правые части ограничений
системы
24

25.

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Первое ограничение
25

26.

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Второе ограничение

27.

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем
вычислять левые части
ограничений в системе
Третье ограничение
27

28.

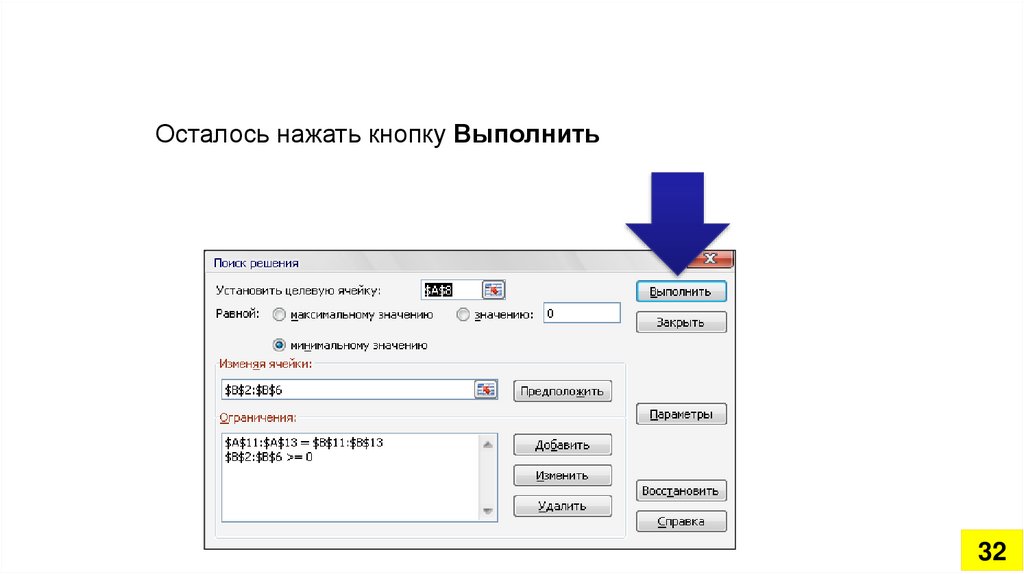
Решим в MS Excel задачу линейного программирования
4. Вызовем окно диалога Поиск решения
При этом удобно,
если активной
ячейкой является
ячейка со
значением
целевой функции
28

29.

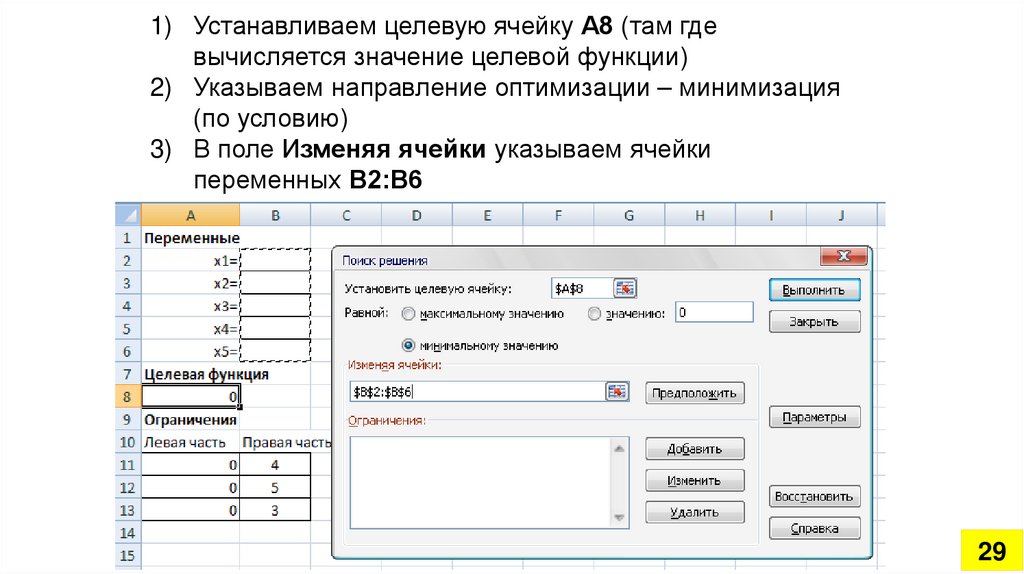
1) Устанавливаем целевую ячейку А8 (там где
вычисляется значение целевой функции)
2) Указываем направление оптимизации – минимизация
(по условию)
3) В поле Изменяя ячейки указываем ячейки
переменных В2:В6
29

30.

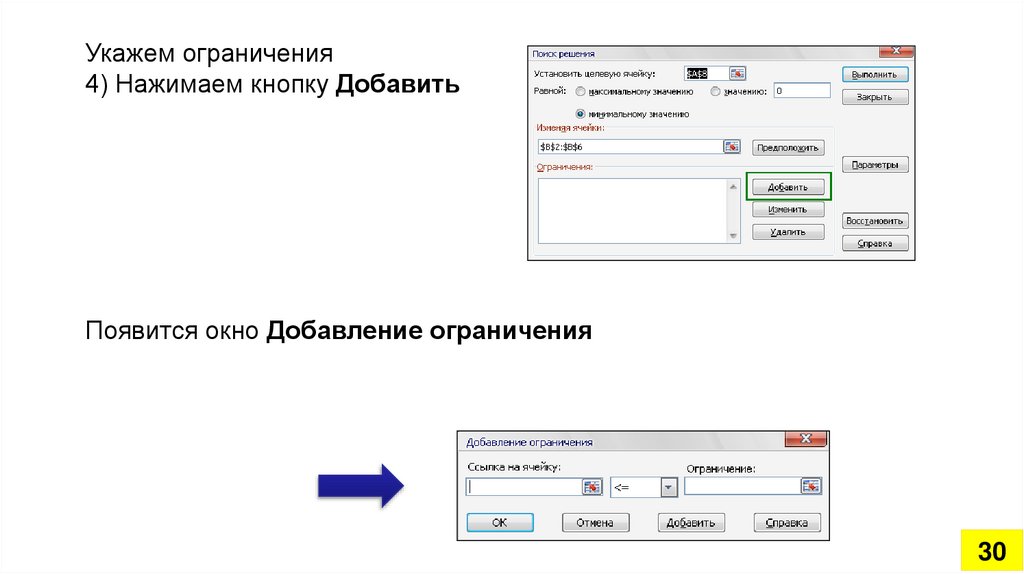
Укажем ограничения
4) Нажимаем кнопку Добавить
Появится окно Добавление ограничения
30

31.

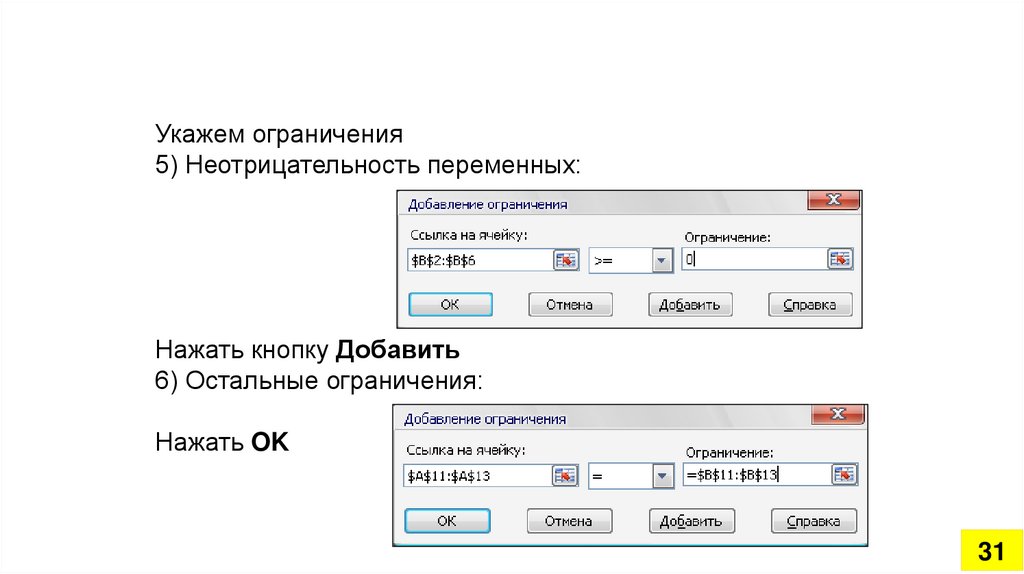
Укажем ограничения
5) Неотрицательность переменных:
Нажать кнопку Добавить
6) Остальные ограничения:
Нажать OK
31

32.

Осталось нажать кнопку Выполнить
32

33.

Результаты
Ответ:
33

34.

3 вопрос
Венгерский метод решения
задачи о назначениях линейного
программирования

35.

Алгоритм решения задачи о назначениях
(Венгерский алгоритм )
Шаг 1. Редукция строк /столбцов матрицы:
в каждой строке определить min элемент и вычесть его из каждого элемента своей
строки;
в каждом столбце определить min элемент и вычесть его из каждого элемента
своего столбца.
Выполнить распределение. Если распределение успешно, то – решение получено,
иначе – шаг 2 алгоритма.
Шаг 2.
Подсчитать количество «0» в строках и «вычеркнуть» строку с max количеством
«0»;
подсчитать количество «0» в столбцах и «вычеркнуть» столбец с max количеством
«0»;
продолжать, чередуя строки/столбцы, пока все «0» не окажутся «вычеркнутыми».
Среди «невычеркнутых» элементов выбрать min и вычесть его значение из
каждого «невычеркнутого» элемента и прибавить его значение к каждому «дважды
вычеркнутому» элементу.
Выполнить распределение. Если распределение успешно, то - решение получено,
иначе – повторить шаг 2 алгоритма.
35

36.

Модель задачи о назначениях (n=m=4)
Найти
при
Пример задачи о назначениях
36

37.

Пример задачи о назначениях
Минимальное значение целевой функции =10.
37

38.

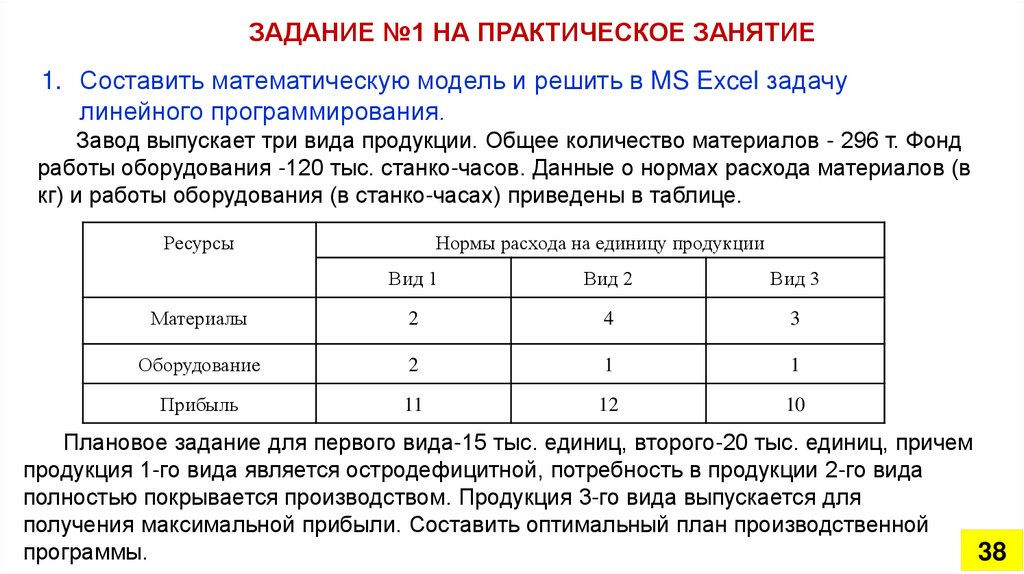
ЗАДАНИЕ №1 НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Составить математическую модель и решить в MS Excel задачу
линейного программирования.
Завод выпускает три вида продукции. Общее количество материалов - 296 т. Фонд
работы оборудования -120 тыс. станко-часов. Данные о нормах расхода материалов (в
кг) и работы оборудования (в станко-часах) приведены в таблице.
Ресурсы
Нормы расхода на единицу продукции
Вид 1
Вид 2
Вид 3
Материалы
2
4
3
Оборудование
2
1
1
Прибыль
11
12
10
Плановое задание для первого вида-15 тыс. единиц, второго-20 тыс. единиц, причем
продукция 1-го вида является остродефицитной, потребность в продукции 2-го вида
полностью покрывается производством. Продукция 3-го вида выпускается для
получения максимальной прибыли. Составить оптимальный план производственной
программы.
38

39.

ЗАДАНИЕ №2 НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Решить симплекс-методом задачу линейного программирования.
2. Решить в MS Excel задачу линейного программирования.
L=6x1+5x2 +5x3 →max
3x1+6x2+4x3 180
2x1+x2 +2x3 50
2x1+3x2+x3 40
x1 0
x2 0
x3 0
39

40.

ЗАДАНИЕ №3 НА ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
1. Решить задачу ЛП о назначениях, используя Венгерский алгоритм.
3
8
2
10
3
8
7
2
9
7
6
4
2
7
5
8
4
2
3
5
9
10
6
9
10
40