Преобразование графиков тригонометрических функций

1. Преобразование графиков тригонометрических функций

План урока
1.
2.
3.
4.
Организационный момент;
Фронтальный опрос;
Выполнение упражнений : построение графиков функций;
Подведение итогов.

2.

Цель урока:
1. Отработать и и закрепить навыки
построения графиков функций у=-f(x), у=f(x + a),
у=f(x) + b, у= mf(x), у=f(kx), у=f(kx + a) зная график
функции у=f(x).
2. Совершенствовать навыки решения упражнений
и построения графиков тригонометрических
функций.

3.

1. Графики функций у=f(x +a ), у=f(x )+b, у=f(x +а)+b
получаются из графика функции у=f(x ) путём параллельного переноса
на lаІ единиц масштаба вправо или влево вдоль оси х
и на lвІ единиц масштаба вверх или вниз вдоль оси у.
2. График функции у=mf(x )
получается из графика функции у=f(x ) путём растяжения от оси х
с коэффициентом m. (если m< 1, то говорят о сжатии к оси х
с коэффициентом 1\m).
3. График функции у= -f(x )
получается из графика функции у=f(x ) путём преобразования
симметрии относительно оси х.
4. График функции у= f(kx )
получается из графика функции у=f(x ) с помощью сжатия к оси у
с коэффициентом k, если 0<k<1, то говорят о растяжении от оси у
с коэффициентом 1/k.

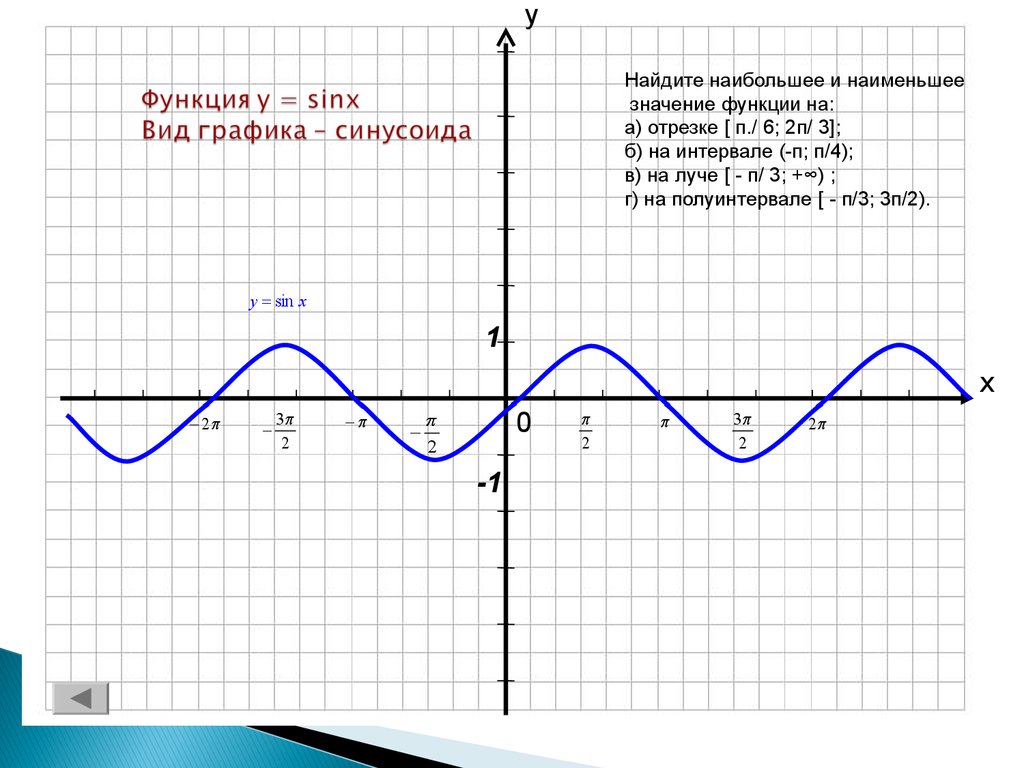
4. Функция y = sinx Вид графика – синусоида

у
Найдите наибольшее и наименьшее
значение функции на:
а) отрезке [ п./ 6; 2п/ 3];
б) на интервале (-п; п/4);
в) на луче [ - п/ 3; +∞) ;
г) на полуинтервале [ - п/3; 3п/2).
у sin x
1
х
2
3
2
0
2
-1
2
3
2
2

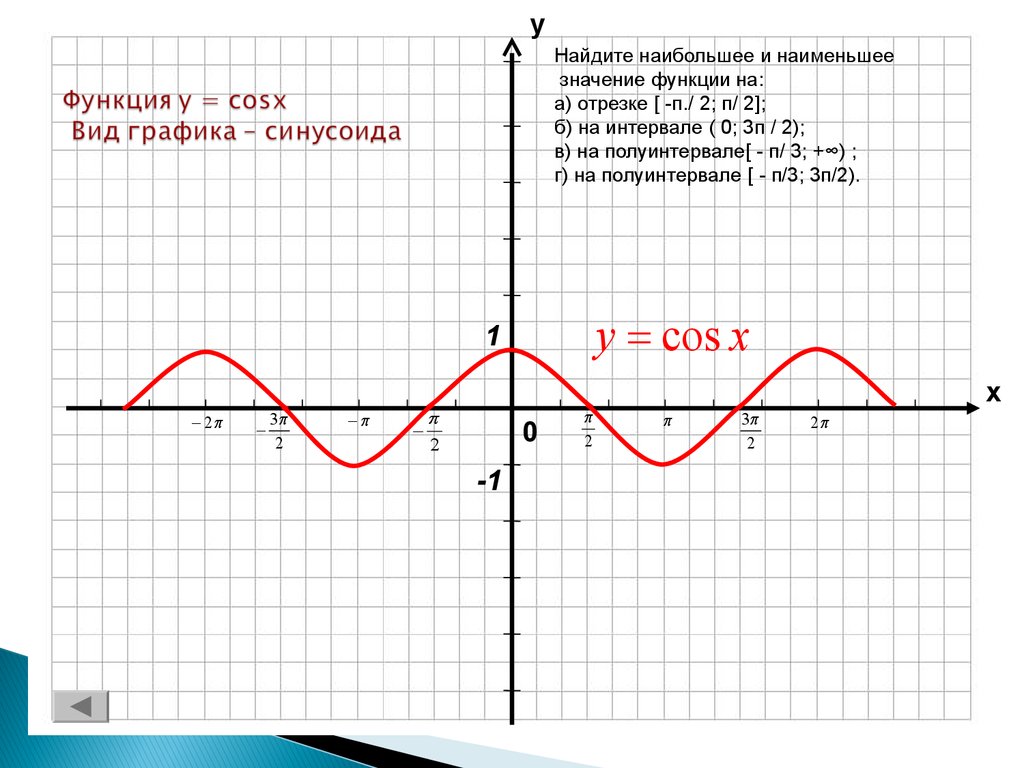
5. Функция y = cosx Вид графика – синусоида

у
Найдите наибольшее и наименьшее
значение функции на:
а) отрезке [ -п./ 2; п/ 2];
б) на интервале ( 0; 3п / 2);
в) на полуинтервале[ - п/ 3; +∞) ;
г) на полуинтервале [ - п/3; 3п/2).
у cos x
1
2
3
2
2 3 3 2
2 2 2 2
2
0
-1
2
3
2
х
2

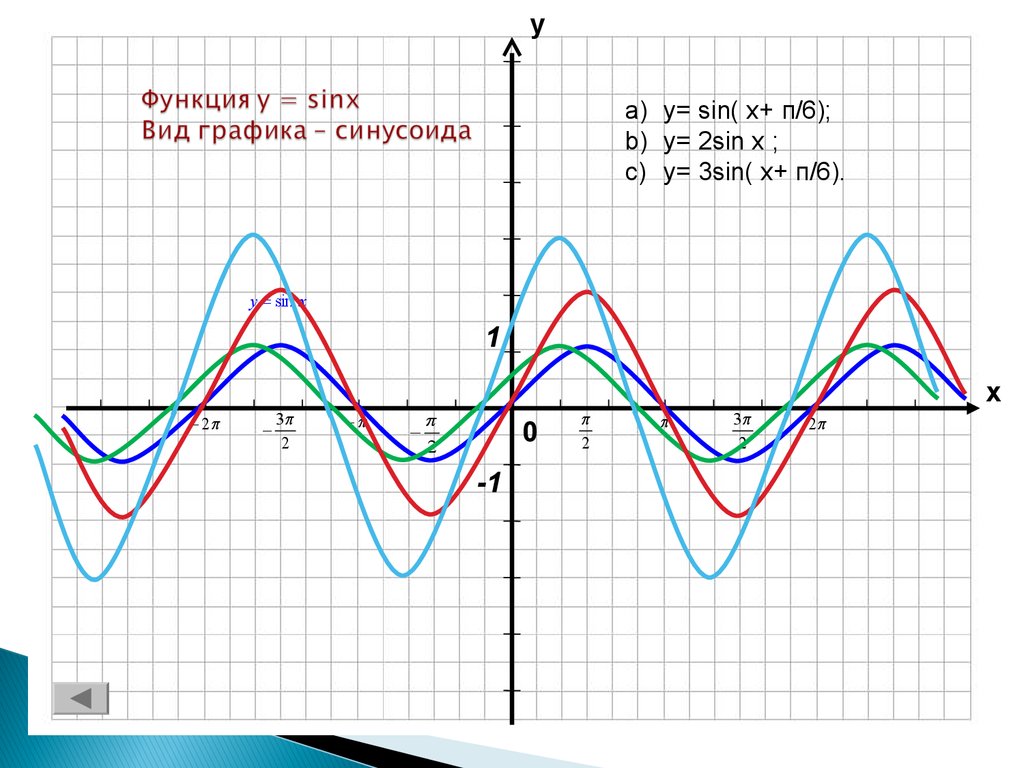
6. Функция y = sinx Вид графика – синусоида

у
a) y= sin( x+ п/6);
b) y= 2sin x ;
c) y= 3sin( x+ п/6).
у sin x
1
2
3
2
2
0
-1
2
3
2
х
2

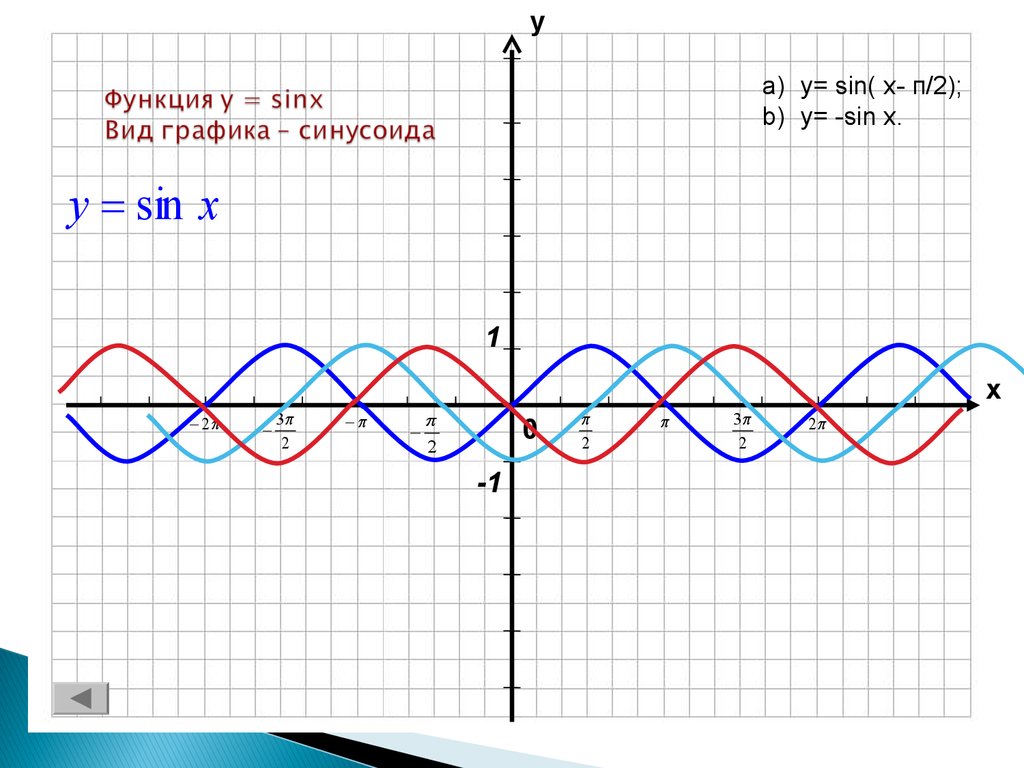
7. Функция y = sinx Вид графика – синусоида

у
a) y= sin( x- п/2);
b) y= -sin x.
у sin x
1
х
2
3
2
2
0
-1
2
3
2
2

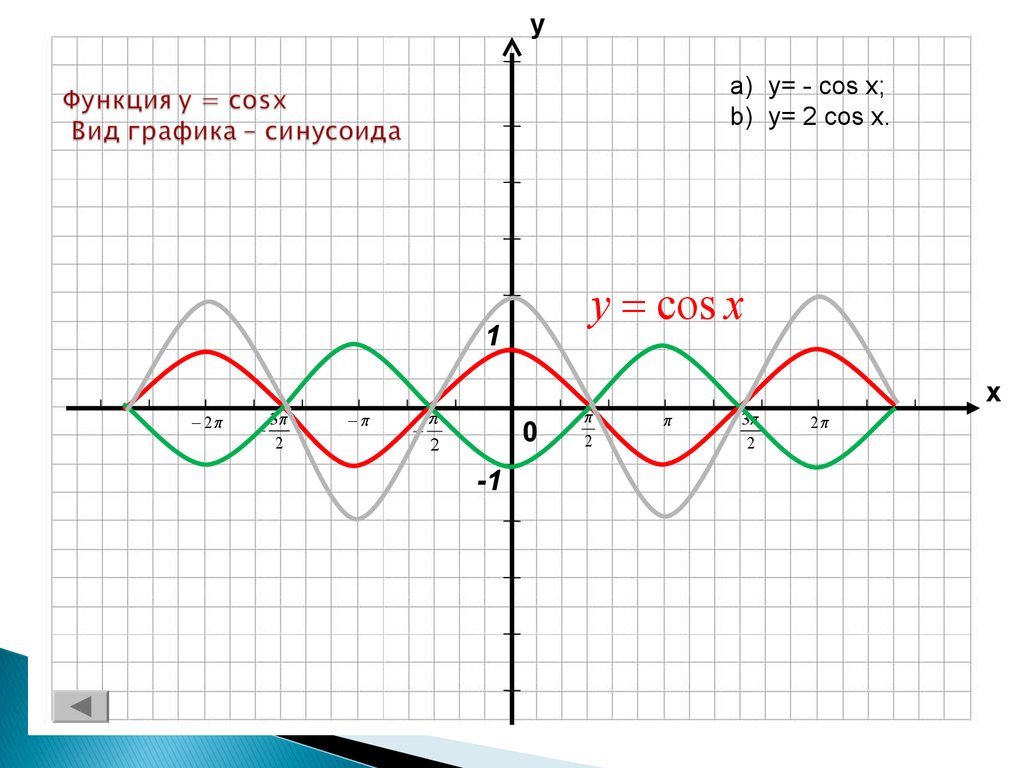
8. Функция y = cosx Вид графика – синусоида

у
a) y= - cos x;
b) y= 2 cos x.
у cos x
1
2
3
2
2 3 3 2
2 2 2 2
2
0
-1
2
3
2
х
2

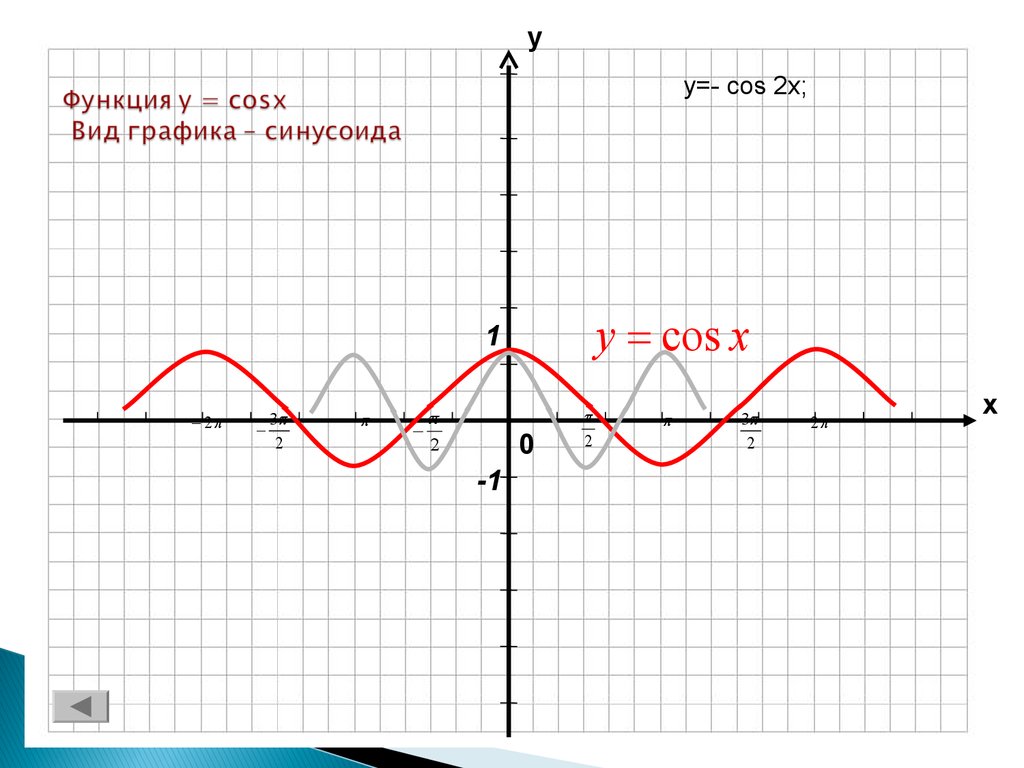
9. Функция y = cosx Вид графика – синусоида

у
y=- cos 2x;
у cos x
1
2
3
2
2 3 3 2
2 2 2 2
2
0
-1
2
3
2
2
х

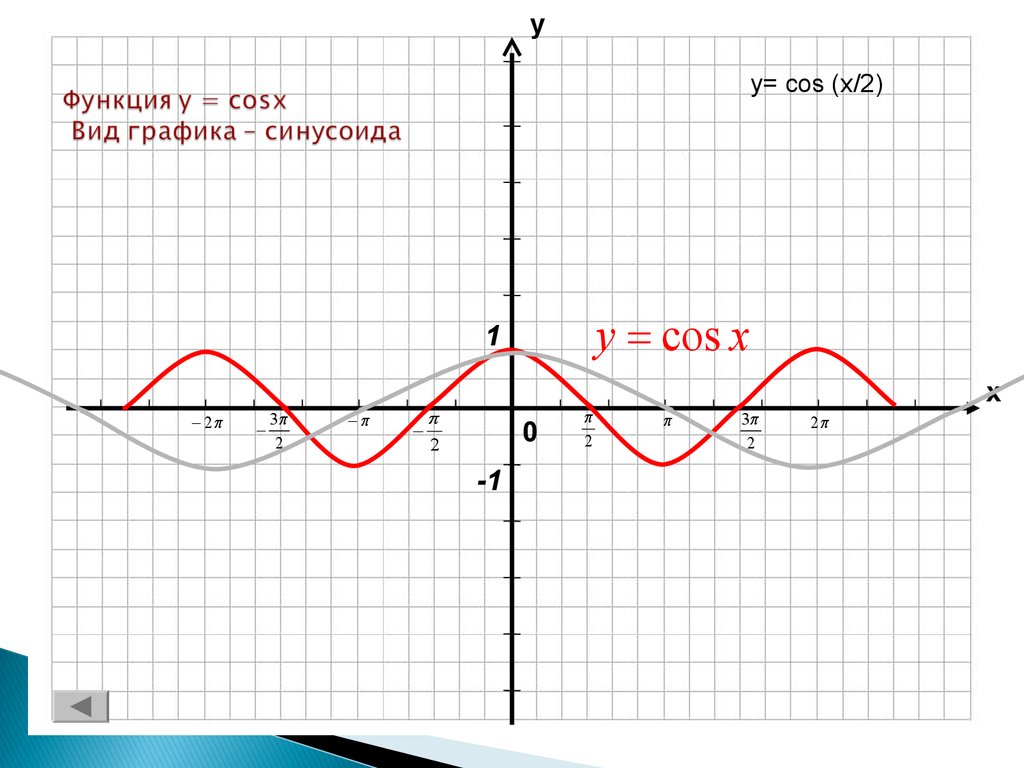
10. Функция y = cosx Вид графика – синусоида

у
y= cos (x/2)
у cos x
1
2
3
2
2 3 3 2
2 2 2 2
2
0
-1
2
3
2
х
2

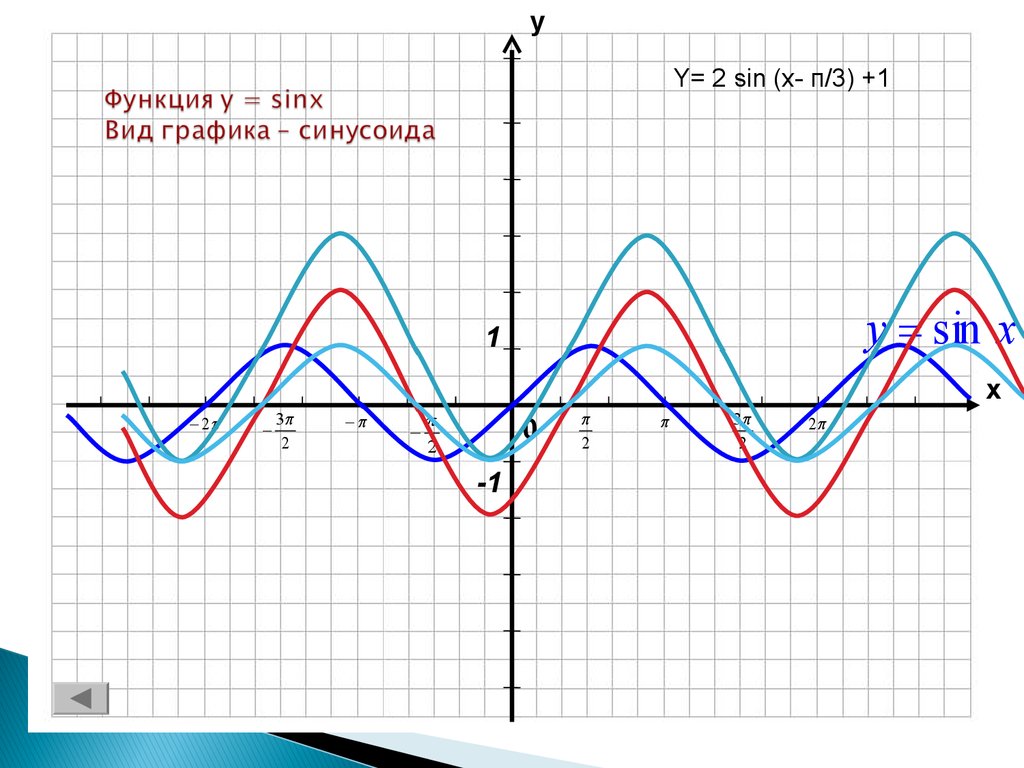
11. Функция y = sinx Вид графика – синусоида

у
Y= 2 sin (x- п/3) +1
у sin x
1
х
2
3
2
2
0
-1
2
3
2
2

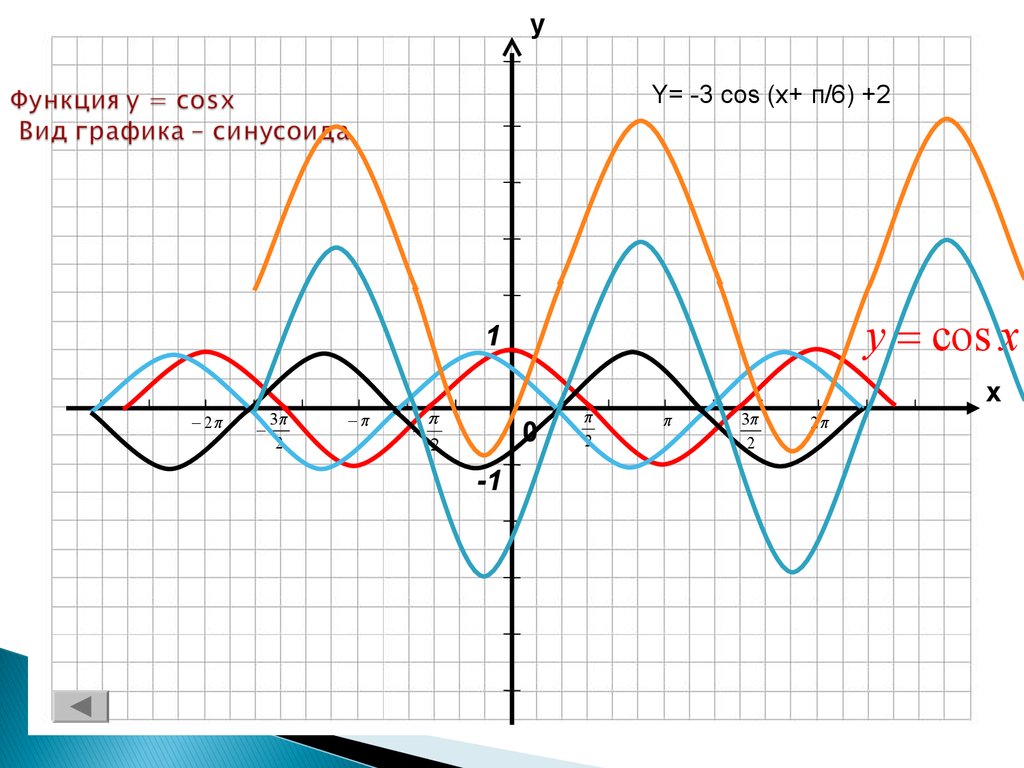
12. Функция y = cosx Вид графика – синусоида

у
Y= -3 cos (x+ п/6) +2
у cos x
1
2
3
2
2 3 3 2
2 2 2 2
2
0
-1
2
3
2
х
2

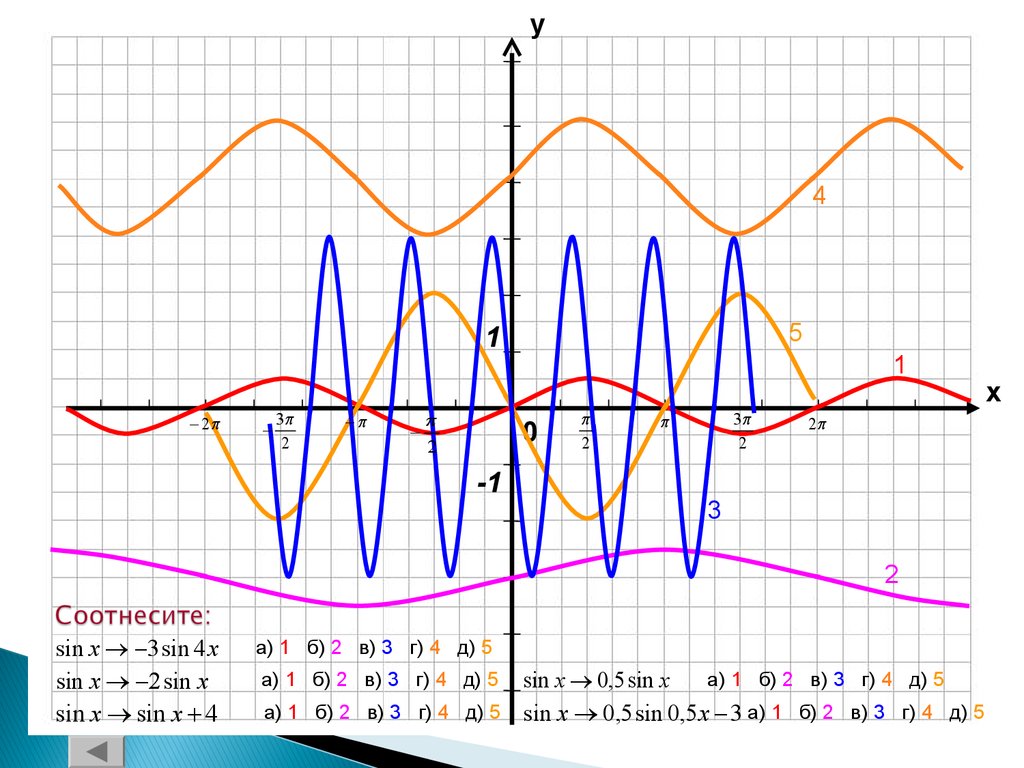
13. Соотнесите:

у
4
5
1
2
3
2
2
1
0
2
3
2
-1
2
3
2
sin x 3 sin 4 x
sin x 2 sin x
sin x sin x 4
а) 1 б) 2 в) 3 г) 4 д) 5
a) 1 б) 2 в) 3 г) 4 д) 5
sin x 0,5 sin x
а) 1 б) 2 в) 3 г) 4 д) 5
sin x 0,5 sin 0,5 x 3 а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
х

14. Соотнесите:

у
3
1
1
2
3
2
2
0
-1
cos x cos( x ) а)а 1 б) 2 в) 3
3
cos x 2 cos( x ) а) 1 б) 2 в) 3
6
cos x cos( x ) а) 1 б) 2 в) 3
6
2
3
2
2
х
2