дискретная структура 1

1.

1-тема. Введение. Математическая речь
(Speaking Mathematically).
План:
1.Математическая логика. Понятие высказывания.
2. Простые и сложные высказывания: истинность и ложность,
обозначение.
3. Теория множеств. Множество.Способы задания
множеств.Элементы и типы множеств.Универсальное
множество . Декартово произведение. Упорядоченные
пары.Отношения в ограниченных множествах и понятие
функции.
.

2.

3.

4.

*Логика – наука, изучающая законы и формы мышления;
учение о способах рассуждений и доказательстве.
*Математическая логика составляет значительную
часть дискретной математики. Алгебра высказываний
является начальным разделом математической логики.
Математическая логика вместе с теорией множеств
является фундаментом, на котором построена вся
современная математика.

5.

С прикладной точки зрения математическая логика
составляет основу для построения языков
программирования, играет большую роль при
построении банков данных, банков знаний и вообще во
всех вопросах, связанных с искусственным интеллектом.
С общеобразовательной точки зрения математическая
логика представляет интерес тем, что она позволяет
изучать общие логические законы, которые мы постоянно
применяем при рассуждениях и дискуссиях (закон
двойного отрицания, закон противоречия, закон
исключенного третьего и т. п.).
Таким образом, математическая логика может служить
хорошим инструментом для тех, кто желает научиться
точному аналитическому мышлению .

6.

*Под высказыванием мы понимаем утверждение или
повествовательное предложение какого-либо языка, о
содержание которого можно сказать, истинно оно или
ложно(т.е.говорят,что оно имеет значение истинности:
может быть истинным, то обозначается буквой И или
ложным ,то - Л )( в дальнейшем мы дадим более строгое
определение!)
Повелительные («Войдите, пожалуйста»), вопросительные
(«Который час?») и бессмысленные предложения («Сумма пяти и
восемнадцати»), в которых ничего не утверждается, не являются
высказываниями! Не будет высказыванием утверждение,
истинность или ложность которого нельзя определить однозначно.
Например: «Музыка Вагнера очень мелодична», «Картины Пикассо
слишком абстрактны».

7.

Высказывание называется простым,
если никакая его часть сама не
является высказыванием.
Высказывание, состоящие из
простых высказываний, называется
сложным или составным.
*Высказывания мы будем обозначать
заглавными буквами латинского
алфавита, возможно с индексами: A ,B
,X ,Y, C1 ,A1 ….

8.

Основные логические связки это связки: и, или, не, если … то…,
которые в логике высказываний имеют специальные названия и
обозначения. Иногда к ним добавляют еще две связки либо …, либо
…(или …, или …); если, и только если (тогда и только тогда).
* Используя их, можно построить новые высказывания, называемые
«сложные или составные высказывания».
Если мы рассматриваем высказывания и операции над ними, то
можно говорит об «алгебре логики».
В формулах алгебры логики переменные – это высказывания.
Они принимают только 2 значения – ложь и истина, которые
обозначаются либо Л и И, либо false и true,
либо 0 и 1.
Каждая формула задает логическую функцию, которая сама может
принимать только два логических значения.

9.

Если высказывание А истинно, то можно писать А=1;
если высказывание А ложно, то А=0.

10.

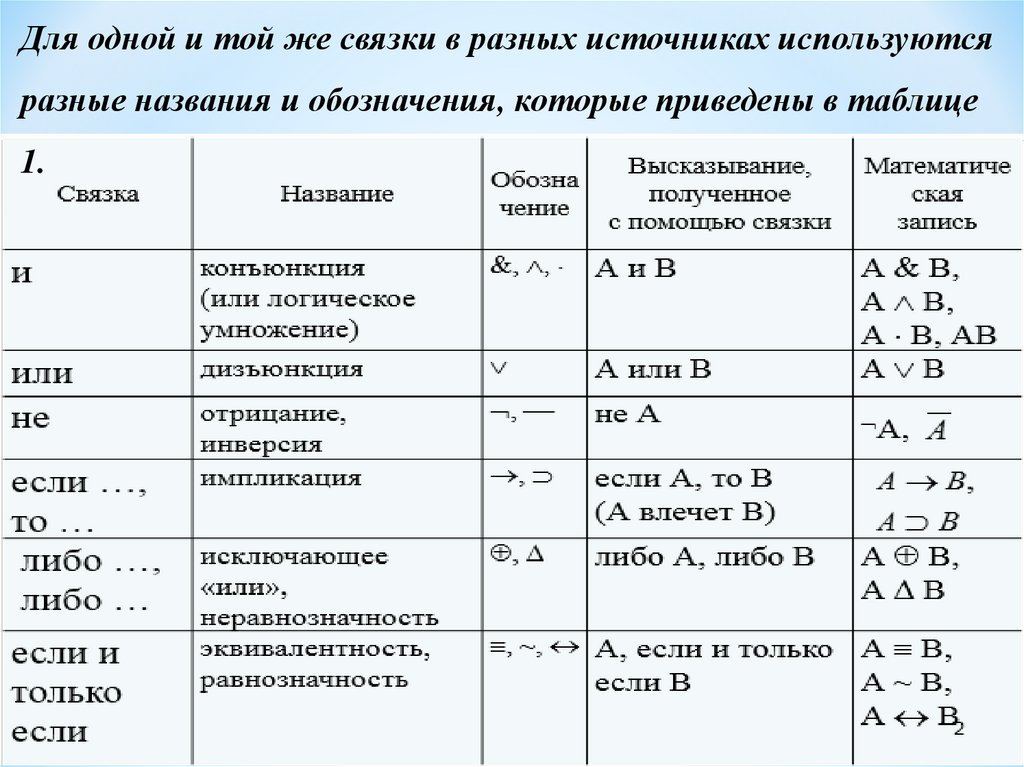
Для одной и той же связки в разных источниках используются
разные названия и обозначения, которые приведены в таблице
1.

11.

* Схожесть названий и форм законов алгебры логики, булевой
алгебры и соответствующих законов алгебры множеств, не
случайна.
* В таблице, приведенной ниже, устанавливается соответствие
между булевыми операциями, логическими операторами логики
высказываний и операциями над множествами:
* Таким образом, можно комбинировать булевы переменные с
булевы операциями и получать булевы выражения.

12.

ПРИМЕРЫ
1.А="два умножить на два равно семи"=0
2. В="два плюс два равно 4"=1
3. С="снег белый"=1
4. Д="если сегодня среда, то завтра будет четверг"=1
5.Х="если два плюс два равно пяти, то три плюс два равно
десяти"=?

13.

* Логические парадоксы.
Есть предложения, которые по своей структуре очень схожи с
высказываниями, но таковыми не являются. Это в дальнейшем и
приведет нас к необходимости дать строгое определение
высказывания.
* Рассмотрим следующий пример. Возьмем два листа бумаги,
пронумеруем их – номер 1 и номер 2. На первом листе напишем
высказывание "На втором листе написана ложь", на втором листе
напишем высказывание "На первом листе написана истина". На
первый взгляд обычное высказывание, ничем не отличающееся от
многих подобных, но...! Задайтесь вопросом, истинно оно или
ложно, и Вы увидите, что любое из этих предположений приводит
к противоречию, то есть о нем нельзя сказать, истинно оно или
ложно. Такие ситуации в математике и семантике называются
логическими парадоксами.
* Таким образом, существуют предложения, по форме похожее на
высказывание, но такими не являются.

14.

Из простых высказываний можно получать более сложные
(составные высказывания) с помощью так называемых
логических связок или логических операций .
Основные логические операции –сл.тема