Похожие презентации:
Симметричные составляющие
1.
Симметричные составляющиеЛектор: Каверин Н.В
СОБСТВЕННЫЕ НУЖДЫ
ПОДСТАНЦИЙ
2. Метод симметричных составляющих
Метод симметричных составляющих – это универсальныймеханизм, позволяющий анализировать повреждения в
первичной сети и создавать устройства, реагирующие на эти
повреждения
• Современные системы электроснабжения состоят из
связанных симметричных сетей трехфазного переменного
тока
• Каждый из основных элементов, входящих в эти сети
(генераторы, трансформаторы, линии и преобладающая часть
нагрузки- электродвигатели) имеют равные пофазно
сопротивления.
• Однако к линиям электропередачи, являющимися
связующими элементами сети, это положение может быть
применено только с определенным приближением.
3. Метод симметричных составляющих
• Дело в том, что расположение фазных проводов на опорах ЛЭП неявляется симметричным, и поэтому сопротивления отдельных фаз
линий оказываются не равными между собой.
• Также небольшая часть нагрузки сетей, тоже имеет неодинаковые
по фазам сопротивления (отдельные типы промышленных печей,
электротяга, освещение, некоторые виды бытовой и
производственной электроаппаратуры)
• Проблемы, связанные с несимметрией нагрузок в схемах
электроснабжения, возникли еще на ранней стадии развития
энергетики.
• Осуществление расчетов токов и напряжений при несимметричных
режимах традиционными методами оказалось очень
затрудненным.
4. Метод симметричных составляющих
Выход из сложившегося положения был предложен К.Л. Фортескью в
1918 г., создавший новый метод расчетов токов и напряжений при
несимметричных режимах в трехфазной сети переменного тока- метод
симметричных координат.
В дальнейшем метод был усовершенствован специалистами фирмы
Вестингауз К.Ф. Вагнером и Р. Д. Эвансом и опубликован в 1936 г. в
русском переводе под названием «Метод симметричных
составляющих».
Метод симметричных составляющих оказался особенно эффективным
при исследовании сложных случаев несимметрии в сетях трехфазного
тока.
Он хорошо согласуется с реальными электромагнитными процессами,
происходящими во вращающихся электрических машинах, в т.ч. в
генераторах переменного тока.
Он успешно решает задачи определения токов и напряжений при
процессах, происходящих при замыканиях на землю в элементах сети.
5. Метод симметричных составляющих
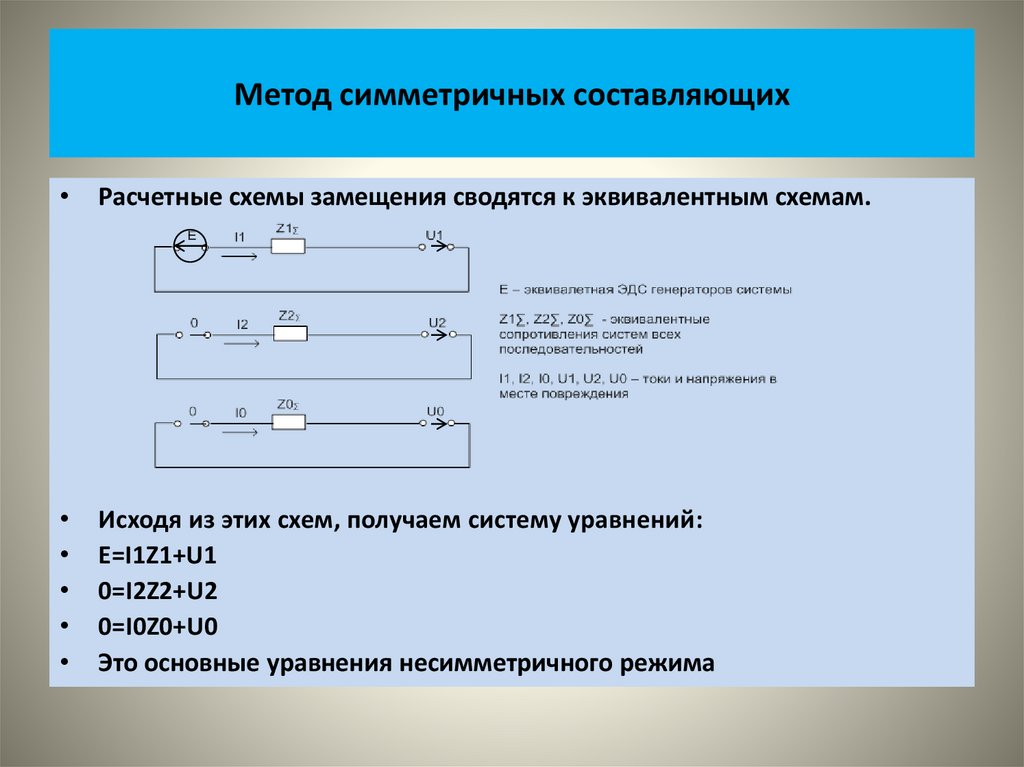
• При проведении расчетов методом симметричных составляющихшироко пользуются способом наложения.
• Основное достоинство метода- возможность исключить из расчетов
влияние взаимоиндукции между фазами элементов сети, которые
вызывают наиболее трудности.
• Это влияние учитывается путем дополнительного введения в
расчетную схему эквивалентных сопротивлений взаимоиндукции в
соответствующую фазу сети.
• В итоге решение задачи упрощается и вместо исследования явлений
в трех фазах одновременно стало возможным вести расчет для
одной, так называемой «первой» или «особой» фазы, примеряя
традиционные способы расчетов для симметричной сети.
• Метод используется при разработке устройств РЗА, в которых
применены фильтры симметричных составляющих.
6. Метод симметричных составляющих
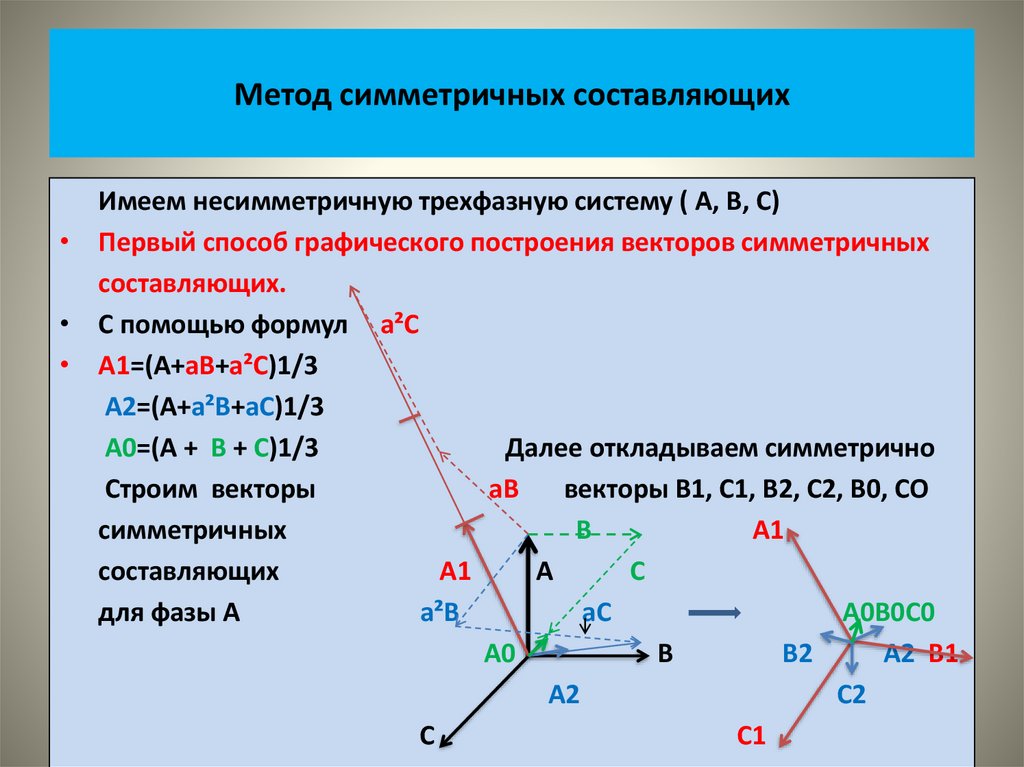
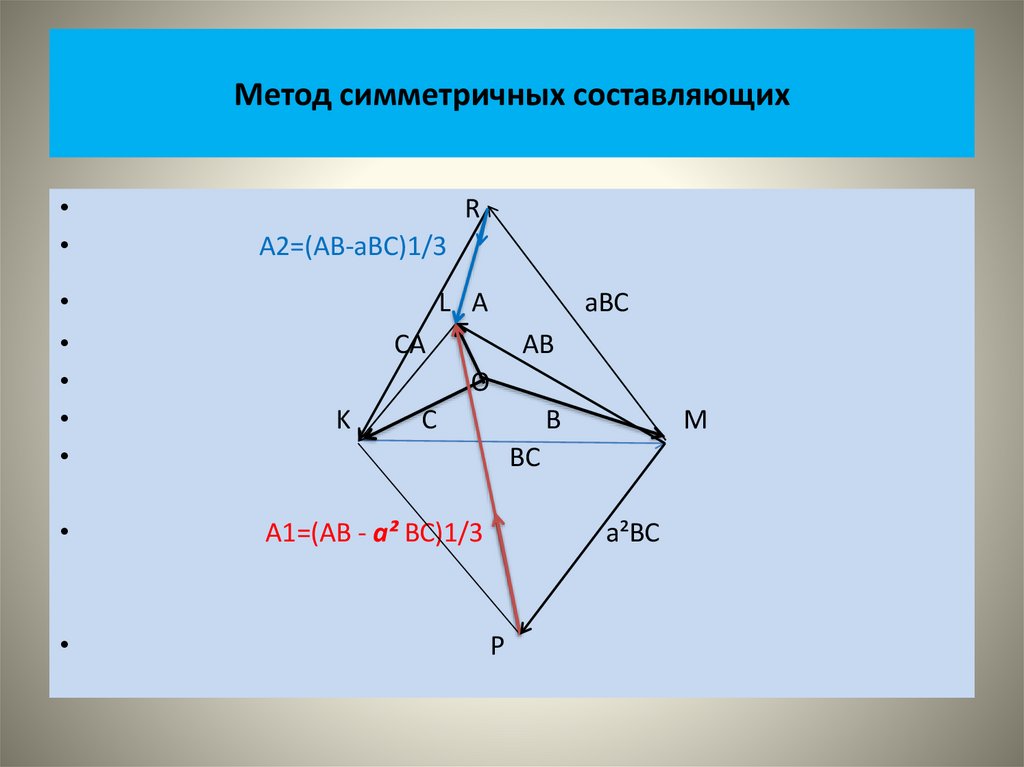
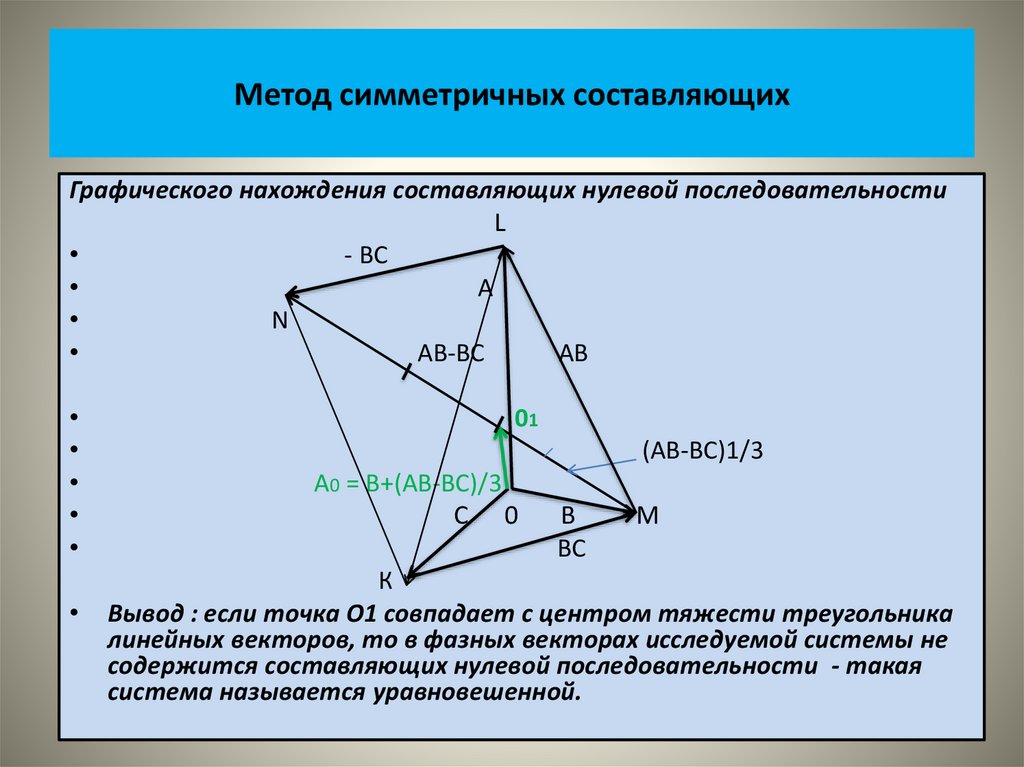
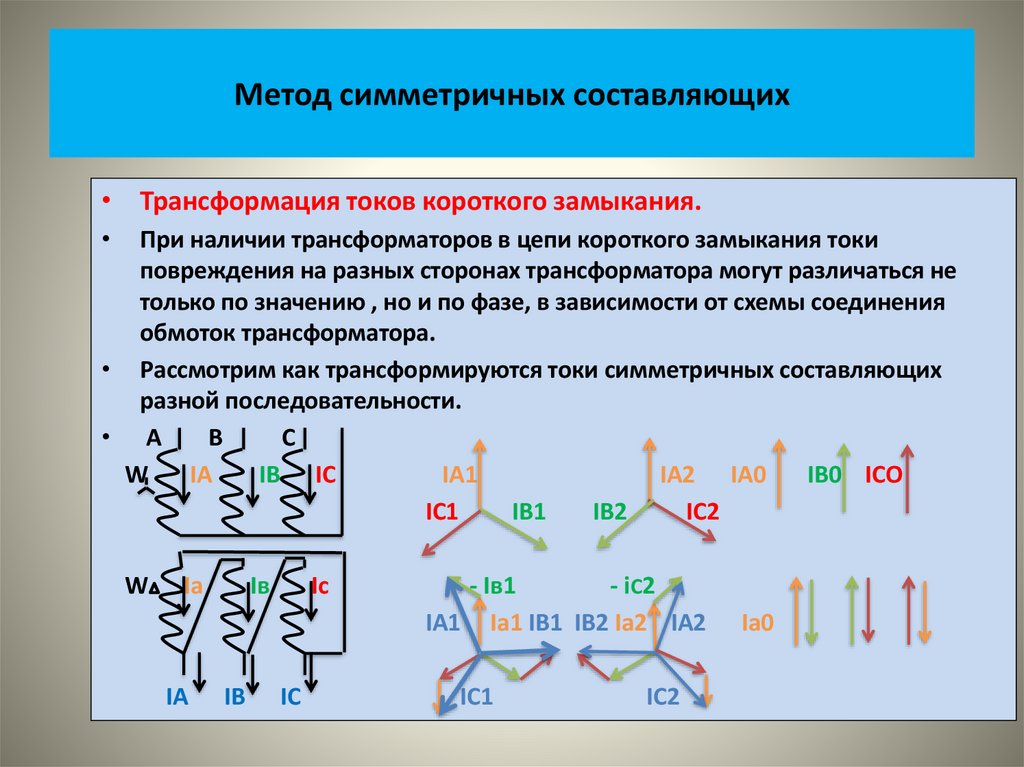
• В основе метода лежит представление о том, что любая трехфазнаянесимметричная система векторов может быть представлена в виде
отдельных трех систем векторов:
• Прямой;
• Обратной;
• Нулевой - последовательностей.
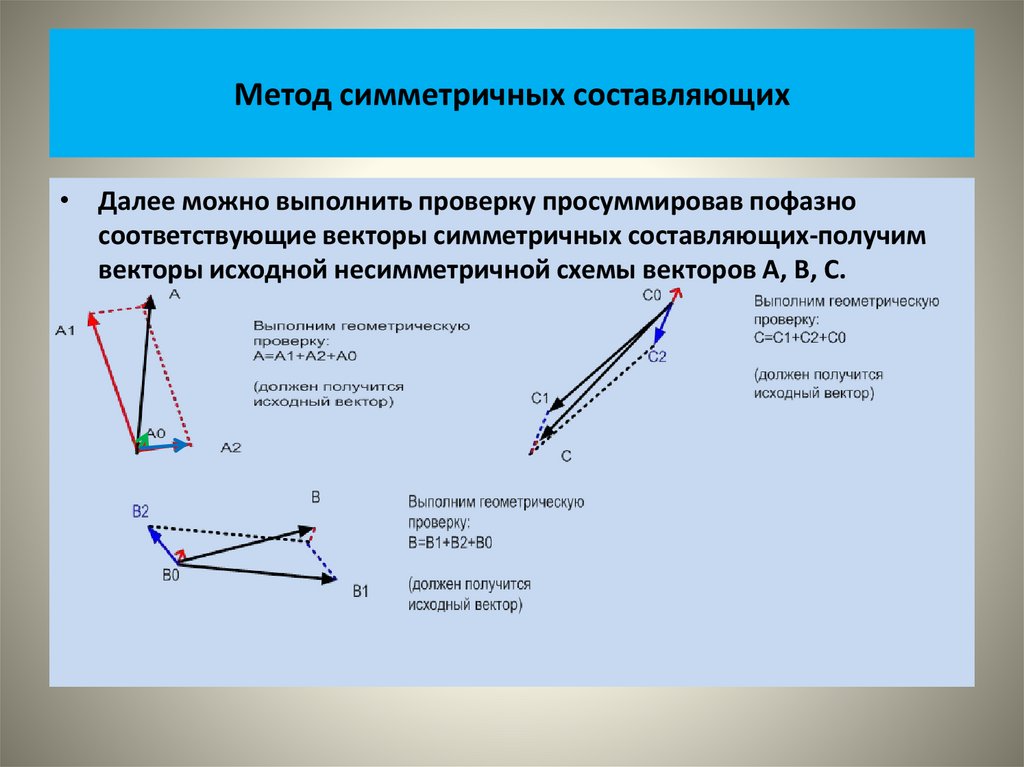
• Просуммировав пофазно соответствующие векторы симметричных
составляющих, получим векторы исходной схемы.
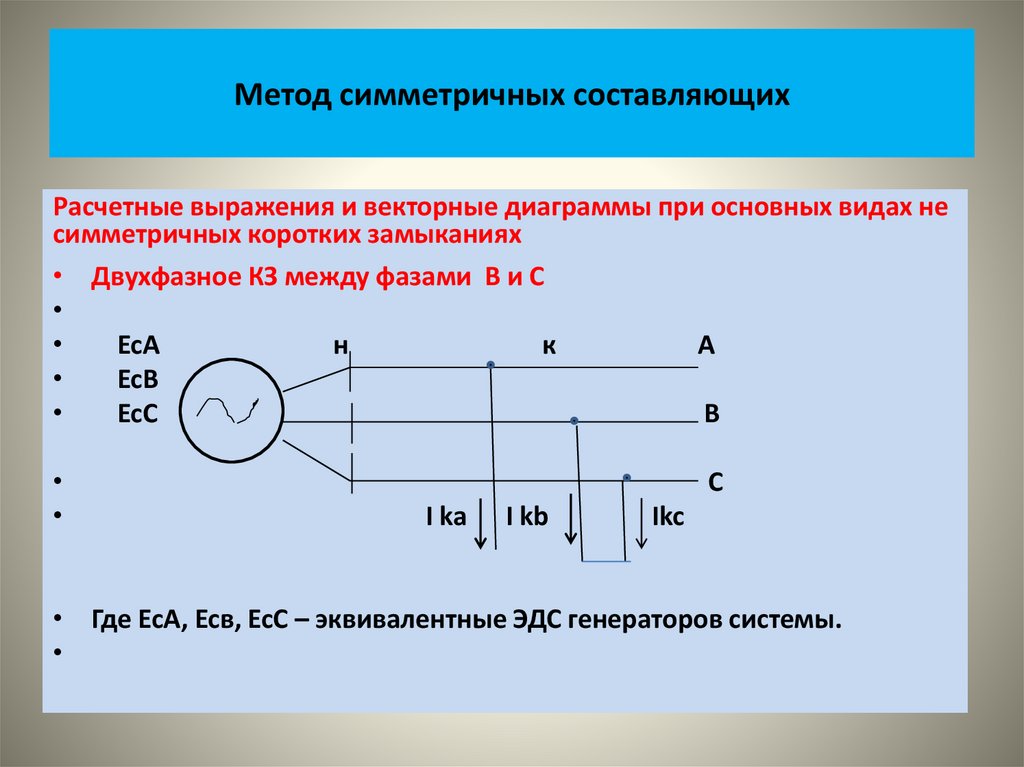
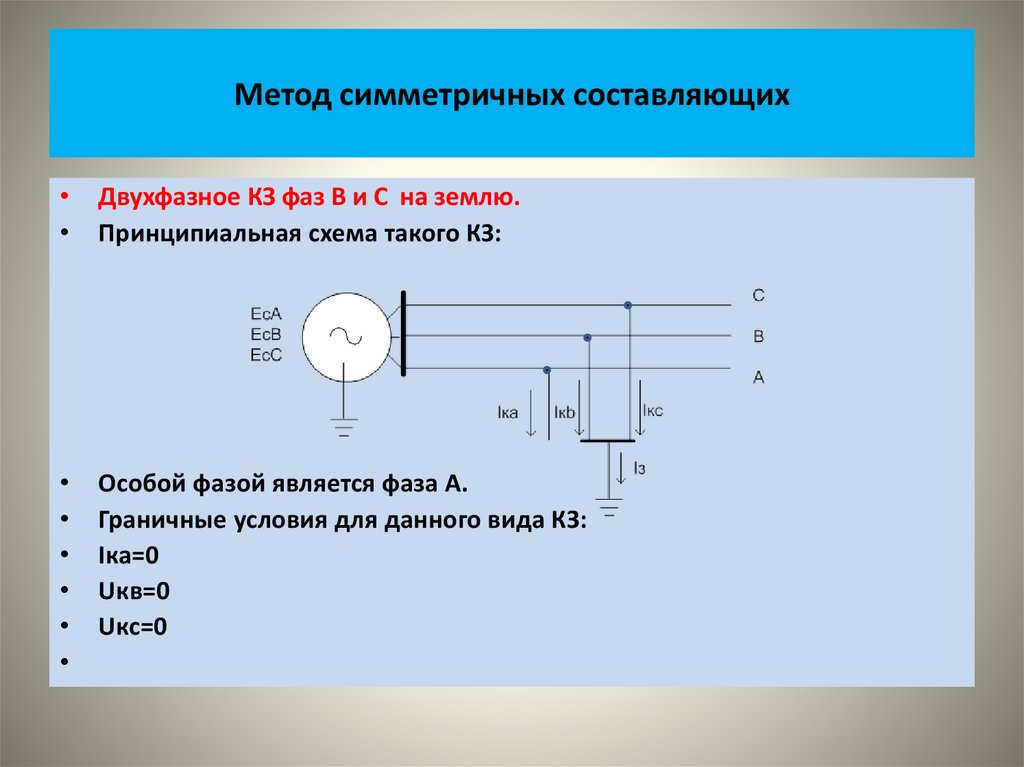
• В основе метода симметричных составляющих подразумевается, что
ЭДС источника работает в несимметричном режиме, например при
КЗ
7. Метод симметричных составляющих
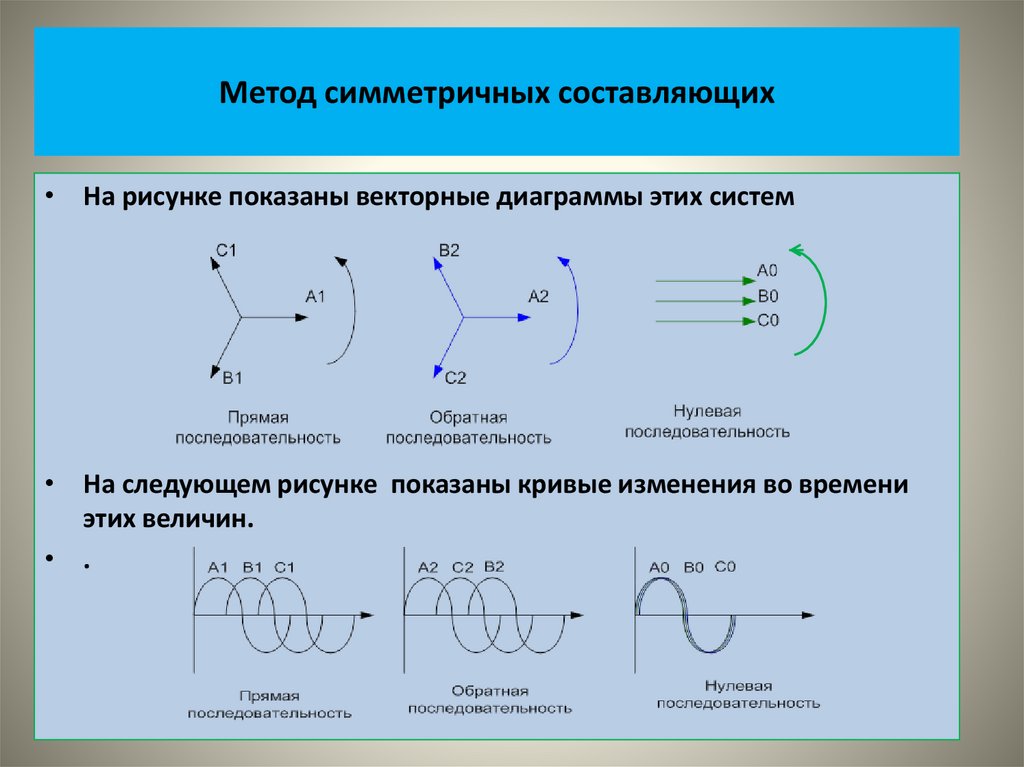
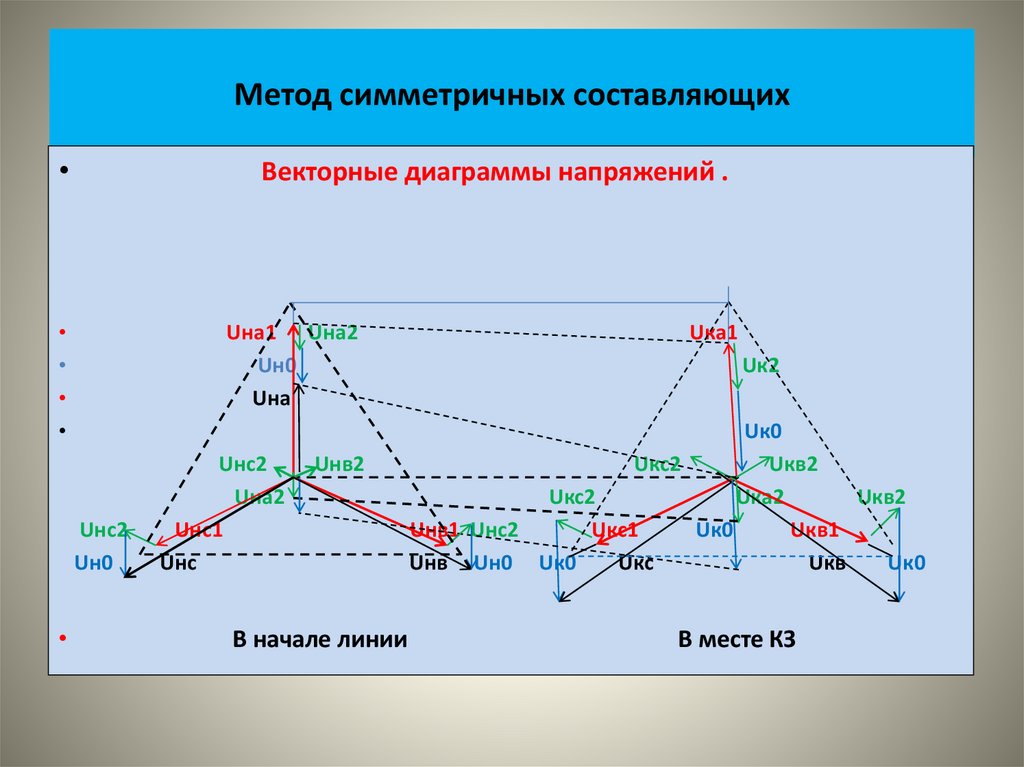
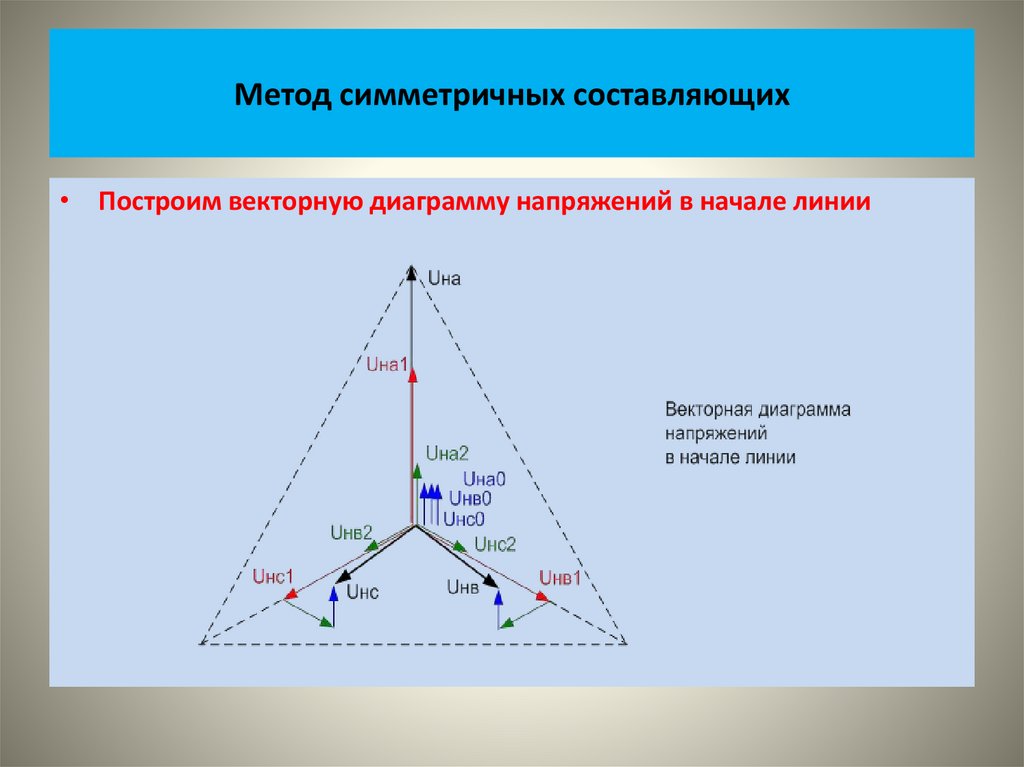
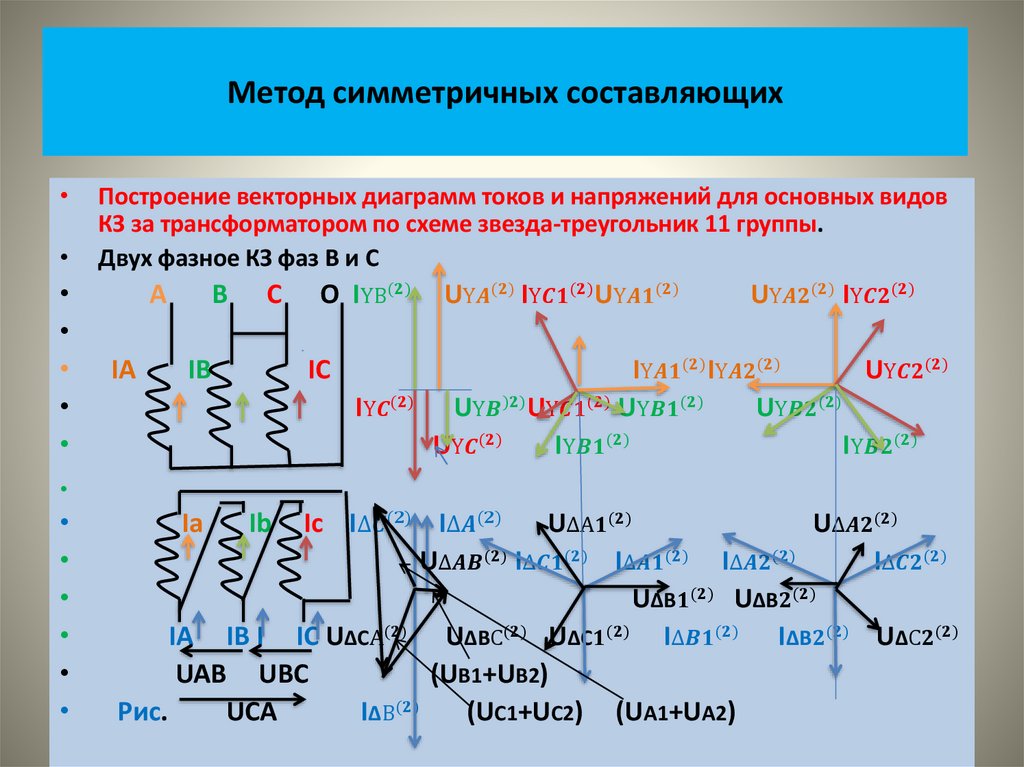
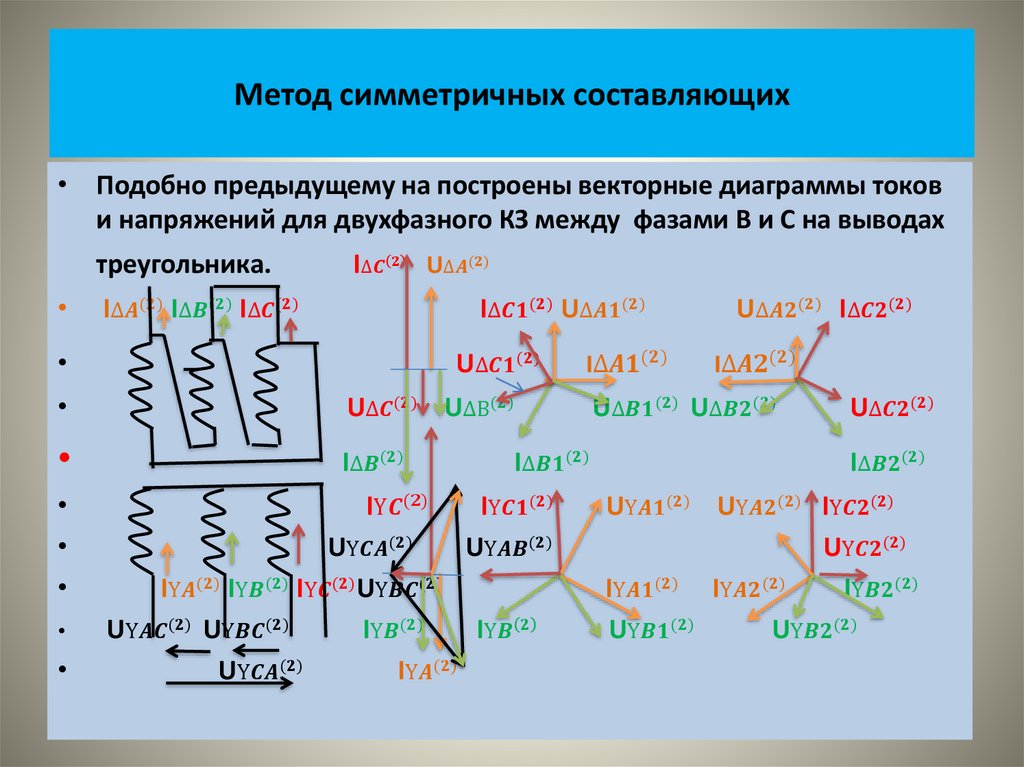
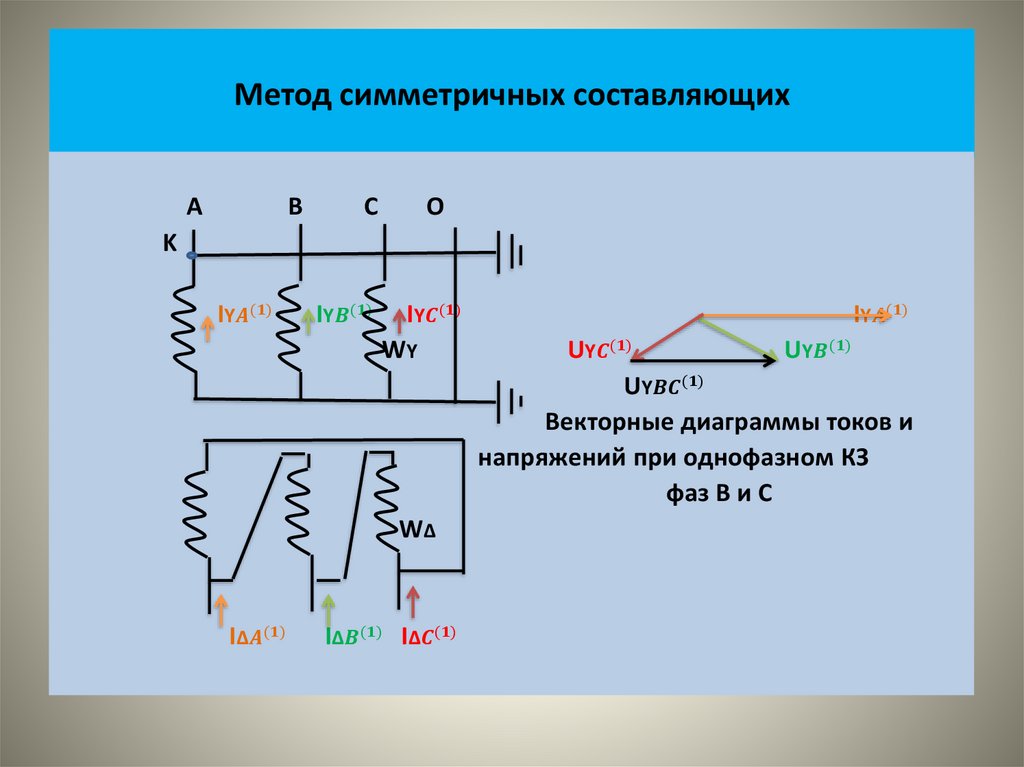
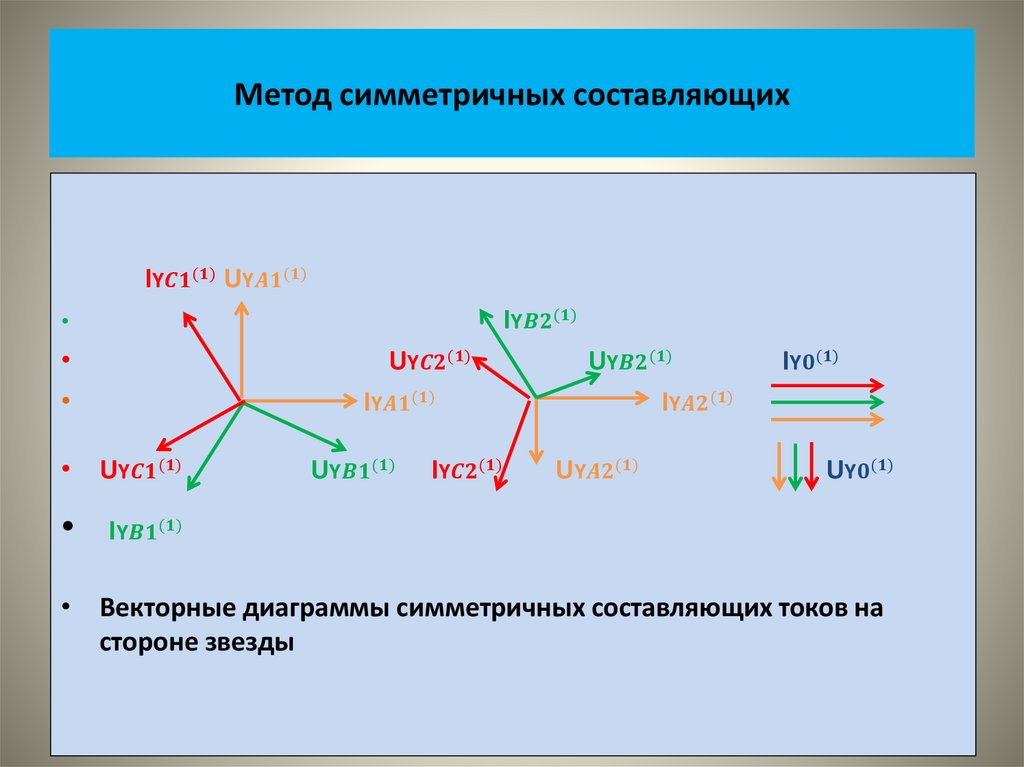
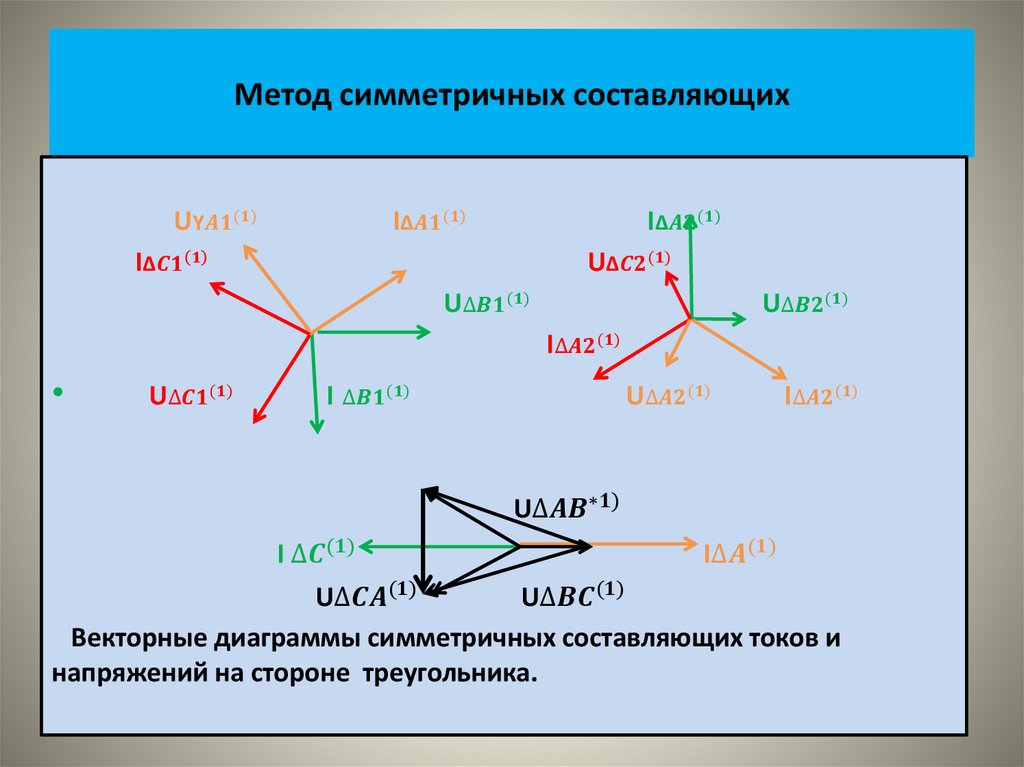
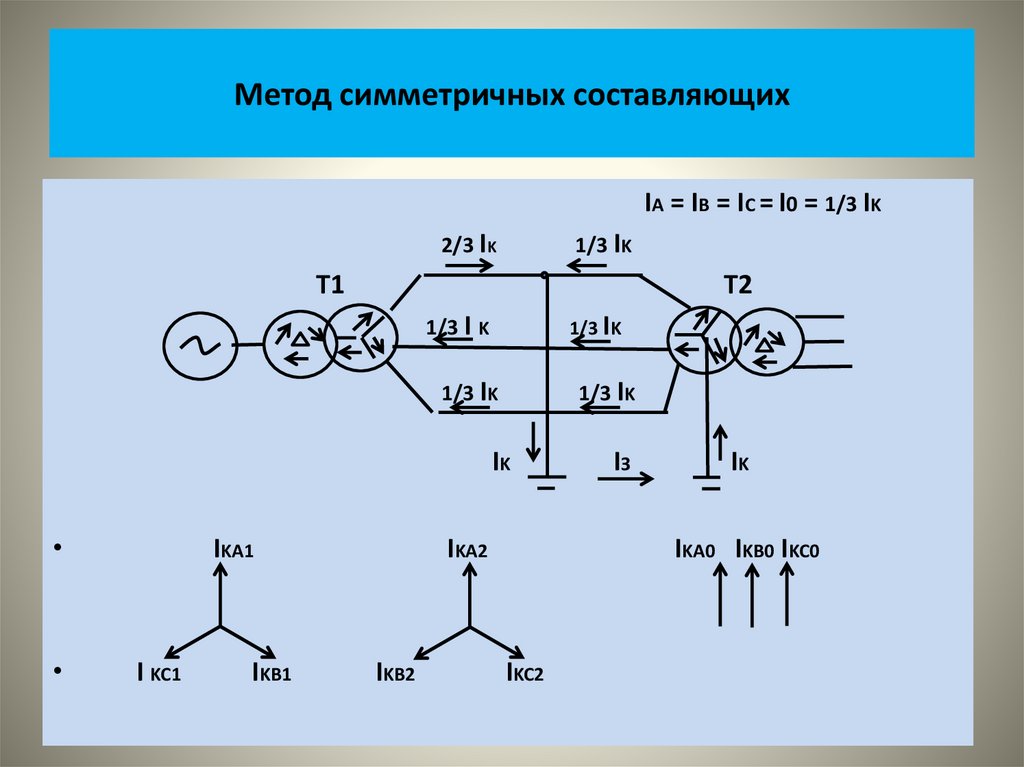
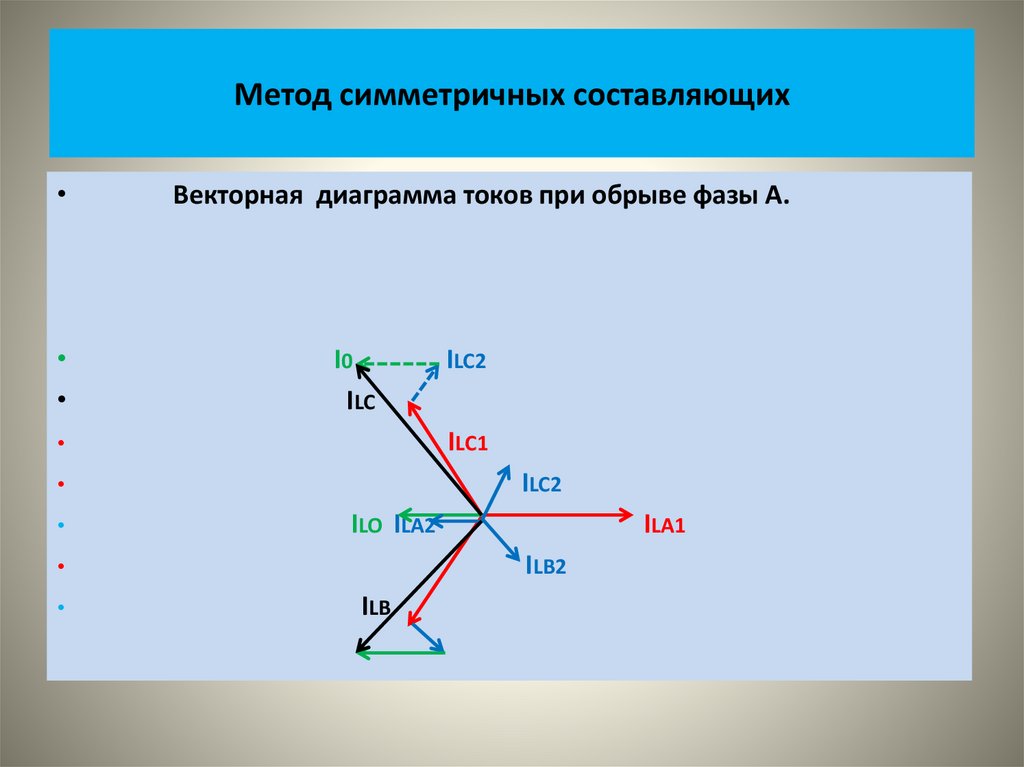
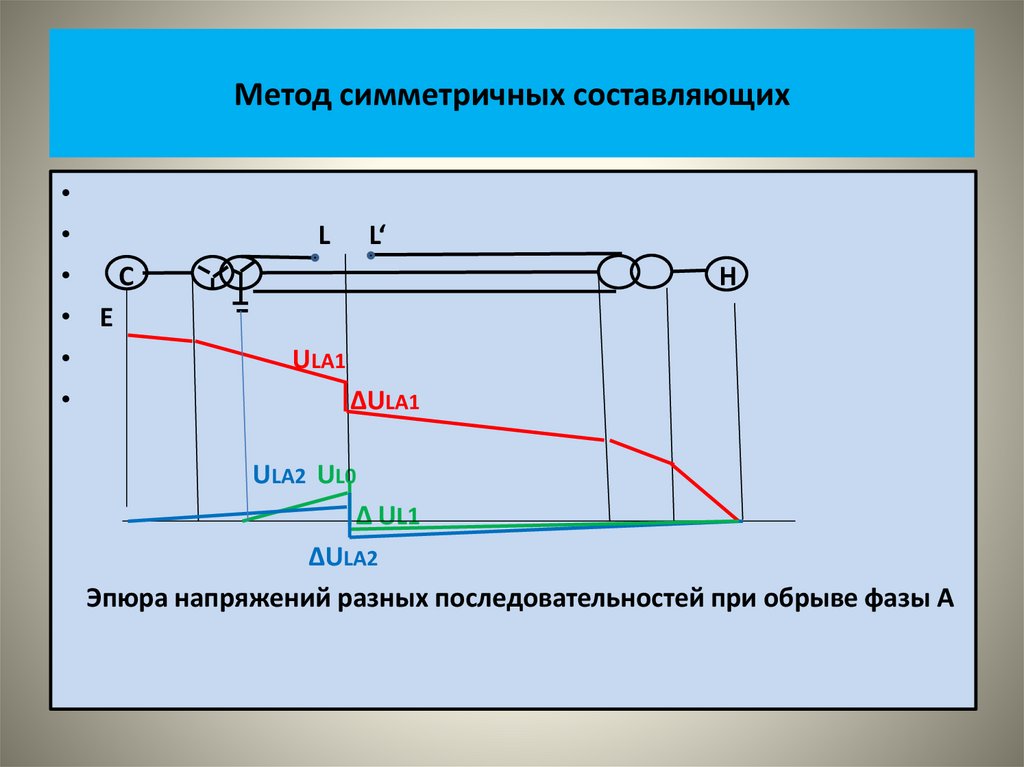
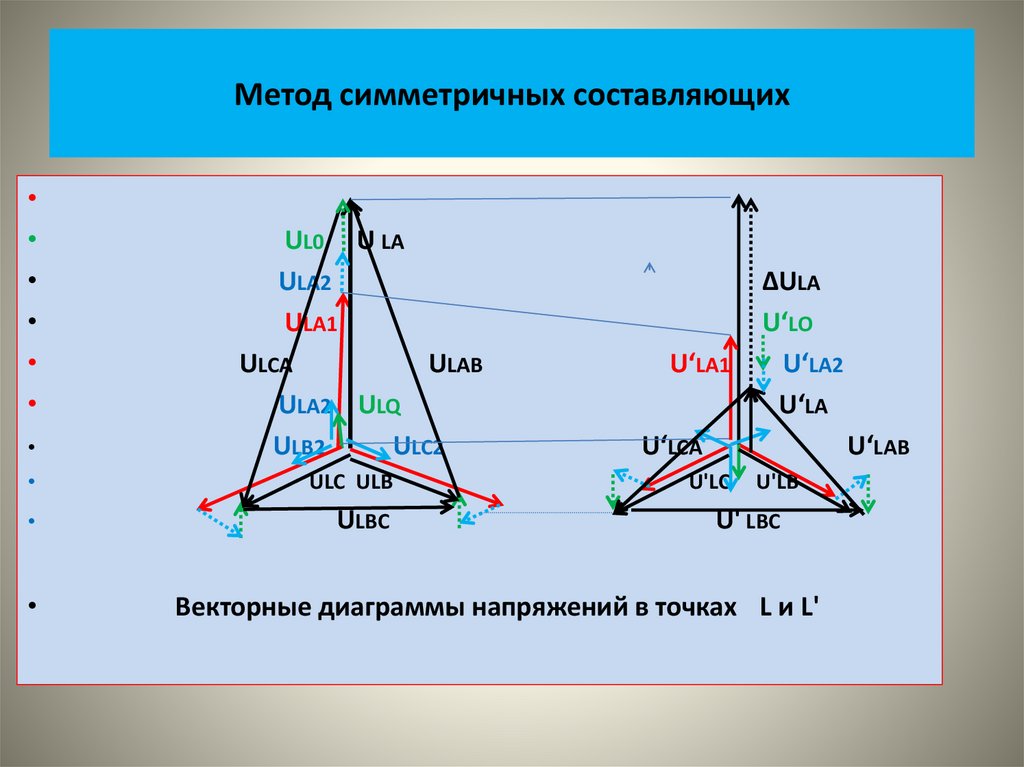
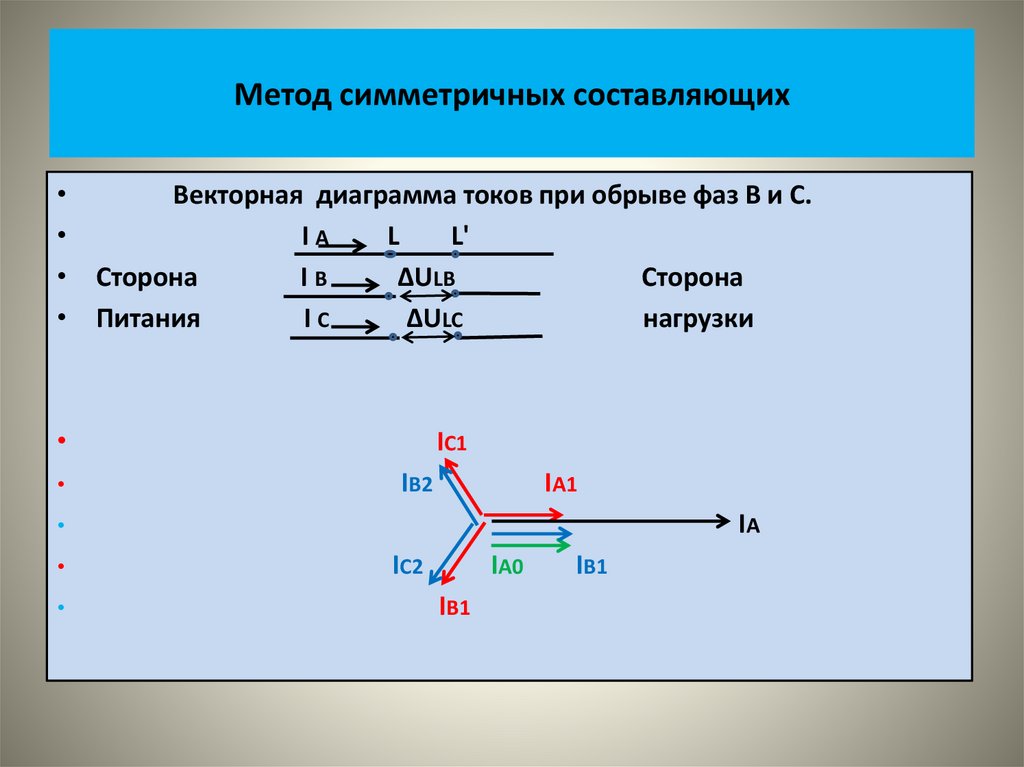
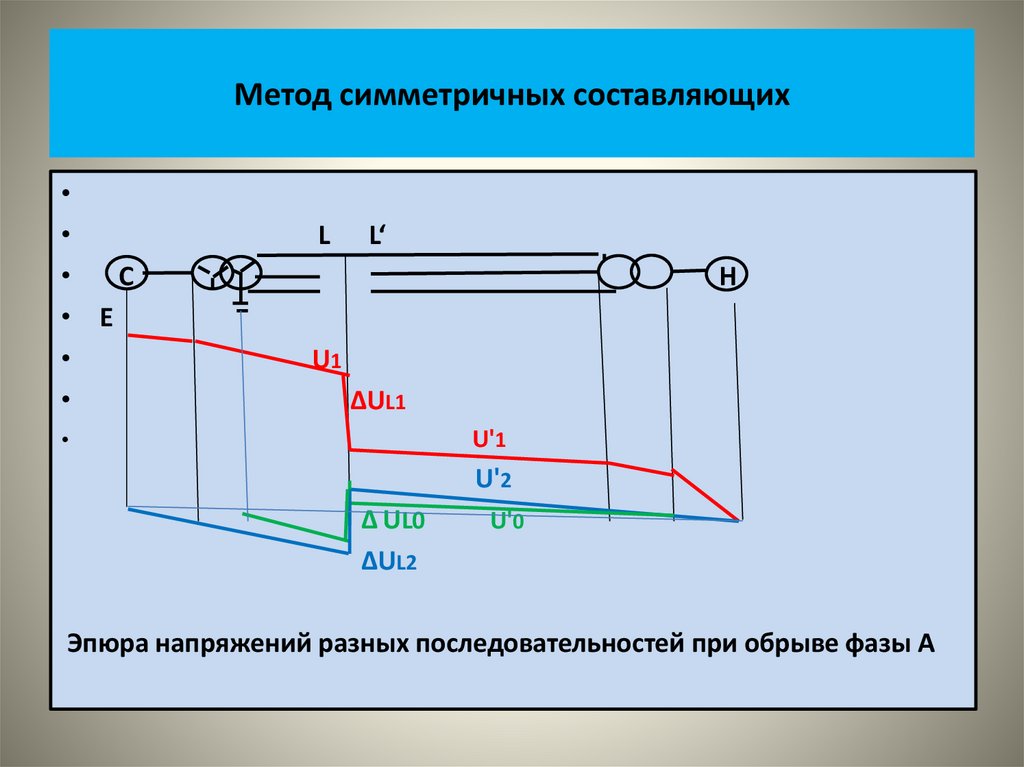
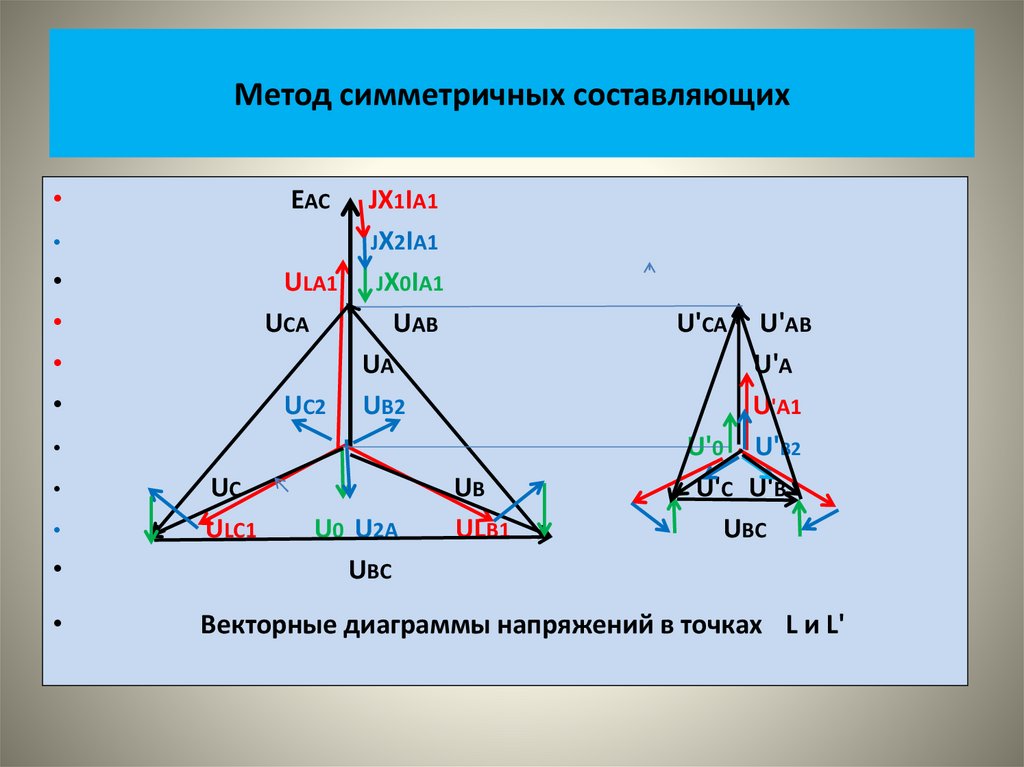
• На рисунке показаны векторные диаграммы этих систем• На следующем рисунке показаны кривые изменения во времени
этих величин.
• .
8. Метод симметричных составляющих
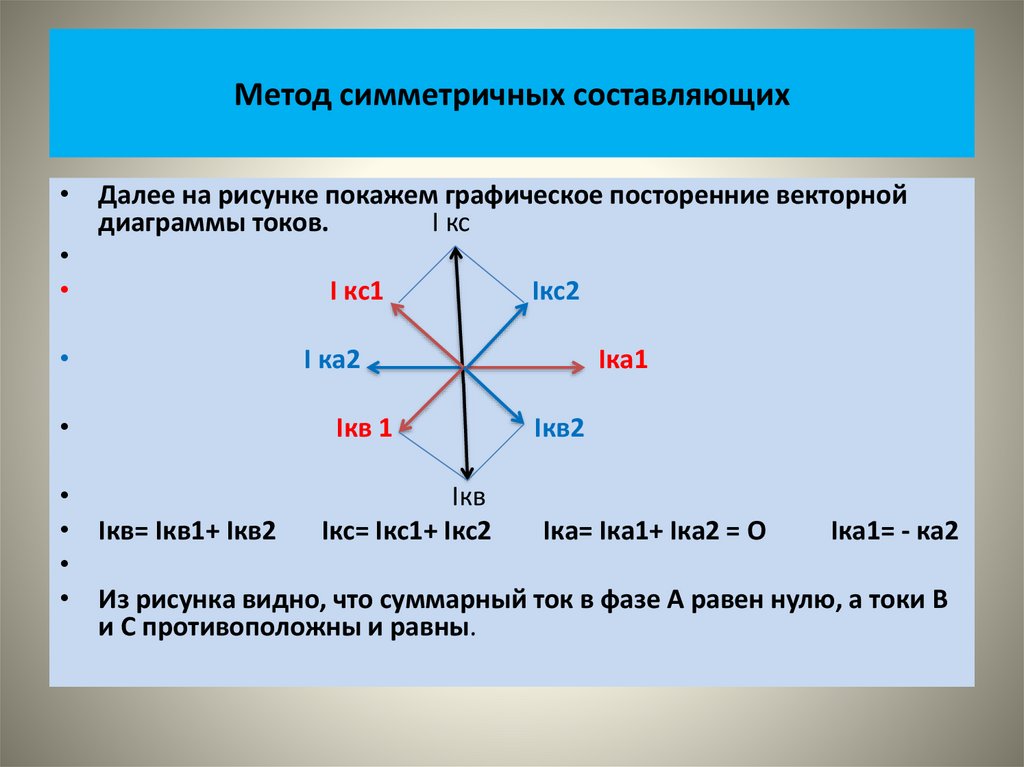
• Векторы прямой и обратной последовательностей отстоят друг отдруга на 120º.
• Векторы нулевой последовательности совпадают и по значению, и
по фазе.
Системы прямой и обратной последовательности являются
уравновешенными, то есть сумма векторов трех фаз равна нулю.
• Система нулевой последовательности – неуравновешенная, сумма
векторов равна утроенному значению одного вектора.
• Полные значения векторов несимметричной системы получаются из
геометрической суммы векторов трех симметричных систем:
• Фаза А=А1+А2+А0
• Фаза В=В1+В2+В0
• Фаза С=С1+С2+С0
9. Метод симметричных составляющих
• Оператор а и его свойства.• Для более компактной записи используют оператор фазы (или
фазный множитель)
а = е


































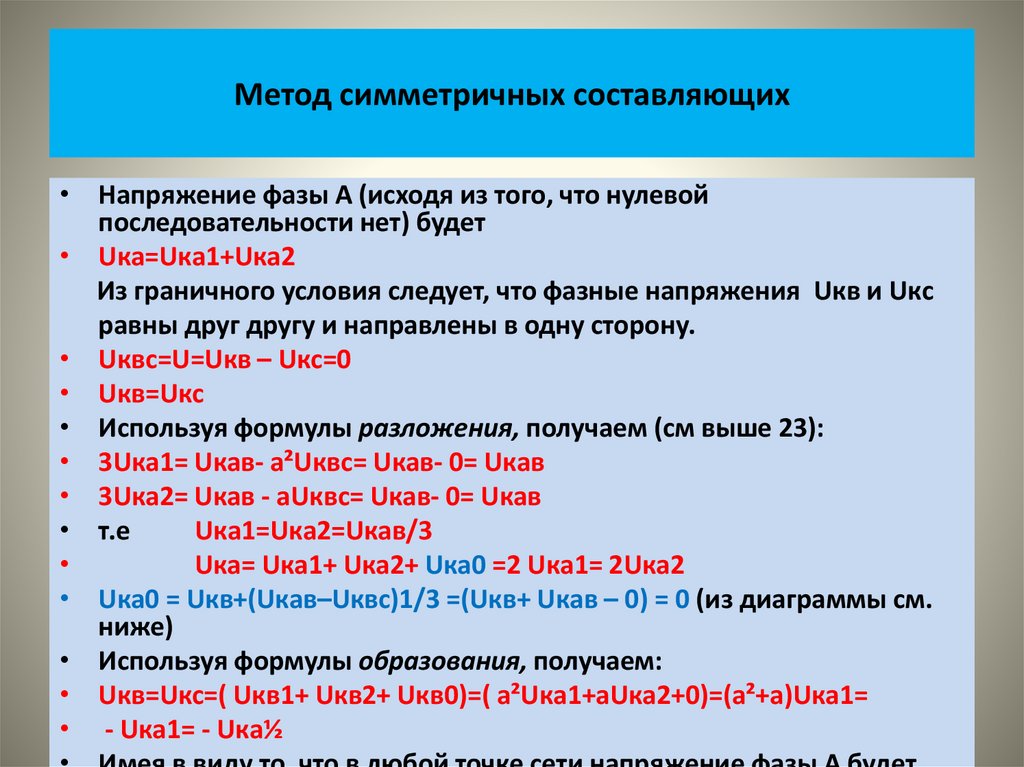


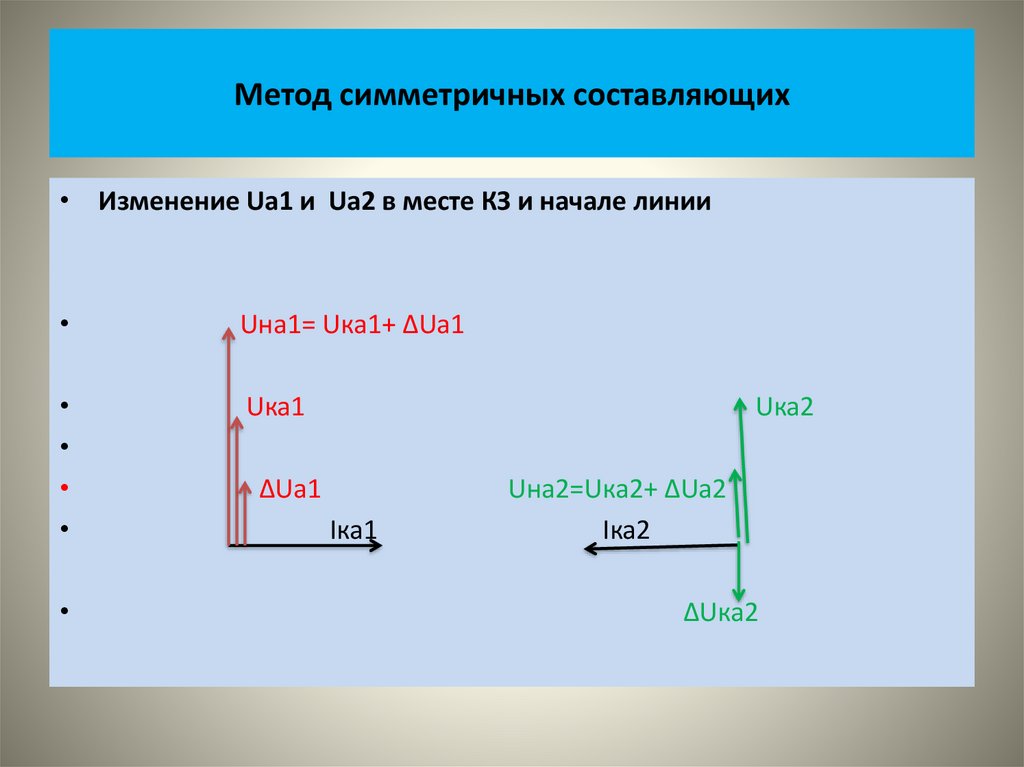
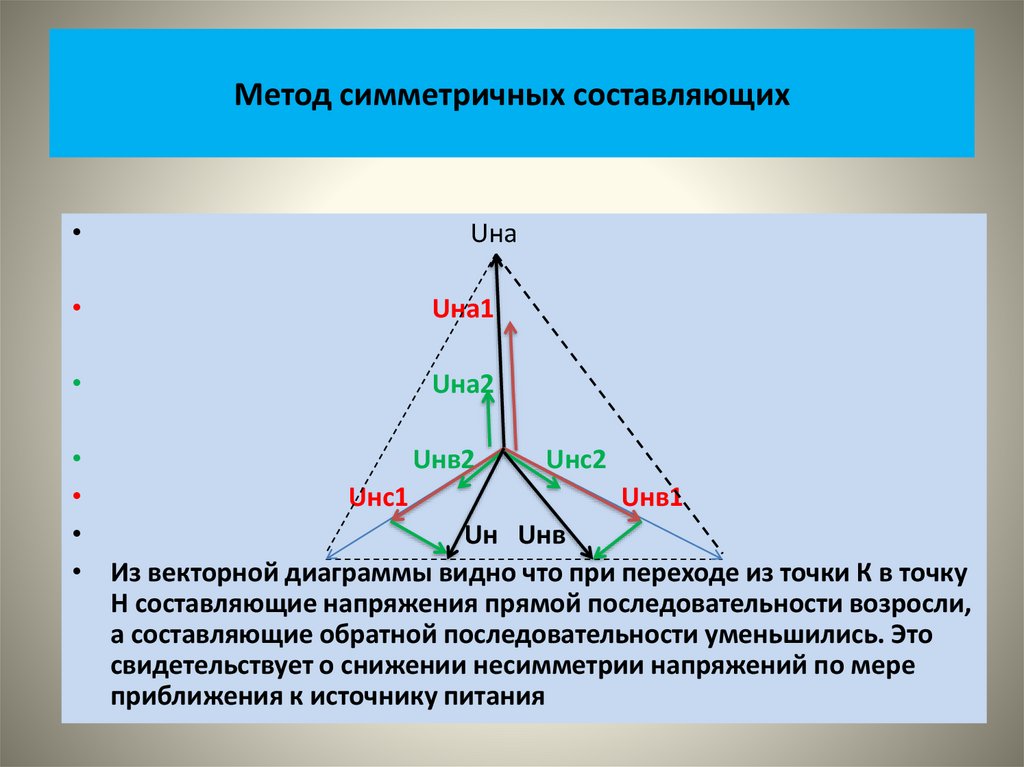





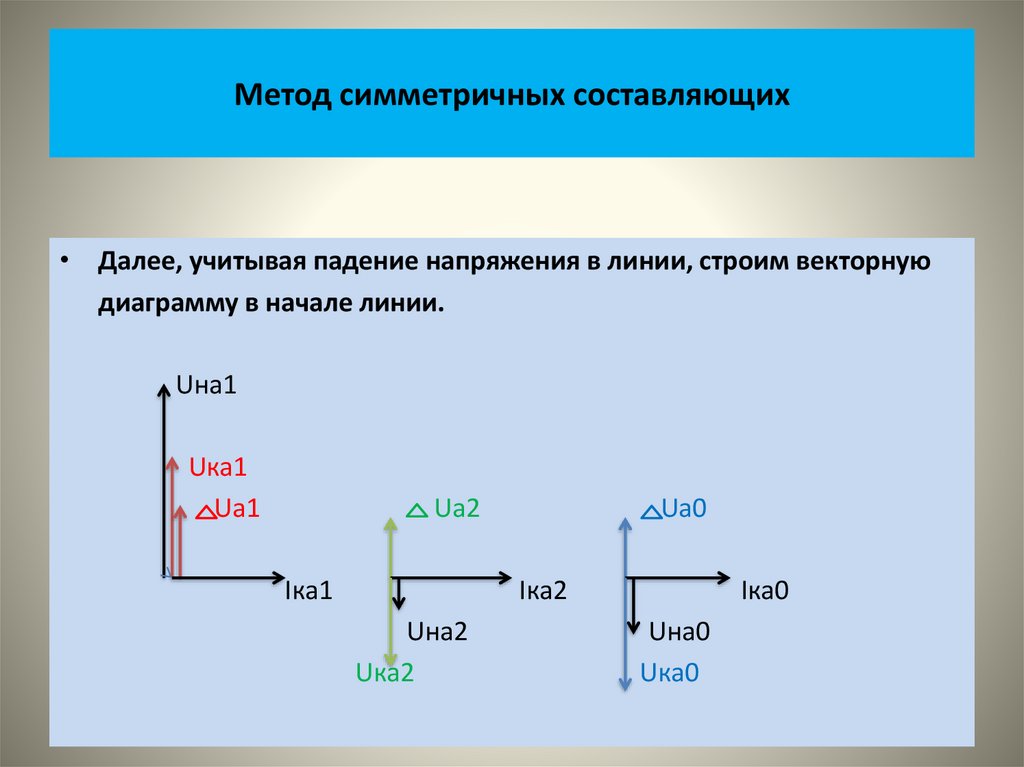




























 Физика
Физика








