Кривые второго порядка гипербола и парабола (1)

1.

Кривые второго порядка: гипербола и парабола
Задание.
1) Составить конспект
• название кривой,
• определение кривой,
• чертеж кривой,
• обозначения осей, полуосей, фокусов,
• определение и формулы эксцентриситета,
• уравнения асимптот.
2) Разобрать номера 1(а) и 2(а) и по аналогии выполнить 1(б) и 2(б).
3) Прикрепить фото выполненного задания.

2.

ГИПЕРБОЛА
Определение. Гиперболой называется множество точек, абсолютная величина разности
расстояний которых до двух данных точек, называемых фокусами, есть величина
постоянная (2а), меньшая, чем расстояние между фокусами (2с).
Простейшее уравнение гиперболы получается, если расположить координатную систему
следующим образом: за ось Ох принять прямую, проходящую через фокусы F1 и F2 , а
y
за ось Оу перпендикуляр в середине отрезка F1F2 .
Тогда уравнение гиперболы примет вид:
B2
x2 y2
2 1,
2
a
b
b
(1)
c
A2 F2
F1
A1
a
2
2
2
0
где b c a
Гипербола имеет две оси симметрии (координатные
оси), с одной из которых (осью абсцисс) она
B1
пересекается в двух точках A1 и A2
называемых вершинами гиперболы. Отрезок A1 A2
длиной 2а называется действительной осью гиперболы, а отрезок B1 B2
длиной 2b – мнимой осью гиперболы. Таким образом, параметры а и b, входящие в
уравнение гиперболы, равны ее полуосям.
Определение. Эксцентриситетом гиперболы называется отношение расстояния между
фокусами к ее действительной оси:
е = с/а
(2)
Очевидно, что е > 1.
x

3.

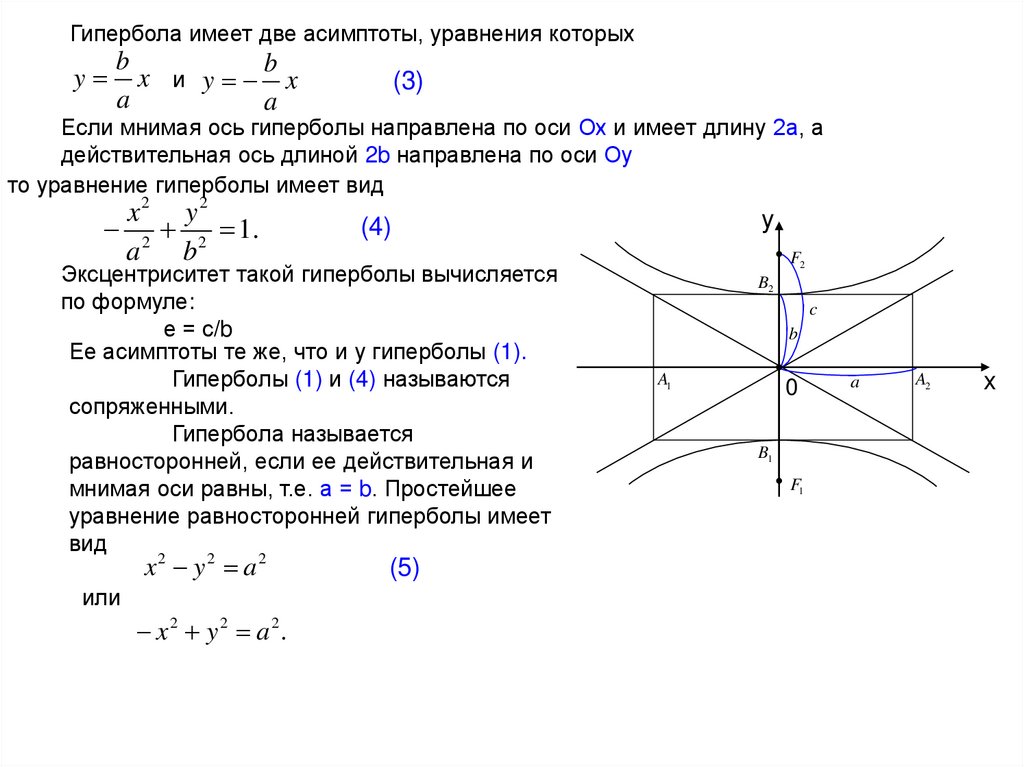
Гипербола имеет две асимптоты, уравнения которых
y
b
b
x и y x
a
a
(3)
Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а
действительная ось длиной 2b направлена по оси Оу
то уравнение гиперболы имеет вид
x2 y2
2 2 1.
a
b
Эксцентриситет такой гиперболы вычисляется
по формуле:
е = с/b
Ее асимптоты те же, что и у гиперболы (1).
Гиперболы (1) и (4) называются
сопряженными.
Гипербола называется
равносторонней, если ее действительная и
мнимая оси равны, т.е. а = b. Простейшее
уравнение равносторонней гиперболы имеет
вид
x2 y 2 a2
или
x2 y 2 a2.
y
(4)
(5)
F2
B2
c
b
A1
0
B1
F1
a
A2
x

4.

Решение.
a) Перенесем свободный член вправо и разделим на него все члены данного
уравнения. В результате получим простейшее уравнение гиперболы:
x2 y2
x2 y2
1, или 2 2 1.
3
4
9 16
Сравнивая это уравнение с уравнением (1), имеем а = 3, b = 4. Таким образом,
действительная ось гиперболы 2а = 6, а мнимая ось 2b = 8; координаты вершин:
A1 ( 3;0) и A2 (3;0).
Далее,
c a 2 b 2 9 16 5;
следовательно, фокусами гиперболы служат точки
F1 ( 5;0)
и
F2 (5;0).
Эксцентриситет гиперболы вычисляем по формуле (2): е = с/а = 5/3. Наконец,
подставляя значения а = 3, b = 4 в формулы (3), получаем уравнения асимптот
гиперболы: у = 4х/3 и у = –4х/3.

5.

ПАРАБОЛА
Параболой называется множество точек, равноудаленных от данной точки,
называемой фокусом, и данной прямой, называемой директрисой параболы.
Величина р, равная расстоянию от фокуса до директрисы, называется
параметром параболы; прямая, проходящая через фокус параболы перпендикулярно
ее директрисе, называется осью, а точка пересечения параболы с ее осью – вершиной
параболы.
Простейшее уравнение параболы получается, если координатная система
расположена следующим образом: за одну из координатных осей берется ось
параболы, а за другую – прямая, перпендикулярная оси параболы и проведенная
посредине между фокусом и директрисой.
y 2 2 px (6)
y 2 2 px (7)
y
y
x
p
x
2
p
F ;0
2
0
p
2
p
F ;0
2
x
0
x 2 2 py (8)
x 2 2 py (9)
y
y
0
p
F 0;
2
x
x
0
y
p
2
y
p
F 0;
2
p
2
x

6.

Уравнение y ax bx c
2
( a 0)
(10)
определяет параболу, ось которой перпендикулярна оси абсцисс.
Аналогично, уравнение
x my 2 ny p
( m 0)
(11)
определяет параболу, ось которой перпендикулярна оси ординат.
Уравнения (10) и (11) приводятся к простейшему виду (6) – (9) путем
тождественных преобразований с последующим параллельным
переносом координатной системы.
Решение.
a) Сравнивая это уравнение с уравнением (6), находим, что
2p = 4, откуда p/2 = 1. Таким образом, точка F(1; 0) – фокус параболы,
а прямая x + 1 = 0 – ее директриса.