https___school.mos.ru_ej_attachments_files_215_559_327_original_8kl-6dz (2)

1.

2.

Система счисления - это знаковая система, в
которой приняты определённые правила записи
чисел.
Число в математике и информатике - это
величина, а не символьная запись.
Цифры – набор символов, участвующих в
записи числа.
Алфавит – совокупность всех цифр,
используемых для записи чисел.
системы счисления
позиционные
непозиционные
352, 23
VII, XIX
величина числа зависит
от номера позиции
цифры при его записи
величина числа не зависит
от номера позиции
цифры при его записи

3.

непозиционные системы счисления
Период палеолита.
10-11 тысяч лет до н.э.
Единичная/
унарная
или
2,5 тысяч лет до н.э.
Древнеегипетская
десятичная
непозиционная система
= 345
- единицы
- десятки
- сотни

4.

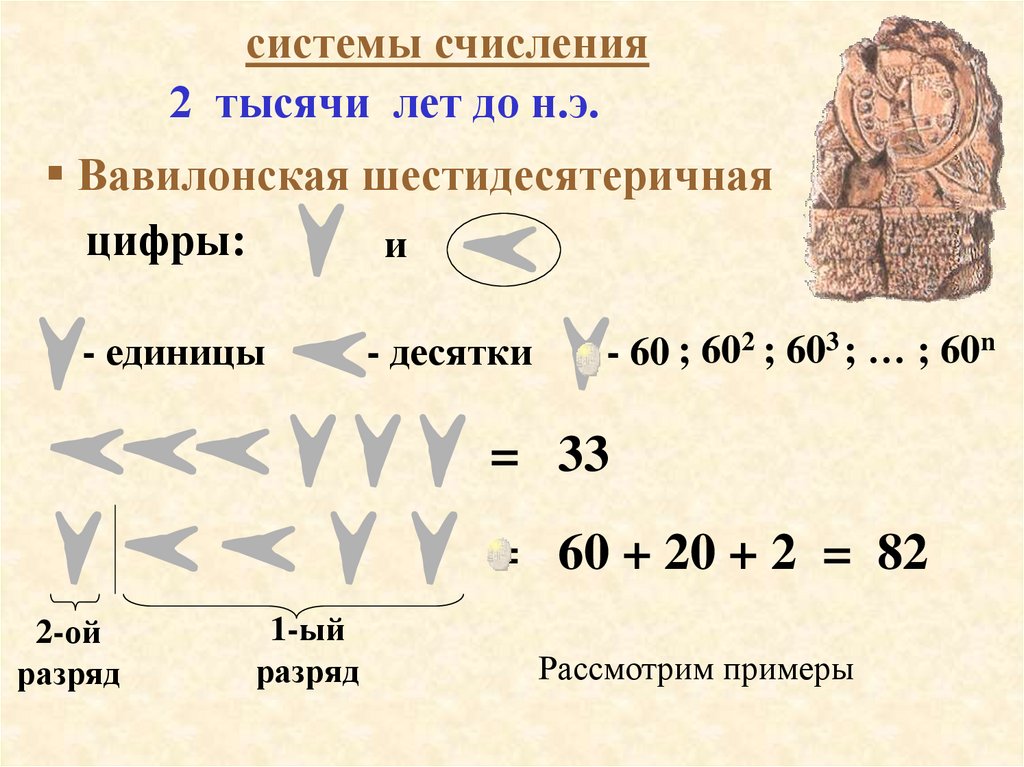
системы счисления
2 тысячи лет до н.э.
Вавилонская шестидесятеричная
цифры:
и
- единицы
- десятки
- 60 ; 602 ; 603 ; … ; 60n
= 33
= 60 + 20 + 2 = 82
2-ой
разряд
1-ый
разряд
Рассмотрим примеры

5.

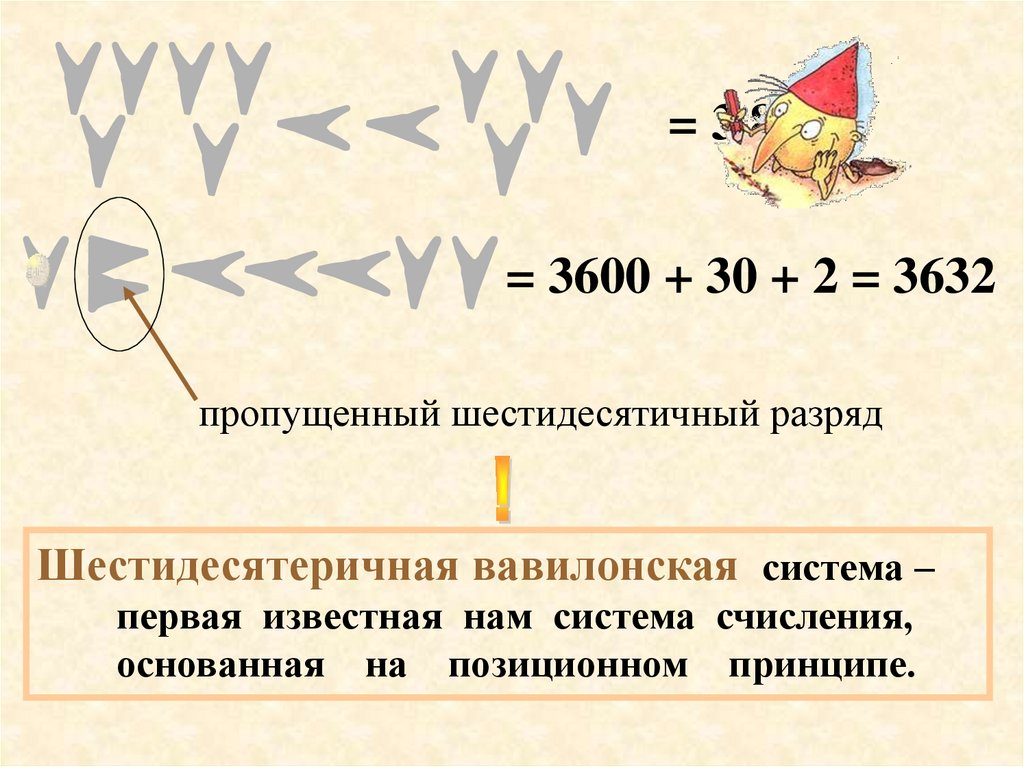
=384
= 3600 + 30 + 2 = 3632
пропущенный шестидесятичный разряд
Шестидесятеричная вавилонская система –
первая известная нам система счисления,
основанная на позиционном принципе.

6.

непозиционные системы счисления
Римская система
500 лет до н.э.
Цифры:
I
V
X
L
C
D
M
1
5
10
50
100
500
1000
Число формировалось из цифр, а также с
помощью групп:
Группа 1-го вида - несколько одинаковых
подряд идущих цифр: XX = 20
Группа 2-го вида - разность значений
двух цифр, если слева стоит меньшая:
СМ = 1000 – 100 = 900
Величина числа суммируется из значений
цифр и групп 1-го или 2-го вида:
X X X I I = 32 D X L I I = 542

7.

I
V
X
L
C
D
M
1
5
10
50
100
500
1000
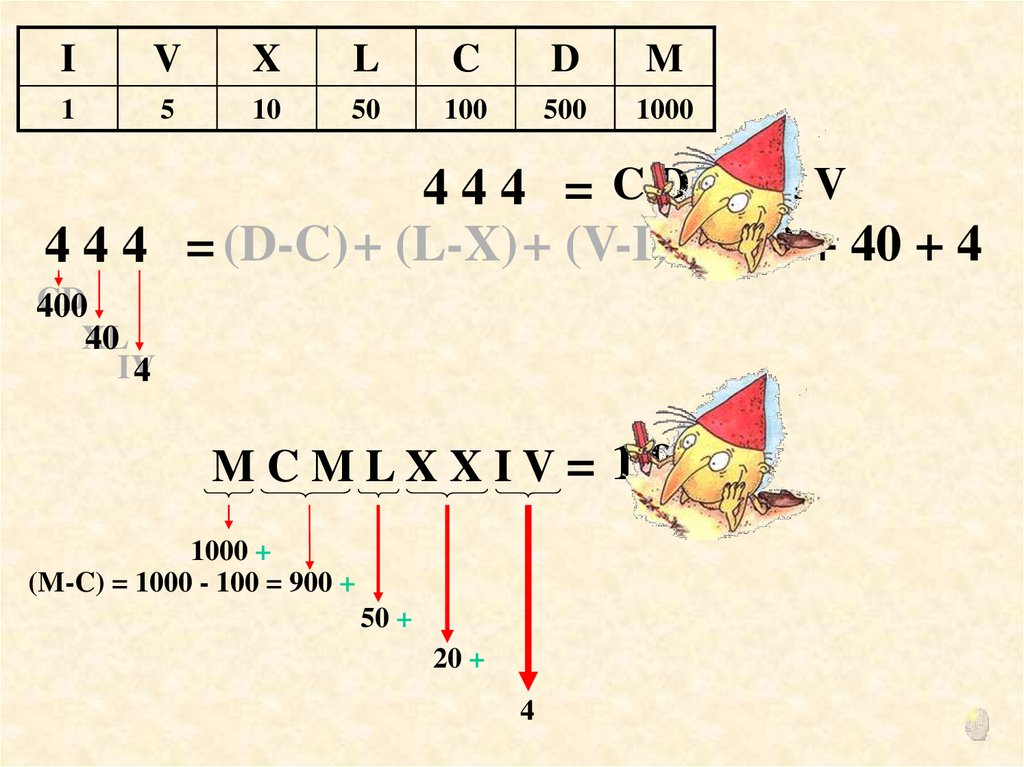
4 4 4 = C D X LIV
4 4 4 = (D-C)+ (L-X)+ (V-I) = 400 + 40 + 4
CD
400
XL
40
IV
4
MCMLXXIV= 1 9 7 4
1000 +
(M-C) = 1000 - 100 = 900 +
50 +
20 +
4

8.

непозиционные системы счисления
Алфавитные системы
1 2 3 4
5 6
7 8 9 10
«Фита»
«Веди»
««Добро»
«Иже»
Земля
«И»»
«Аз»
«Глаголь»
«Есть»
«Зело»
- титло
«… В год 6367. Варяги из заморья
взимали дань…» («Повесть временных лет»)
- тысячи
- тьма: х10 000
= 10 000
100 000 - легион
1000 .000
. . - леодр
1050 - колода
«более сего несть человеческому уму разумевати»

9.

позиционные системы счисления
(запись чисел строится по разрядам)
Основание – количество цифр в системе счисления
1. Заполним таблицу
Название системы сч.
Десятичная
Двоичная
Пятеричная
Восьмеричная
Шестнадцатеричная
Основание
10
2
5
8
16
Алфавит
{0,1,2,3,4,5,6,7,8,9}
{0,1}
{0, 1, 2,3,4}
{0,1,2,3,4,5,6,7}
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,
В, С, D, E, F}
2. Рассмотрим примеры чисел в различных системах
счисления: 3045; 101102; 3А016; 56710; 12223
3. Записали свои примеры чисел

10.

позиционные системы счисления
(запись чисел строится по разрядам)
Основание – количество цифр в системе счисления
Свёрнутая и развёрнутая формы записи числа
Рассмотрим примеры записей чисел в различных системах
счисления в свёрнутой форме:
567810, 1245; 101102; 5С016; 12223
Развёрнутая запись – сумма произведений цифр
числа на основание, возведённое в целую степень
(представление числа по разрядам)
Запишем числа в развёрнутой форме:
567810, 1245; 101102; 5С016; 12223
С помощью развёрнутой формы записи числа можно
перевести число в десятичную систему счисления

11.

Домашняя работа
1.
2.
3.
4.
Выучить основные понятия темы (понятие системы счисления,
цифры, алфавита, знать цифры алфавита римской системы счисления и
правила составления римского числа, понятие основания позиционной
системы счисления, свёрнутой и развёрнутой формы записи числа,
уметь приводить примеры систем счисления и знать их алфавиты).
Записать римскими цифрами следующие десятичные числа: 569, 4590,
888, 9991, 1745, 599.
Записать десятичными цифрами CCLIX, MDXLII, CMXCIX, CMLXIV
и MCMXCVII
Записать следующие числа в развёрнутой форме: А30416, ВС1416, 10108
(переводить в десятичную систему счисления числа не нужно).