fc887f507ca5f39dffe11cb1fccf1861

1. Математические и инструментальные методы принятия решений

Граецкая Оксана Владимировна, к.т.н., доцент
кафедры Системного анализа и управления
Чусова Юлия Сергеевна, старший преподаватель
кафедры Системного анализа и управления

2. Цели и задачи дисциплины

Цели освоения дисциплины «Математические и инструментальные методы принятия
решений» является формирование профессионально ориентированных компетенций,
позволяющих на современном научно-техническом уровне выполнять системный
анализ исследуемых объектов, реализовывать эффективные решения практикоориентированных учебных, научно-исследовательских наукоемких профессиональных
задач принятия решений.
Задачи:
- формирование у обучаемых целостного представления об объектах и субъектах
системного анализа, методах, средствах и особенностях их применения к решению
задач принятия решений;
- освоение обучаемым контингентом знаний, умений и навыков приложения
технологий системного анализа и принятия решений во всех сферах
профессиональной деятельности, а также создание необходимых предпосылок для
наилучшего усвоения связных циклов дисциплин образовательного направления;
- формирование у обучающихся способности к самообразованию, самостоятельному
повышению
квалификации
и
профессионализма
в
рассматриваемом
дисциплинарном направлении.
2

3. Содержание дисциплины

1. Введение в принятие решений.
2. Введение в методы оптимизации.
3. Модели
и
методы
линейного
программирования.
4. Модели и методы целочисленного линейного
программирования.
5. Нелинейное программирование. Численные
методы нелинейного программирования.
6. Оптимизация на графах.
7. Динамическое программирование.
8. Методы безусловной оптимизации.
9. Методы многокритериальной оптимизации.
3

4. Виды работ по дисциплине

1. Решение практических задач и выполнение
заданий на практических занятиях.
2. Выполнение и защита лабораторных работ.
3. Контрольная работа.
4. Тестирование.
4

5. Процесс принятия решений

Под принятием решений понимается особый процесс
человеческой деятельности, направленный на выбор
наилучшего варианта действий.
Этот
выбор
может
осуществляться
лицом,
принимающим решение (ЛПР), как на основе опыта и
интуиции, так и с помощью математических и
инструментальных методов и средств, повышающих
эффективность и обоснованность выбора. Кроме того,
принятие
решений
с
использованием
специализированных информационных систем – систем
поддержки принятия решений (СППР) позволяет сочетать
субъективные предпочтения ЛПР с компьютерным
анализом ситуаций в условиях многоваpиантности,
5
многокритериальности, неопределенности и риска.

6. Процесс принятия решений

Процесс, в ходе которого человек выбирает между двумя или более
доступными альтернативными путями (вариантами действий) для
достижения поставленной цели (целей), называется принятием
решений.
Чтобы избежать серьезных последствий необоснованных решений, ЛПР
выбирают математические инструменты, представляющие собой набор
количественных методов для детального анализа проблемы и поиска
оптимальных или удовлетворительных решений.
Принятие решений имеет жизненно важное значение для всей
управленческой деятельности при определении целей, разработки
проектов, формировании организационной структуры, мотивации
персонала, а также внедрении инноваций.
Принятие эффективных решений связано с проблемой выбора методов и
средств поиска лучшего решения, позволяющего достигать желаемых
целей.
6

7. Классификация задач принятия решений

I) Все задачи, связанные с принятием решений, в зависимости от
возможностей математического описания (формализации) можно
разделить на следующие виды:
• хорошо структурированные задачи – могут быть выражены
формально (т.е. в виде уравнений, неравенств и т.д.). Такие задачи
могут решаться на основе математических методов, например,
методов математического программирования;
• неструктурированные задачи – описываются только на
содержательном уровне (в словесной форме) и решаются на основе
неформальных процедур. Для решения таких задач часто
используются методы экспертного анализа (экспертных оценок);
• слабоструктурированные задачи – содержат как количественные,
так и качественные элементы. К ним относят многокритериальные
задачи, задачи принятия решений в условиях риска, с участием
нескольких заинтересованных сторон и т.д. Эти задачи решаются на
основе сочетания формальных и неформальных процедур (методов
системного анализа).
7

8. Классификация задач принятия решений

II) По типам решения:
• повторяющиеся решения принимаются очень часто и не требуют
тщательного анализа и оценки каждый раз. Сотрудники на более
низком уровне иерархии уполномочены принимать эти решения
самостоятельно, поскольку для решения таких проблем
используется стандартная процедура;
• уникальные (неповторяющиеся) решения принимаются время от
времени, они являются нерегулярными. Решение подобных проблем
может быть различной степени сложности. Сложные проблемы
решаются верхними уровнями управления, в то время как
несложные проблемы решаются низшим руководством.
III) По учету времени:
• статические;
• динамические.
IV) По характеру исходных данных:
• в условиях определенности;
• в условиях неопределенности (в условиях риска и противодействия
8
ему).

9. Классификация задач принятия решений

V) По способам формирования множества альтернатив:
• с фиксированным (заданным, заранее установленным) набором
(множеством, совокупностью) вариантов решений (альтернатив,
стратегий);
• с формируемым набором альтернатив в процессе принятия
решений.
VI) По количеству критериев:
• с одним критерием (показателем качества, эффективности, целевой
функцией, однопараметрические);
• с множеством критериев (многопараметрические).
VII) По количеству участников процесса принятия решений:
• принятия индивидуальных решений (на основе суждения одного
эксперта или лица, принимающего решение);
• принятия коллективных решений (на основе суждения группы
9
лиц, принимающих решение).

10. Типы задач выбора

Цели и результаты принятия решений могут быть
различны, на основе этого формируются
основные типы задач выбора:
• выбор
единственного
наилучшего
(оптимального) варианта;
• выбор
нескольких
лучших
вариантов,
ранжирование вариантов;
• кластеризация альтернатив.
10

11. Классификация методов принятия решений

Специфика
задач
принятия
решений
обосновывает разнообразие методов принятия
решений. В настоящее время все методы
принятия решений можно разделить на три
группы:
1) неформальные методы принятия решений;
2) коллективные методы обсуждения и принятия
решений;
3) количественные методы принятия решений.
11

12. Введение в методы оптимизации

Оптимизация
–
целенаправленная
деятельность,
заключающаяся в получении наилучших результатов при
соответствующих условиях.
Оптимизация – поиск наилучшего варианта при наличии
множества альтернативных.
Оптимизация (в математике, информатике и исследовании
операций) – задача нахождения экстремума (минимума или
максимума) целевой функции в некоторой области
конечномерного векторного пространства, ограниченной
набором линейных и/или нелинейных равенств и/или
неравенств.
12

13. Требования при постановке задачи оптимизации

При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При
этом формулировка каждой задачи оптимизации должна
требовать экстремального значения лишь одной величины,
то есть одновременно системе не должно приписываться
два и более критерия оптимизации, так как практически
всегда экстремум одного критерия не соответствует
экстремуму другого.
2. Наличие ресурсов оптимизации, под которыми понимают
возможность выбора значений некоторых параметров
оптимизируемого объекта. Объект должен обладать
определенными степенями свободы – управляющими
воздействиями.
3. Возможность количественной оценки оптимизируемой
величины, поскольку только в этом случае можно
сравнивать эффекты от выбора тех или иных управляющих
воздействий.
4. Учет ограничений.
13

14. Критерий оптимальности

Критерием оптимальности называется количественная
оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности
составляется целевая функция, представляющая собой
зависимость критерия оптимальности от параметров,
влияющих на ее значение. Вид критерия оптимальности
или целевой функции определяется конкретной задачей
оптимизации. Таким образом, задача оптимизации
сводится к нахождению экстремума целевой функции.
Требования к критерию оптимальности:
• должен выражаться количественно;
• должен быть единственным;
• должен отражать наиболее существенные стороны
процесса;
• желательно,
чтобы
имел
ясный
физический
(экономический) смысл и легко рассчитывался.
14

15. Классификация методов оптимизации

Общая формулировка задач оптимизации задаёт большое разнообразие их
классов. От класса задачи зависит подбор метода (эффективность её
решения).
Классификацию задач определяют: целевая функция и допустимая область
(задаётся системой неравенств и равенств или более сложным алгоритмом).
1. Методы оптимизации классифицируют в соответствии со способом
поиска:
• Локальные методы: сходятся к какому-нибудь локальному экстремуму
целевой функции. В случае унимодальной целевой функции, этот
экстремум единственен, и будет глобальным максимумом/минимумом.
• Глобальные методы: имеют дело с многоэкстремальными целевыми
функциями. При глобальном поиске основной задачей является
выявление тенденций глобального поведения целевой функции.
2. Существующие в настоящее время методы поиска можно разбить на три
большие группы:
• детерминированные;
• случайные (стохастические);
• комбинированные.
15

16. Классификация методов оптимизации

3. По критерию размерности допустимого множества методы
оптимизации делят на:
• методы одномерной оптимизации;
• методы многомерной оптимизации.
4. По требованиям к гладкости и наличию у целевой функции
частных производных, методы можно разделить на:
• прямые методы, требующие только вычислений целевой функции
в точках приближений;
• методы первого порядка: требуют вычисления первых частных
производных функции;
• методы второго порядка: требуют вычисления вторых частных
производных, то есть гессиана целевой функции.
5. Оптимизационные методы по типу метода делятся на следующие
группы:
• аналитические методы (например, метод множителей Лагранжа и
условия Каруша — Куна — Таккера);
• численные методы;
• графические методы.
16

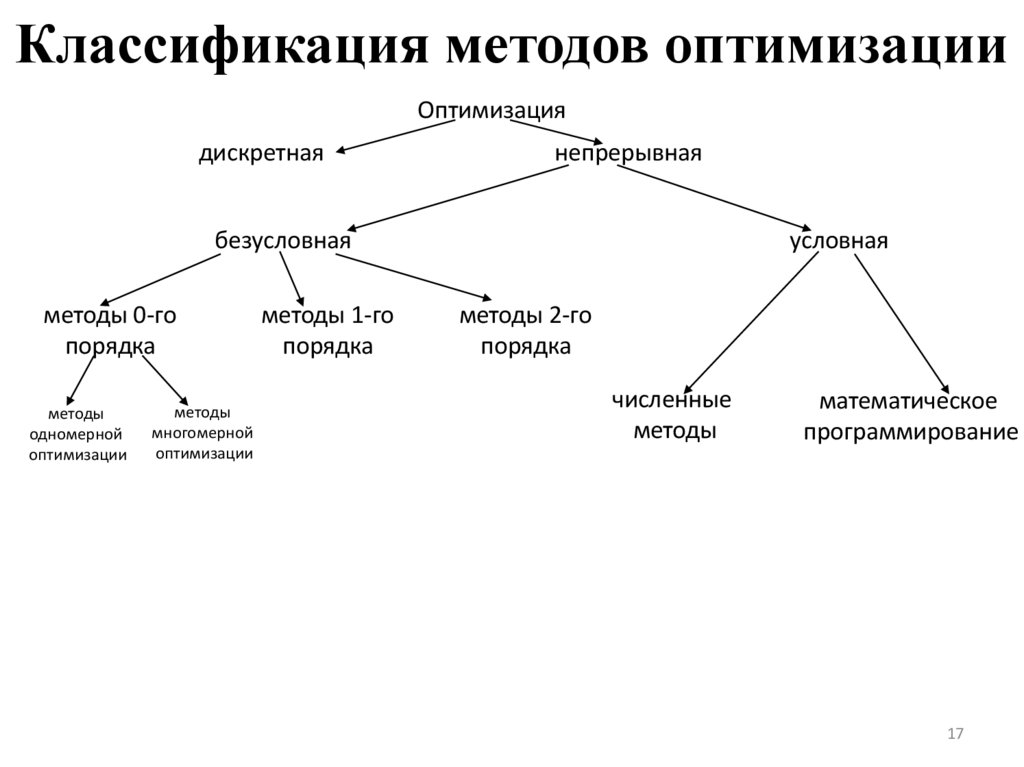
17. Классификация методов оптимизации

Оптимизация
дискретная
непрерывная
безусловная
методы 0-го
порядка
методы
одномерной
оптимизации
методы
многомерной
оптимизации
методы 1-го
порядка
условная
методы 2-го
порядка
численные
методы
математическое
программирование
17

18. Построение математической модели

Процесс построения математической модели можно
начинать с ответов на 3 следующих вопроса:
1. Для определения каких величин должна быть
построена модель? Т.е. как идентифицировать
переменные (искомые величины, неизвестные)
задачи?
2. Какие ограничения должны быть наложены на
переменные, чтобы выполнялись условия,
характерные для моделируемой системы?
3. В чем состоит цель, для достижения которой из
всех допустимых значений переменных нужно
выбрать те, которые будут соответствовать
оптимальному (наилучшему) решению задачи?
18

19. Постановка задачи оптимизации

Компоненты оптимизационной задачи:
1. Целевая функция: F(X) Rn, X=(x1,х2, … хn)
2. Ограничения в виде равенств или неравенств:
gi(X)≥0
3. Область допустимых значений (решений):
X D ⊂ Rn
В
общем
виде
задача
оптимизации
(математического программирования):
F(X)→min
gi(X)≥0, i=1..J
X D ⊂ Rn
19

20. Классификация задач математического программирования

В зависимости от природы множества X задачи математического
программирования классифицируются как:
• задачи дискретного программирования (или комбинаторной
оптимизации) — если X конечно или счётно;
• задачи целочисленного программирования — если X является
подмножеством множества целых чисел;
• задачи нелинейного программирования, если ограничения или
целевая функция содержат нелинейные функции и X является
подмножеством конечномерного векторного пространства;
• задачи линейного программирования — если все ограничения и
целевая функция содержат лишь линейные функции.
Кроме того, разделами математического программирования являются
параметрическое программирование, динамическое программирование и
стохастическое программирование.
Способ нахождения экстремума полностью определяется классом
задачи.
Математическое программирование используется при решении
оптимизационных задач исследования операций.
20

21. Исследование операций

Исследование операций — научная дисциплина,
занимающаяся разработкой и практическим применением
методов наиболее эффективного управления различными
организационными системами.
Цель исследования операций — количественное
обоснование принимаемых решений по организации
управления.
При решении конкретной задачи управления применение
методов исследования операций предполагает:
• построение экономических и математических моделей
для задач принятия решения в сложных ситуациях или в
условиях неопределенности;
• изучение взаимосвязей, определяющих впоследствии
принятие
решений,
и
установление
критериев
эффективности, позволяющих оценивать преимущество
того или иного варианта действия.
21

22. Исследование операций

Операция — любое управляемое мероприятие, направленное на
достижение цели. Результат операции зависит от способа ее проведения,
организации, иначе — от выбора некоторых параметров.
Всякий определенный выбор параметров называется решением.
Оптимальными считают те решения, которые по тем или иным
соображениям предпочтительнее других. Поэтому основной задачей
исследования операций является предварительное количественное
обоснование оптимальных решений.
Для применения количественных методов исследования требуется
построить математическую модель операции. При построении модели
операция, как правило, упрощается, схематизируется и схема операции
описывается с помощью того или иного математического аппарата.
Модель операции — это достаточно точное описание операции с
помощью математического аппарата (различного рода функций,
уравнений, систем уравнений и неравенств и т.п.). Составление модели
операции требует понимания сущности описываемого явления и знания
математического аппарата.
Эффективность операции — степень ее приспособленности к
выполнению задачи — количественно выражается в виде критерия
эффективности (целевой функции).
22

23. Классификация задач исследования операций

Все модели исследования операций могут быть классифицированы в
зависимости от природы и свойств операции, характера решаемых задач,
особенностей применяемых математических методов.
Оптимизационные задачи возникают при попытке оптимизировать
планирование и управление сложными системами, в первую очередь
экономическими системами.
Задачи сетевого планирования и управления рассматривают соотношения
между сроками окончания крупного комплекса операций (работ) и моментами
начала всех операций комплекса. Эти задачи состоят в нахождении
минимальных продолжительностей комплекса операций, оптимального
соотношения величин стоимости и сроков их выполнения.
Задачи массового обслуживания посвящены изучению и анализу систем
обслуживания с очередями заявок или требований и состоят в определении
показателей эффективности работы систем, их оптимальных характеристик,
например, в определении числа каналов обслуживания, времени обслуживания
и т.п.
Задачи управления запасами состоят в отыскании оптимальных значений
уровня запасов и размера заказа.
Задачи распределения ресурсов возникают при определенном наборе операций
(работ), которые необходимо выполнять при ограниченных наличных ресурсах,
и требуется найти оптимальные распределения ресурсов между операциями
или состав операций.
23

24. Классификация задач исследования операций

Задачи ремонта и замены оборудования актуальны в связи с износом и
старением оборудования и необходимостью его замены с течением
времени. Задачи сводятся к определению оптимальных сроков, числа
профилактических ремонтов и проверок, а также моментов замены
оборудования модернизированным.
Задачи составления расписания (календарного планирования) состоят в
определении оптимальной очередности выполнения операций
(например, обработки деталей) на различных видах оборудования.
Задачи планировки и размещения состоят в определении оптимального
числа и места размещения новых объектов с учетом их взаимодействия с
существующими объектами и между собой.
Задачи выбора маршрута, или сетевые задачи, чаще всего встречаются
при исследовании разнообразных задач на транспорте и в системе связи
и состоят в определении наиболее экономичных маршрутов.
Задачи теории игр - принятие оптимальных решений в конфликтных
ситуациях. В них необходимо выработать рекомендации по разумному
поведению участников конфликта, определить их оптимальные
стратегии.
Многокритериальные задачи исследования операции помогают
отбросить заведомо неудачные варианты решений.
24