Осевая симметрия геометрии

1.

Геометрия: Осевая
Симметрия
Симметрия в геометрии описывает свойство фигуры оставаться
неизменной при определённых преобразованиях. Осевая
симметрия, одна из её форм, характеризуется наличием прямой
линии, называемой осью симметрии. При отражении относительно
этой оси фигура полностью совпадает с исходной, как будто её
сложили пополам.

2.

Что такое симметрия?
Симметрия, в самом широком смысле, означает
гармонию, пропорциональность и баланс, которые
можно обнаружить в природе, искусстве и науке. В
математике симметрия является фундаментальным
понятием, описывающим свойства объектов, которые
остаются неизменными под действием определённых
преобразований, таких как отражение, вращение или
сдвиг.
Осевая симметрия, или зеркальная симметрия,
возникает, когда фигура может быть разделена прямой
линией на две зеркальные половины, которые идеально
совпадают при накладывании друг на друга. Эта линия
называется осью симметрии, и она играет ключевую
роль в понимании структуры и свойств геометрических
объектов.

3.

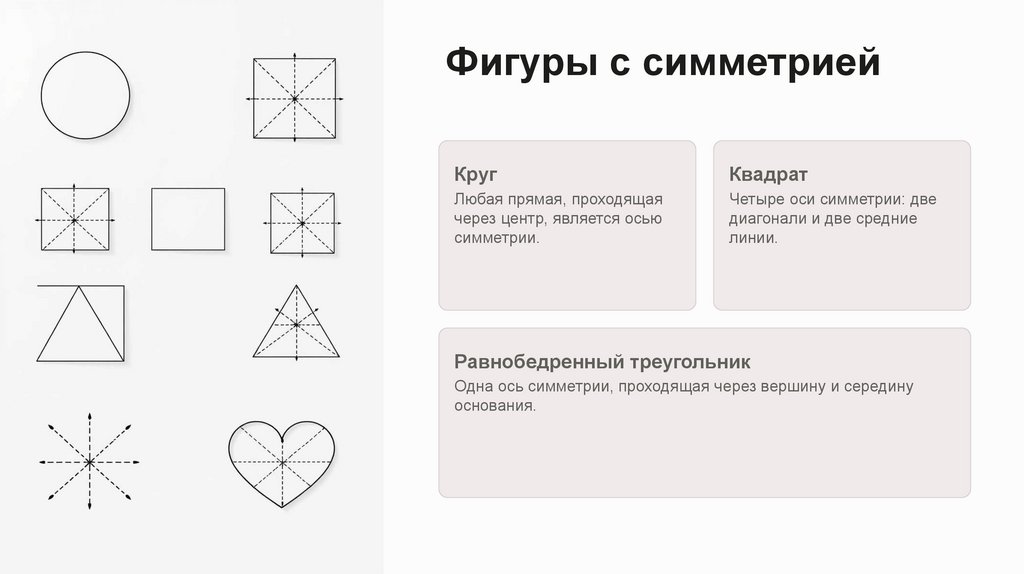
Фигуры с симметрией
Круг
Квадрат
Любая прямая, проходящая
через центр, является осью
симметрии.
Четыре оси симметрии: две
диагонали и две средние
линии.
Равнобедренный треугольник
Одна ось симметрии, проходящая через вершину и середину
основания.

4.

Примеры в природе
1
2
3
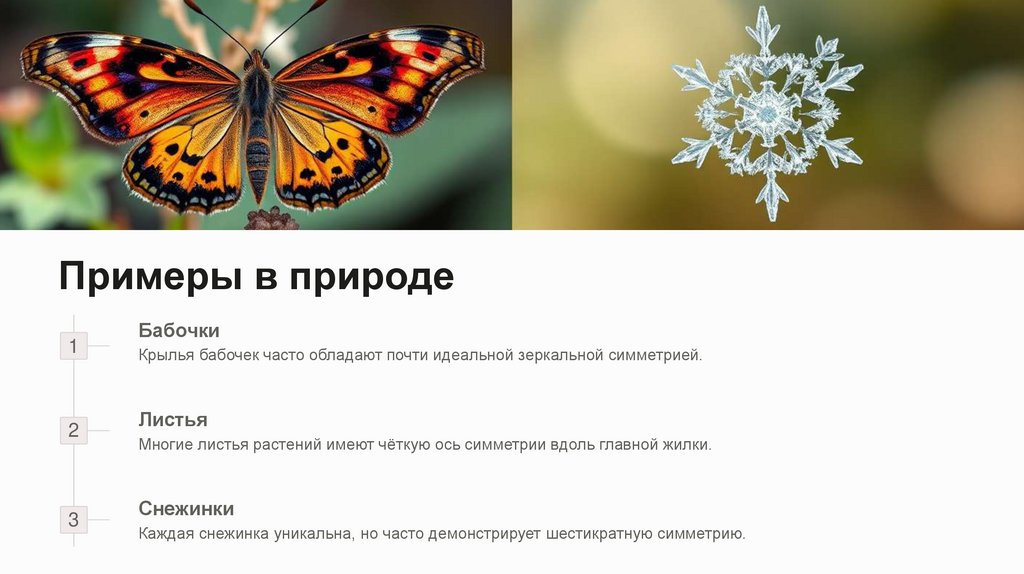
Бабочки
Крылья бабочек часто обладают почти идеальной зеркальной симметрией.
Листья
Многие листья растений имеют чёткую ось симметрии вдоль главной жилки.
Снежинки
Каждая снежинка уникальна, но часто демонстрирует шестикратную симметрию.

5.

Симметрия
1
2
3
Архитектура
Здания часто проектируются с осевой симметрией для
создания гармонии.
Искусство
Композиция картин и скульптур часто строится на принципах
симметрии.
Дизайн
Предметы быта и техники нередко имеют симметричную
форму.

6.

Как найти ось симметрии?
1
Метод
Вообразите, что фигуру можно сложить пополам.
Свойство
2
Точки одной половины фигуры должны совпадать с точками другой
половины.
Проверка
3
Отражение фигуры относительно линии должно
давать ту же фигуру.

7.

Итоги по теме
Осевая симметрия является важным геометрическим свойством,
проявляющимся как в абстрактных фигурах, так и в реальном мире.
Понимание принципов симметрии помогает нам лучше
анализировать формы, создавать гармоничные объекты и ценить
красоту порядка в природе и искусстве.