02_UPg_Uvod_do_programovani

1. Úvod do programování 2. hodina

doc. RNDr. Jan Lánský, Ph.D.
Katedra informatiky a matematiky
Fakulta ekonomických studií
Vysoká škola finanční a správní
2015

2. Umíme z minulé hodiny

Obecné informace o předmětu
Ukázka: postup řešení problému v přirozeném
jazyce a jeho převod do C#
Instalace C#, vytvoření projektu, spuštění
programu
Syntax C#
Proměnné
Přiřazení, aritmetické operátory (zbytek po
celočíselném dělení), výpis na obrazovku
Porovnací operátory, podmíněný příkaz (se
zápornou větví, vnořený)
Jan Lánský
Úvod do programování 2. hodina
2

3. Cíle hodiny

Syntax
V C# existuje
cyklus foreach,
ten nebudeme
probírat. Mnoho
jiných jazyků
nemá ekvivalent
Složený příkaz
Logické operátory
Čtení vstupu z klávesnice
Cykly while a for (continue, break), vnořené cykly
Algoritmy
Prohození hodnot dvou proměnných
Ciferný součet, Euklidův algoritmus
Prvočíselný rozklad, test prvočíselnosti
Základy časové složitosti algoritmů
Jan Lánský
Úvod do programování 2. hodina
3

4. Prohození hodnot dvou proměnných

V x bude hodnota, která byla
původně v y.
V y bude hodnota, která byla
původně v x.
Nejde prohodit atomicky
x=5
y=3
tmp =3
Jan Lánský
tj. jen za jedno použití operátoru
Pomocná proměnná tmp, která
uchovává hodnotu x
Úvod do programování 2. hodina
4

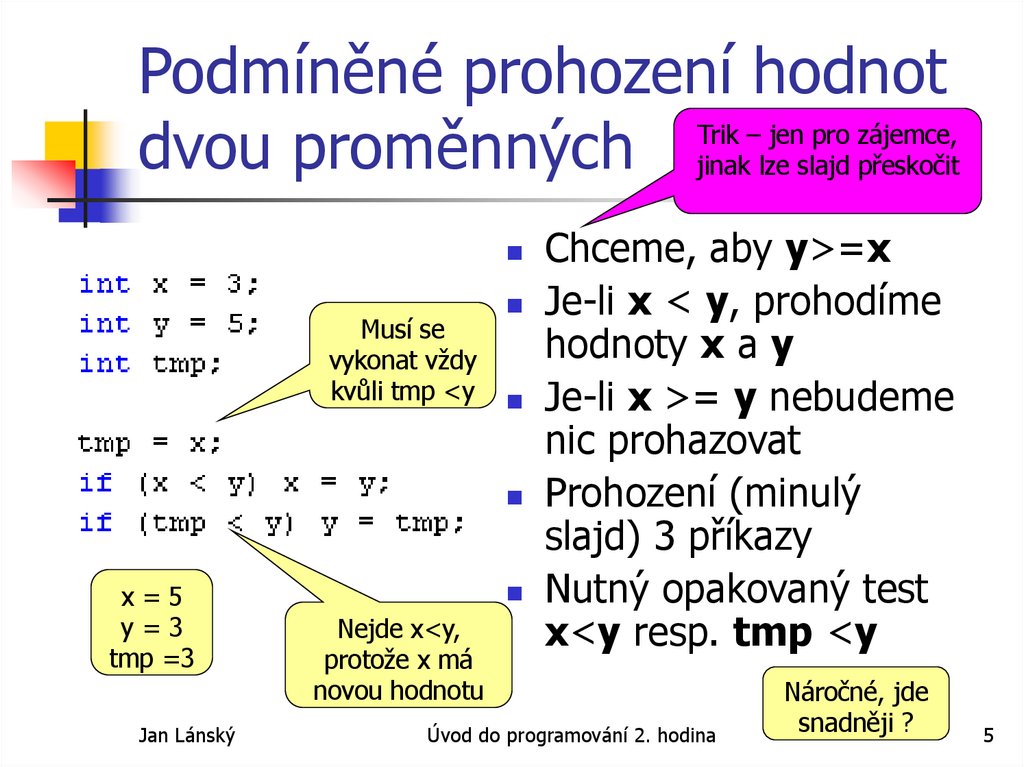
5. Podmíněné prohození hodnot dvou proměnných

Podmíněné prohození hodnot
Trik – jen pro zájemce,
dvou proměnných jinak lze slajd přeskočit
Chceme, aby y>=x
Je-li x < y, prohodíme
hodnoty x a y
Je-li x >= y nebudeme
nic prohazovat
Prohození (minulý
slajd) 3 příkazy
Nutný opakovaný test
x<y resp. tmp <y
Musí se
vykonat vždy
kvůli tmp <y
x=5
y=3
tmp =3
Jan Lánský
Nejde x<y,
protože x má
novou hodnotu
Úvod do programování 2. hodina
Náročné, jde
snadněji ?
5

6. Složený příkaz

Blok po sobě následujících příkazů, který je
považován za jeden příkaz
Příkazy uzavřeny ve složených závorkách
{ (alt + 123), } (alt + 125)
Využití
V podmíněném příkazu (nebo v cyklu)
Ve vnořeném podmíněném příkazu
Místo jednoho příkazu se vykoná složený příkaz
obsahující několik příkazů
Jan Lánský
Úvod do programování 2. hodina
6

7. Podmíněné prohození hodnot pomocí složeného příkazu

Chceme, aby x >= y
Je-li x < y, prohodíme
hodnoty x a y
Je-li x >= y nebudeme
nic prohazovat
Jedna podmínka x < y
následovaná složeným
příkazem provádějícím
prohození
začátek
konec
Jan Lánský
x=5
y=3
tmp =3
Úvod do programování 2. hodina
7

8. Dvojitě zanořený podmíněný příkaz – vynechání else větve

Chyba: else patří k vnitřnímu if
Správně: složeným příkazem jsme určili, že vnitřní if nemá else
Jan Lánský
Úvod do programování 2. hodina
8

9. Logické operátory

operandy typu bool
nejčastěji výsledek porovnávacích operátorů.
&& Logické AND (alt + 38)
|| logické OR (alt + 124)
Infixní binární operátory
Levý operand [logický operátor] pravý operand
! Logická negace
Unární prefixní operátor (! operand)
Využítí
V podmíněném příkazu (a v cyklu)
Jan Lánský
Úvod do programování 2. hodina
9

10. Interval

Porovnávací operátory se vykonají dříve než
logické operátory, závorky nejsou nutné, ale
nevadí pokud je chceme psát
Syntaktická chyba
První porovnání: 0 < a vrací bool
Druhé porovnání: nekompatibilní operandy
Jan Lánský
Úvod do programování 2. hodina
10

11. Logické operátory

Jan Lánský
Úvod do programování 2. hodina
11

12. XOR na 3 způsoby

funkce XOR = eXclusive OR
true pro 01 nebo 10 (různé)
false pro 00 a 11 (shodné)
Jde to i jednodušeji
Závorky navíc nevadí
Pokud si nejsme jisti
Pomocí operátoru nerovnosti
Jan Lánský
Úvod do programování 2. hodina
12

13. Zkrácené vyhodnocování

Je-li o výsledku logického výrazu
rozhodnuto po vyhodnocení jeho části,
zbytek výrazu se nevyhodnocuje
Je-li nesplněn levý operand &&
nevyhodnocuje se pravý
Nedojde k
dělení nulou
Př.: (a != 0) && (x / a > y)
Je-li splněn levý operand || nevyhodnocuje
se pravý
Jan Lánský
Úvod do programování 2. hodina
13

14. Vstup z klávesnice

Pro uživatele programu příjemnější
vstup z klávesnice než změna hodnota
ve zdrojovém kódu a kompilace
Pokud by to uživatelé vůbec zvládli …
Při ladění programu vstup z klávesnice
nahradit pevnými hodnotami
Ruční zadávání hodnot je ztráta času
Jan Lánský
Úvod do programování 2. hodina
14

15. Vstup z klávesnice

s = Console.ReadLine();
x = Convert.ToInt32(s);
Návratová hodnota řetězec string s
Vstupní řetězec string převede na celé číslo int x
x = Convert.ToInt32(Console.ReadLine());
Lze volat i vnořeně
Není třeba pomocná proměnná
Jan Lánský
Úvod do programování 2. hodina
15

16. Vstup z klávesnice

Uživateli oznámíme, co chceme zadat
Načtení řetězce a převod na celé
číslo
V jednom
příkazu
Výsledky uložit do x a y
Jan Lánský
Úvod do programování 2. hodina
16

17. Cyklus while

Existuje varianta do příkaz while ()
Nebudeme probírat
Cyklus while
Hlavička cyklu
Tělo cyklu
Syntax: while (podmínka) příkaz;
Dokud je splněna podmínka opakuj vykonávání (složeného)
příkazu
Podmínka musí být v závorce a její hodnota musí být datového typu
bool
Srovnej: podmíněný příkaz opakuj max 1x
Obvykle
Dopředu nevíme počet opakování
chyba
Neprovede se ani jednou – Př.: while (0>1)
Nekonečno opakování – Př.: while (true)
Nekonečný cyklus program nikdy neskončí musíme program zabít
1. krok – Podmínka: true (krok 2), false (konec)
2. krok – Příkaz
3. krok – Přejít na krok 1
Jan Lánský
Úvod do programování 2. hodina
17

18. Ciferný součet

Pracuje s y, kopii x, aby x se zachovalo
Do cif přičteme poslední cifru čísla y
Odstraníme poslední cifru čísla y
Jan Lánský
Úvod do programování 2. hodina
18

19. Euklidův algoritmus - princip

Nejstarší algoritmus na
světě (300 př. n. l.)
Euklidův algoritmus - princip
Spočte největšího společného dělitele d dvou čísel m a
n. NSD(m,n) = d
d dělí m (značení d | m) pokud k1 Z: m = k1 * d
NSD(m,n) = Max d { d | m a zároveň d | n }
Př.: NSD(490, 75) = 5
Odvození algoritmu:
d|n
n%d=0
Pokud d | m a zároveň d | n poté d | (m – k * n), kde k Z
m = k1 * d; n = k2 * d;
m – k * n = (k1 * d) – k * (k2 * d) = (k1 – k * k2 ) * d
NSD(m,n) = NSD(m-k*n,n), kde k je celé
NSD(m,n) = n, pokud n | m
Jan Lánský
Konečnost
algoritmu
Úvod do programování 2. hodina
19

20. Euklidův algoritmus - příklad

1. krok
NSD(490, 75)
490 = 6*75 + 40
490 % 75 = 40
NSD(40, 35)
40 = 1*35 + 5
40 % 35 = 5
2. krok
NSD (75, 40)
75 = 1*40 + 35
75 % 40 = 35
3. krok
4. krok
NSD (35, 5)
35 = 7*5 + 0
35 % 5 = 0
STOP: n | m
Jan Lánský
Úvod do programování 2. hodina
20

21. Euklidův algoritmus – I. část

Načtení hodnot x a y z klávesnice
Jan Lánský
Úvod do programování 2. hodina
21

22. Euklidův algoritmus – II. část

Dokud menší z čísel y není nula
Počítáme zbytek po dělení většího čísla x menším y.
Původní menší číslo x se stane větším a zbytek po
dělení se stane menším číslem
Po první iteraci cyklu platí: x > y
Příklad: x = 6; y = 15;
zbytek = 6 % 15 // zbytek = 6
x = y // x = 15
y = zbytek // y = 6;
V průběhu
výpočtu se změní
x a y, musíme
vypsat nyní
Dokončíme výpis řádku s výsledkem
Jan Lánský
Úvod do programování 2. hodina
22

23. Cyklus for

Inicializace;
While(Podmínka) {
Příkaz;
Inkrement;
}
Cyklus for
for (inicializace;podmínka; inkrement)
příkaz;
1. krok – Inicializace
2. krok – Podmínka
i=0
i < 10
true – krok 3, false konec
3. krok – Příkaz
Console.Write(i)
i ++
4. krok – Inkrement
5. krok – Přejdeme na krok 2
Jan Lánský
Úvod do programování 2. hodina
23

24. Cyklus for

Hlavička cyklu
Syntax: for (inicializace;podmínka; inkrement) příkaz;
Tělo cyklu
Inicializace se provede pouze jednou na začátku cyklu
Podmínka (hodnota typu bool) se testuje na začátku každé
iterace cyklu. Je-li podmínka splněna iterace cyklu proběhne,
je-li podmínka nesplněna cyklus končí.
Inkrement se provádí na konci iterace cyklu
Iterace cyklu: test podmínky, (složený) příkaz, inkrement
Řídící proměnná cyklu – obvykle i, j, k, …
Incializace obvykle i=0
Podmínka obvykle i < hodnota
Inkrement obvykle i++
Jan Lánský
NEDĚLAT
Změna řídící
proměnné cyklu
v těle cyklu
Úvod do programování 2. hodina
24

25. Výpis čísel 0 až 9

Hlavička cyklu
Tělo cyklu - (složený)
příkaz
Řídící proměnná cyklu i začne na hodnotě 0.
Je-li i < 10 je splněna podmínka a vykoná se tělo cyklu
V každé iteraci cyklu se hodnota i vypíše.
Na konci každé iterace cyklu se hodnota i zvýší o 1
Po zvýšení hodnoty i na 10 bude podmínka nesplněna a
cyklus končí.
Jan Lánský
Úvod do programování 2. hodina
25

26. break a continue

break
Ukončí (nejvíce zanořený) cyklus
Pokračujeme zdrojovým kódem za cyklem
continue
Ukončí aktuální iteraci (nejvíce
zanořeného) cyklu.
Provede se inkrement (for cyklus)
Pokračuje se další iterací cyklu
Jan Lánský
Úvod do programování 2. hodina
26

27. Součet pěti čísel - break

Lidé číslují pořadí od 1, programátoři od 0
Zadané číslo nebylo kladné
Ukončení cyklu
Jan Lánský
Úvod do programování 2. hodina
27

28. Minimum z pěti čísel - continue

Minimum z pěti čísel continue
Kompilátor hlásí chybu (předposlední řádek),
pokud není min inicializované. Ale zbytečně.
Nekonečný
cyklus, pokud
budu zadávat
samá nekladná
čísla
Ukončení iterace cyklu
V první iteraci nové min vždy
Jan Lánský
Musel být while cyklus, ve for cyklu
by se provádělo i++ vždy
Úvod do programování 2. hodina
28

29. Dva vnořené cykly – pyramida

Přepisujeme max na jednom místě místo tří
Vnější cyklus
Vnitřní cyklus
Ořezání pravé strany
i <= max – j - 1
Ořezání levé strany
i <= j
Odřádkovat
Jan Lánský
Úvod do programování 2. hodina
29

30. Test prvočíselnosti

Prvočíslo má právě
dva dělitele 1 a
sebe sama. Proto 1
není prvočíslo
Číslo je prvočíslem dokud
neprokážeme opak
Číslo menší než 2 nejsou
prvočísla
Stačí zkoušet dělitele do odmocniny
Našli jsme dělitele není prvočíslo
Jan Lánský
Úvod do programování 2. hodina
30

31. Rozklad na prvočísla

Nalezen dělitel
Jednotlivé dělitele
oddělujeme *, ale ne prvního
dělitele
Write(i) nepotřebuji
formátovací řetězec
Musí být else, dělitele mohou
být násobné
Jan Lánský
Úvod do programování 2. hodina
31

32. Základy časové složitosti algoritmů

V současné době je čas běhu programu
důležitější než spotřebovaná paměť.
Časová složitost algoritmů se měří v
počtu operací nutných ke zpracování
vstupu dané délky n
Asymptotická složitost algoritmů
O(n), O(n log(n)), O(n2), O(n3). O(2n)
Jan Lánský
Úvod do programování 2. hodina
32

33. Časová složitost

Konstantní - O(1) zvýšení hodnoty čísla o jedna
Logaritmická - O(log n) najití prvku v setříděné
posloupnosti
Lineární - O(n) najití prvku v nesetříděné
posloupnosti
Lineárnělogaritmická - O(n log(n)) setřídění
posloupnosti chytře
Kvadratická - O(n2) setřídění posloupnosti hloupě
3
Kubická - O(n ) násobení matic (n řád matice)
Exponenciální - O(2n) obchodní cestující
Jan Lánský
Úvod do programování 2. hodina
33

34. Časová složitost a cykly

Cyklus procházející vstupní data O(n)
Dva vnořené cykly. V každém z cyklů
projdeme celá vstupní data O(n2)
Někdy cyklus proběhne výrazně
méněkrát než n vydělené konstantou
složitost algoritmu nutno matematicky
spočítat
Obvykle to bývá log(n)
Jan Lánský
Úvod do programování 2. hodina
34

35. Časová složitost - přijatelná

Rozdíl mezi O(n2) a O(n log(n))
n = 1 000 000 000 (roky vs sekundy)
Kvadratické algoritmy jsou problematické
pro velká data.
Rozdíl mezi O(n4) a O(2n)
n = 70 (milisekundy vs tisíce let)
Exponenciální algoritmy jsou použitelné jen
pro malá data
Jan Lánský
Úvod do programování 2. hodina
35

36. Zpětná vazba

Objevili jste ve slajdech chyby?
Včetně pravopisných
Nechápete nějaký slajd?
Je příliš obtížný, nesrozumitelný?
Máte nějaký nápad na vylepšení?
Anonymní formulář
Odeslání za pár vteřin
http://goo.gl/forms/WxkZqBsZLs
Jan Lánský
Úvod do programování 2. hodina
36