Похожие презентации:
Равенство, подобие треугольников
1. Равенство, подобие треугольников
§1Равенство треугольниковГеометрия,7 класс, с.57
1
2. Равенство, подобие треугольников
§1Равенство треугольниковПо двум сторонам и углу
между ними
По стороне и прилежащим
к ней углам
По трём сторонам
2
3.
Равенство равнобедренных треугольниковПо основанию и боковой
стороне
По основанию и прилежащему
(противолежащему) к нему углу
По боковой стороне и углу (при
основании или между боковыми
сторонами)
3
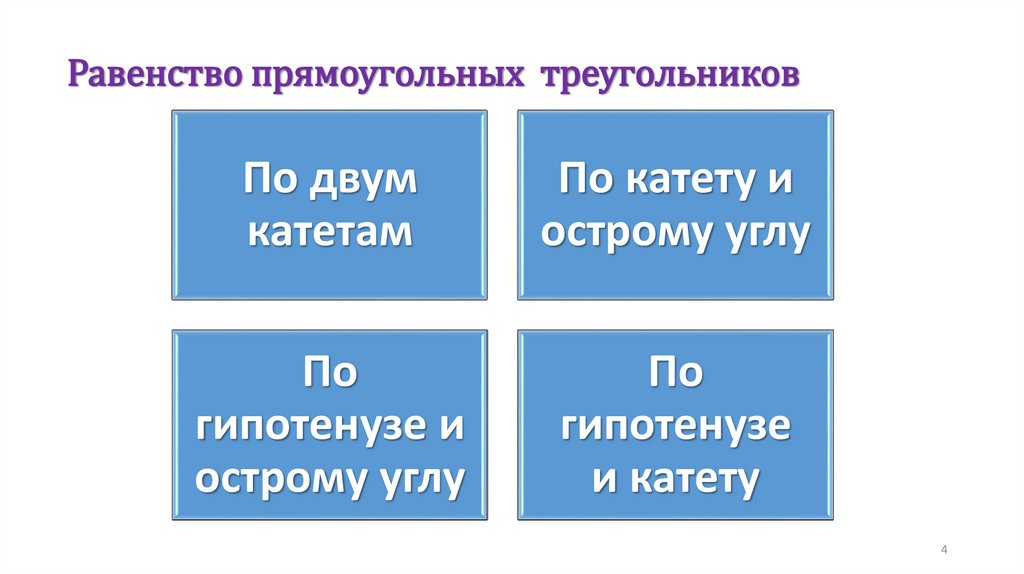
4.
Равенство прямоугольных треугольниковПо двум
катетам
По катету и
острому углу
По
гипотенузе и
острому углу
По
гипотенузе
и катету
4
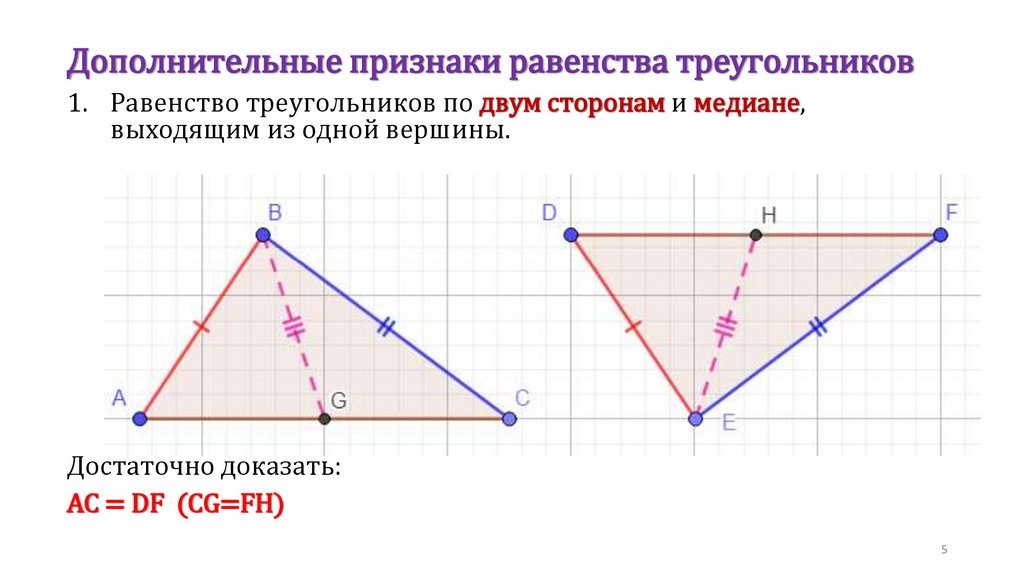
5.
Дополнительные признаки равенства треугольников1. Равенство треугольников по двум сторонам и медиане,
выходящим из одной вершины.
Достаточно доказать:
AC = DF (CG=FH)
5
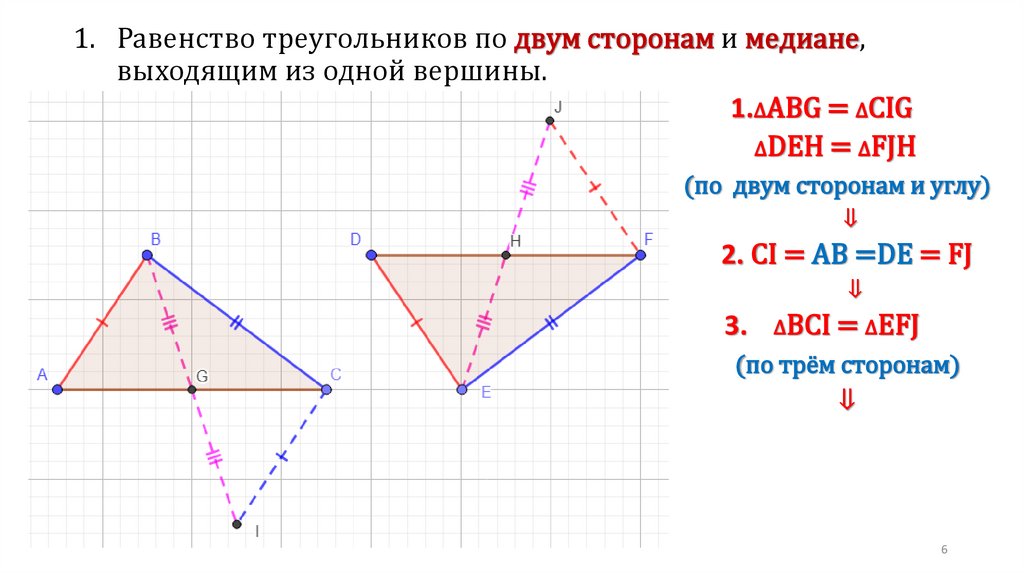
6.
1. Равенство треугольников по двум сторонам и медиане,выходящим из одной вершины.
1.∆ABG = ∆CIG
∆DEH = ∆FJH
(по двум сторонам и углу)
⇓
2. CI = AB =DE = FJ
⇓
3.
∆BCI = ∆EFJ
(по трём сторонам)
⇓
6
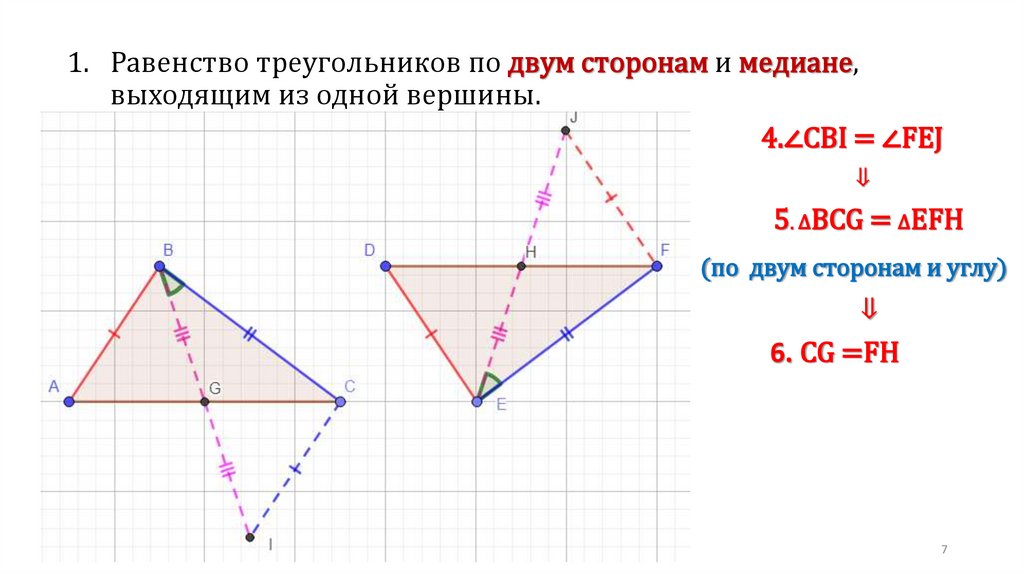
7.
1. Равенство треугольников по двум сторонам и медиане,выходящим из одной вершины.
4.∠CBI = ∠FEJ
⇓
5. ∆BCG = ∆EFH
(по двум сторонам и углу)
⇓
6. CG =FH
7
8.
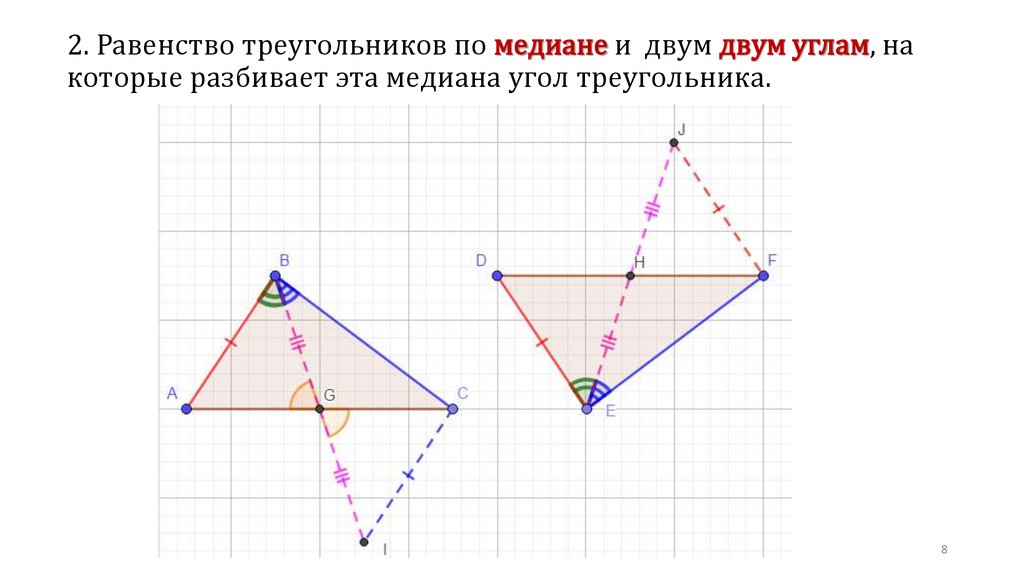
2. Равенство треугольников по медиане и двум двум углам, накоторые разбивает эта медиана угол треугольника.
8
9.
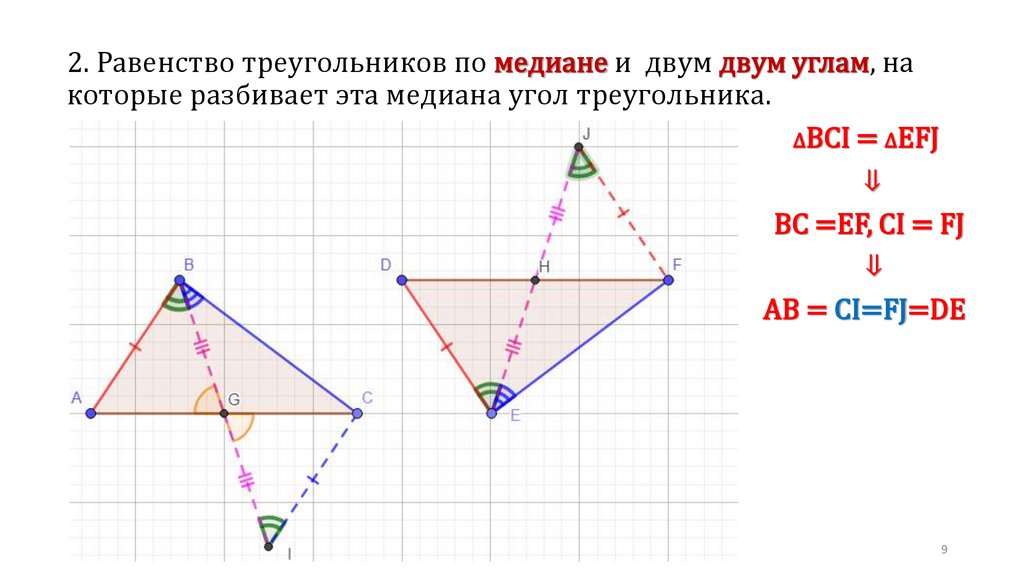
2. Равенство треугольников по медиане и двум двум углам, накоторые разбивает эта медиана угол треугольника.
∆BCI = ∆EFJ
⇓
BC =EF, CI = FJ
⇓
AB = CI=FJ=DE
9
10.
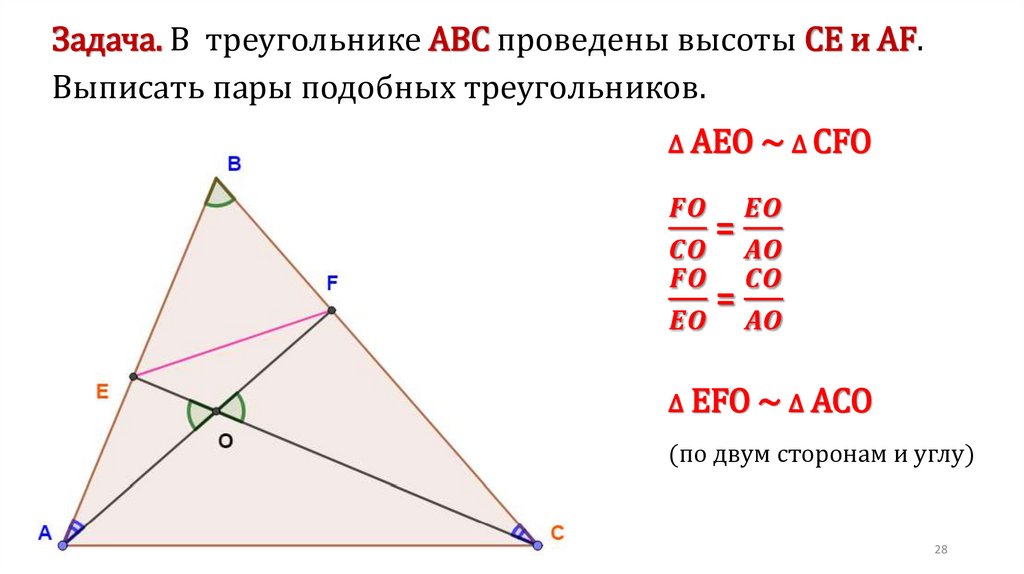
§2 Использование равенства треугольников прирешении задач
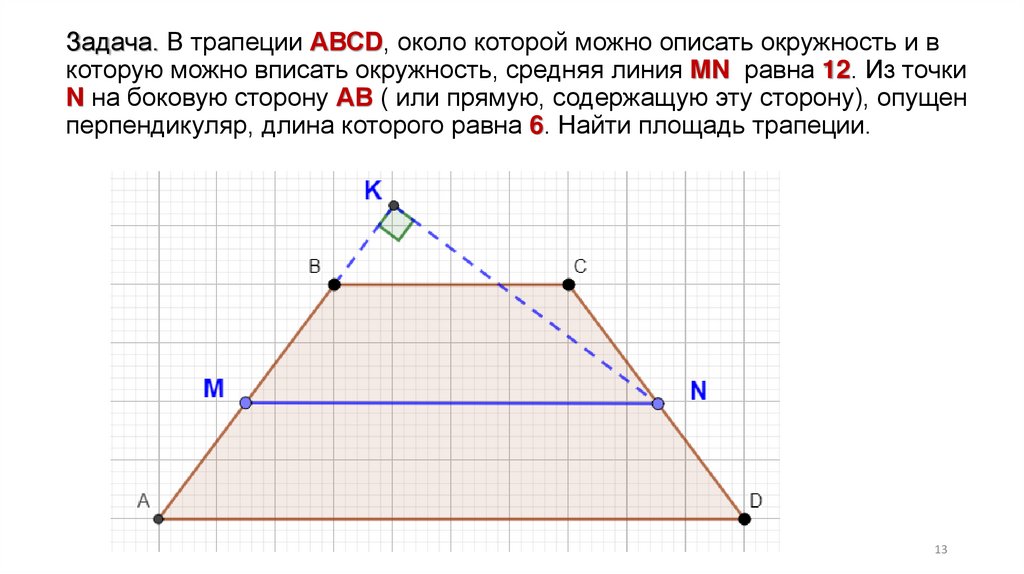
Задача. В трапеции АВСD, около которой можно
описать окружность и в которую можно вписать
окружность, средняя линия MN равна 12. Из точки N
на боковую сторону АВ ( или прямую, содержащую
эту сторону), опущен перпендикуляр, длина которого
равна 6. Найти площадь трапеции.
10
11.
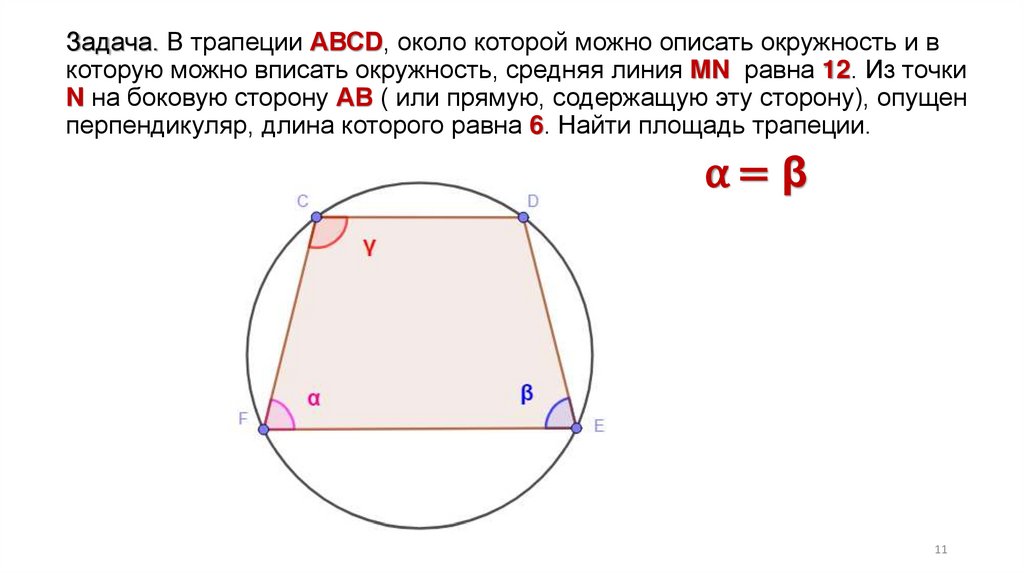
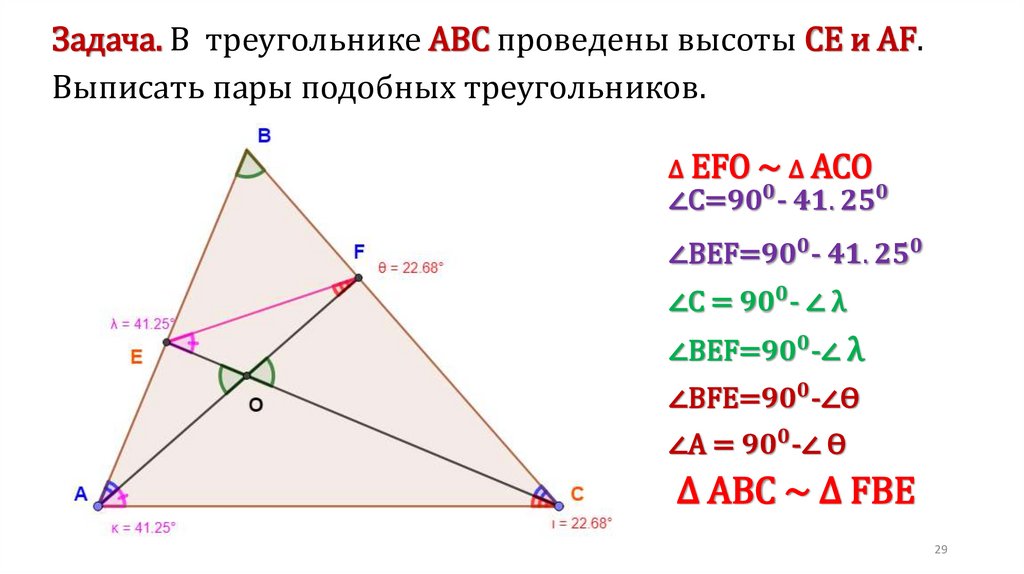
Задача. В трапеции АВСD, около которой можно описать окружность и вкоторую можно вписать окружность, средняя линия MN равна 12. Из точки
N на боковую сторону АВ ( или прямую, содержащую эту сторону), опущен
перпендикуляр, длина которого равна 6. Найти площадь трапеции.
α= β
11
12.
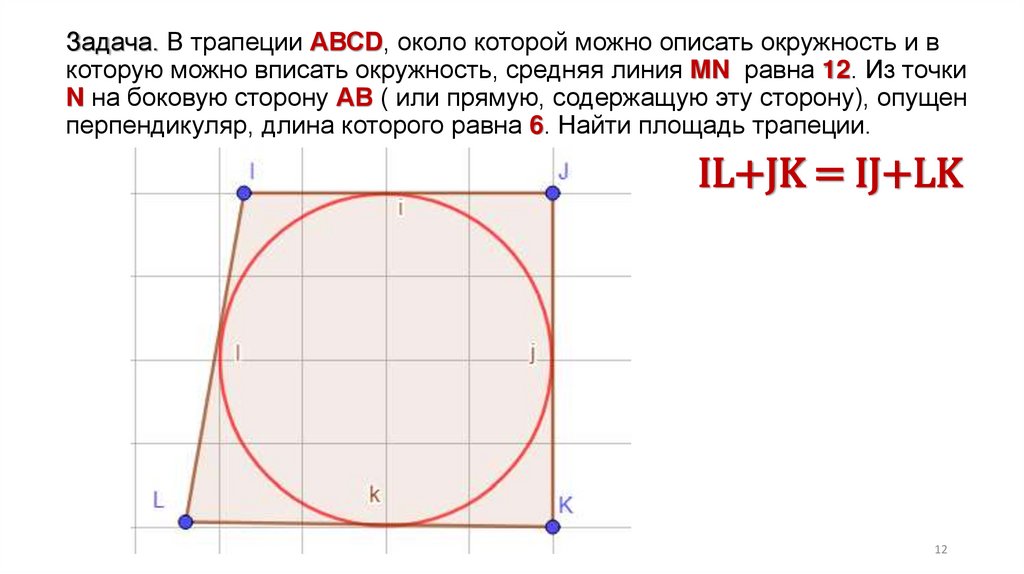
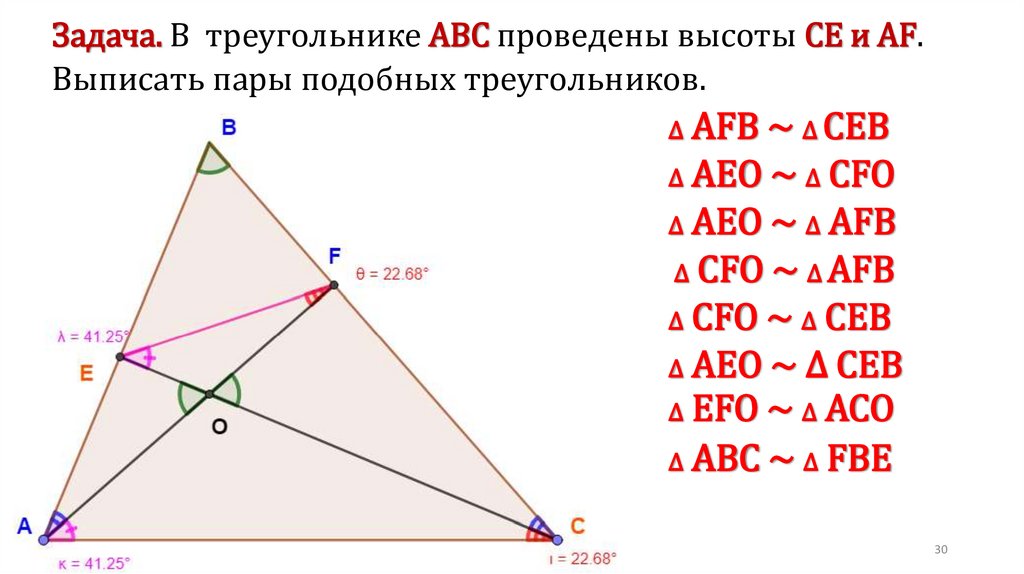
Задача. В трапеции АВСD, около которой можно описать окружность и вкоторую можно вписать окружность, средняя линия MN равна 12. Из точки
N на боковую сторону АВ ( или прямую, содержащую эту сторону), опущен
перпендикуляр, длина которого равна 6. Найти площадь трапеции.
IL+JK = IJ+LK
12
13.
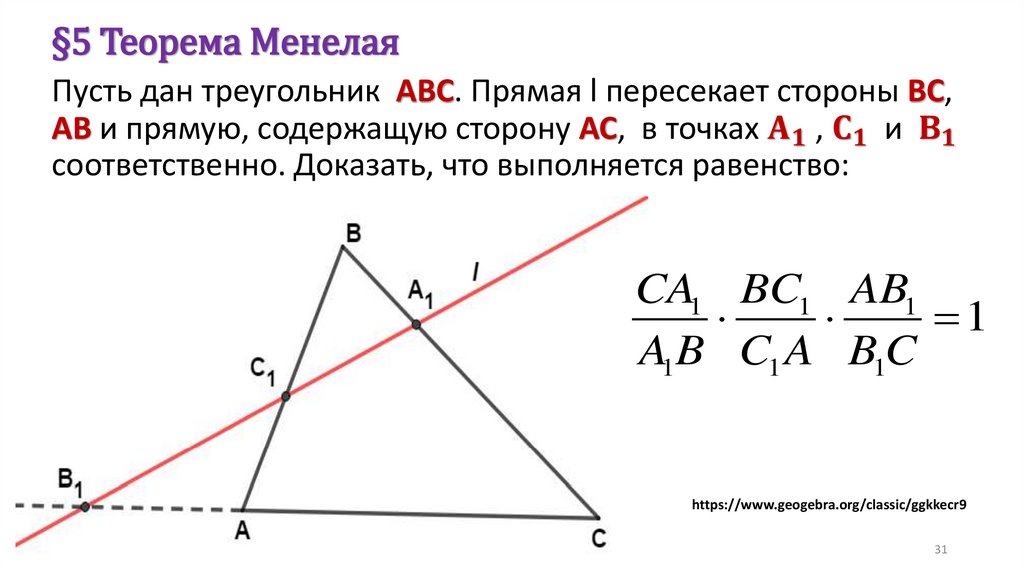
Задача. В трапеции АВСD, около которой можно описать окружность и вкоторую можно вписать окружность, средняя линия MN равна 12. Из точки
N на боковую сторону АВ ( или прямую, содержащую эту сторону), опущен
перпендикуляр, длина которого равна 6. Найти площадь трапеции.
13
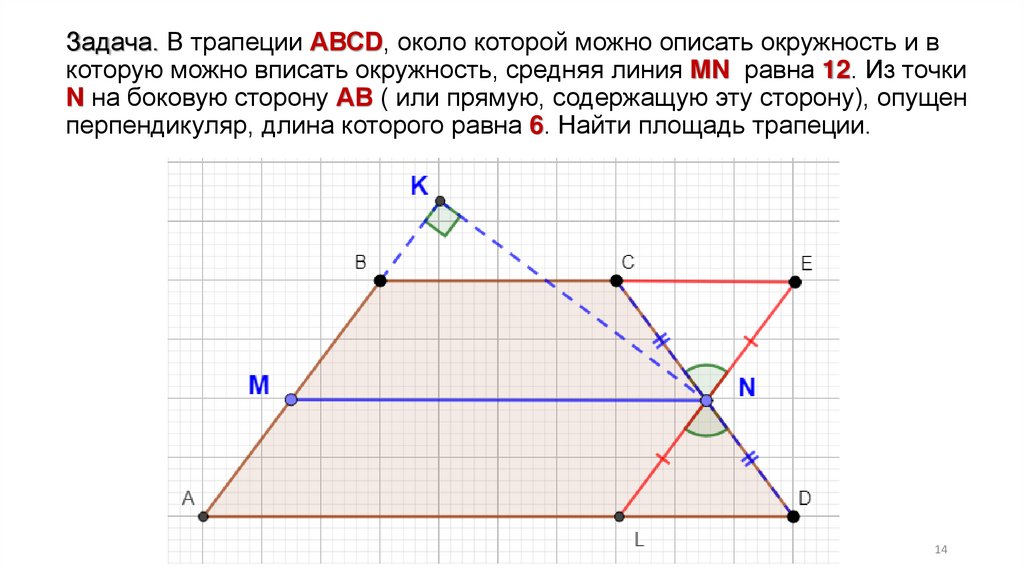
14.
Задача. В трапеции АВСD, около которой можно описать окружность и вкоторую можно вписать окружность, средняя линия MN равна 12. Из точки
N на боковую сторону АВ ( или прямую, содержащую эту сторону), опущен
перпендикуляр, длина которого равна 6. Найти площадь трапеции.
14
15.
1516.
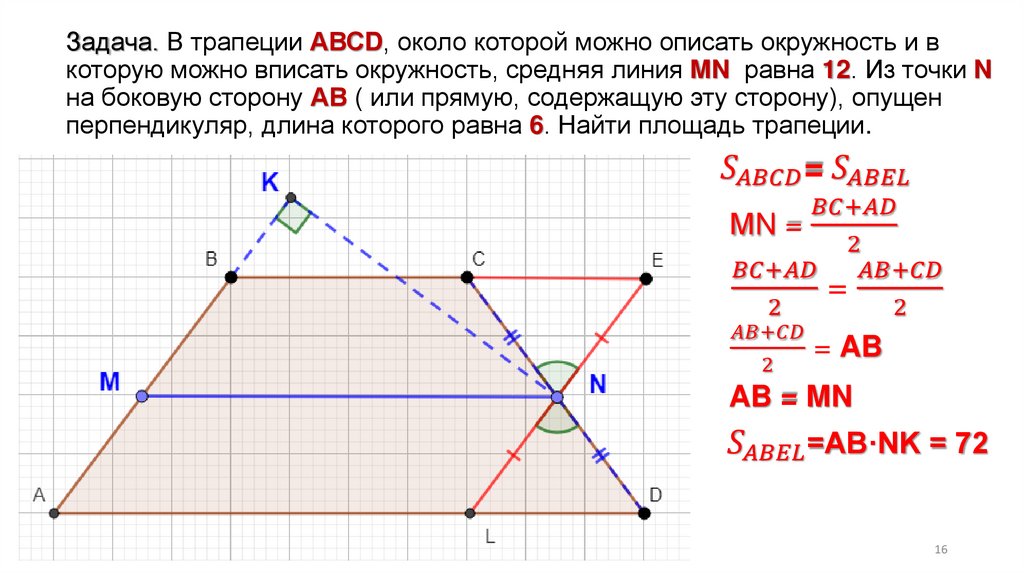
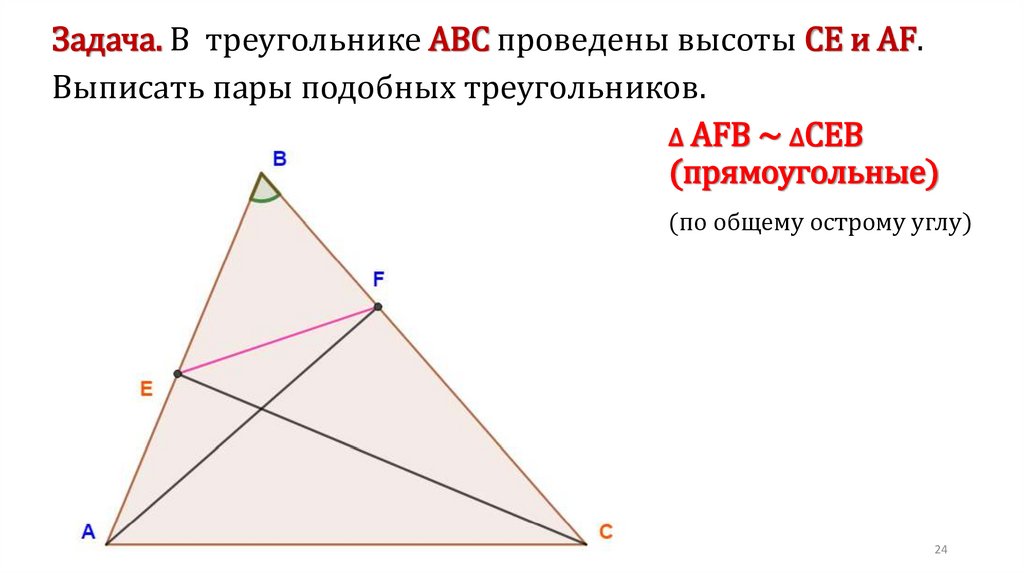
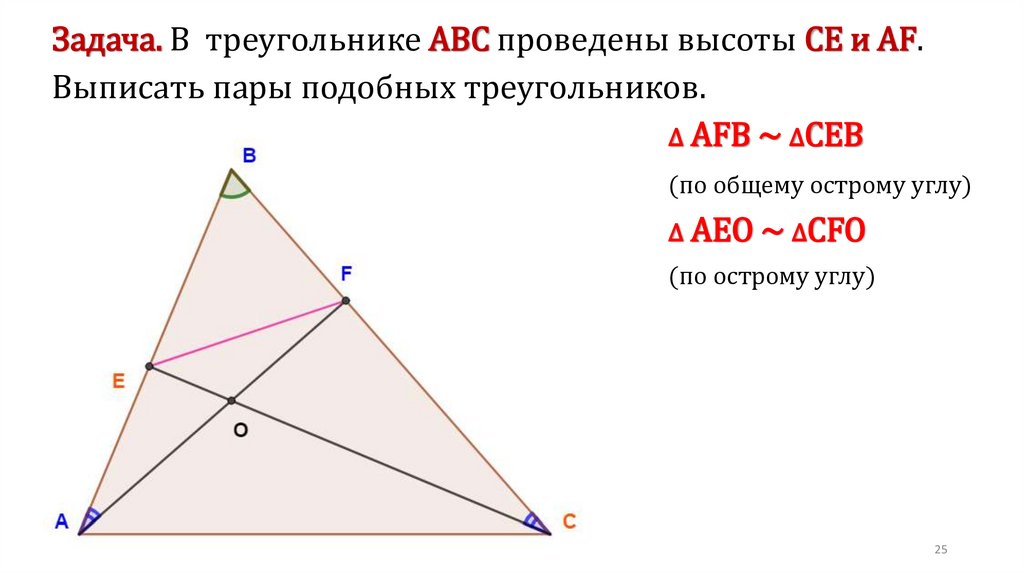
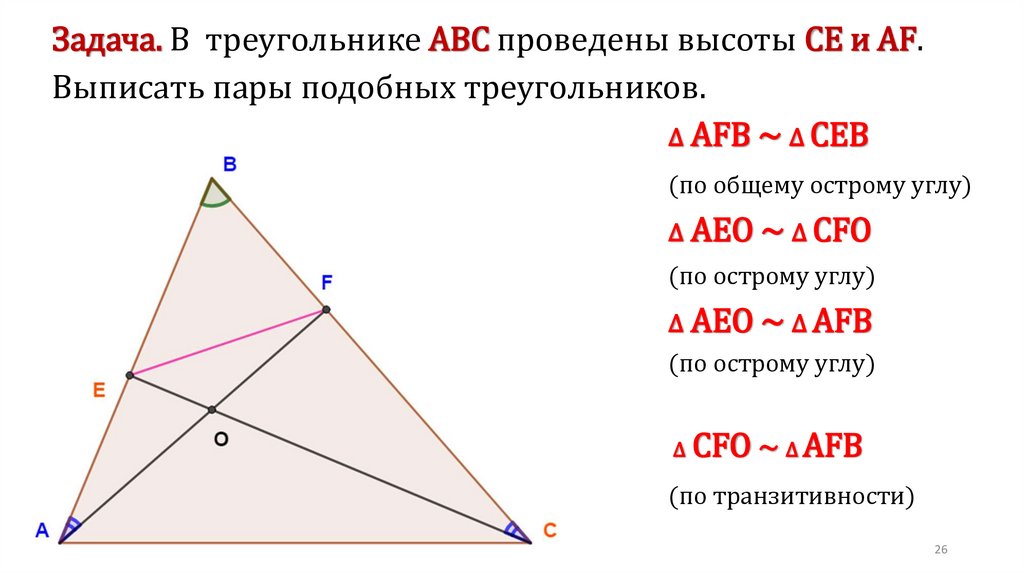
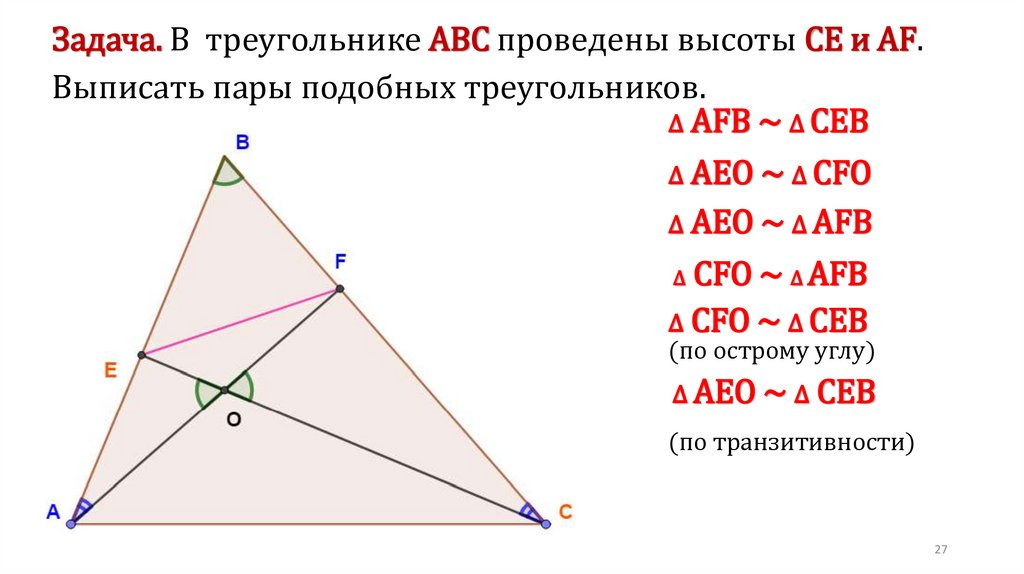
Задача. В трапеции АВСD, около которой можно описать окружность и вкоторую можно вписать окружность, средняя линия MN равна 12. Из точки N
на боковую сторону АВ ( или прямую, содержащую эту сторону), опущен
перпендикуляр, длина которого равна 6. Найти площадь трапеции.









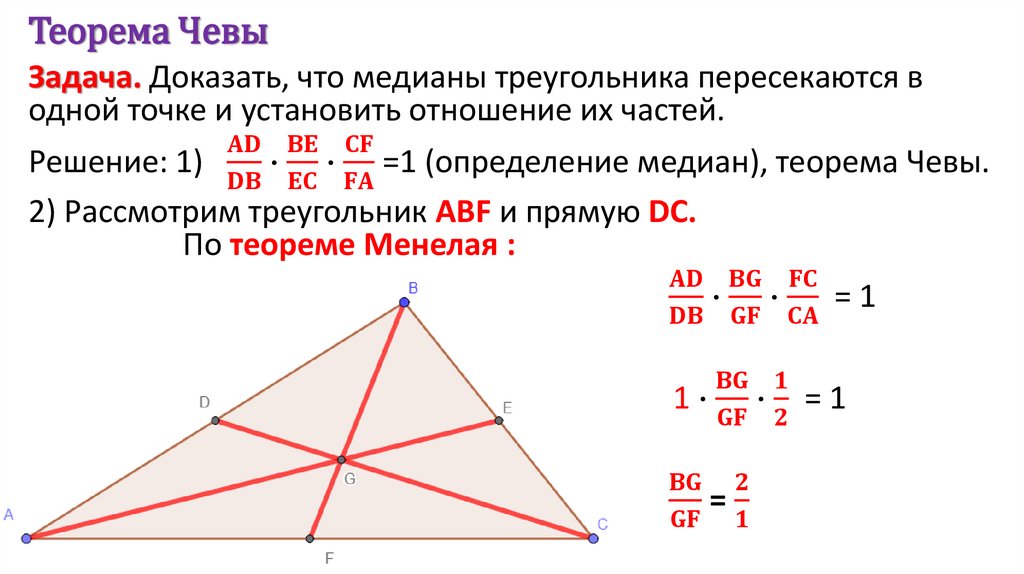
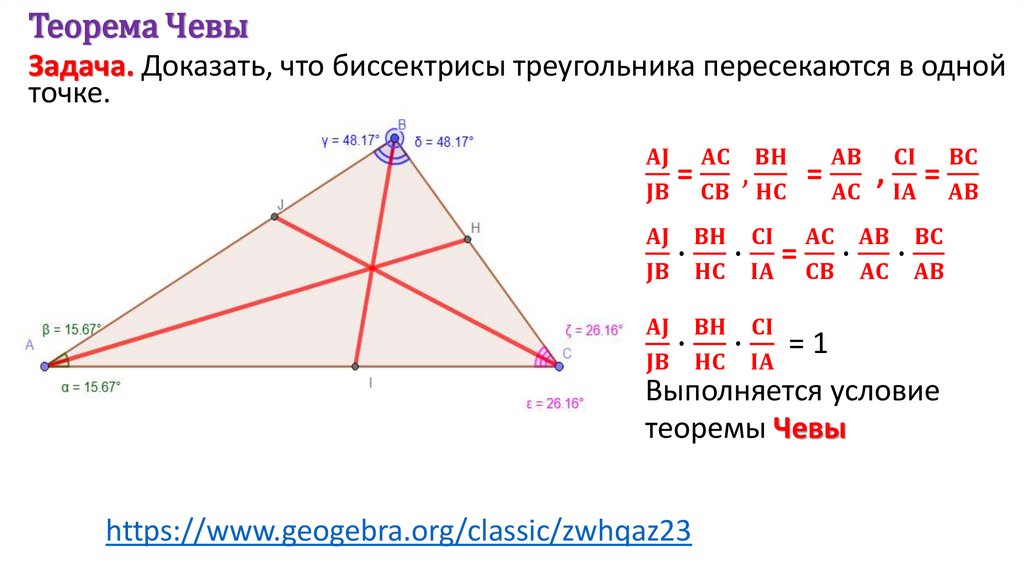
 Математика
Математика








