705c21ae748f434fa5b413d62b349c02

1. Алгебра 9 класс «Уравнения приводимые к квадратным. Биквадратные уравнения»

2. Девиз урока:

«Ум человеческий только тогда
понимает обобщения, когда он
сам его сделал или проверил»
Л.Н. Толстой

3. Актуализация знаний учащихся:

1) Какое уравнение называется квадратным?
2) Что называется дискриминантом
квадратного уравнения?
3) Какие виды квадратных уравнений вы
знаете?
4) Какое квадратное уравнение называется
неполным?

4.

5) Какое уравнение называется
приведенным? Какой формулой оно задается?
6) По каким формулам находятся корни
квадратных уравнений?
7) Сформулируйте теорему Виета.
8) Сформулируйте обратную теорему Виета.

5. Устный счет.

6. Кроссворд.

1. Третья степень числа.
2. Подкоренное выражение в формуле
корней квадратного уравнения?
3. Значение переменной, обращающее
уравнение в верное равенство.
4. Уравнение, имеющие одинаковые корни.
5. Равенство с переменной.

7.

6. Квадратное уравнение, с первым
коэффициентом равным нулю.
7. Многочлен в правой части квадратного
уравнения.
8. равенство, содержащие число и
переменные.
9. Французский математик.
10. Числовой множитель в произведении.
11. Множество корней уравнения.

8.

9. Цели урока:

Дать определение биквадратного
уравнения, научиться решать
биквадратные уравнения,
исследовать корни биквадратного
уравнения.

10. Определение.

11. Алгоритм решения биквадратного уравнения:

1) Введем в уравнение новую переменную
путем обозначения какого- то выражения
из этого уравнения;
2) Вместо этого выражения подставляем
новую переменную и получим квадратное
уравнение относительно новой
переменной;

12.

3) Решаем полученное квадратное уравнение;
4) Способом подстановки находим значение
исходной переменной;
5) С помощью проверки определяем корни
данного уравнения.

13. Пример:

14.

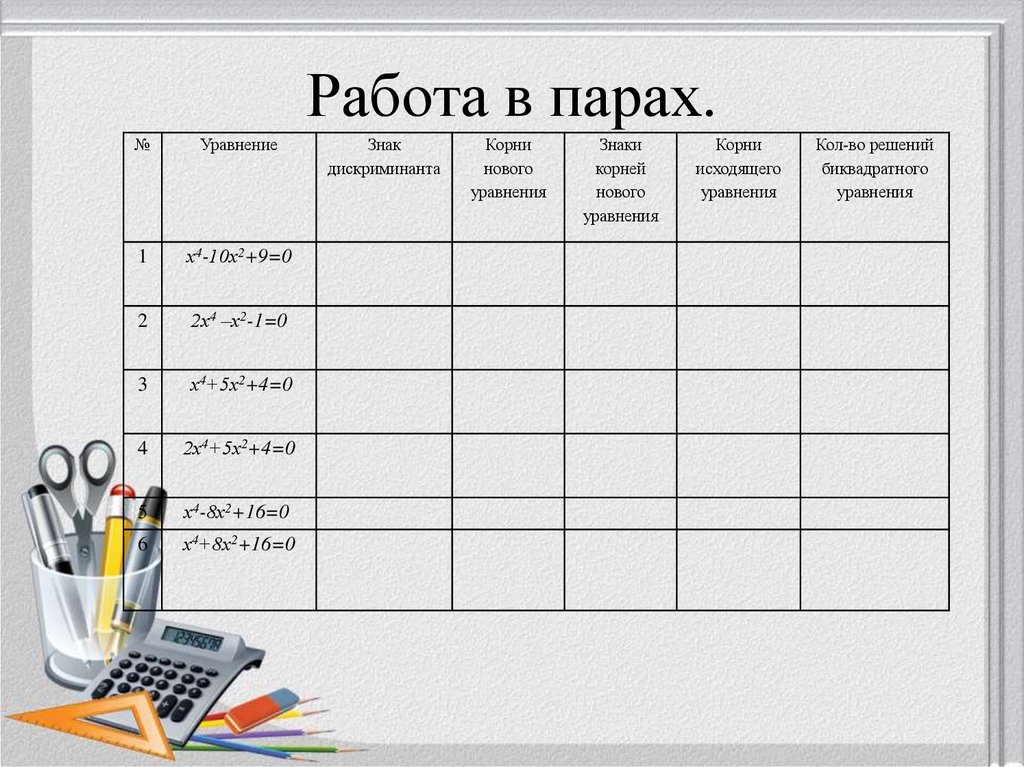
15. Работа в парах.

№
Уравнение
1
х4-10х2+9=0
2
2х4 –х2-1=0
3
х4+5х2+4=0
4
2х4+5х2+4=0
5
х4-8х2+16=0
6
х4+8х2+16=0
Знак
дискриминанта
Корни
нового
уравнения
Знаки
корней
нового
уравнения
Корни
исходящего
уравнения
Кол-во решений
биквадратного
уравнения

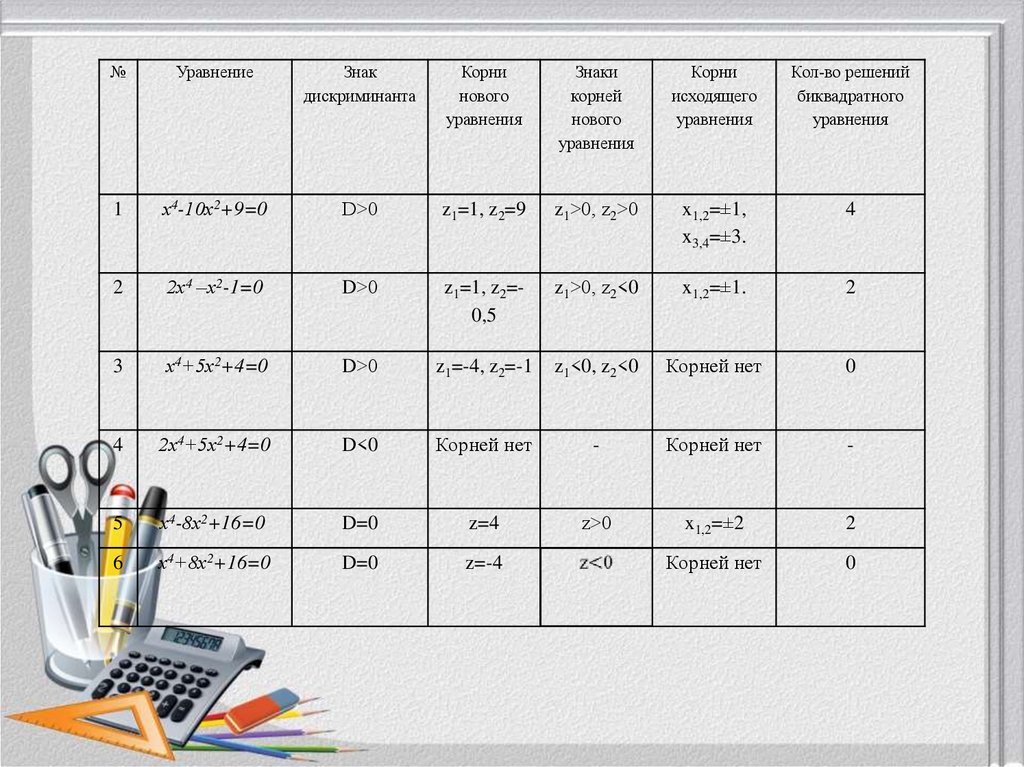
16.

№
Уравнение
Знак
дискриминанта
Корни
нового
уравнения
Знаки
корней
нового
уравнения
Корни
исходящего
уравнения
Кол-во решений
биквадратного
уравнения
1
х4-10х2+9=0
D˃0
z1=1, z2=9
z1˃0, z2˃0
x1,2=±1,
x3,4=±3.
4
2
2х4 –х2-1=0
D˃0
z1=1, z2=0,5
z1˃0, z2<0
x1,2=±1.
2
3
х4+5х2+4=0
D˃0
z1=-4, z2=-1
z1<0, z2<0
Корней нет
0
4
2х4+5х2+4=0
D<0
Корней нет
-
Корней нет
-
5
х4-8х2+16=0
D=0
z=4
z˃0
x1,2=±2
2
6
х4+8х2+16=0
D=0
z=-4
Корней нет
0

17. Работа с учебником.

Выполняем у доски и на месте

18. Задание на дом.

19. Итог урока.

1. Какие же уравнения называются
биквадратными?
2. Алгоритм решения биквадратного
уравнения?
3. От чего зависит число решений
биквадратного уравнения?

20.

Спасибо за урок!