Похожие презентации:
Циліндр, його елементи. Переріз площинами
1.
2. Циліндр, його елементи. Переріз площинами
ЦИЛІНДР, ЙОГОЕЛЕМЕНТИ.
ПЕРЕРІЗ
ПЛОЩИНАМИ
3.
4.
План:Тіла обертання
Означення циліндра
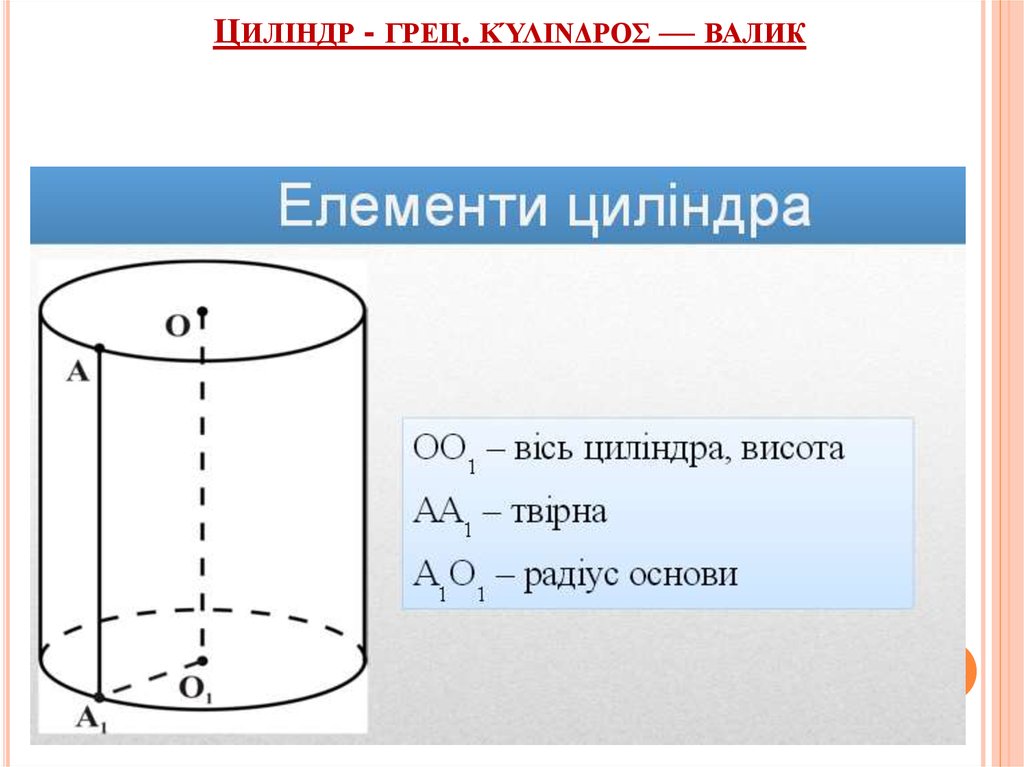
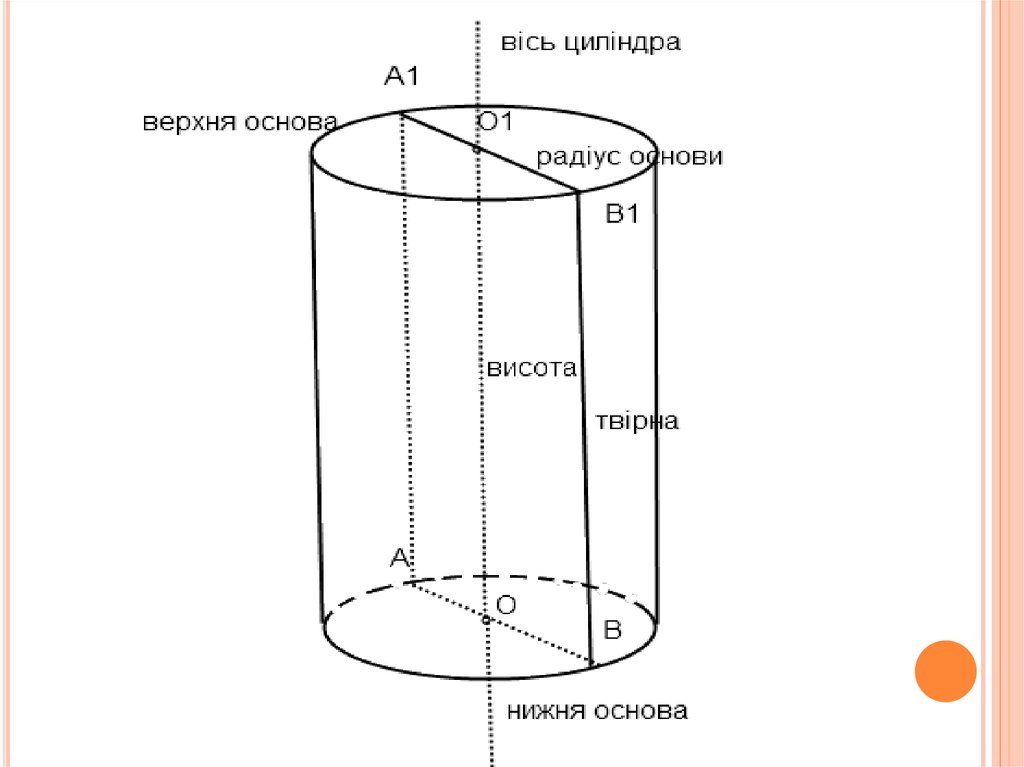
Елементи циліндра
Перерізи циліндра
Площа поверхні циліндра
Розв’язування задач
5.
Ніколи ще до нашого часу ми не жили в такийгеометричний період…
Навколишній світ – це світ геометрії, чистий,
істинний, бездоганний у наших очах. Все навколо
- геометрія.
Ле Корбюзьє
6.
Тіла та поверхні обертанняУявимо, що плоский многокутник АВСВ обертається
навколо прямої АВ (рис. 1, а). При цьому кожна його точка, що не
належить прямій АВ, описує коло з центром на цій прямій.
Весь многокутник АВСВ, обертаючись навколо прямої АВ,
описує деяке тіло обертання (рис. 1, б). Поверхня цього тіла
називається поверхнею обертання. Пряму АВ називають віссю
обертання цього тіла.
Будь-яка площина, що проходить через вісь тіла обертання, перетинає це тіло.
Утворений переріз називають осьовим перерізом тіла
обертання.
7.
8. Циліндр - грец. κύλινδρος — валик
ЦИЛІНДР - ГРЕЦ. ΚΎΛΙΝΔΡΟΣ — ВАЛИК9.
10.
11.
Осьовий переріз циліндра — прямокутник зісторонами, що дорівнюють висоті циліндра і
діаметру його основи.
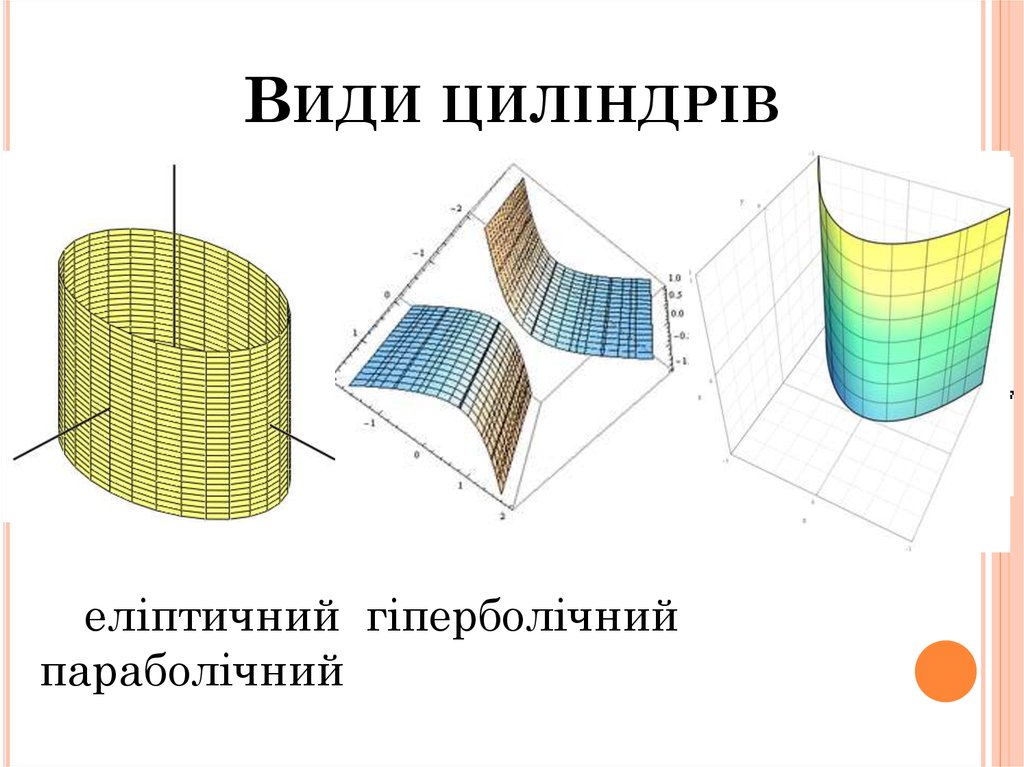
12. Види циліндрів
ВИДИ ЦИЛІНДРІВеліптичний гіперболічний
параболічний
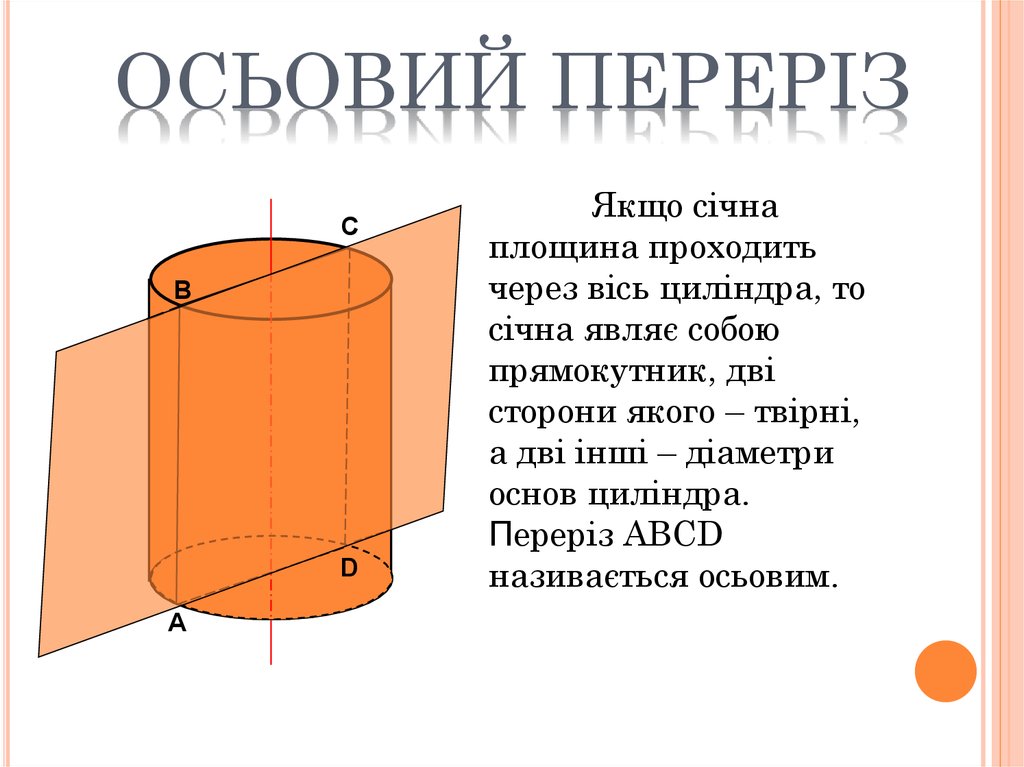
13. Осьовий переріз
ОСЬОВИЙ ПЕРЕРІЗC
B
D
A
Якщо січна
площина проходить
через вісь циліндра, то
січна являє собою
прямокутник, дві
сторони якого – твірні,
а дві інші – діаметри
основ циліндра.
Переріз ABCD
називається осьовим.
14. Теорема 1: Переріз циліндра площиною, паралельною його осі, є прямокутник.
ТЕОРЕМА 1: ПЕРЕРІЗ ЦИЛІНДРА ПЛОЩИНОЮ,ПАРАЛЕЛЬНОЮ ЙОГО ОСІ, Є ПРЯМОКУТНИК.
Доведення:
Дійсно,
січна
площина
перетинає бічну поверхню
циліндра по твірних АВ і СD,
які рівні і паралельні, крім
того, АВ АD, СD АD. Отже,
чотирикутник
АВСD
—
прямокутник.
15. Круговий переріз
КРУГОВИЙ ПЕРЕРІЗС
γ
О
α
Круговий
переріз – це переріз
циліндра площиною,
паралельною його
основам.Площина,
паралельна площині
основи циліндра,
перетинає його бічну
поверхню по колу,
яку дорівнює колу
основи.
16. Теорема 2: Переріз циліндра площиною, паралельною основам циліндра, є круг, який дорівнює основі
ТЕОРЕМА 2: ПЕРЕРІЗ ЦИЛІНДРА ПЛОЩИНОЮ,ПАРАЛЕЛЬНОЮ ОСНОВАМ ЦИЛІНДРА, Є КРУГ,
ЯКИЙ ДОРІВНЮЄ ОСНОВІ
Доведення:
Дійсно,
січна
площина
перетинає циліндр по кругу,
бо, якщо виконати паралельне
перенесення
уздовж
осі
циліндра, яке суміщає січну
площину з площиною основи
циліндра,
то
переріз
суміститься з кругом.
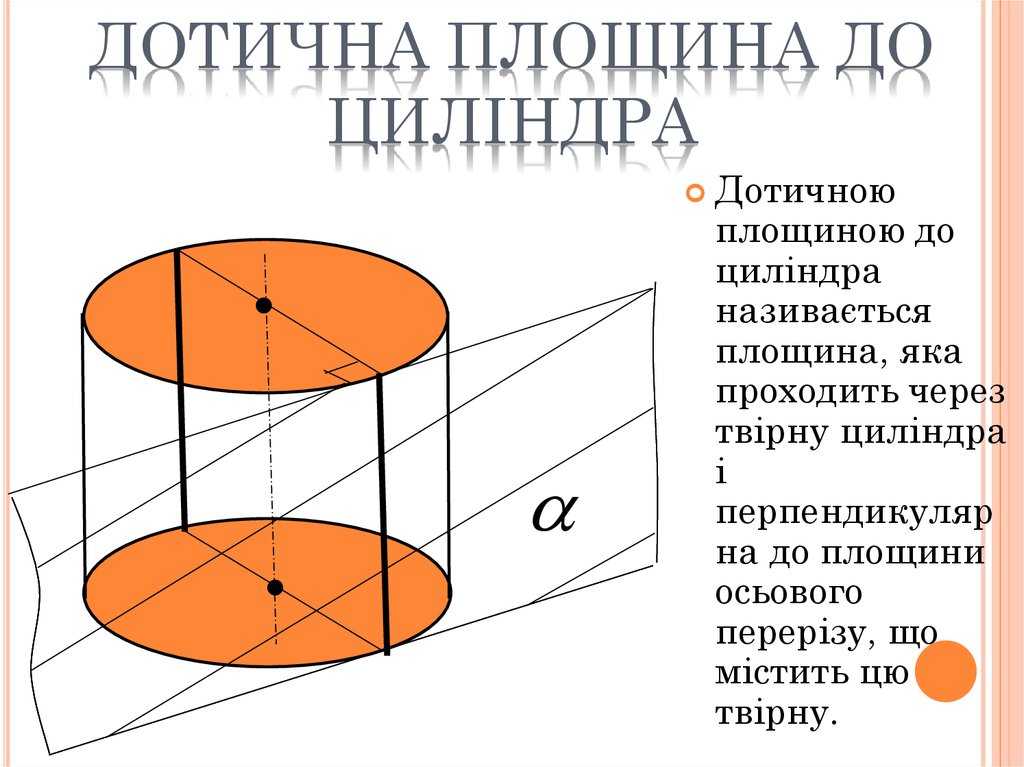
17. Переріз циліндра площиною, паралельною його осі
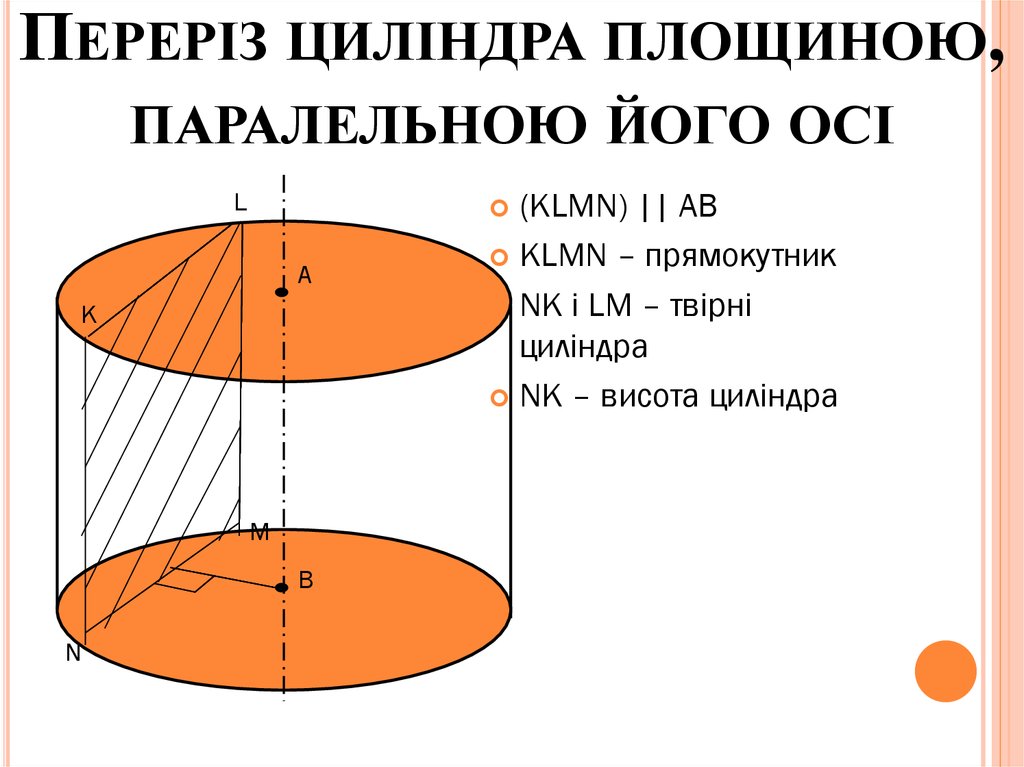
ПЕРЕРІЗ ЦИЛІНДРА ПЛОЩИНОЮ,ПАРАЛЕЛЬНОЮ ЙОГО ОСІ
L
A
K
M
B
N
(KLMN) || AB
KLMN – прямокутник
NK і LM – твірні
циліндра
NK – висота циліндра
18. Прямий Круговий циліндр
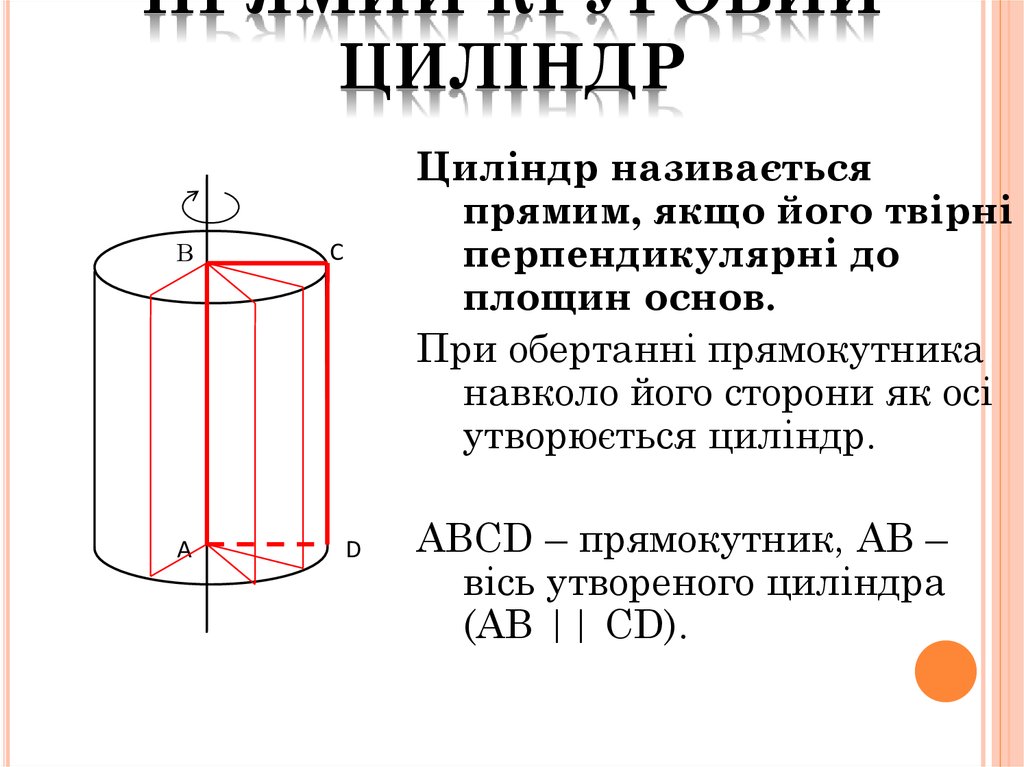
ПРЯМИЙ КРУГОВИЙЦИЛІНДР
В
А
Циліндр називається
прямим, якщо його твірні
перпендикулярні до
площин основ.
При обертанні прямокутника
навколо його сторони як осі
утворюється циліндр.
C
D
ABCD – прямокутник, АВ –
вісь утвореного циліндра
(AB || CD).
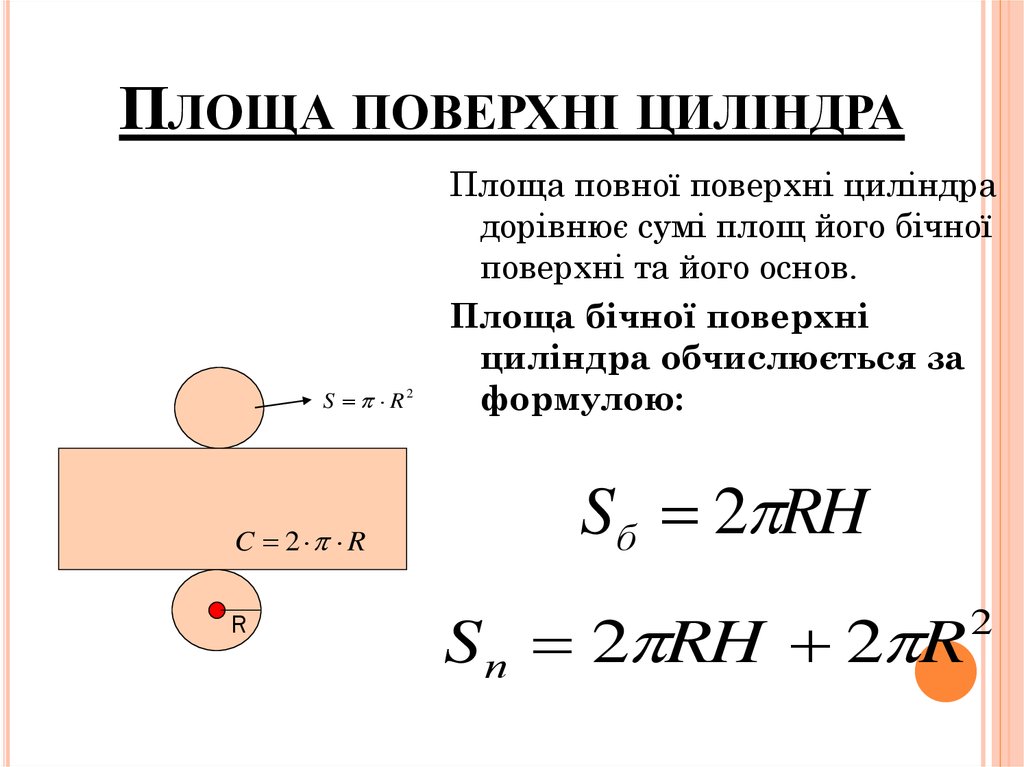
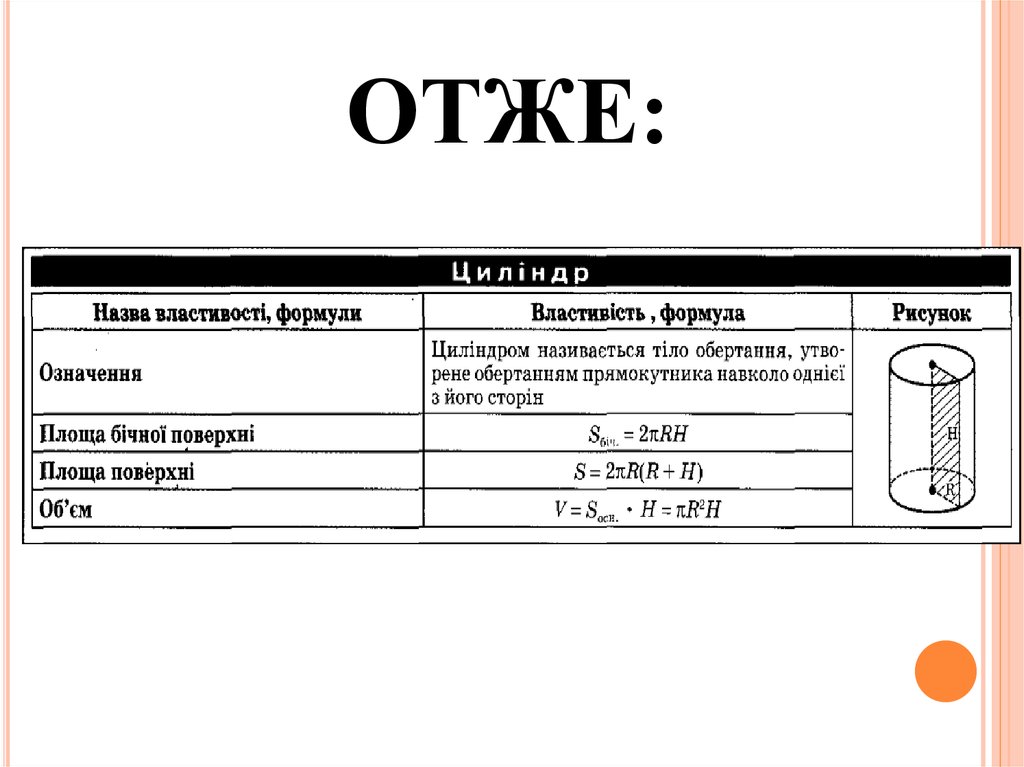
19. Площа поверхні циліндра
ПЛОЩА ПОВЕРХНІ ЦИЛІНДРАS R2
C 2 R
R
Площа повної поверхні циліндра
дорівнює сумі площ його бічної
поверхні та його основ.
Площа бічної поверхні
циліндра обчислюється за
формулою:
Sб 2 RH
S п 2 RH 2 R
2
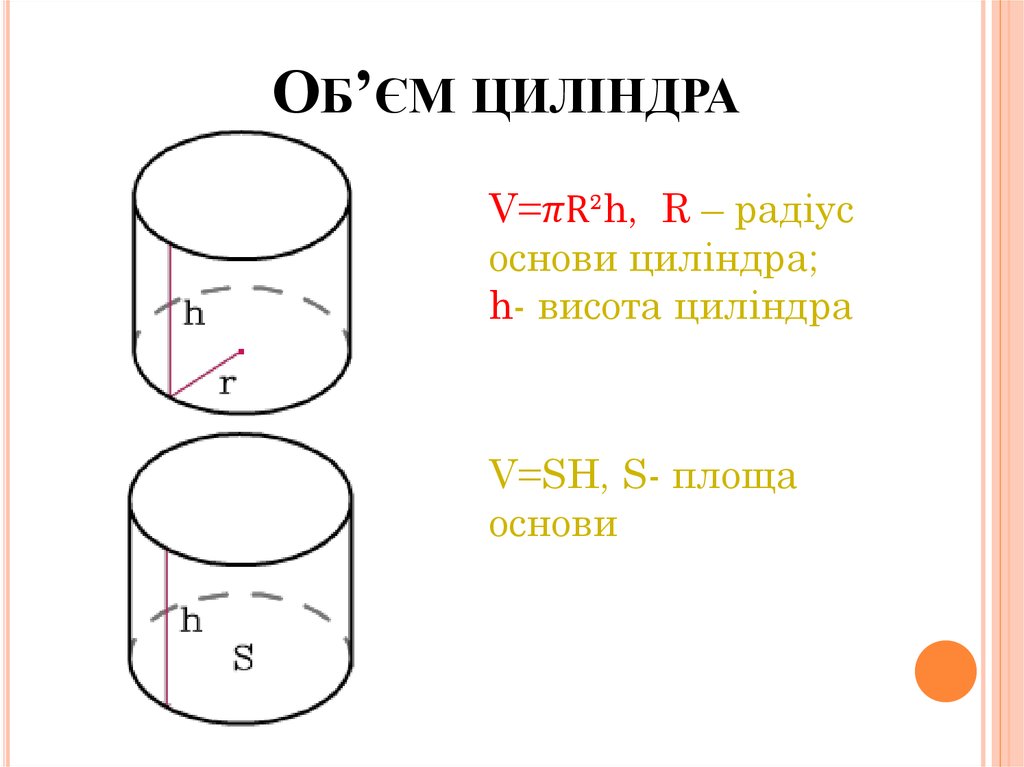
20. Об’єм циліндра
ОБ’ЄМ ЦИЛІНДРАV=



























 Математика
Математика








