Тема 1.4. для студентов (1)

1. Кодирование числовой информации в компьютере

Подготовлена преподавателем
информатики: Хасановой И.С.

2. ОБЪЯВЛЕНИЕ!

Записать в кратце лекцию.
2. Выполнить задания из 10 слайда, 15 слайда и
22 слайда.
3. Выполнить Домашнюю работу.
4. Отправить мне на проверку.
1.

3. Двоичный код

Вся информация, которую обрабатывает
компьютер, должна быть представлена
двоичным кодом с помощью двух цифр – 0 и 1.
Эти два символа 0 и 1 принято называть битами
(от англ. binary digit – двоичный знак).

4. Кодирование и декодирование

Кодирование – преобразование входной
информации в форму, воспринимаемую
компьютером, т.е. двоичный код.
Декодирование – преобразование данных из
двоичного кода в форму, понятную человеку.

5. Способы кодирования

Способы кодирования и декодирования
информации в компьютере, в первую очередь,
зависит от вида информации, а именно, что
должно кодироваться: числа, текст,
графические изображения или звук.

6. Представление чисел

Для записи информации о количестве объектов
используются числа. Числа записываются с
использование особых знаковых систем,
которые называют системами счисления.
Система счисления – совокупность приемов и
правил записи чисел с помощью определенного
набора символов.

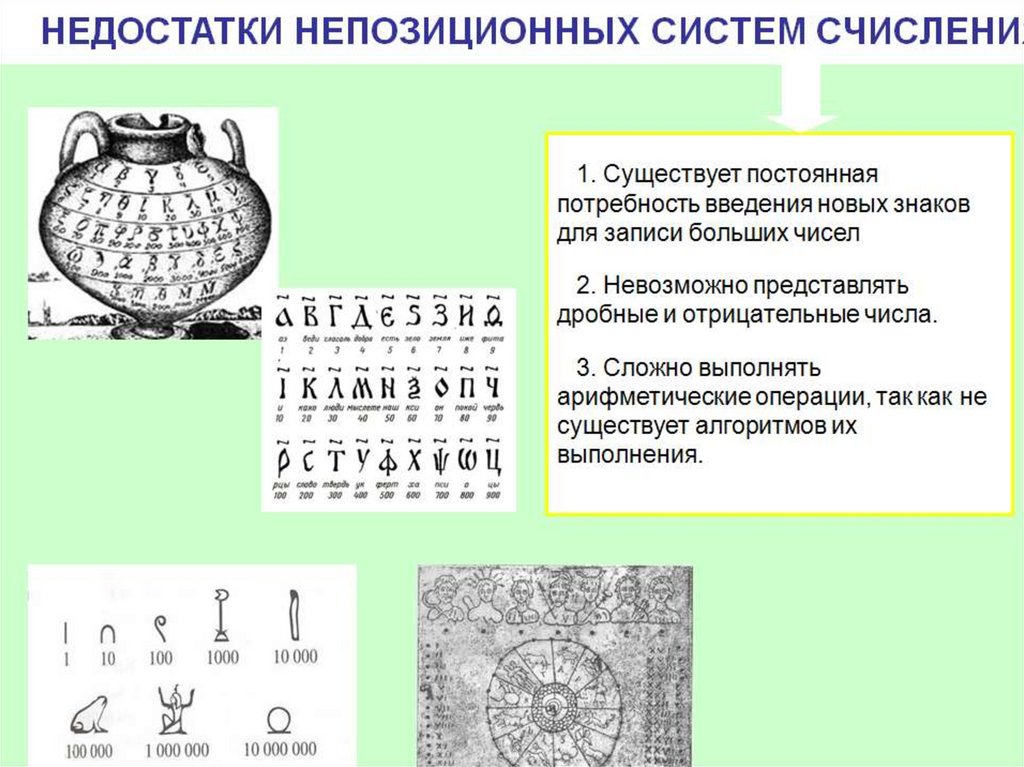
7. Позиционные и непозиционные системы счисления

Все системы счисления делятся на две большие
группы:
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
Количественное значение каждой
цифры числа зависит от того, в
каком месте (позиции или
разряде) записана та или иная
цифра.
Количественное значение цифры
числа не зависит от того, в каком
месте (позиции или разряде)
записана та или иная цифра.
0,7
7
70
XIX

8.

9. Римская непозиционная система счисления

Самой распространенной из непозиционных
систем счисления является римская. В качестве
цифр используются: I(1), V(5), X(10), L(50), C(100),
D(500), M(1000).
Величина числа определяется как сумма или
разность цифр в числе.
MCMXCVIII = 1000+(1000-100)+(10010)+5+1+1+1 = 1998

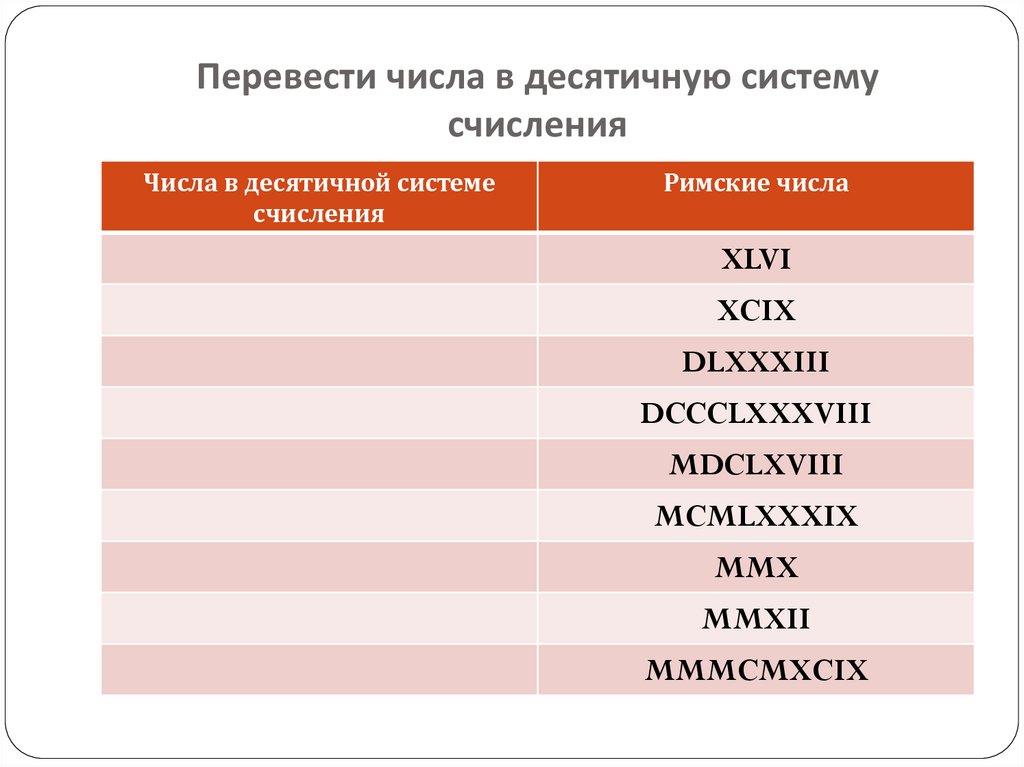
10. Перевести числа в десятичную систему счисления

Числа в десятичной системе
счисления
Римские числа
XLVI
XCIX
DLXXXIII
DCCCLXXXVIII
MDCLXVIII
MCMLXXXIX
MMX
MMXII
MMMCMXCIX

11.

12. Позиционные системы счисления

Первая позиционная система счисления была
придумана еще в Древнем Вавилоне, причем
вавилонская
нумерация
была
шестидесятеричная,
т.е.
в
ней
использовалось шестьдесят цифр!
В
XIX
веке
довольно
широкое
распространение
получила
двенадцатеричная система счисления.
В настоящее время наиболее распространены
десятичная, двоичная, восьмеричная и
шестнадцатеричная системы счисления.

13.

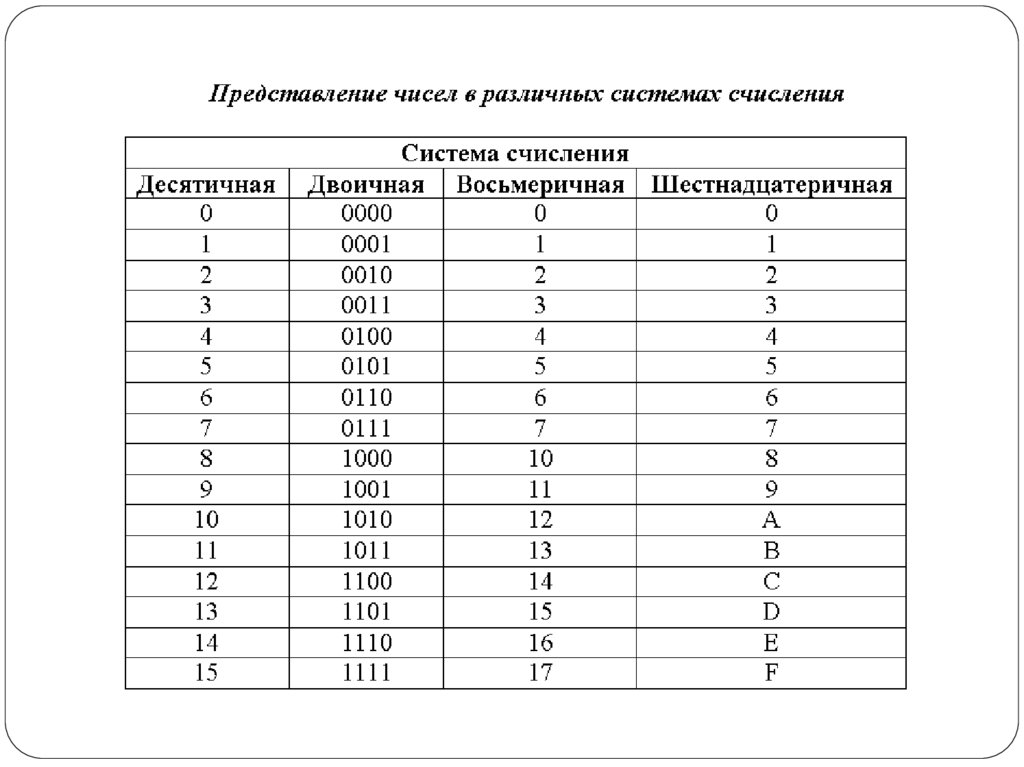
14. Основание системы счисления

Количество различных символов, используемых
для изображения числа в позиционных
системах счисления, называется основанием
системы счисления.
Система счисления
Основание
Алфавит цифр
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

15. 13810 = 100010102

Перевод из десятичной системы
Счисления в двоичную
13810 = 100010102
самостоятельное задание
11110 =
7910 =

16. Перевод из двоичной системы счисления в десятичную

20=1
21=2
22=4
23-8
24-16
25=32
26=64
27=128
28=256
3 2 10
6354 – тысяч (разряд 4, 103 ) - 6
сотен (разряд 3, 102) – 3
десяток (разряд 2, 101) – 5
единиц (разряд 1, 100) – 4
6354= 6*103+3*102+5*101+4*100
7 65432 10
10101001= 1*27+0*26+1*25+0*24+1*23+0*22+0*21+1*20 =
128+32+8+1=169

17.

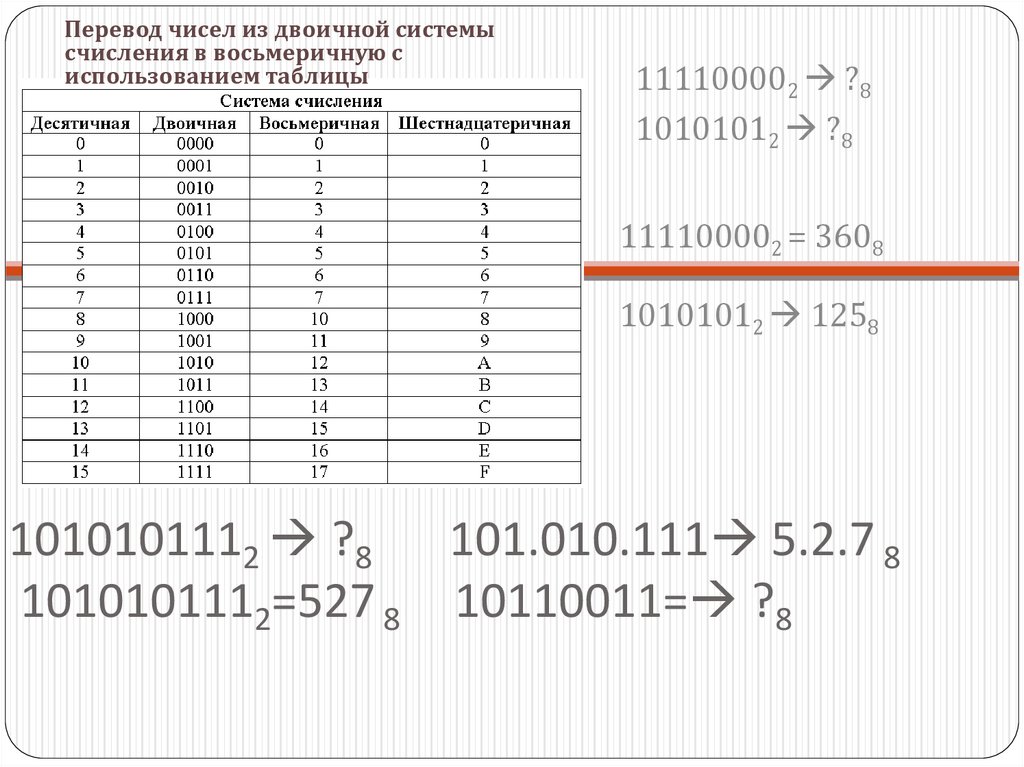
18. 1010101112  ?8 101.010.111 5.2.7 8 1010101112=527 8 10110011= ?8

Перевод чисел из двоичной системы
счисления в восьмеричную с
использованием таблицы
111100002 ?8
10101012 ?8
111100002 = 3608
10101012 1258
1010101112 ?8 101.010.111 5.2.7 8
1010101112=527 8 10110011= ?8

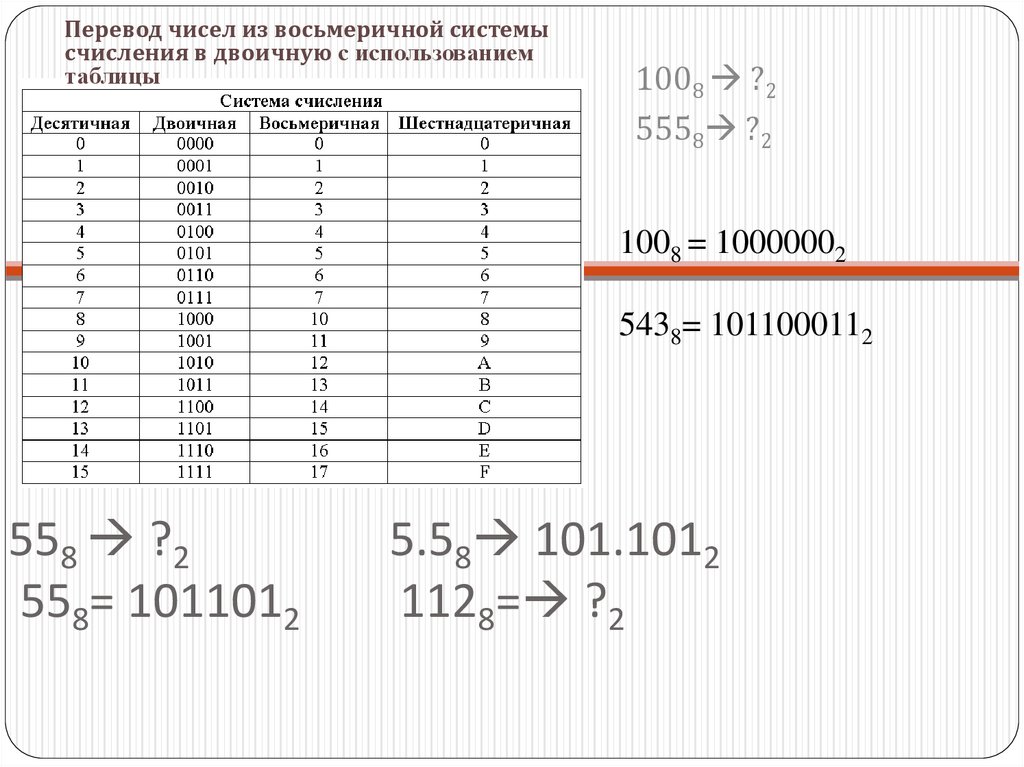
19. 558  ?2 5.58 101.1012 558= 1011012 1128= ?2

Перевод чисел из восьмеричной системы
счисления в двоичную с использованием
таблицы
1008 ?2
5558 ?2
1008 = 10000002
5438= 1011000112
558 ?2
558= 1011012
5.58 101.1012
1128= ?2

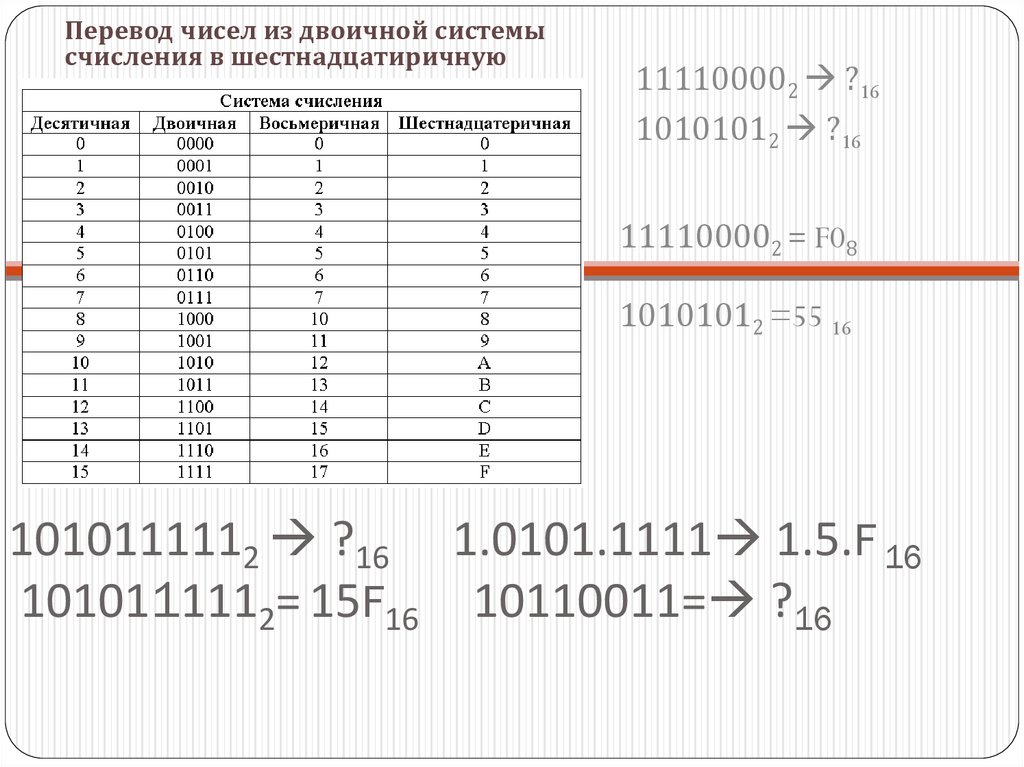
20. 1010111112  ?16 1.0101.1111 1.5.F 16 1010111112= 15F16 10110011= ?16

Перевод чисел из двоичной системы
счисления в шестнадцатиричную
111100002 ?16
10101012 ?16
111100002 = F08
10101012 =55 16
1010111112 ?16 1.0101.1111 1.5.F 16
1010111112= 15F16 10110011= ?16

21. Расположите числа, записанные в различных системах счисления, в порядке возрастания

1 вариант
3510, 368, 3А16, 1001012
2 вариант
1110012, 648, 9Е16, 2510

22. 5B16  ?2 5.B8 0101.10112 5B8= 1011011 2 1c28= ?2

Перевод чисел из шестнадцатеричной
системы счисления в двоичную с
использованием таблицы
1016 ?2
55516 ?2
1016 = 100002
5FC16= 101111111002
5B16 ?2
5B8= 1011011 2
5.B8 0101.10112
1c28= ?2

23. Домашнее задание:

1. Перевести в римскую систему
счисления:
2985
3485
2. Перевести из десятичной системы
счисления в двоичную числа: 39; 101;
256
3. Перевести из двоичной системы
счисления в десятичную : 10101;
111000; 1000000;
(