Практика 1

1. Расчеты, сбережения, кредиты

Практика 3.

2. Задача 1.

• Вкладчик имеет возможность положить в банк на депозит 500
тыс. руб. на 3 года. Выбор производится между двумя банками.
Определите, какой вариант наиболее выгоден для вкладчика,
если банки предлагают следующие схемы. Первый банк — 7,5 %
годовых с начислением и выплатой процентов по истечении
каждого года; второй банк — 7 % с ежемесячным начислением
процентов и их капитализацией, а также выплатой их вместе со
всей суммой по истечении срока вклада.

3.

• Банк 1:
• Сумма вклада (P): 500 000 руб.
• Срок (n): 3 года.
• Ставка (i₁): 7,5% годовых = 0,075.
• Условия: Проценты начисляются и выплачиваются в конце каждого года.
Это означает, что проценты не присоединяются к основной сумме (нет
капитализации), а выводятся на отдельный счет или карту вкладчика.
• Банк 2:
• Сумма вклада (P): 500 000 руб.
• Срок (n): 3 года.
• Номинальная ставка (i₂): 7% годовых = 0,07.
• Условия: Ежемесячное начисление процентов с капитализацией. Это
означает, что проценты присоединяются к телу вклада каждый месяц, и в
следующем периоде начисление идет на увеличенную сумму. Выплата
всей суммы (вклад + проценты) происходит в конце срока.

4. Расчет дохода по первому банку

• Здесь все просто, так как проценты не капитализируются, а
выплачиваются.
• Годовой доход = Сумма вклада × Годовая ставка
• Годовой доход = 500 000 × 0,075 = 37 500 руб.
• Такой доход вкладчик будет получать каждый год в течение 3 лет.
• Общий доход за 3 года (I₁) = Годовой доход × Количество лет
• I₁ = 37 500 × 3 = 112 500 руб.
• Итоговая сумма на руках (S₁): Так как проценты выплачивались
ежегодно, на счете в банке к концу срока останется только
первоначальная сумма вклада. Но общая сумма денег у вкладчика
будет:
• S₁ = Вклад + Все полученные проценты = 500 000 + 112 500 = 612 500 руб.

5. Расчет дохода по второму банку

Здесь используется формула сложных процентов с ежемесячной
капитализацией:
S = P × (1 + i / m)^{n × m}
Где:
•S – итоговая сумма, которую получит вкладчик в конце срока.
•P – первоначальная сумма вклада (500 000 руб.).
•i – номинальная годовая ставка (0,07).
•n – срок вклада в годах (3 года).
•m – количество периодов начисления процентов в году (12, так как
капитализация ежемесячная).

6.

Подставляем значения в формулу:
S₂ = 500 000 × (1 + 0,07 / 12)^{3 × 12}
Производим вычисления по шагам:
1.0,07 / 12 ≈ 0,0058333 (это месячная процентная ставка).
2.1 + 0,0058333 = 1,0058333.
3.3 × 12 = 36 (столько раз произойдет начисление процентов за
весь срок).
4.Возводим в степень: (1,0058333)³⁶. Расчет этого значения:
•Можно использовать калькулятор с функцией x^y.
•(1,0058333)³⁶ ≈ 1,2332.
5.S₂ = 500 000 × 1,2332 = 616 600 руб.
Теперь находим доход (I₂), который получит вкладчик:
•I₂ = S₂ - P = 616 600 - 500 000 = 116 600 руб.

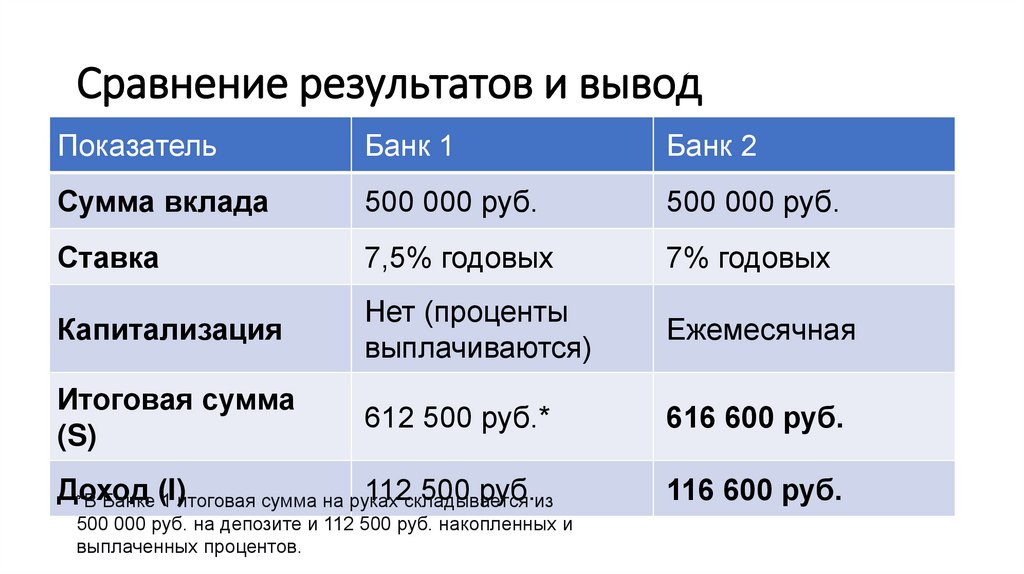
7. Сравнение результатов и вывод

Показатель
Банк 1
Банк 2
Сумма вклада
500 000 руб.
500 000 руб.
Ставка
7,5% годовых
7% годовых
Капитализация
Нет (проценты
выплачиваются)
Ежемесячная
Итоговая сумма
(S)
612 500 руб.*
616 600 руб.
Доход
112складывается
500 руб.из
*В Банке (I)
1 итоговая сумма на руках
116 600 руб.
500 000 руб. на депозите и 112 500 руб. накопленных и
выплаченных процентов.

8. Вывод:

• Несмотря на то, что годовая ставка во втором банке (7%) ниже,
чем в первом (7,5%), за счет эффекта ежемесячной
капитализации процентов итоговый доход оказывается выше.
• Наиболее выгодным для вкладчика является второй банк, так
как он принесет на 4 100 руб. больше дохода за три года.
• Ключевой урок: При выборе вклада нельзя ориентироваться
только на размер процентной ставки. Необходимо учитывать
наличие и частоту капитализации, так как она может сделать
вклад с более низкой номинальной ставкой более доходным.