математика

1.

“Колледж менеджмента”
Логарифмы в науке
Выполнила
студентка
группы 25 О/П:
Ковязина А.Д

2.

Что такое логарифмы в науке?
Логарифм в науке – это
показатель степени, в
которую нужно возвести
число-основание,
чтобы
получить другое число.
1

3.

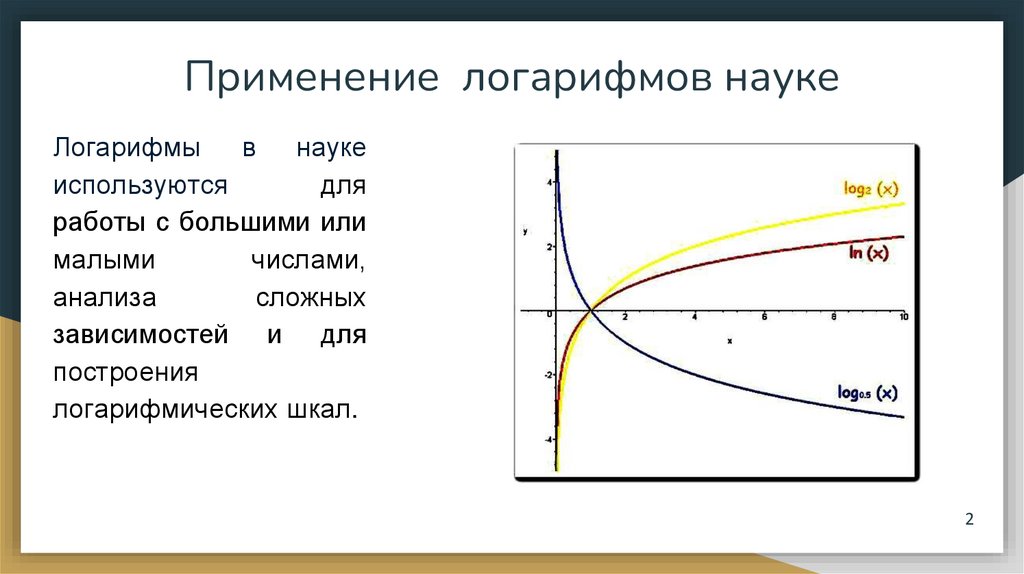
Применение логарифмов науке
Логарифмы в науке
используются
для
работы с большими или
малыми
числами,
анализа
сложных
зависимостей и для
построения
логарифмических шкал.
2

4.

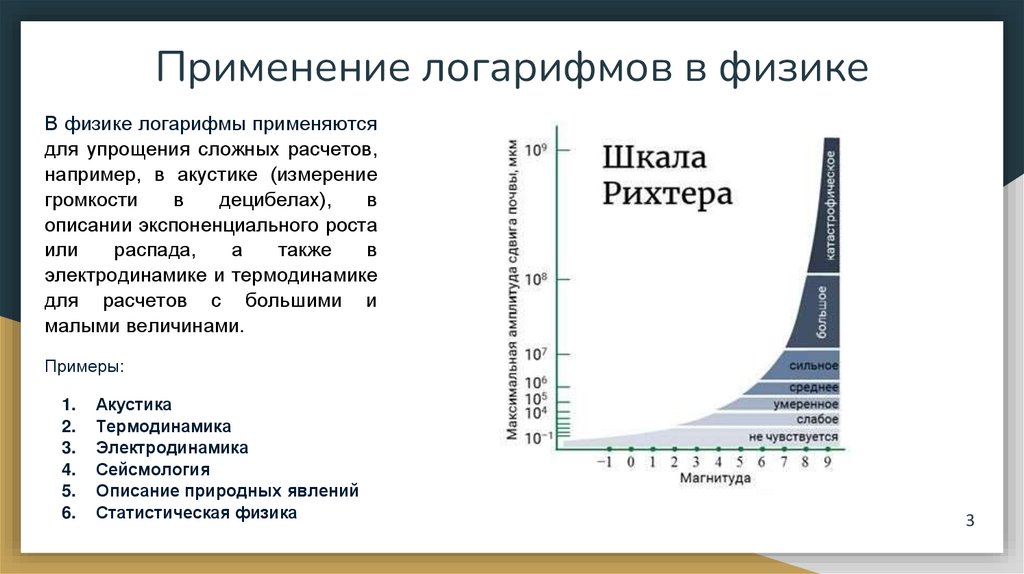
Применение логарифмов в физике
В физике логарифмы применяются
для упрощения сложных расчетов,
например, в акустике (измерение
громкости
в
децибелах),
в
описании экспоненциального роста
или
распада,
а
также
в
электродинамике и термодинамике
для расчетов с большими и
малыми величинами.
Примеры:
1.
2.
3.
4.
5.
6.
Акустика
Термодинамика
Электродинамика
Сейсмология
Описание природных явлений
Статистическая физика
3

5.

Применение логарифмов в астрономии
В астрономии логарифмы применяются
для работы с гигантскими диапазонами
величин, в частности, для измерения
звездных величин, которые являются
логарифмической
шкалой
яркости
небесных объектов, и для упрощения
вычислений расстояний и масштабов в
космосе.
Измерение яркости звезд (Звездные
величины)
1.
2.
Логарифмическая шкала
Диапазон яркости
Масштабы в астрономии
Гигантские расстояния
Логарифмические спирали
4

6.

Применение логарифмов в биологии
В биологии логарифмы применяются для
описания
и
моделирования
процессов
экспоненциального
роста
(например,
размножение микроорганизмов), а также для
анализа
явлений,
где
наблюдается
логарифмическая спираль, например, в форме
раковин моллюсков или паутины пауков.
Например:
Рост популяций
Логарифмическая спираль
Логарифмические шкалы
5

7.

Применение логарифмов в экономике
В экономике логарифмы применяют
для анализа сложных процентов,
оценки темпов роста, а также для
преобразования мультипликативных
зависимостей в аддитивные, что
упрощает экономические модели.
Пример:
Оценка темпов роста
Анализ
факторов
экономическом
моделировании:
в
6

8.

Вывод: Логарифм используется в науке для работы с большими диапазонами значений
и преобразования сложных экспоненциальных процессов в более простые, что
позволяет описывать такие явления, как радиоактивный распад, рост популяций,
акустические и сейсмические шкалы, а также финансовые расчеты. Он упрощает
вычисления, заменяя умножение и деление сложением и вычитанием, что было
особенно важно до появления электронных калькуляторов, и до сих пор служит
мощным инструментом в астрономии, физике, биологии и других областях.
7

9.

“Колледж менеджмента”
Логарифмы в науке
Выполнила
студентка
группы 25 О/П:
Ковязина А.Д