Обьединение_и_пересечение_событий

1. Обьединение и пересечение событий

Смирнов Матвей
Бажутов Даниил
Праск Максим

2.

• Цель урока:Узнать об Обьединении и пересечении
• Вопросы урока: что это и с чем это едят?

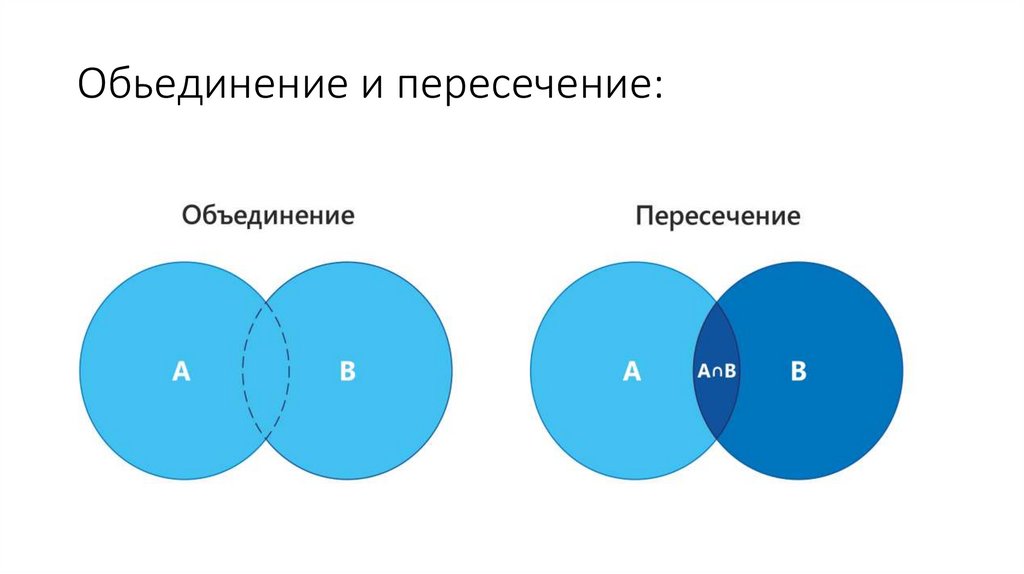
3. Обьединение и пересечение:

4.

Пересечение событий - это событие, которое происходит, если
одновременно происходят оба события. Например, если событие A —
это выпадение чётного числа на кубике, а событие B — выпадение числа
больше 3, то A∩B — это выпадение числа 4 или 6.
Объединение событий - это событие, которое происходит, если хотя
бы одно из событий происходит. Например, если событие A — это
выпадение чётного числа, а событие B — выпадение числа меньше 4,
то A∪B — это выпадение числа 1, 2, 3 или 6.
На диаграмме Эйлера-Венна:
•Пересечение - это область, где круги пересекаются
•Объединение - это вся область, покрытая кругами

5.

6.

7.

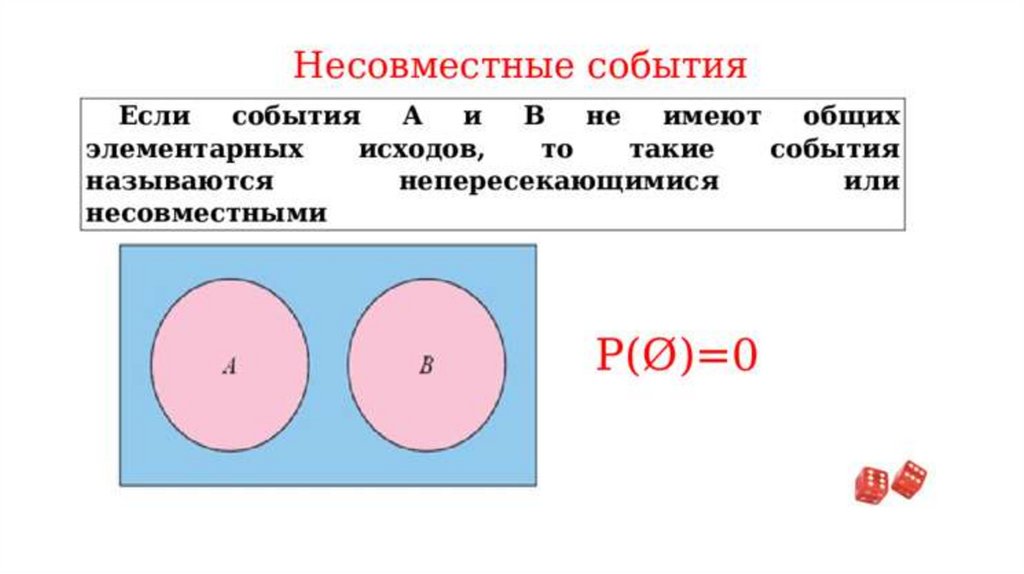
• Несовместимые события — это события, которые не могут
произойти одновременно. Например, при подбрасывании
монеты невозможно, чтобы одновременно выпали и орёл, и
решка. Если одно из событий происходит, другое обязательно не
происходит.
• На диаграмме Эйлера-Венна несовместимые события
изображаются непересекающимися кругами. Например, если
событие A — это выпадение чётного числа на кубике, а
событие B — выпадение числа 1, то эти события несовместимые,
так как число 1 не является чётным.

8.

9.

• Леонард Эйлер —
выдающийся швейцарский
математик и механик XVIII
века, чьи работы оказали
огромное влияние на
развитие математики,
физики и механики. Одним
из его значимых вкладов
является диаграмма
Эйлера-Венна, которая
используется для
визуализации отношений
между множествами.

10.

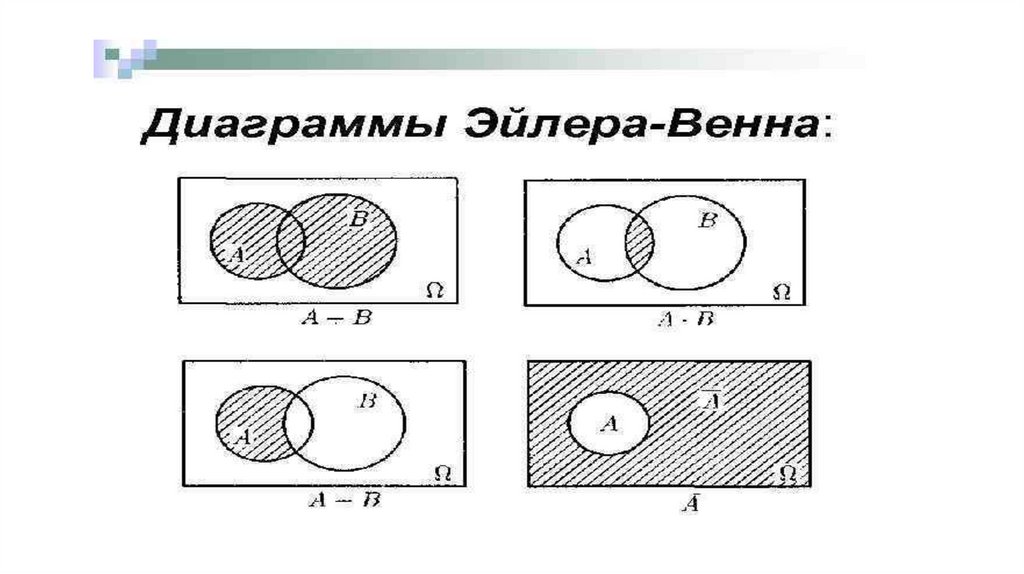
• Диаграмма Эйлера-Венна представляет собой графическое
изображение множеств в виде кругов, где пересечения кругов
показывают общие элементы между множествами. Эта диаграмма
помогает наглядно решать задачи на пересечение, объединение и
разность множеств.
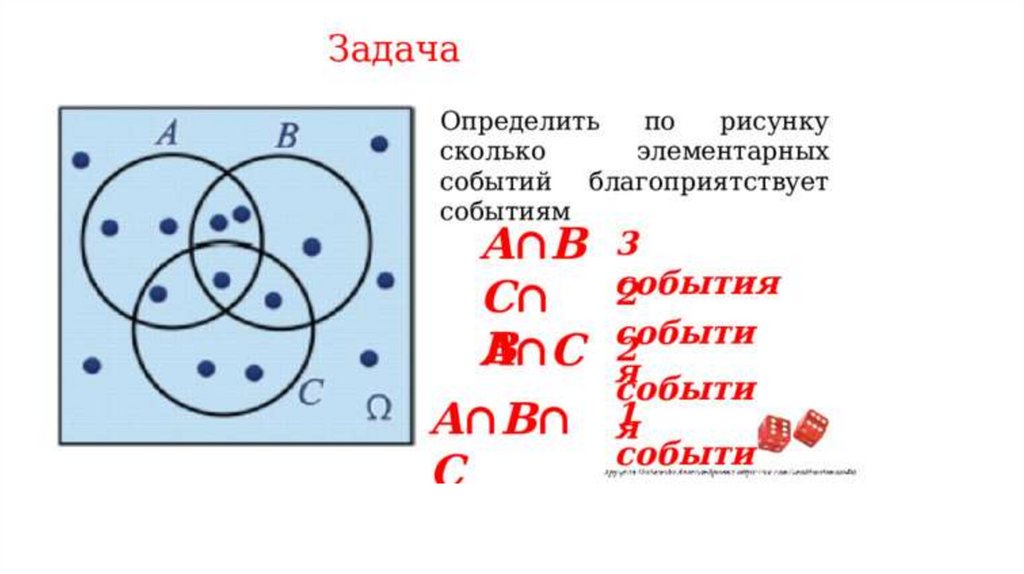
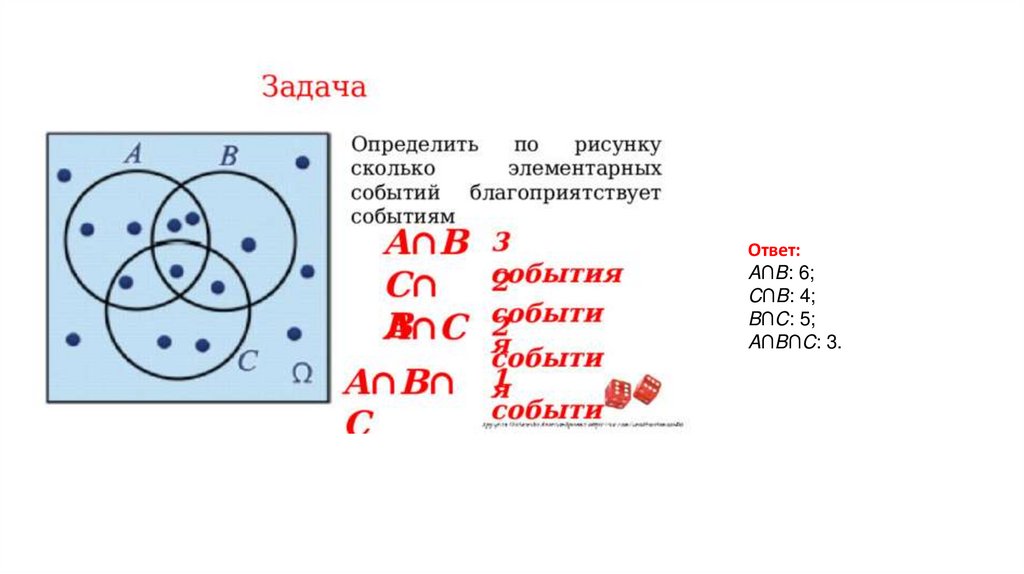
• На изображении представлена задача, где нужно определить
количество элементарных событий, благоприятствующих различным
событиям. Например:
• A∩B — пересечение множеств A и B, то есть элементы, которые
принадлежат обоим множествам.
• C∩A — элементы множества C, которые не принадлежат множеству A.
• B∩C — пересечение множеств B и C.
• A∩B∩C — элементы, которые одновременно принадлежат всем трём
множествам.

11.

12.

13.

Ответ:
A∩B: 6;
C∩B: 4;
B∩C: 5;
A∩B∩C: 3.

14.

15. Итого:

• Узнали об обьединении и пересечении.
• Узнали об Леонарде Эйлере, и о его диограммах