КОМБИНАТОРИКА 3-4 КЛАСС - окт25

1. КОМБИНАТОРИКА

2.

С задачами, в которых
приходилось выбирать те
или
иные
предметы,
располагать
их
в
определенном порядке и
отыскивать среди разных
расположений наилучшие,
люди столкнулись ещё в
доисторическую
эпоху,
выбирая
оружие
и
наилучшее
положение
охотников во время охоты,
воинов - во время битвы,
инструментов - во время
работы.

3.

Комбинаторика – как ветвь науки математики, изучающая
комбинации и перестановки предметов, возникла в XVII веке.

4.

Комбинаторика – раздел математики, в которой изучаются
вопросы о том, сколько различных комбинаций,
подчинённых тем или иным условиям, можно составить из
данных объектов.
Особая примета комбинаторных задач – это вопрос,
который можно сформулировать таким образом, что он
начинался бы словами:
- Сколькими способами…?
- Сколько вариантов…?
Термин «комбинаторика» происходит от латинского
слова «combina», что в переводе на русский означает –
«сочетать», «соединять»

5.

Рассмотрим и запишем в тетради несколько задач.
Задача.
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 1 и 2.
Решение с помощью схемы
В записи числа на первом месте (в разряде сотен) может стоять цифра 1 или 2
На втором месте (в разряде десятков) в каждом случае также может стоять одна
из двух цифр 1 или 2

6.

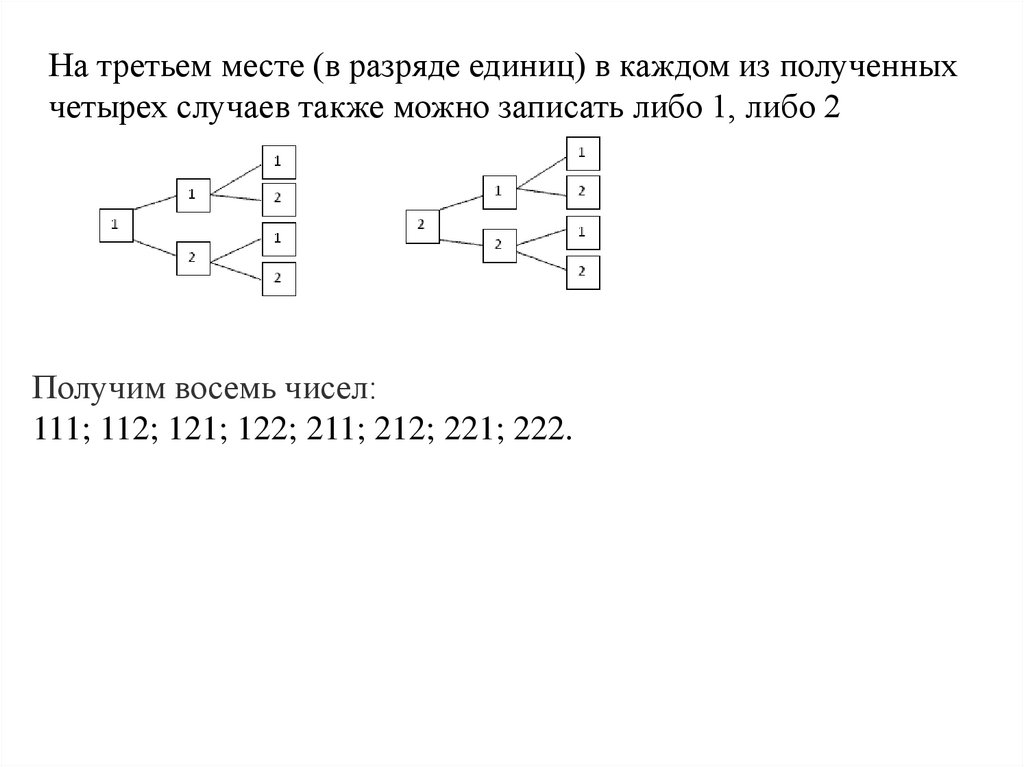
На третьем месте (в разряде единиц) в каждом из полученных
четырех случаев также можно записать либо 1, либо 2
Получим восемь чисел:
111; 112; 121; 122; 211; 212; 221; 222.

7.

Пример 1. Ученики Олеся, Марианна и Данила делят между
собой красную, зелёную и фиолетовую конфеты. Сколько
вариантов распределения конфет у них может получиться?
Решение: Посмотрим, сколько разных вариантов конфет может
попасть к Олесе. Их целых три. Допустим, Олеся выбрала один из
них. Теперь очередь Марианны. У неё уже только два варианта для
выбора, потому что количество конфет уменьшилось после того,
как Олеся взяла себе одну. А у Данилы будет только один вариант
выбрать конфету - он просто возьмёт оставшуюся.
Поскольку при любом из трёх возможных вариантов взять
конфету у Олеси, у Марианны есть 2 варианта, а у Данилы 1,
можно выразить общее количество вариантов в виде
произведения: 3*2*1 = 6.
Итого, у ребят есть 6 различных способов разделить эти
конфеты между собой по одной.

8.

В зависимости от понимания значения слова «распределить»,
задачу можно было решать и по-другому. Например, предоставив
одному из учеников все три конфеты, а остальным – ни одной.
Тогда возможных вариантов было бы три.
Так же слово «распределить» можно понять с той точки
зрения, что одному ученику достаётся 2 конфеты, другому – одна,
а третьему – ни одной. В таком случае возможных вариантов
было бы 6.
И, наконец, случай, при котором каждому ученику достаётся
по одной конфете (если нам не важно, какая это именно конфета),
всего один.
Итого, всего 10 различных вариантов без учёта порядка
конфет.
Ответ: 10 различных вариантов

9.

Промежуточный итог.
Важно понимать, что именно в таких задачах понимается
слово «распределить»
Если бы в задаче было условия распределения каждому
ученику по одной конфете, то ответ был бы 6 вариантов.

10.

Пример 2. У Элеоноры 30 различных
карандашей и 40 различных ручек.
Сколько у неё существует способов
выбрать карандаш и ручку?
Решение: Заметим, что карандаши, как и ручки, различны.
Сколько можно составить пар с одним конкретным
карандашом?
К одному карандашу можно выбрать любую из сорока ручек.
Но таких карандашей 30.
Значит, общее количество способов выбрать пару составляет:
30*40=1200.
Ответ: 1200 способов

11.

В предыдущем примере для решения задачи
мы применили
правило умножения,
если элемент A можно выбрать n способами, и
при любом выборе A элемент B можно выбрать
m способами, то пару (A, B) можно выбрать
n·m способами.

12.

Пример 3. У мамы есть 5 различных карандашей, 6 различных
ручек и 4 различных фломастера. Сколькими способами она сможет
выбрать для сына два предмета с разными названиями?

13.

Пример 3. У мамы есть 5 различных карандашей, 6 различных
ручек и 4 различных фломастера. Сколькими способами она сможет
выбрать для сына два предмета с разными названиями?
Решение: Посмотрим на комбинацию «карандаш-ручка». Для
этой комбинации способов: 5*6 = 30.
Для комбинации «ручка-фломастер»: 6*4 = 24.
И, наконец, третья комбинация «карандаш-фломастер», дает 5*4
= 20 способов.
Общее количество вариантов получается сложением всех
способов, полученных в каждом из случаев: 30+24+20=74.
Ответ: 74 способа

14.

Решение предыдущего примера кажется
довольно простым, но содержит в себе
применение очень важного правила правила сложения:
если элемент A можно выбрать n способами, а
элемент B можно выбрать m способами, то
выбрать A или B можно n + m способами.

15.

16.

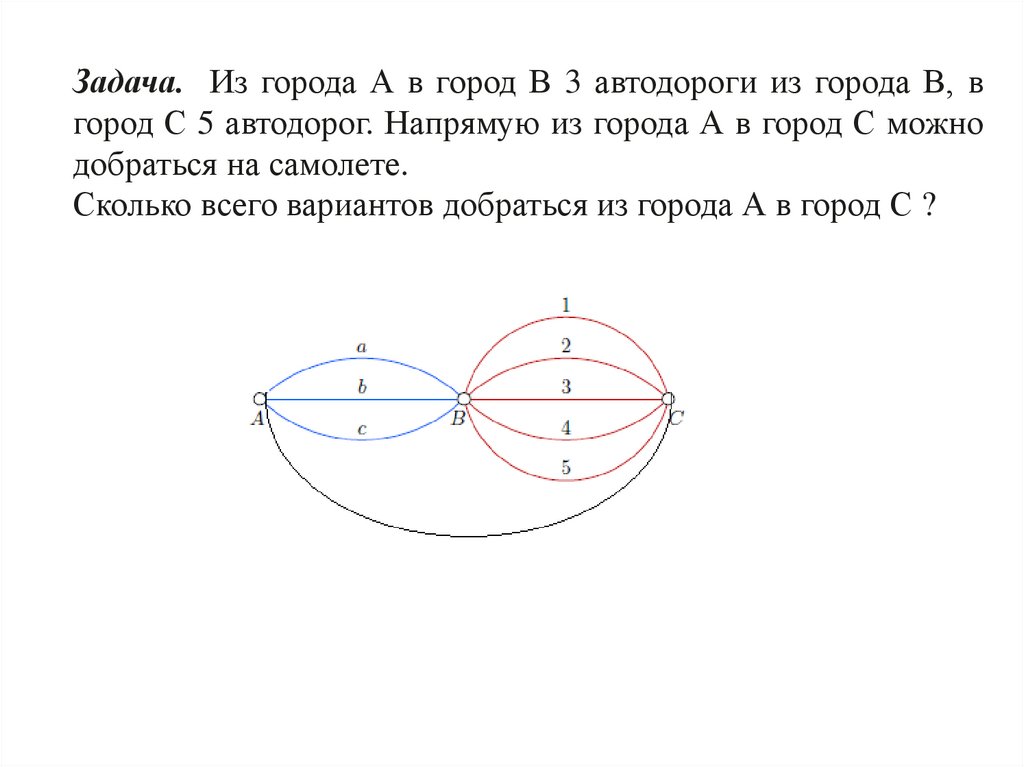
Задача. Из города А в город В 3 автодороги из города В, в
город С 5 автодорог. Напрямую из города А в город С можно
добраться на самолете.
Сколько всего вариантов добраться из города А в город С ?

17.

Решение
3*5+1 = 16 вариантов

18.

Так же при решении этой задачи мы столкнулись с разбором
случаев.
Если в каких-то задачах так же необходим разбор случаев, то
общий ответ получится как сложение чисел, являющихся
ответами в каждом из случаев.
Главное, чтобы случаи не пересекались.

19.

Рассмотрим термин «случаи не пересекаются» на примере.
Пример 4. В премьер-лиге чемпионата России по футболу
принимает участие 16 команд. Сколько было сыграно игр в
первом круге, если каждая команда играет с каждой?
Решение: На первый взгляд, решение кажется совсем
простым. Всего 16 команд, каждая сыграла с каждой, значит, 15
матчей. Значит, всего было сыграно: 15*16=240 матчей. Однако,
при таком рассуждении есть некоторая трудность: каждая игра
учтена дважды: для первой команды, и для второй команды. Но
при этом игра была всего одна! Вот так и получилось
«пересечение случаев». Значит, правильными будут такие
рассуждения: (16*15):2=120 матчей.
«Пересечением случаев» будем называть вариант решения
задачи, в котором один и тот же случай учтён более, чем один раз.
Формула подсчета матчей/турниров в однокруговом
турнире равно n*(n-1)/2
Ответ: 120 матчей

20.

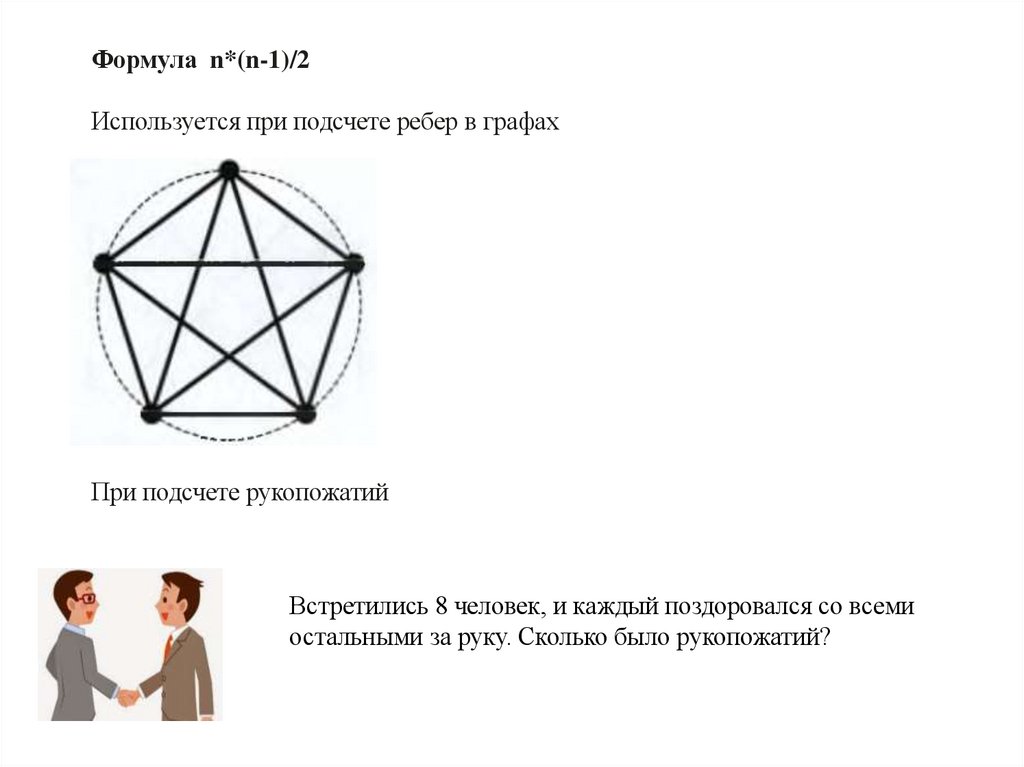
Формула n*(n-1)/2
Используется при подсчете ребер в графах
При подсчете рукопожатий
Встретились 8 человек, и каждый поздоровался со всеми
остальными за руку. Сколько было рукопожатий?

21.

Ответ
Если встретились 8 человек, то каждый здоровается с остальными четверыми: 8
7 = 56 (рукопожатий). При этом каждое рукопожатие мы посчитали дважды, а оно
было одно на двоих, значит, всего было 56/2=28рукопожатий.
Ответ:
8 человек - 28 рукопожатий.

22.

В некотором царстве было 6 городов, расположенных по
кругу. Каждые два города соединяла дорога. Сколько дорог
было в царстве?

23.

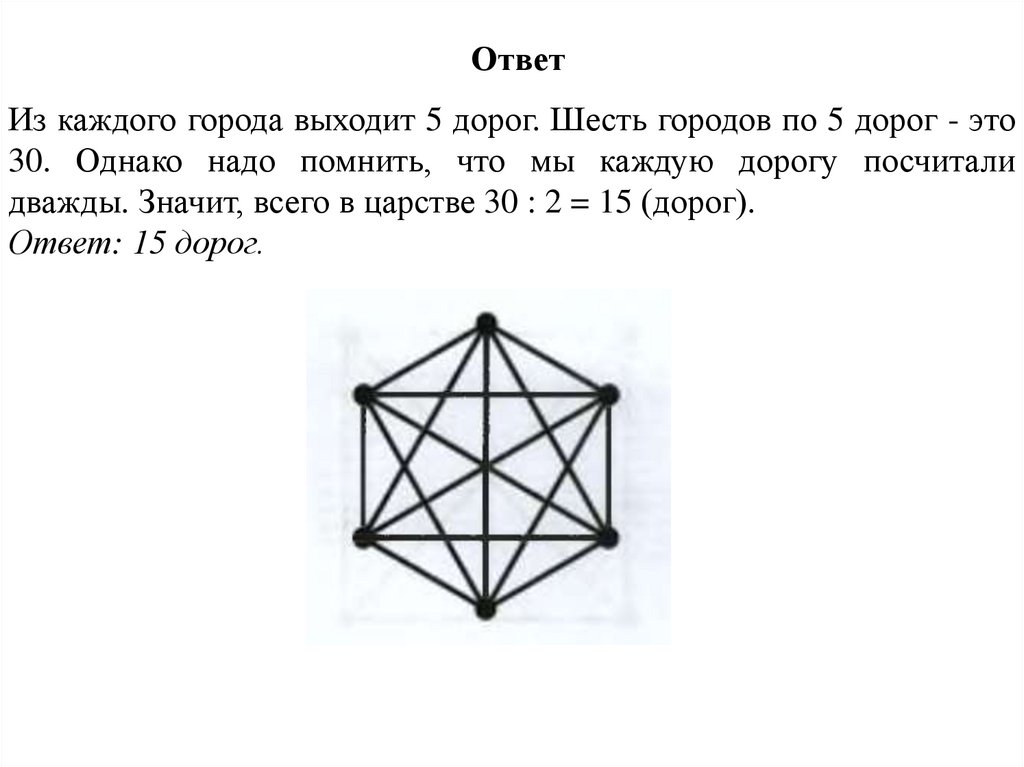
Ответ
Из каждого города выходит 5 дорог. Шесть городов по 5 дорог - это
30. Однако надо помнить, что мы каждую дорогу посчитали
дважды. Значит, всего в царстве 30 : 2 = 15 (дорог).
Ответ: 15 дорог.

24.

В стране 9 городов. Каждые
два
города
соединяет
авиалиния.
Сколько
авиалиний в стране?

25.

Ответ
Из каждого города выходит 8 авиалиний. Так как все города
соединены попарно это ребра в графах, считаем с помощью
Формулы n*(n-1)/2=9*(9-1)/2=72
Девять городов по 8 дорог - это 72. Однако надо помнить,
что мы каждую дорогу посчитали дважды. Значит, всего
авиалиний 72 : 2 = 36 .
Ответ: 36 авиалиний в стране.

26.

Пол, Джон и Том делали самолётики. Каждый запустил в
каждого. Сколько всего было сделано самолётиков, если
мальчики кидали только свои самолётики?

27.

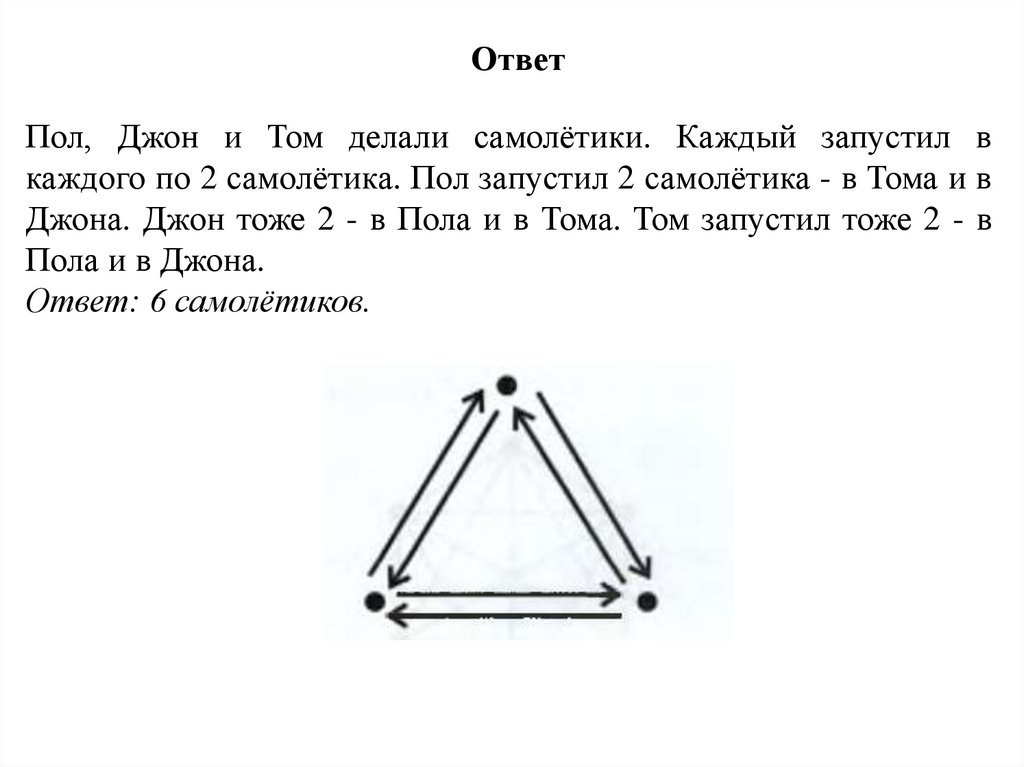
Ответ
Пол, Джон и Том делали самолётики. Каждый запустил в
каждого по 2 самолётика. Пол запустил 2 самолётика - в Тома и в
Джона. Джон тоже 2 - в Пола и в Тома. Том запустил тоже 2 - в
Пола и в Джона.
Ответ: 6 самолётиков.