laplacian-mesh-editing

1. Laplacian Surface Editing

INFORMATIK
Laplacian Surface Editing
Olga Sorkine
Daniel Cohen-Or Yaron Lipman
Tel Aviv University
Marc Alexa
TU Darmstadt
Christian Rössl Hans-Peter Seidel
Max-Planck Institut für Informatik

2. Differential coordinates

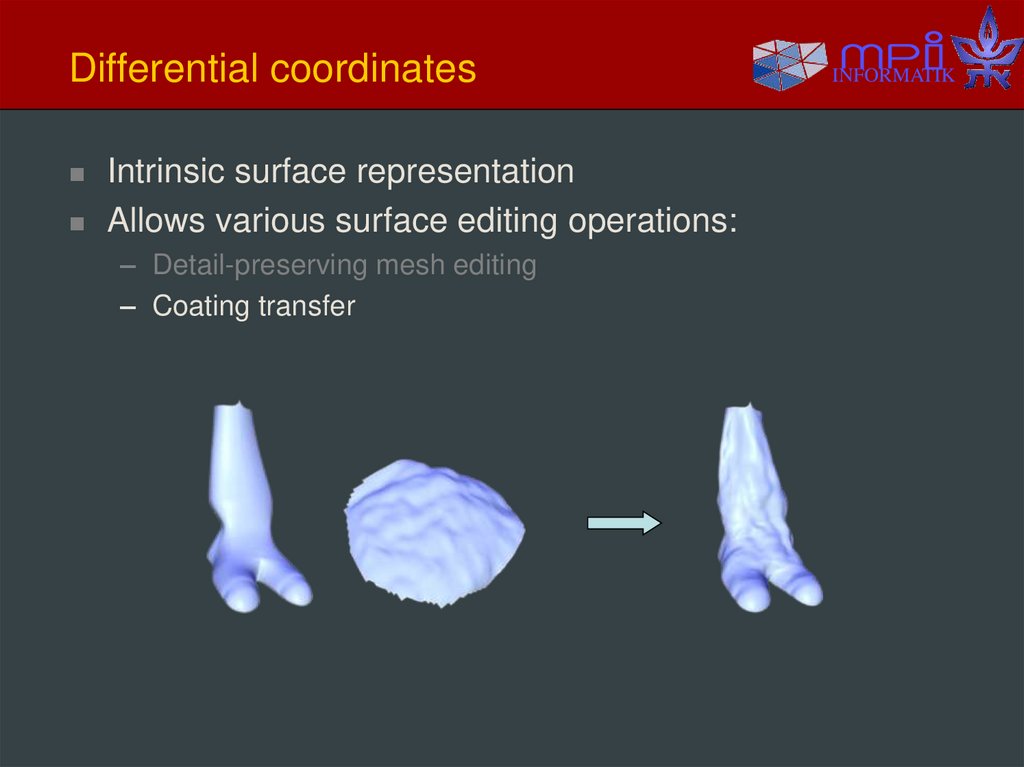
Intrinsic surface representation
Allows various surface editing operations:
– Detail-preserving mesh editing
INFORMATIK

3. Differential coordinates

Intrinsic surface representation
Allows various surface editing operations:
– Detail-preserving mesh editing
– Coating transfer
INFORMATIK

4. Differential coordinates

Intrinsic surface representation
Allows various surface editing operations:
– Detail-preserving mesh editing
– Coating transfer
– Mesh transplanting
INFORMATIK

5. What is it?

INFORMATIK
Differential coordinates are defined by the discrete
Laplacian operator:
1
δ i L( v i ) v i
vj
di j N (i )
For highly irregular meshes: cotangent weights [Desbrun et al. 99]
average of
the neighbors

6. Why differential coordinates?

INFORMATIK
They represent the local detail / local shape description
– The direction approximates the normal
– The size approximates the mean curvature
δi
1
vi v
di v N (i )
1
v i v ds
len( ) v
1
lim
vi v ds H ( vi ) ni
len ( ) 0 len( )
v

7. Why differential coordinates?

INFORMATIK
Local detail representation – enables detail preservation
through various modeling tasks
Representation with sparse matrices
Efficient linear surface reconstruction

8. Overall framework

INFORMATIK
Compute differential representation
L(V )
Pose modeling constraints
v i ui , i C
Reconstruct the surface – in least-squares sense
2
2
V arg min L(V ) v i ui
V
i C

9. Overall framework

ROI is bounded by a belt (static anchors)
Manipulation through handle(s)
INFORMATIK

10. Related work

INFORMATIK
Multi-resolution: [Zorin el al. 97], [Kobbelt et al. 98],
[Guskov et al. 99], [Boier-Martin et al. 04],
[Botsch and Kobbelt 04] 2
Laplacian smoothing: Taubin [SIGGRAPH 95]
Laplacian Morphing: Alexa [TVC 03]
Image editing: Perez et al. [SIGGRAPH 03]
Mesh Editing: Yu et al. [SIGGRAPH 04]

11. Problem: invariance to transformations

INFORMATIK
The basic Laplacian operator is translation-invariant, but
not rotation- and scale-invariant
Reconstruction attempts to preserve the original global
orientation of the details

12. Invariance – solutions

INFORMATIK
Explicit transformation of the differential coordinates prior
to surface reconstruction
– Lipman, Sorkine, Cohen-Or, Levin, Rössl and Seidel,
“Differential Coordinates for Interactive Mesh Editing“,
SMI 2004
• Estimation of rotations from naive reconstruction
– Yu, Zhou, Xu, Shi, Bao, Guo and Shum,
“Mesh Editing With Poisson-Based Gradient Field Manipulation“,
SIGGRAPH 2004
• Propagation of handle transformation to the rest of the ROI

13. Estimation of rotations

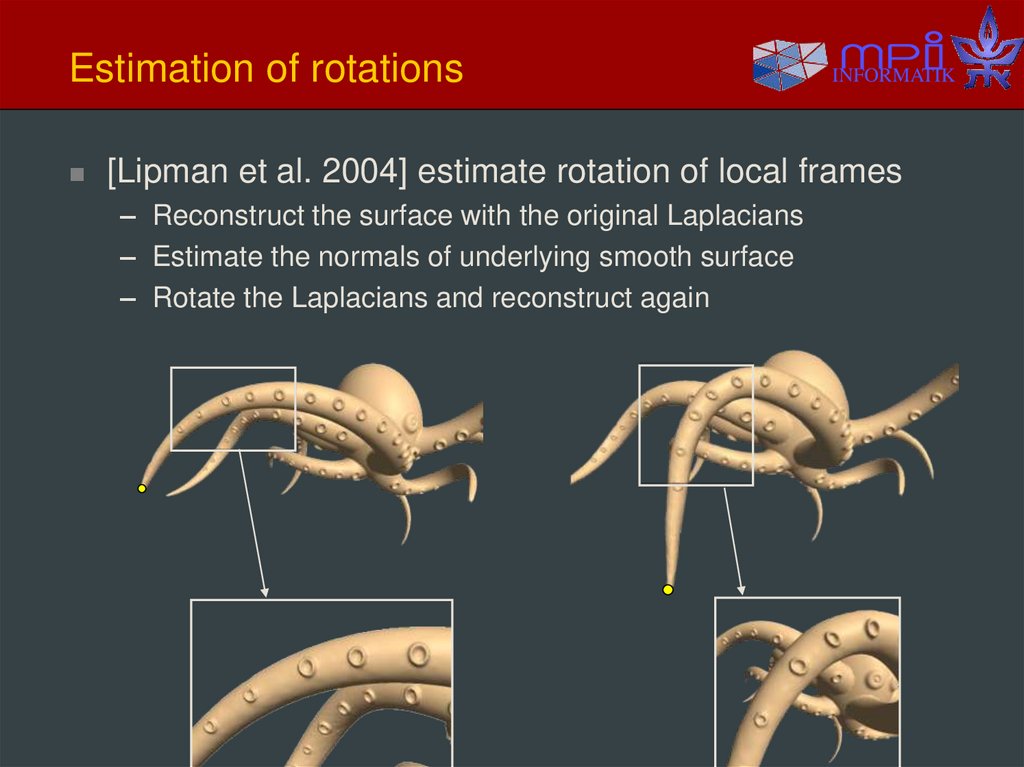
INFORMATIK
[Lipman et al. 2004] estimate rotation of local frames
– Reconstruct the surface with the original Laplacians
– Estimate the normals of underlying smooth surface
– Rotate the Laplacians and reconstruct again

14. Explicit assignment of rotations

INFORMATIK
Disadvantages:
– Heuristic estimation of the rotations
– Speed depends on the support of the smooth normal estimation
operator; for highly detailed surfaces it must be large
almost a height field
not a height field

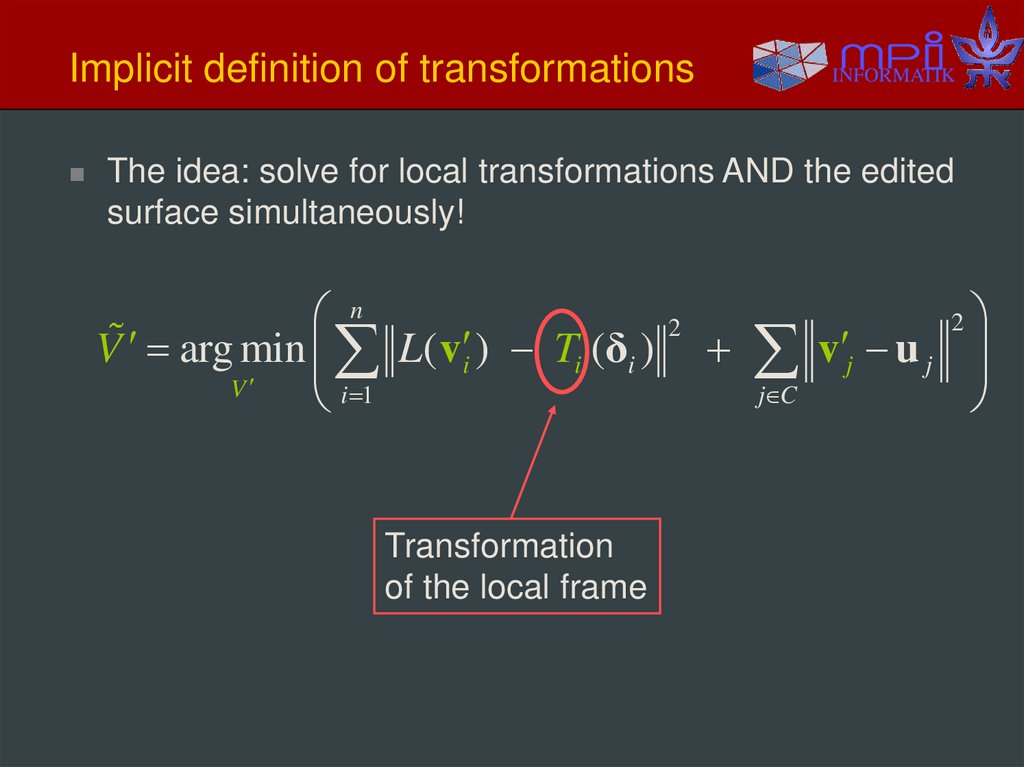
15. Implicit definition of transformations

INFORMATIK
The idea: solve for local transformations AND the edited
surface simultaneously!
n
2
2
V arg min L( v i ) Ti (δi ) v j u j
V
j C
i 1
Transformation
of the local frame

16. Defining the transformations Ti

INFORMATIK
n
2
2
V arg min L( v i ) Ti (δi ) v j u j
V
j C
i 1
How to formulate Ti ?
– Based on the local (1-ring) neighborhood
– Linear dependence on the unknown vi’
v i1 Ti v i1
Members of the 1-ring
of i-th vertex
v i2 Ti v i2
v ik Ti v ik
Ti

17. Defining the transformations Ti

INFORMATIK
First attempt: define Ti simply by solving
k
Ti arg min v i j Ti vi j
Ti
Ti
|
v i1
|
|
v i2
|
2
j 1
| |
v ik v i1
|
|
|
v i2
|
|
v ik
|

18. Defining the transformations Ti

INFORMATIK
Plug the expressions for Ti into the least-squares
reconstruction formula:
n
2
2
V arg min L( v i ) Ti δi v j u j
V
j C
i 1
Linear combination
of the unknown vi’

19. Constraining Ti

INFORMATIK
Trivial solution for Ti will result in membrane surface
reconstruction
To preserve the shape of the details we constrain Ti to
rotations, uniform scales and translations
t11
t21
Ti
t31
t41
t12
t22
t32
t42
t13 t14
t23 t24
t33 t34
t43 t44
Linear constraints on tlm
so that Ti is
rotation+scale+translation
??

20. Constraining Ti – 2D case

INFORMATIK
Easy in 2D:
s 0 0 cos
Ti 0 s 0 sin
0 0 1 0
sin
cos
0
d x w a tx
d y a w t y
1 0 0 1

21. Constraining Ti – 3D case

INFORMATIK
Not linear in 3D:
rotation +
T
s
exp
H
s
I
H
h
h
uniform scale
H is 3 3 skew-symmetric, Hx h x
Linearize by dropping the quadratic term

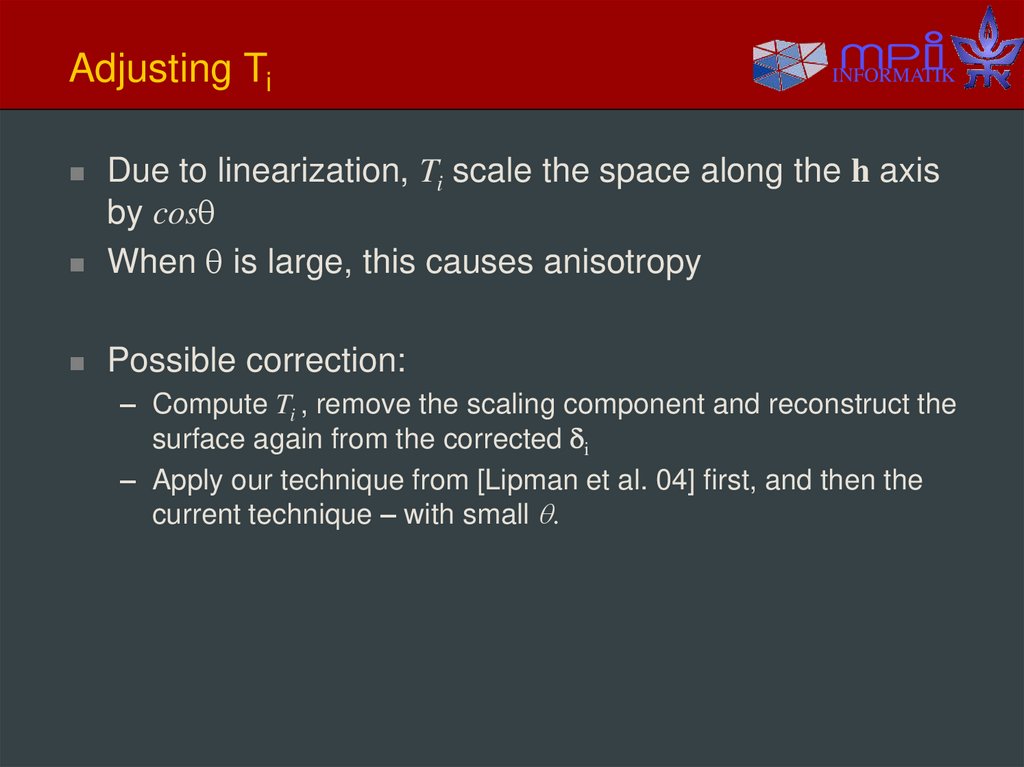
22. Adjusting Ti

INFORMATIK
Due to linearization, Ti scale the space along the h axis
by cos
When is large, this causes anisotropy
Possible correction:
– Compute Ti , remove the scaling component and reconstruct the
surface again from the corrected i
– Apply our technique from [Lipman et al. 04] first, and then the
current technique – with small .

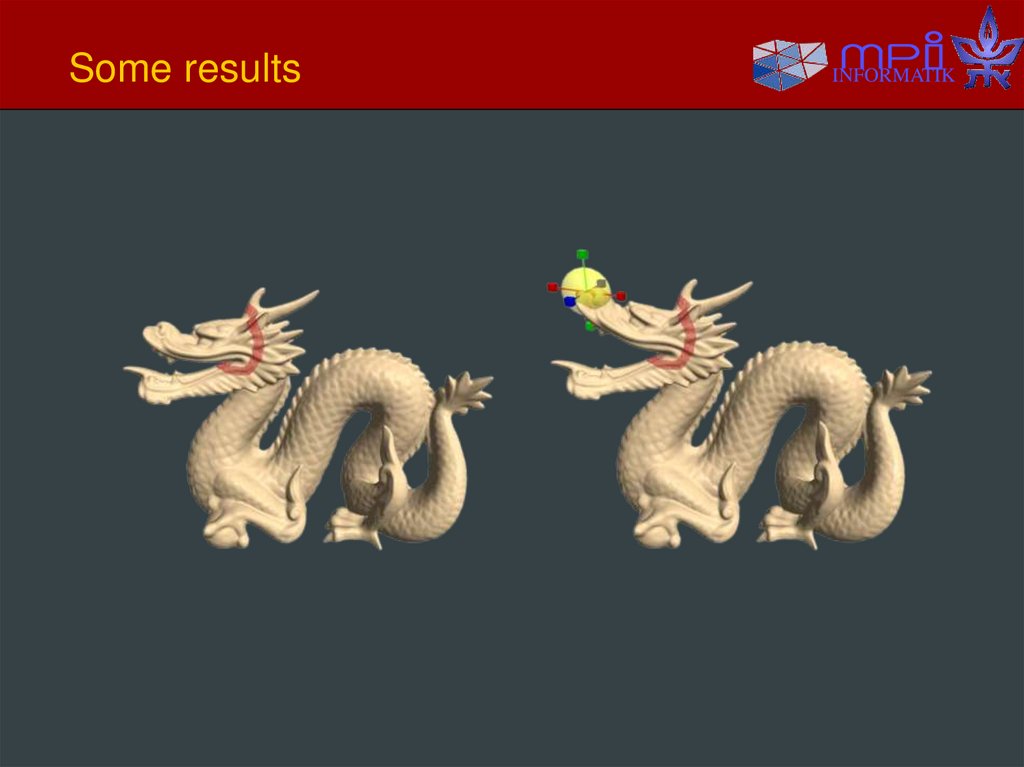
23. Some results

INFORMATIK

24. Some results

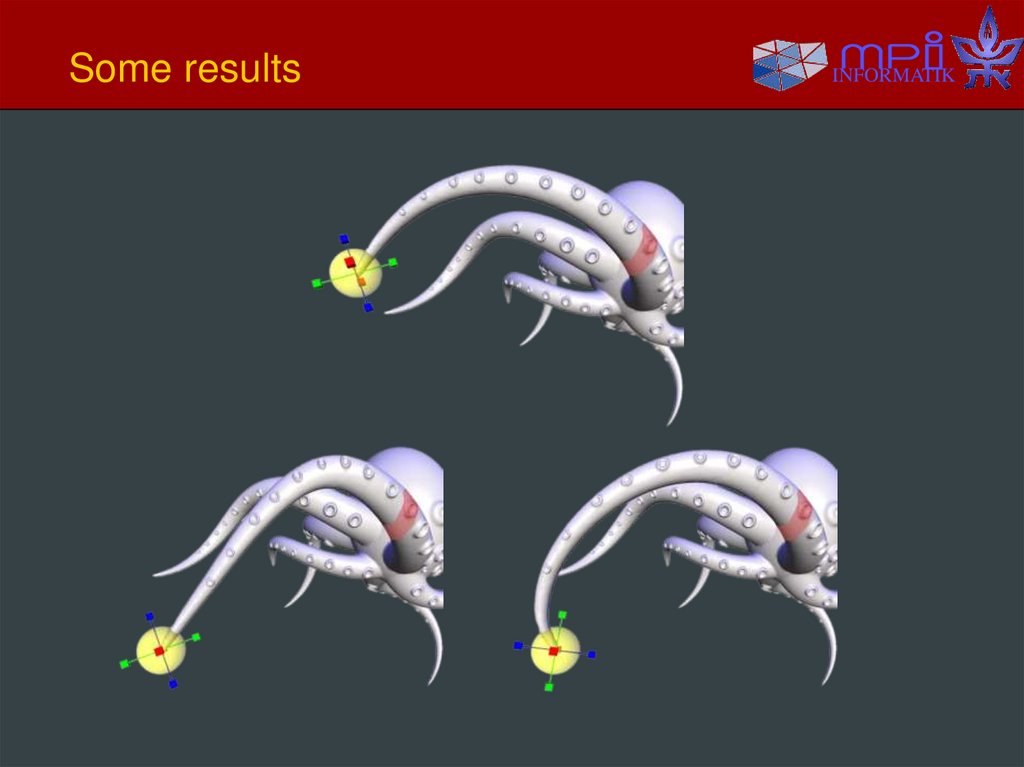
INFORMATIK

25. Some results

INFORMATIK

26. Some results

INFORMATIK

27. Some results

Video...
INFORMATIK

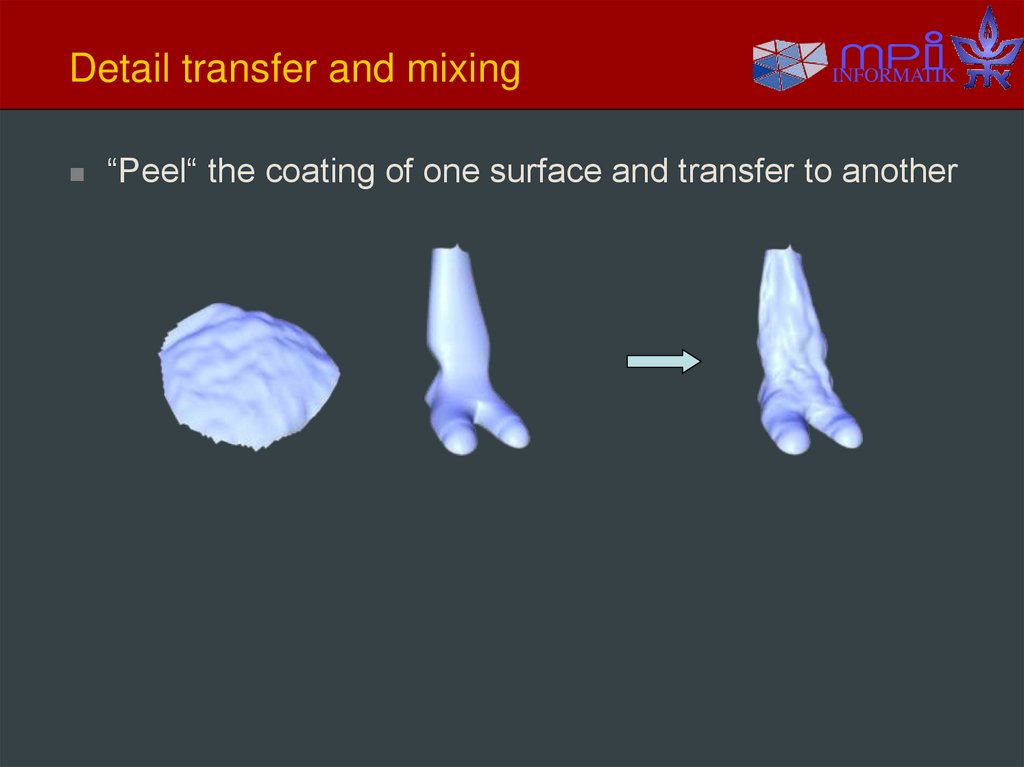
28. Detail transfer and mixing

INFORMATIK
“Peel“ the coating of one surface and transfer to another

29. Detail transfer and mixing

INFORMATIK
Correspondence:
– Parameterization onto a common domain and elastic warp to
align the features, if needed

30. Detail transfer and mixing

INFORMATIK
Detail peeling:
i
i
i i i
Smoothing by
[Desbrun et al.99]

31. Detail transfer and mixing

INFORMATIK
Changing local frames:
i
i

32. Detail transfer and mixing

Reconstruction of target surface from target :
target i i
INFORMATIK

33. Examples

INFORMATIK

34. Examples

INFORMATIK

35. Mixing Laplacians

Taking weighted average of i and ‘i
INFORMATIK

36. Mesh transplanting

The user defines
– Part to transplant
– Where to transplant
– Spatial orientation and scale
Topological stitching
Geometrical stitching via Laplacian mixing
INFORMATIK

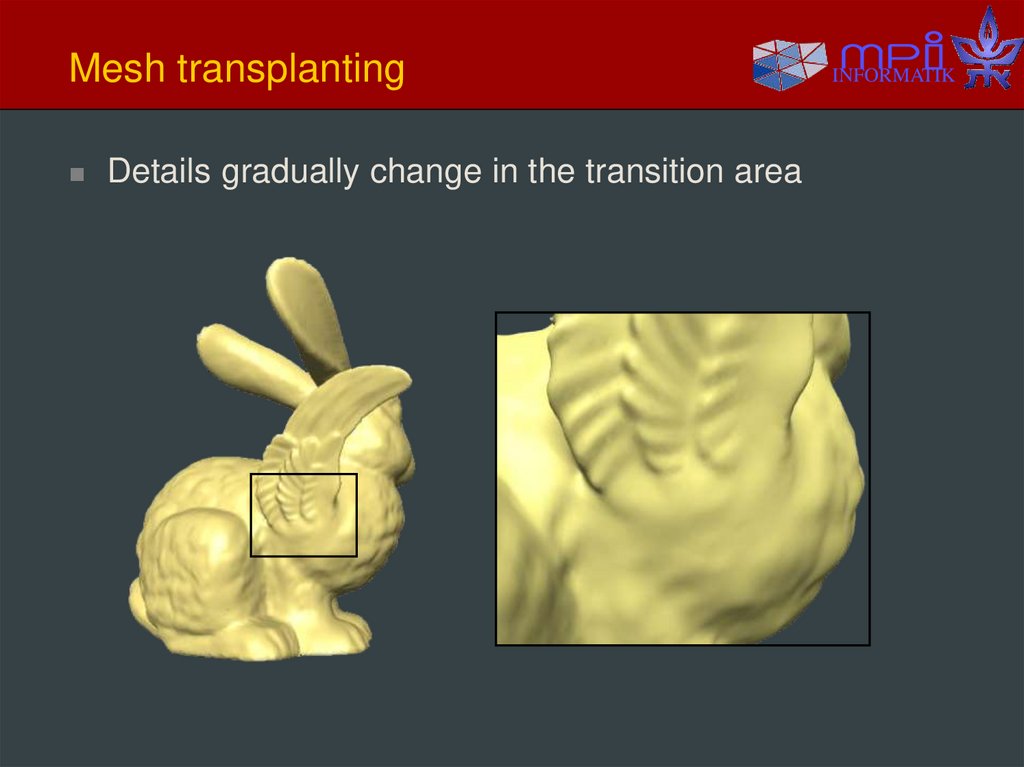
37. Mesh transplanting

Details gradually change in the transition area
INFORMATIK

38. Mesh transplanting

Details gradually change in the transition area
INFORMATIK

39. Conclusions

INFORMATIK
Differential coordinates are useful for applications that
need to preserve local details
Reconstruction by linear least-squares – smoothly
distributes the error across the domain
Linearization of 3D rotations was needed in order to
solve for optimal local transformations – can we do
better?

40. Acknowledgments

INFORMATIK
German Israel Foundation (GIF)
Israel Science Foundation (founded by the Israel
Academy of Sciences and Humanities)
Israeli Ministry of Science
Bunny, Dragon, Feline courtesy of Stanford University
Octopus courtesy of Mark Pauly

41. Thank you!

INFORMATIK
Thank you!

42. Gradual transition

INFORMATIK