Похожие презентации:
trigonometriya_funkcii_grafiki
1.
Математику нельзя изучать,наблюдая, как это делает сосед.
А.Нивен
2.
Тема урока:«Преобразование графиков
тригонометрических
функций»
3. Функция y=sin x, график и свойства.
1)D(y)=2)E(y)=
3)
4)sin(-x)=-sin x
5)Возрастает на
Убывает на
6)Периодичная
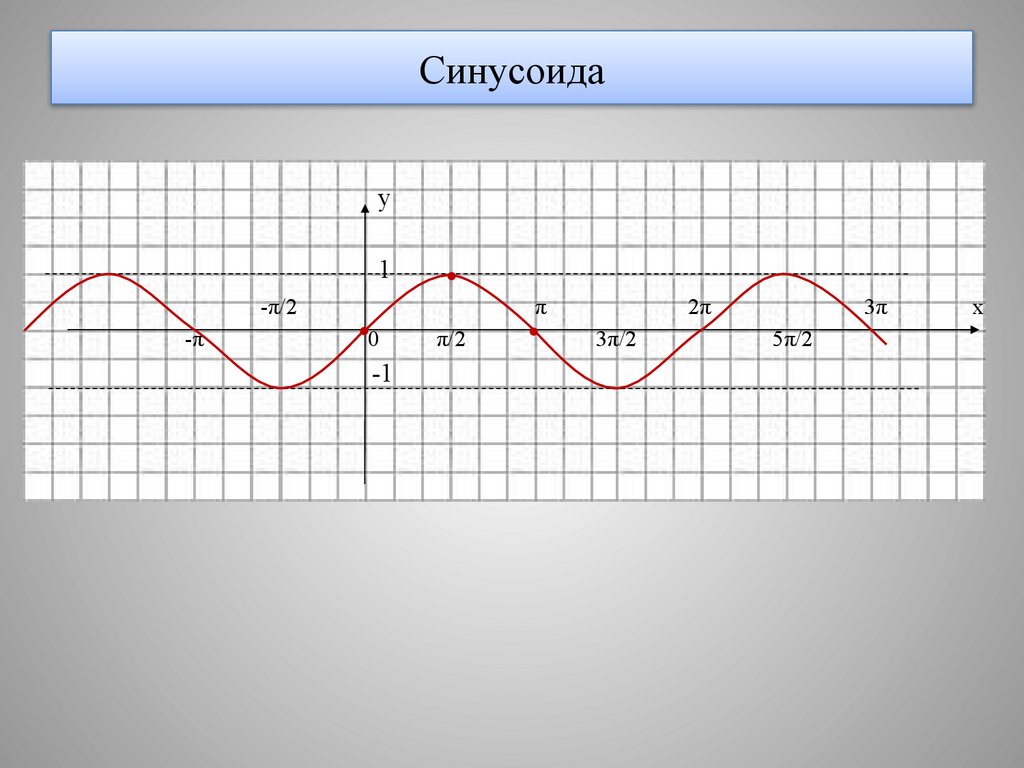
4. Синусоида
у1
-π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х
5. Функция y = cos x, её свойства и график.
1)D(y)=2)E(y)=
3)
4)cos(-x)=cosx
5)Возрастает на
Убывает на
6)Периодична
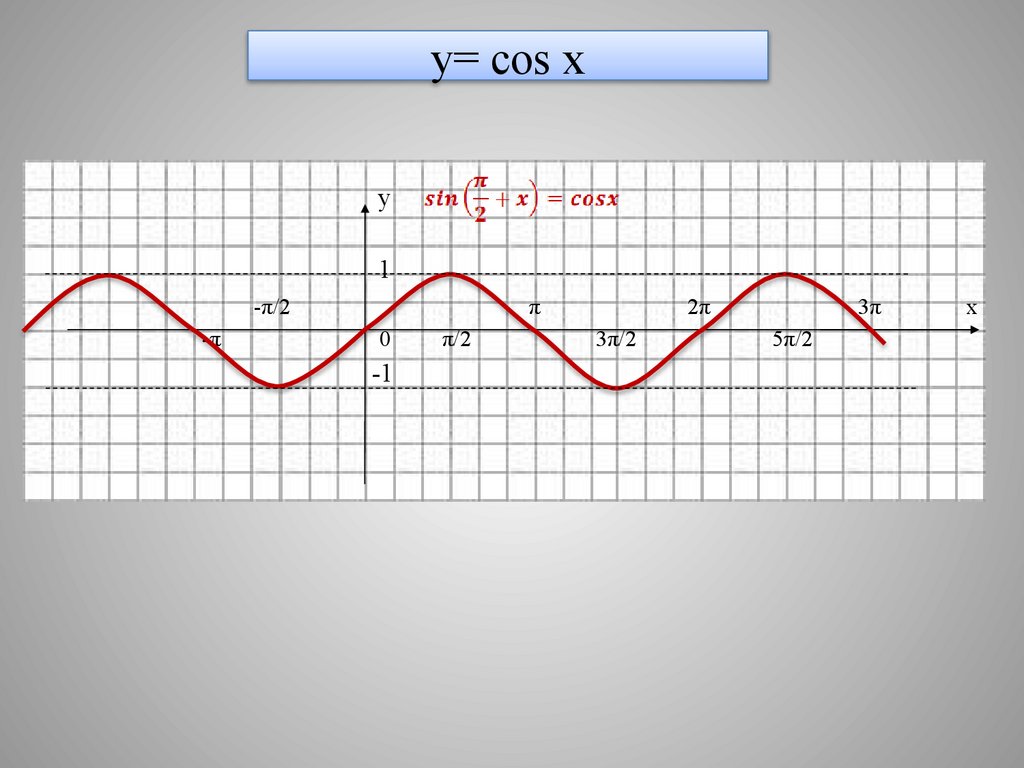
6. y= cos x
у1
-π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х
7. Функция y = tg x, её свойства и график
1.E(y)=2.D(y)=
3.tg(-x)=-tgx
4.Возрастает на
5.Периодичная
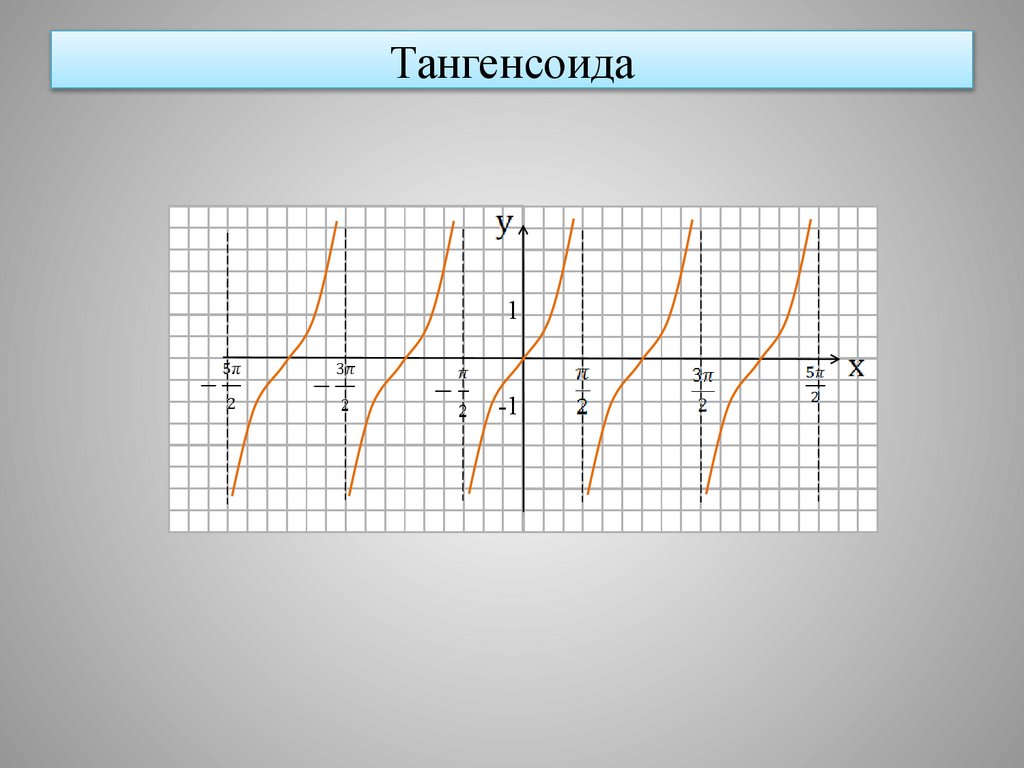
8. Тангенсоида
1-1
9.
1.Давайте вспомним известные вамалгоритмы построения графиков
функций вида :
у=f(х+р);
у=f(х)+m;
у=mf(x);
y=f(aх).
если известен график функции у=f(х)
10.
2. Какой масштаб мы выбралидля построения графиков
тригонометрических функций?
Почему?
3.Назовите ключевые точки,
которые мы наносим для построения
графиков тригонометрических
функций?
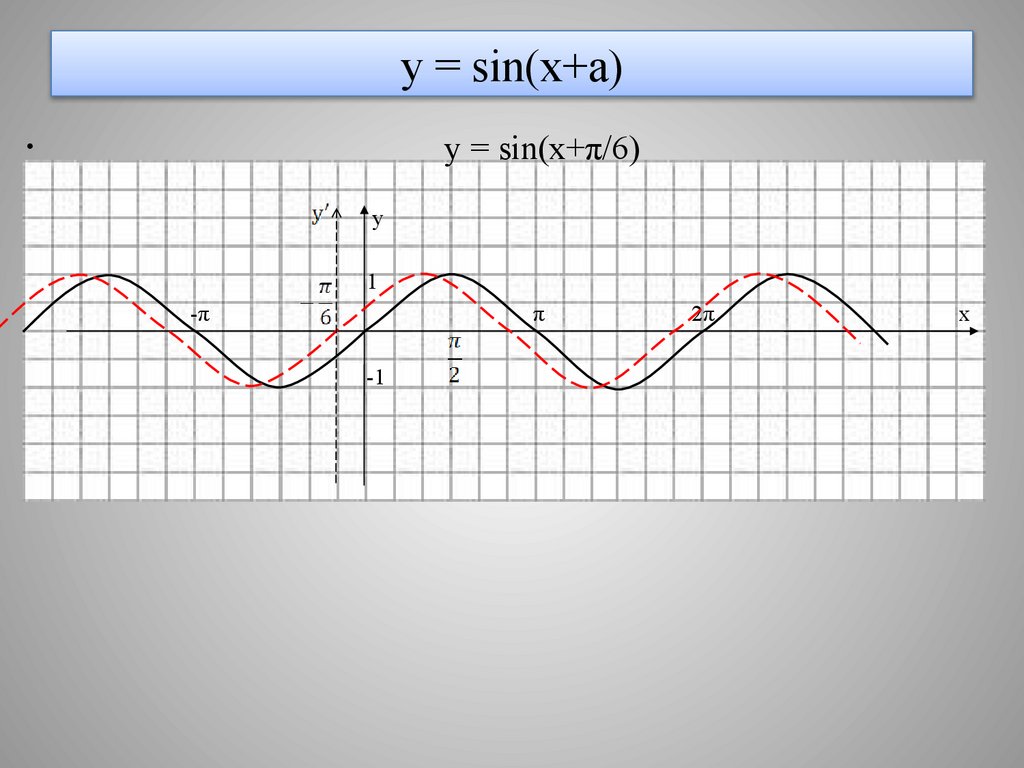
11. у = sin(x+a)
y = sin(x+π/6)y
1
-π
π
-1
2π
х
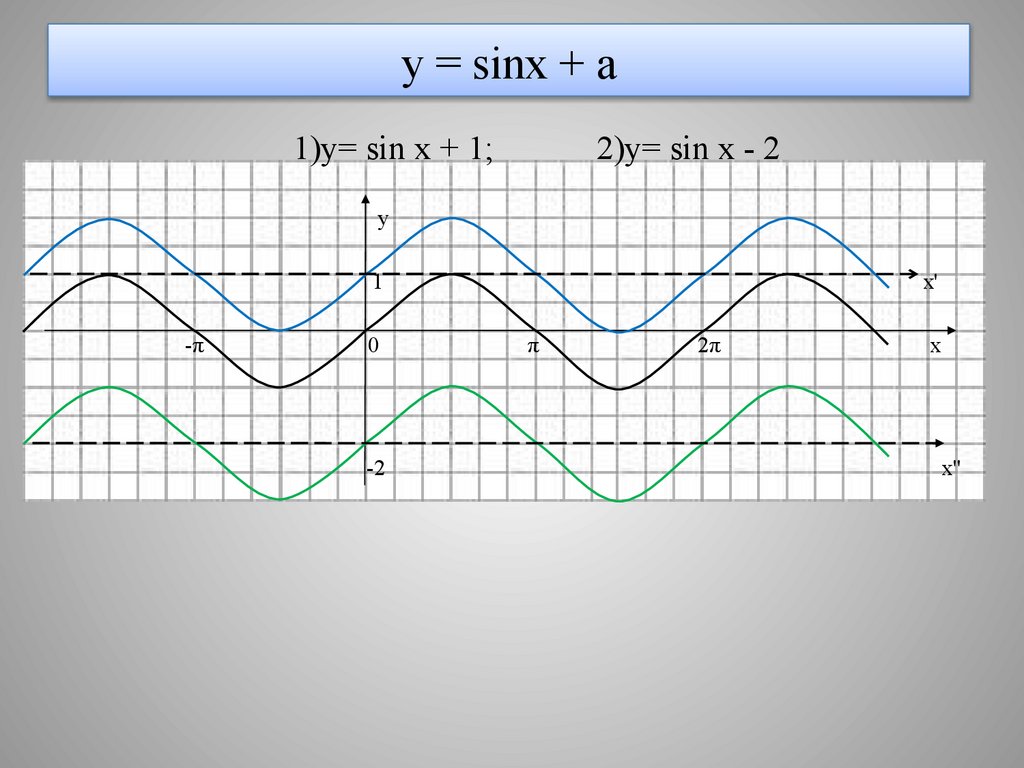
12. у = sinx + a
1)y= sin x + 1;2)y= sin x - 2
y
1
-π
0
-2
x'
π
2π
x
x''
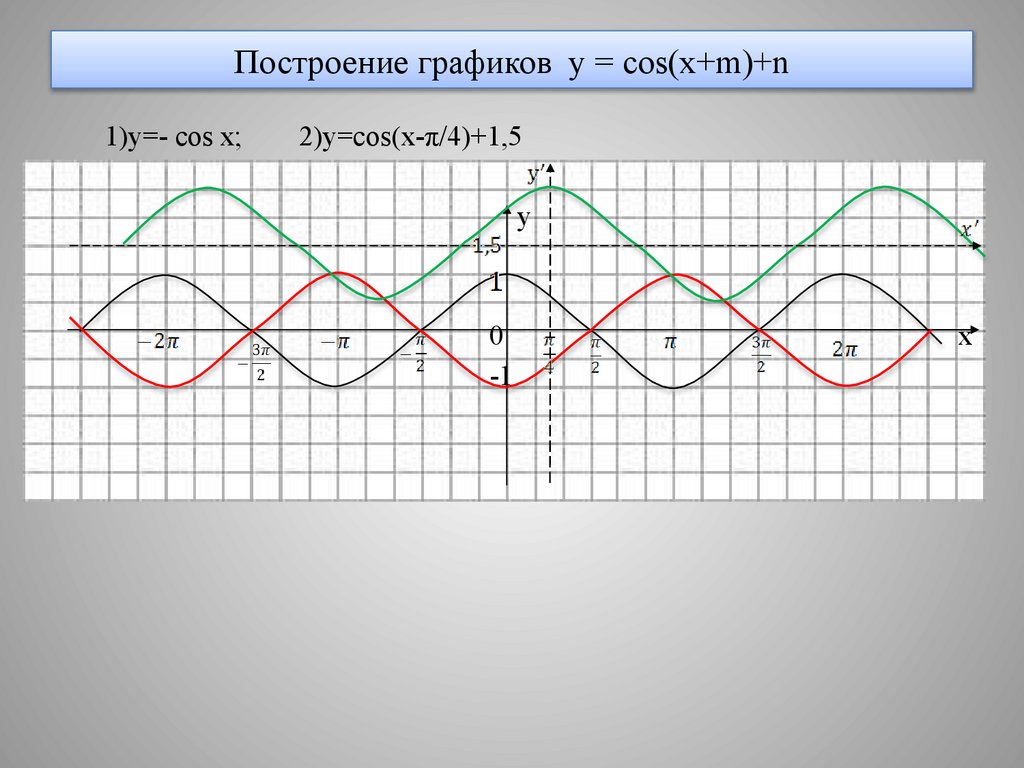
13. Построение графиков y = cos(x+m)+n
1)y=- cos x;2)y=cos(x-π/4)+1,5
y
0
-1
x
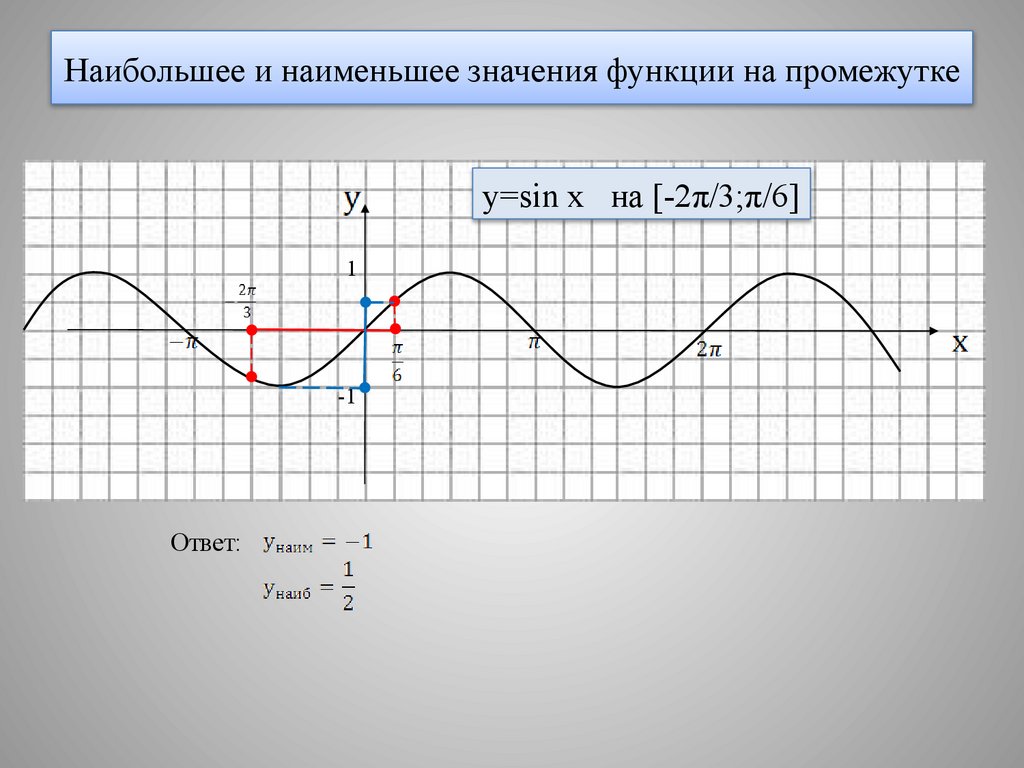
14. Наибольшее и наименьшее значения функции на промежутке
y=sin x на [-2π/3;π/6]1
-1
Ответ:
15.
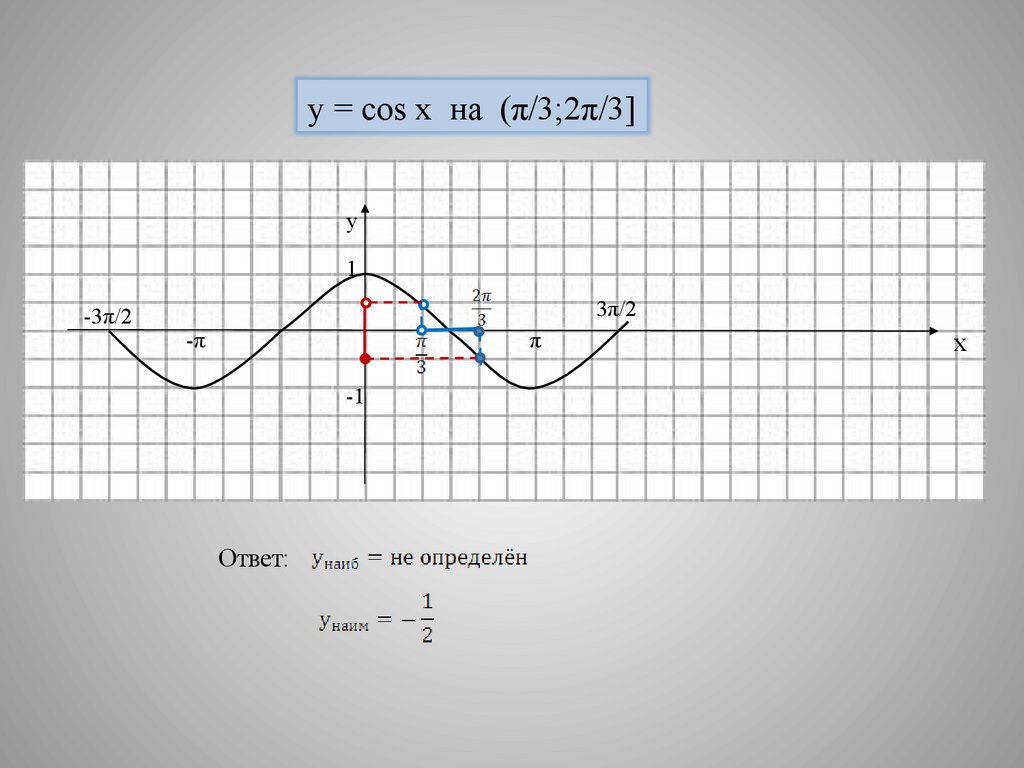
y = cos x на (π/3;2π/3]у
1
-3π/2
3π/2
-π
π
-1
Ответ:
х
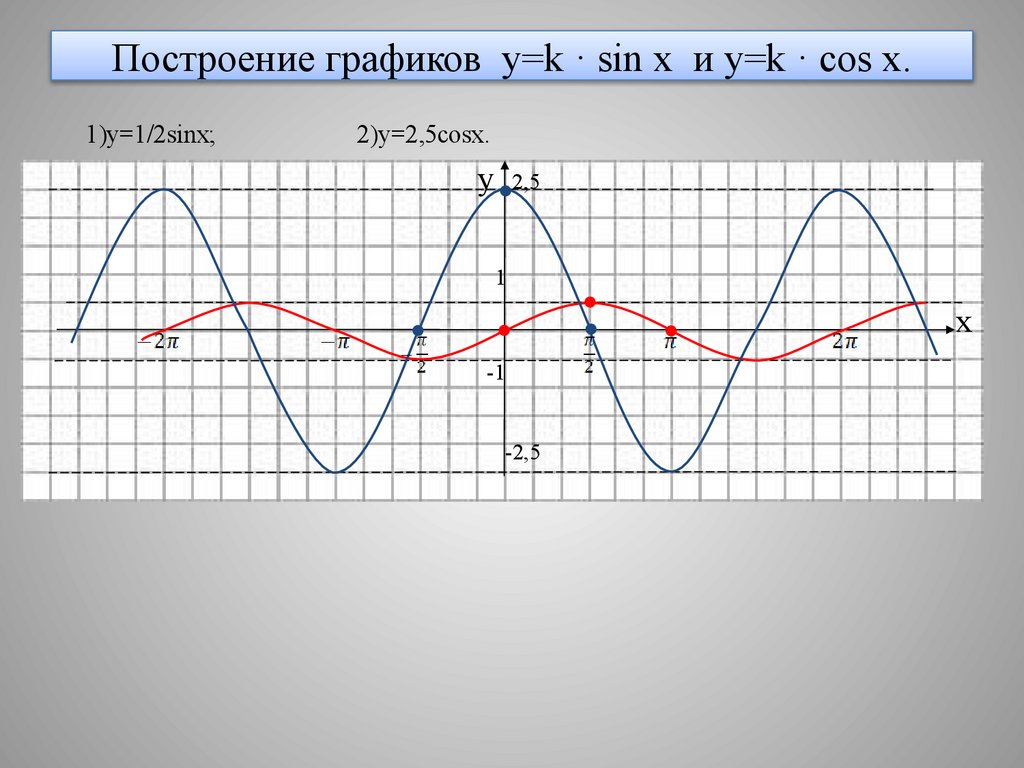
16. Построение графиков y=k · sin x и y=k · cos x.
1)y=1/2sinx;2)y=2,5cosx.
y 2,5
1
x
-1
-2,5
17. Найдите множество значений функции
1)y=sinx-3;2)y= cos(x+π/3);
3)y=sin(-2x+π)+1;
4)y=5cosx;
5)y= -sinx;
6)y=1/2cosx-3;
7)y=-4sin(x+1)+7;
18. Периодичность
Если y=f(x) периодичная с периодом Т₁‡0, тоy=A· f(kx+m)+B периодичная с периодом
Примеры:
1)
y=sin4x
Т₁=2π
2)
y=-4cos(x/3-1)+2
T₁=2π
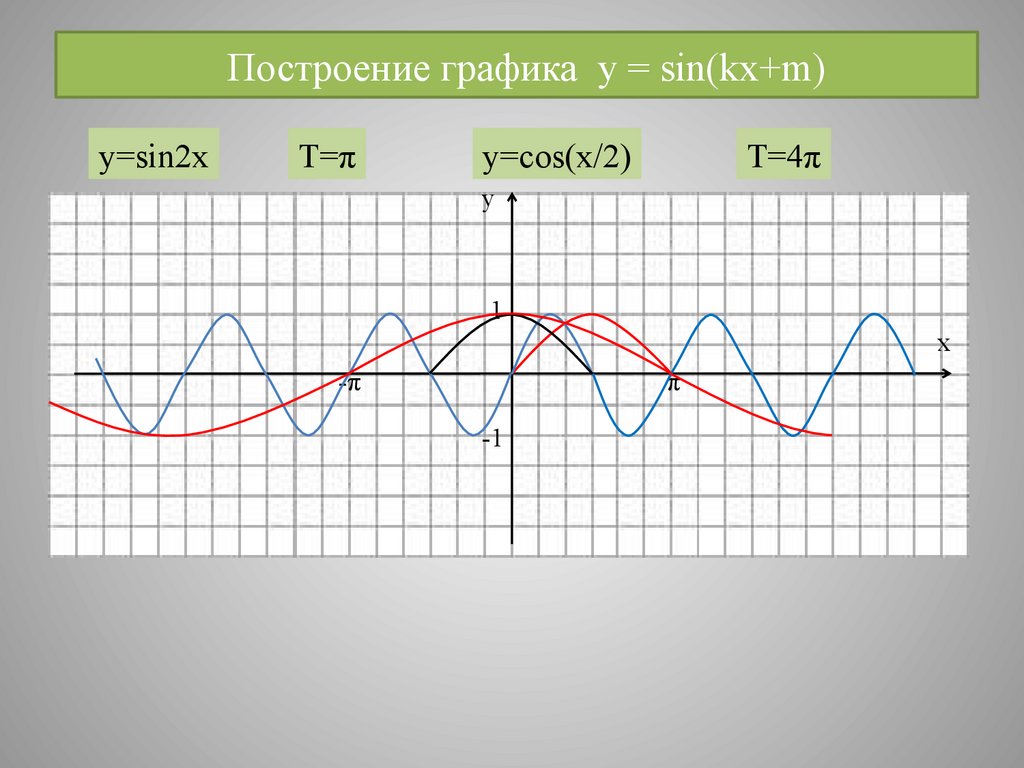
19. Построение графика y = sin(kx+m)
y=sin2xT=π
y=cos(x/2)
T=4π
у
1
х
-π
π
-1
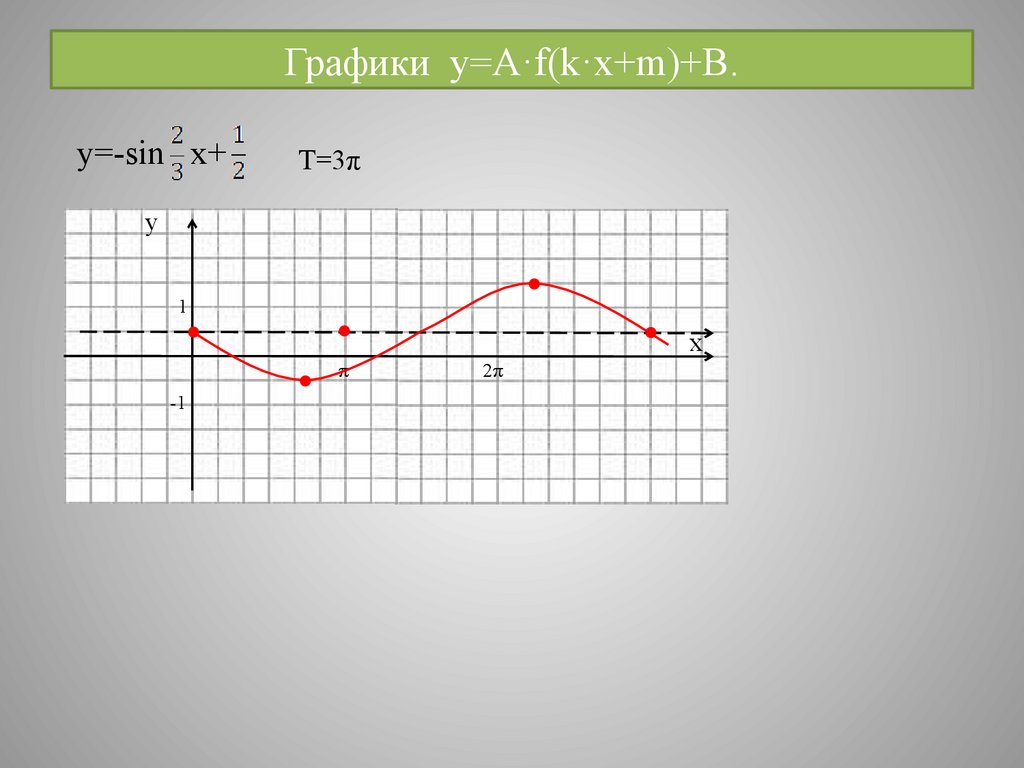
20. Графики y=A·f(k·x+m)+B.
y=-sin x+T=3π
y
1
x
π
-1
2π
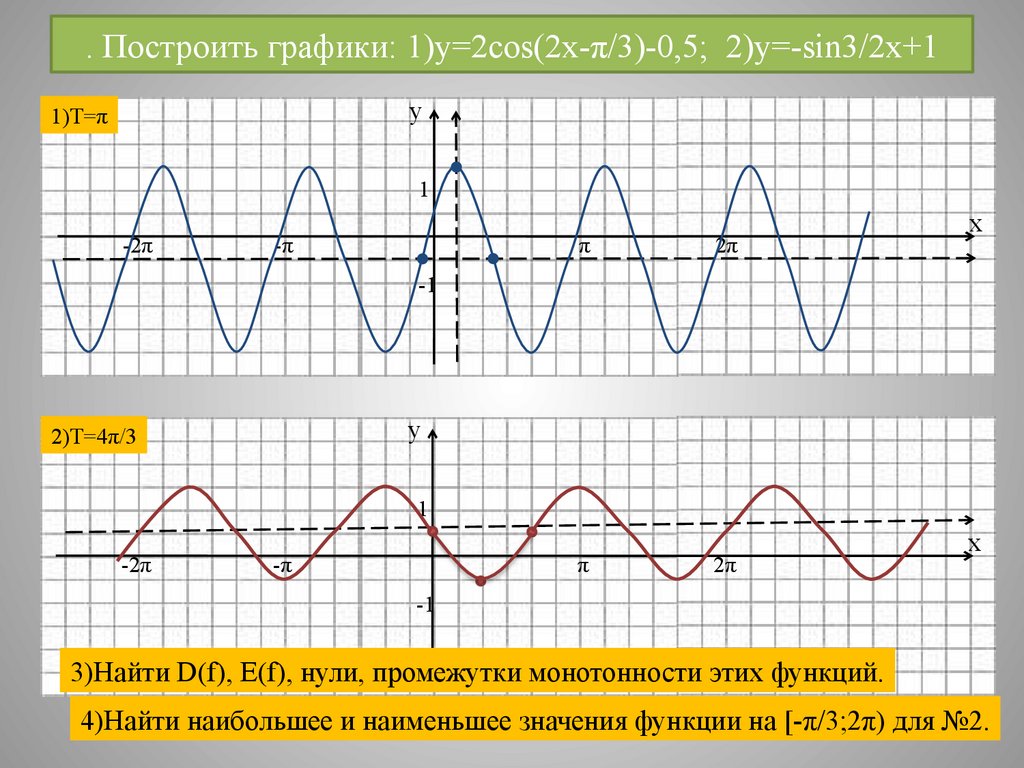
21. . Построить графики: 1)y=2cos(2x-π/3)-0,5; 2)y=-sin3/2x+1
у1)T=π
1
-2π
-π
π
2π
х
-1
у
2)T=4π/3
1
-2π
-π
π
2π
х
-1
3)Найти D(f), E(f), нули, промежутки монотонности этих функций.
4)Найти наибольшее и наименьшее значения функции на [-π/3;2π) для №2.
22.
23.
2 32
y
x
1
2
-1
2
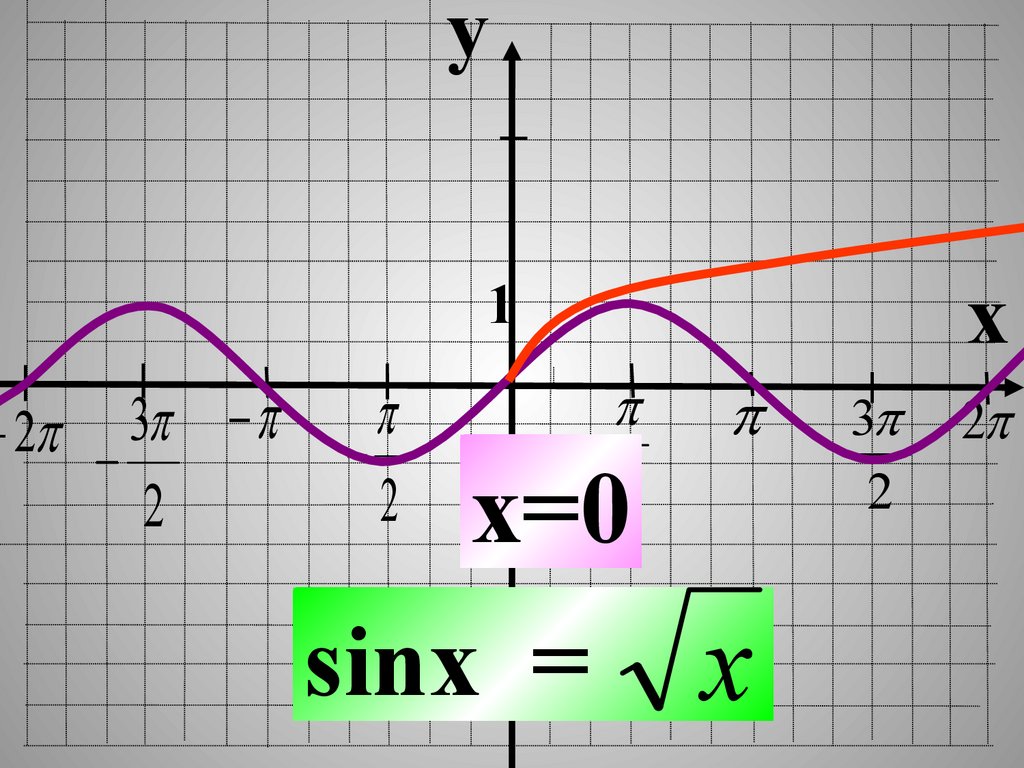
x=0
sinx = x
3
2
2
24.
yØ
2
2
3
2
1
-1
2
2
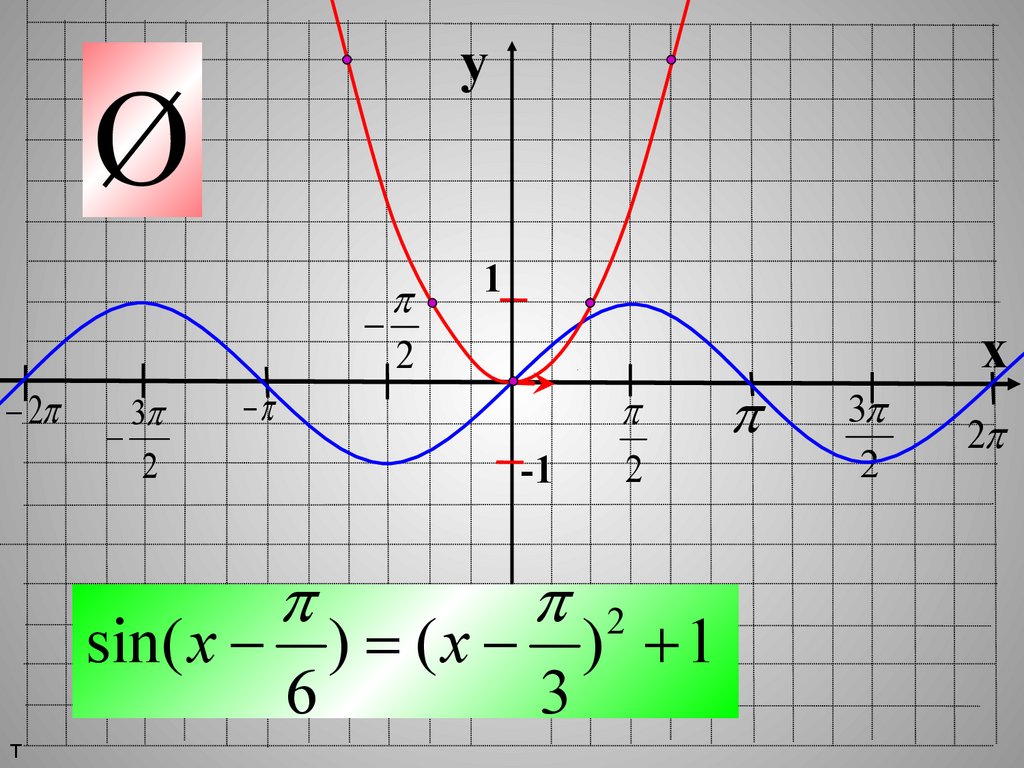
sin( x ) ( x ) 1
6
3
т
x
3
2
2
25.
yØ
2 3
2
x
1
2
-1
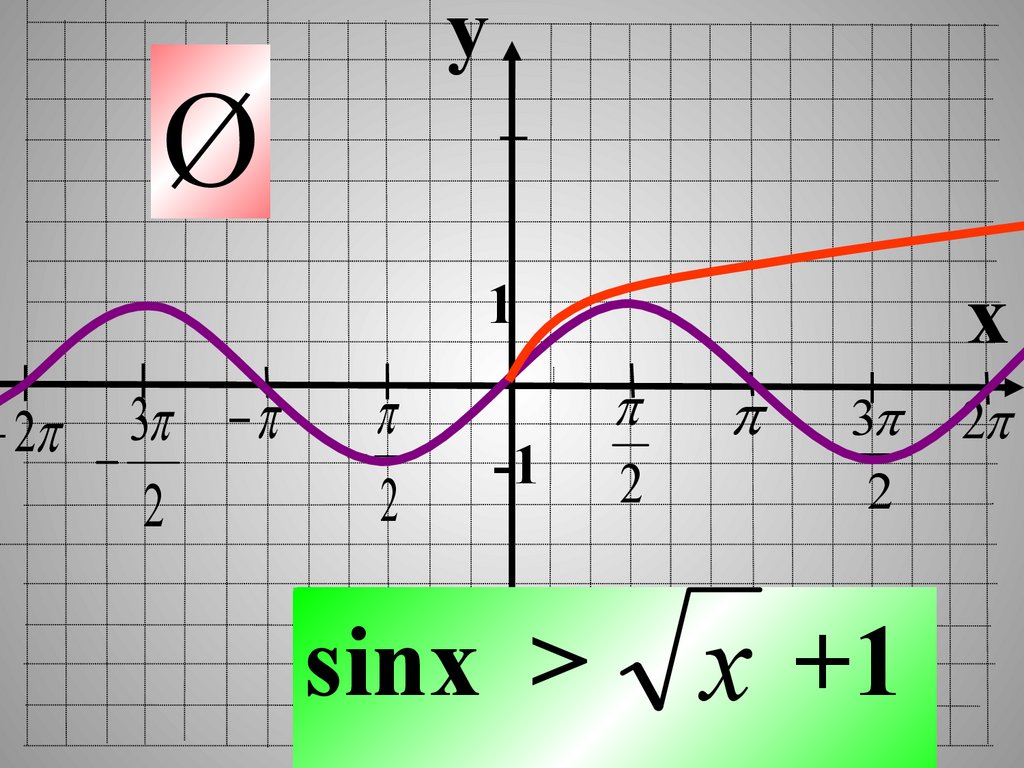
sinx >
2
3
2
x +1
2
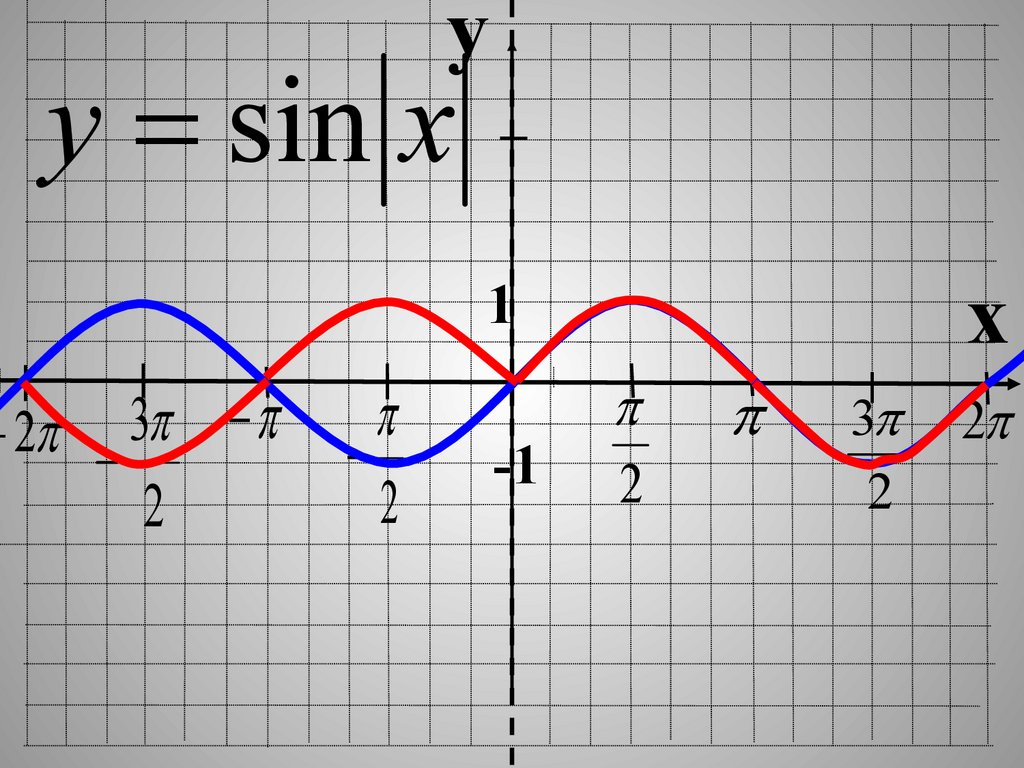
26.
yy sin x
y x 1
x [0; )
x
1
2 3
2
2
-1
sinx <
у
2
3
2
x +1
2
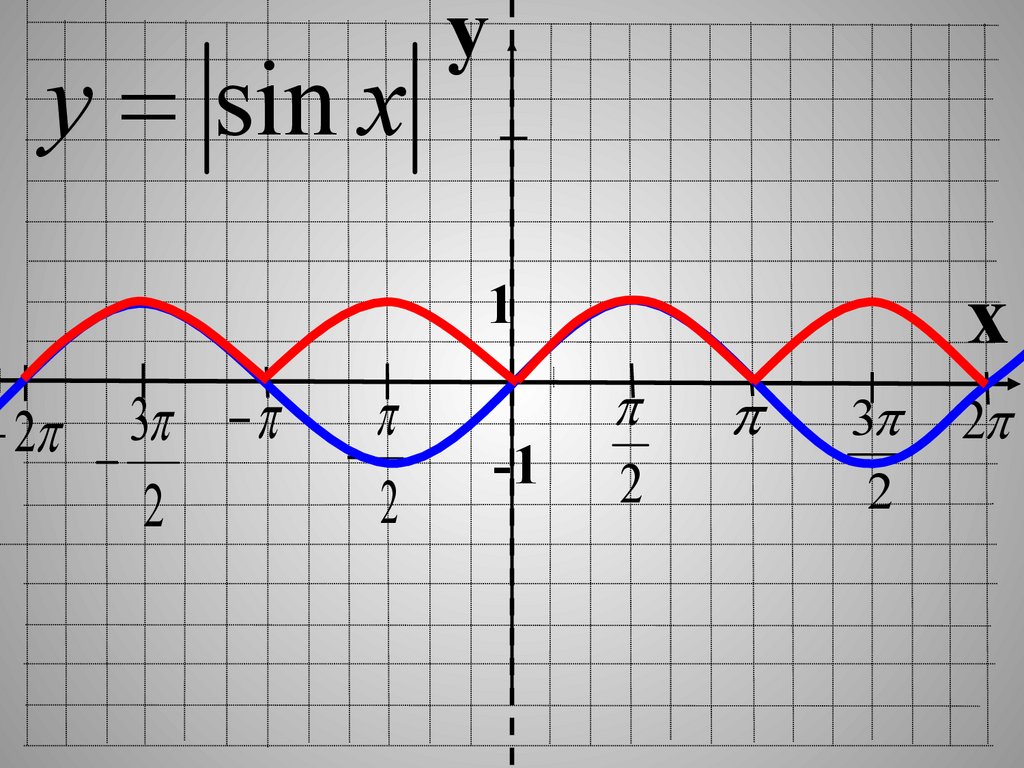
27.
y sin x2 3
2
y
x
1
2
-1
2
3
2
2
28.
yy sin x
2 3
2
x
1
2
-1
2
3
2
2
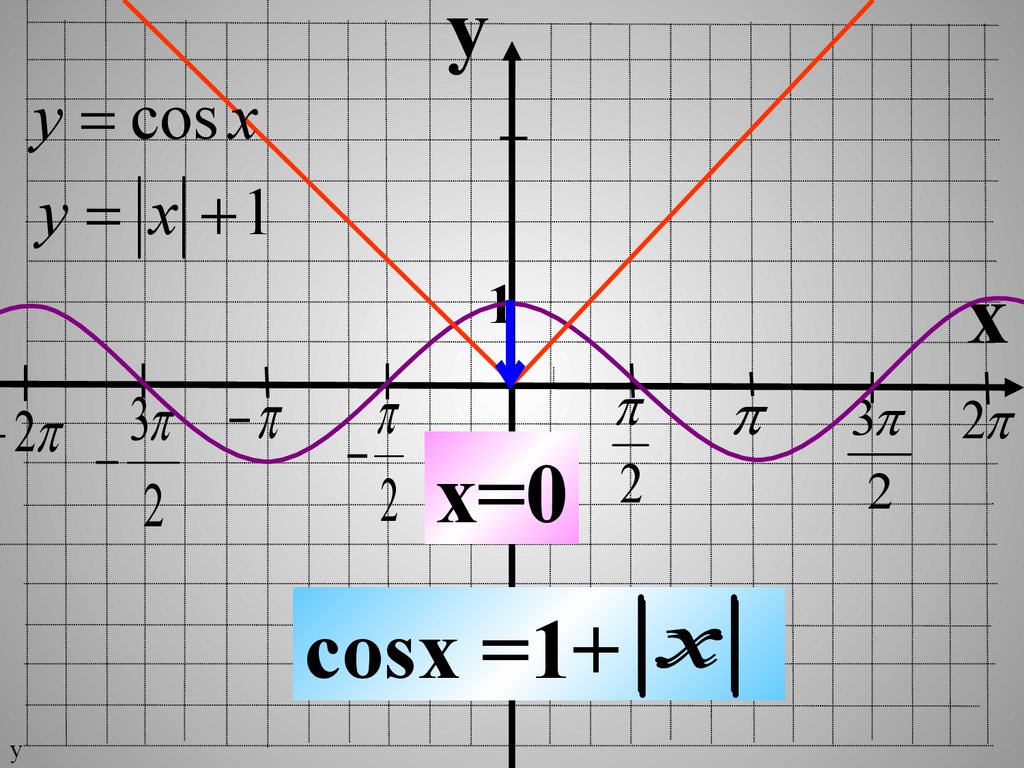
29.
y cos xy х 1
y
x
1
2 3
2
-1 2
2 x=0
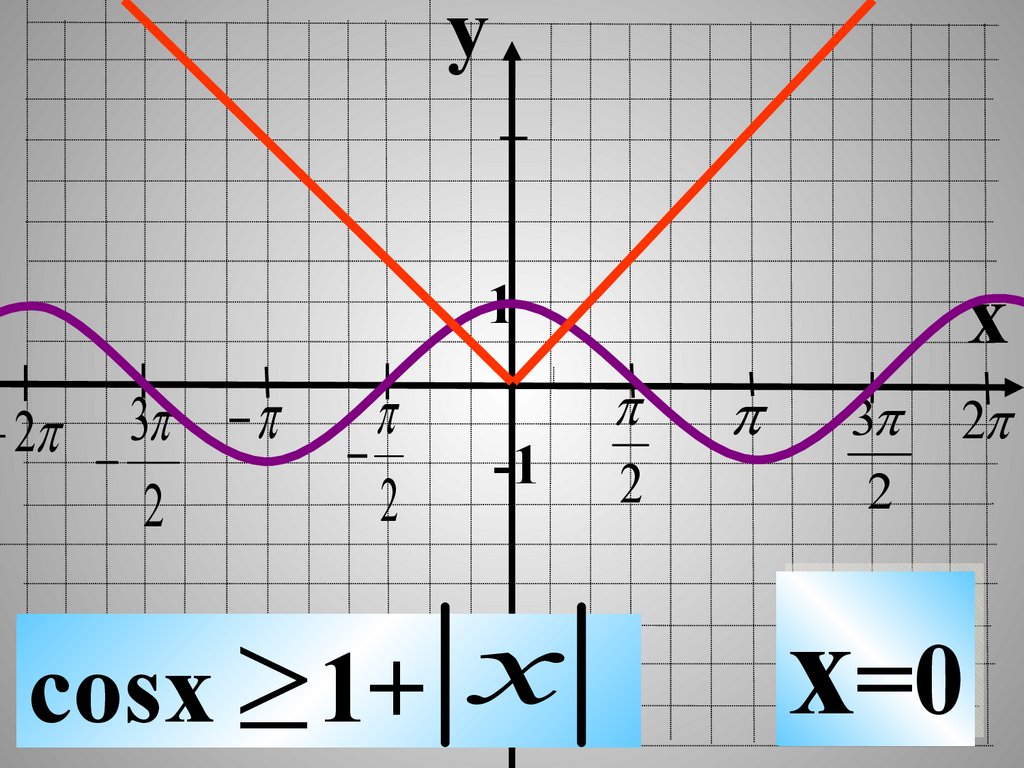
cosx =1+ x
у
3
2
2
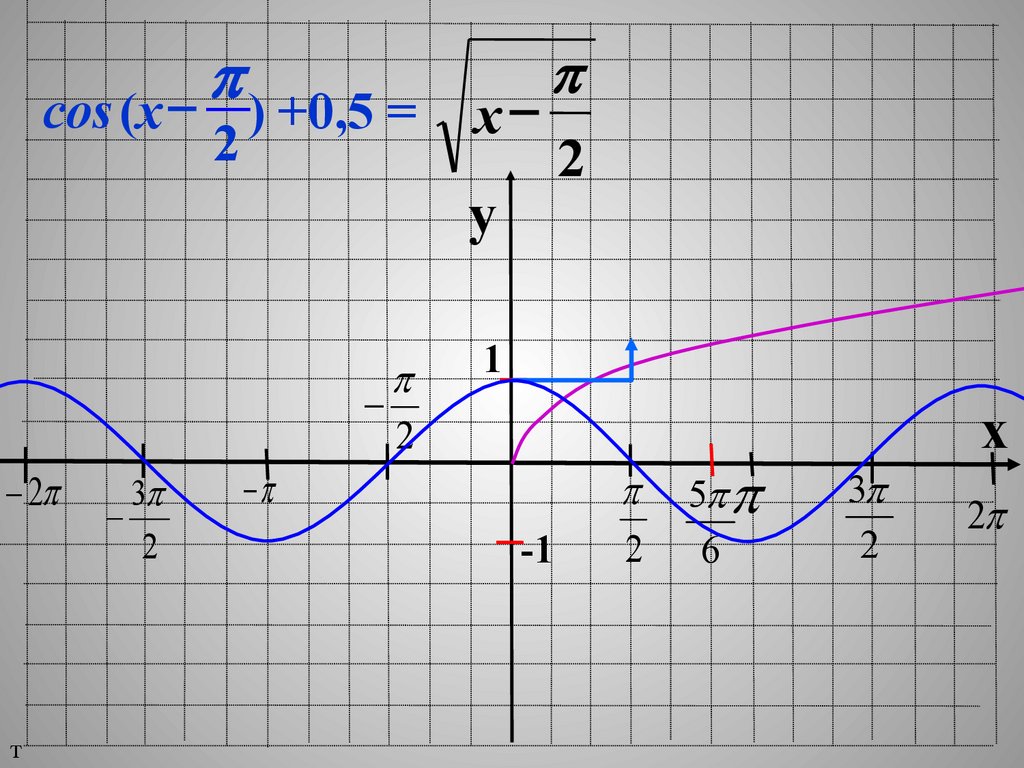
30.
pcos (x - ) +0,5 =
2
x-
p
y
2
2
т
3
2
2
1
-1
2
5
6
x
3
2
2
31.
yx
1
2 3
2
2
-1
cosx 1+ x
2
3
2
2
x=0
32.
yx
1
2 3
2
2
-1
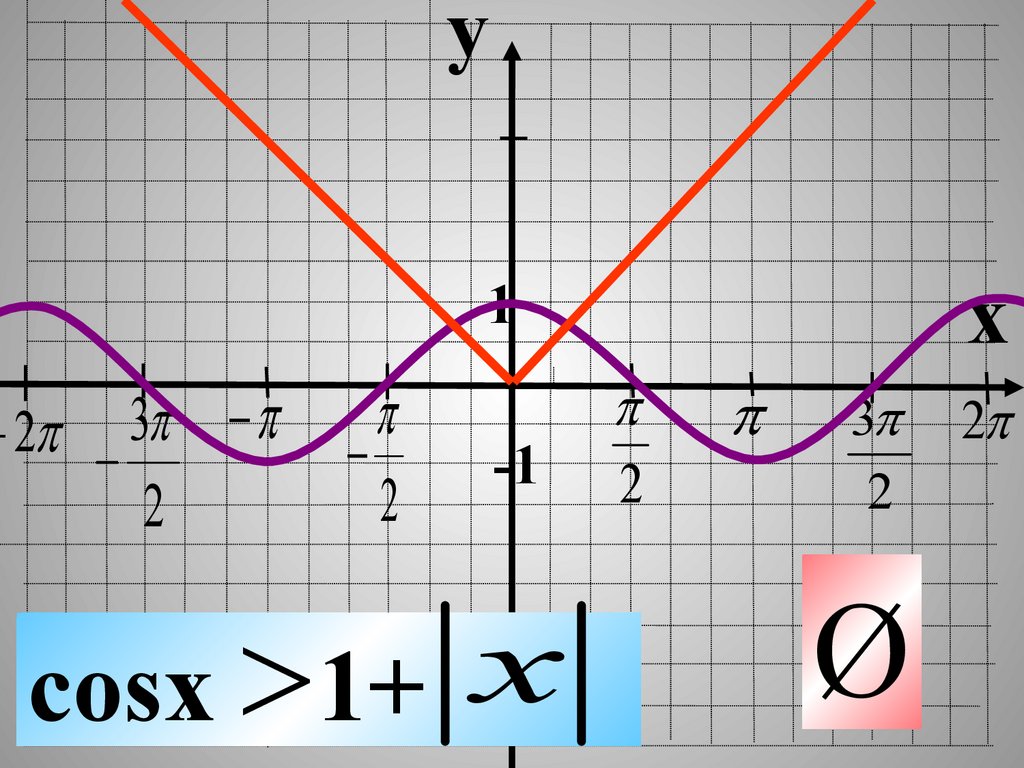
cosx 1+ x
2
3
2
Ø
2
33.
yx
1
2 3
2
2
-1
x
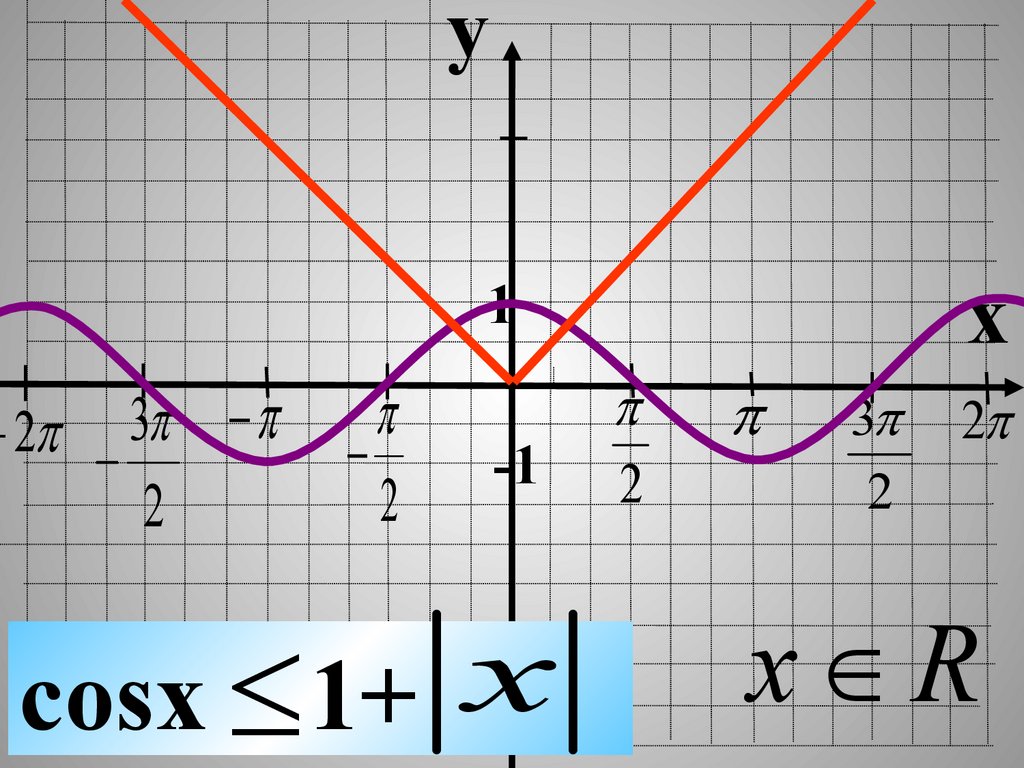
cosx 1+
2
3
2
2
x R
34.
yx
1
2 3
2
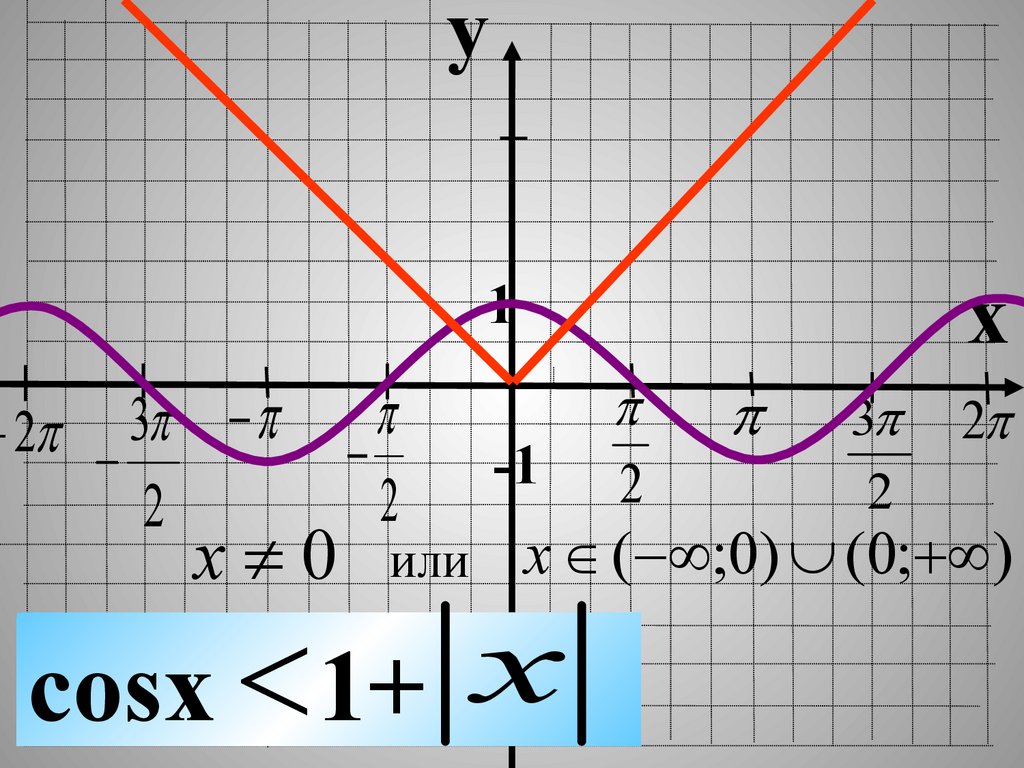
x 0
2
или
-1
2
3
2
2
x ( ;0) (0; )
cosx 1+ x
35.
Научись встречать беду не плача:Горький миг - не зрелище для всех.
Знай: душа растет при неудачах
И слабеет, если скор успех.
Мудрость обретают в трудном споре.
Предначертан путь нелегкий твой
Синусоидой радости и горя,
А не вверх взмывающей кривой.
Е. Долматовский










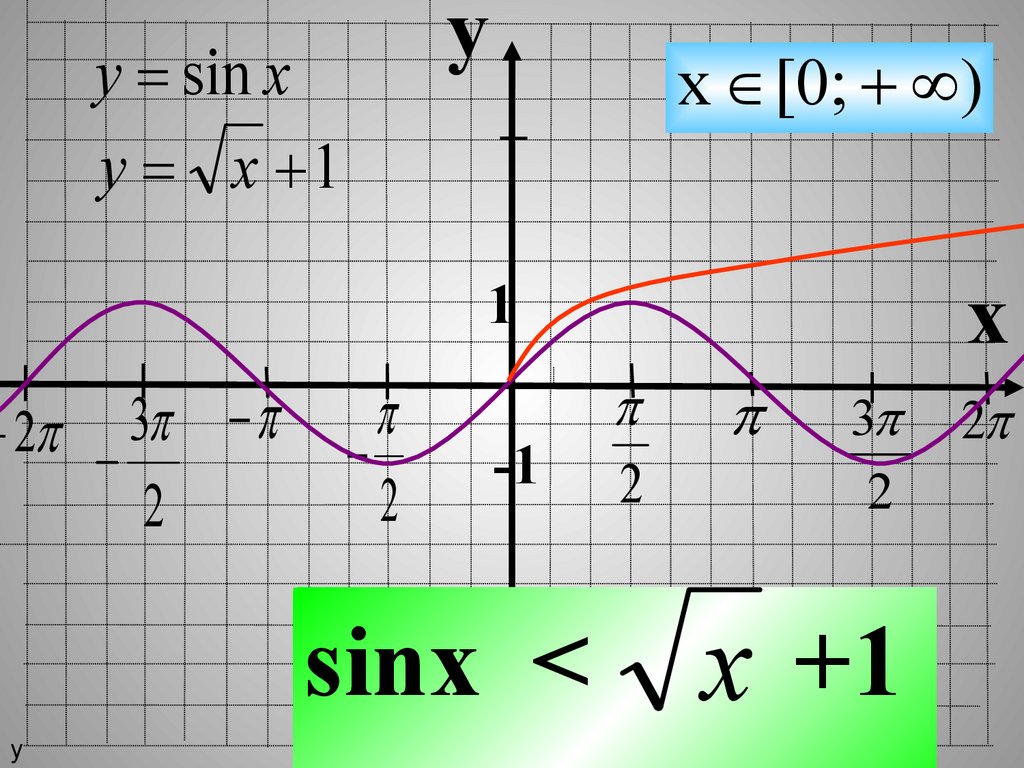

 Математика
Математика








