Teoreticheskoe-opisanie-algoritma

1.

Упорядочивание max-кучи

2.

Теоретическое описание
алгоритма
Max-куча (двоичная куча) — это структура данных типа двоичного
дерева, которая удовлетворяет свойству кучи: значение в каждом
родительском узле больше или равно значениям в его дочерних узлах.
Это означает, что максимальный элемент всегда находится в корне
дерева.
Построение max-кучи (Build Max Heap):
Исходный неотсортированный массив представляется в виде
двоичного дерева.
Сортировка (Sorting):
Извлечение максимума: Максимальный элемент (корень)
меняется местами с последним элементом кучи. Теперь
самый большой элемент находится на своей окончательной
Алгоритм проходит по всем узлам, которые являются родителями позиции.
(т.е. от индекса n/2 - 1 до 0), и для каждого из них вызывается
Уменьшение кучи: Размер кучи уменьшается на один
процедура heapify (переупорядочивание), которая "просеивает"
элемент (последний элемент теперь считается
узел вниз, чтобы восстановить свойство max-кучи.
отсортированным и исключается из рассмотрения).
Восстановление кучи: На корень дерева встал новый,
В результате этого этапа максимальный элемент оказывается в
возможно, маленький элемент. Чтобы восстановить свойство
корне дерева (в начале массива).
max-кучи, вызывается процедура heapify для нового корня.
Шаги повторяются до тех пор, пока в куче не останется один
элемент.

3.

Оценка вычислительной сложности
Алгоритм Heapsort имеет предсказуемую и стабильную производительность, что делает его надежным выбором для сортировки.
Построение кучи
Сортировка
(каждый из n вызовов heapify требует
\log n операций).
Извлечение элементов

4.

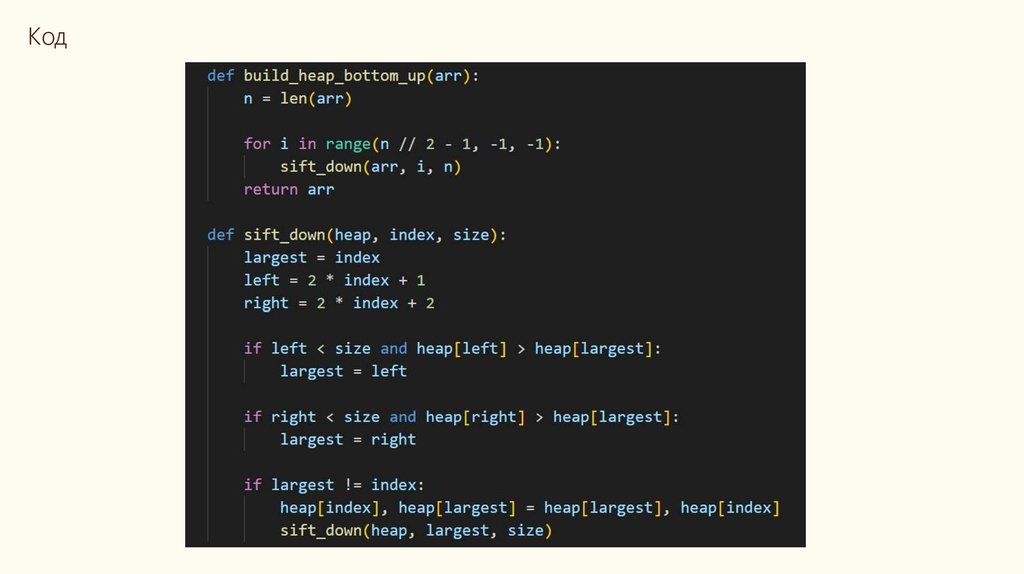
Код

5.

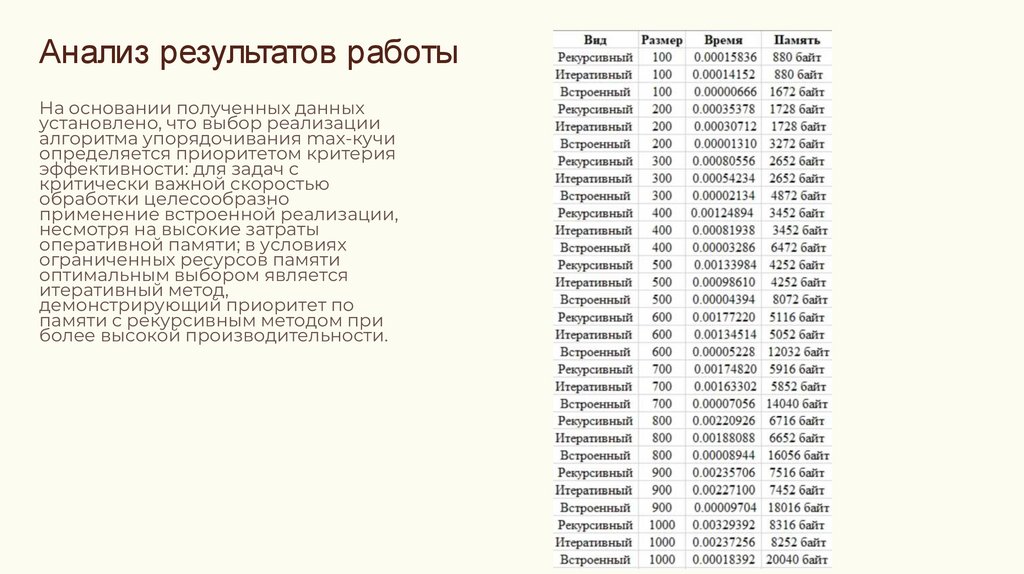
Анализ результатов работы
На основании полученных данных
установлено, что выбор реализации
алгоритма упорядочивания max-кучи
определяется приоритетом критерия
эффективности: для задач с
критически важной скоростью
обработки целесообразно
применение встроенной реализации,
несмотря на высокие затраты
оперативной памяти; в условиях
ограниченных ресурсов памяти
оптимальным выбором является
итеративный метод,
демонстрирующий приоритет по
памяти с рекурсивным методом при
более высокой производительности.

6.

Спасибо за внимание!