Похожие презентации:
Ряды динамики т6
1. Ряды динамики
РЯДЫ ДИНАМИКИ1
2.
Ряды динамики (временные ряды)применяются для изучения
изменения явлений во времени. Ряд
динамики представляет собой ряд
числовых значений определенного
статистического показателя в
последовательные моменты или
периоды времени
2
3. Ряд динамики
РЯД ДИНАМИКИэто
последовательность
изменяющихся во времени
значений
статистического
показателя , расположенного в
хронологическом порядке
3
4.
Составными элементами рядадинамики являются показатели
уровней ряда и периоды времени
(годы , кварталы , сутки) или
моменты (даты) времени. Уровни
ряда обычно обозначаются через
«y» , моменты или периоды
времени , к которым относятся
уровни – через «t»
4
5. Основные правила построения динамических рядов
Требованиясопоставимости данных
1)
2)
3)
Все показатели одного динамического ряда
должны относиться к равнозначным
периодам времени (очевидно, что данные
за год и за квартал несопоставимы);
Показатели динамического ряда должны
быть однородны по составу, т.е. иметь одну и
ту же полноту охвата объектов наблюдения;
Показатели должны быть рассчитаны по
единой методологии;
5
6.
Примерt
yi
2016
15
2017
17
2018
18,5
2019
19
9 месяцев 2020
21
Здесь t – время;
yi – производство продукции, тыс. шт.
6
7.
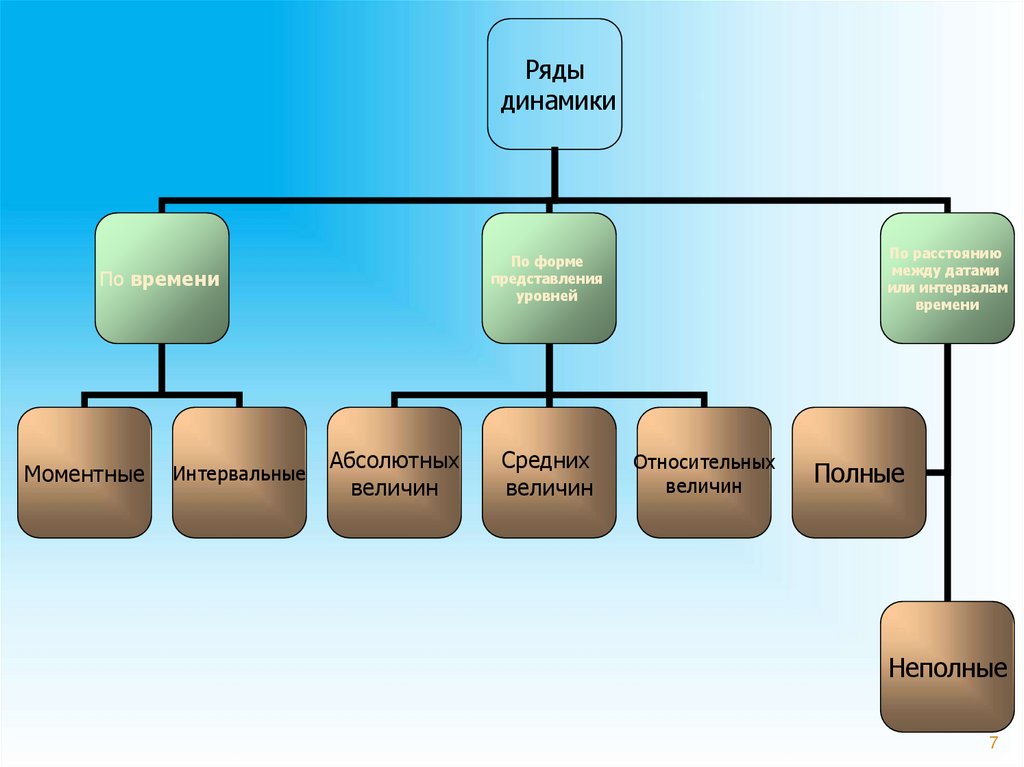
Рядыдинамики
По времени
Моментные
Интервальные
По расстоянию
между датами
или интервалам
времени
По форме
представления
уровней
Абсолютных
величин
Средних
величин
Относительных
величин
Полные
Неполные
7
8.
Ряды динамики подразделяются намоментные и интервальные.
Моментным называется ряд,
абсолютные уровни которого
характеризуют величину явления по
состоянию на определенные моменты
времени или даты. (Например,
численность населения, уровни
товарных остатков)
8
9.
Интервальным называется такой ряд,абсолютные уровни которого
представляют собой итоговые величины за
некоторые интервалы времени (например,
производство продукции за месяц; число
родившихся за месяц, год).
Особенностью интервальных рядов является то,
что их уровни можно дробить и складывать
9
10.
Выделяют также производные рядыдинамики, которые состоят из средних
или относительных величин. Они
рассчитываются на основе моментных
или интервальных рядов. (Например,
среднегодовая численность населения)
10
11.
Основные показатели,применяемые для анализа рядов
динамики
11
12.
Анализ скорости и интенсивностиявления
во
времени
осуществляется
с
помощью
статистических показателей , которые
получаются в результате сравнения
уровней между собой . Сравниваемый
уровень называют отчётным, а
уровень, с которым происходит
сравнение – базисным
12
13.
Различают показатели измененияуровней
ряда
и
средние
характеристики рядов динамики
13
14.
Кпоказателям
уровней
ряда
изменения
относятся
абсолютный
прирост,
коэффициент
роста
и
прироста, темп роста и
прироста,
абсолютное
значение 1% прироста (роста)
14
15.
1.Абсолютные приросты бываютцепными и базисными. Абсолютный
прирост показывает, на сколько
изменился изучаемый показатель по
сравнению с предыдущим или базисным
периодом времени
15
16.
Базисный абсолютныйприрост:
ΔБ Yi Y0 ,
где y 0 - базисный уровень ряда
16
17.
Цепной абсолютныйприрост:
Δц Yi Yi 1 ,
где Yi - текущий уровень ряда;
Yi 1 - предыдущий уровень
ряда
17
18.
2. Коэффициент ростапоказывает, во сколько раз изменился
изучаемый показатель по сравнению
с предыдущим периодом времени
или с базисным периодом времени.
Соответственно коэффициент роста
может быть цепным и базисным
18
19.
Цепной коэффициентроста:
ц
K Pi
y
i
yi-1
19
20.
Базисный коэффициентроста:
yi
K
y0
б
Pi
20
21.
3.Темпы роста – этокоэффициенты роста, выраженные в
процентах (они также могут быть
цепными, базисными и средними):
Tр= Kp • 100 (%)
21
22.
Темп роста:а) базисный:
/
*
100
y
y
Tp
i
0
б) цепной :
/
100
y
y
Tp
i
i 1
22
23.
4.Темп прироста используется длявыражения
величины
абсолютного
прироста уровней ряда динамики в
относительных величинах:
100
T np T p
23
24.
Темп прироста показывает, насколько процентов изменился
изучаемый показатель по сравнению
с предыдущим периодом времени
или с базисным периодом времени.
Цепной темп прироста:
Yi Yi 1
ц
ц
Т прi
100 Т pi 100
yi-1
24
25.
Базисный темп приростаТ
б
ПРi
Yi Y 0
б
100 Т pt 100
y0
25
26.
5. Абсолютное значение одногопроцента прироста А% показывает,
сколько абсолютных единиц
содержится в 1% прироста
26
27.
Содержание одного процентабазисного прироста:
Δ
yt y 0
y0
А%
yt y 0
T
100
100
y0
б
t
б
t
б
прt
15
0,15
100
27
28.
Содержание одного процентацепного прироста:
Δ
yt yt 1
yt 1
А%
yt yt 1
T
100
100
yt 1
ц
t
ц
t
ц
прt
28
29.
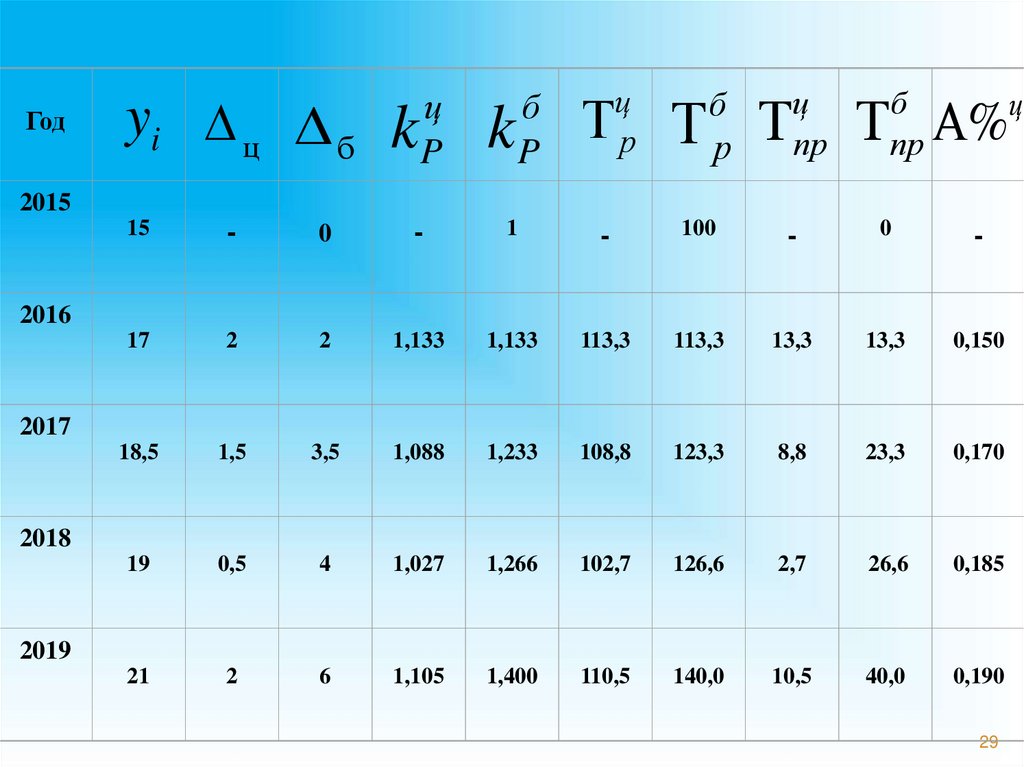
Годyi D ц Δ б k
ц
P
k
б
P
ц
р
б
р
ц
пр
%
б
пр
2015
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2016
2017
2018
2019
29
ц
30.
Расчет среднего уровня рядадинамики
30
31. средние характеристики ряда
СРЕДНИЕ ХАРАКТЕРИСТИКИ РЯДАСредний
уровень
ряда
динамики
рассчитывается
по
формулам
средней
арифметической
или
средней
хронологической
31
32.
1.Еслиряд
динамики
является
интервальным, то расчет среднего
уровня ведется по формуле простой
средней арифметической:
Y
Y
i
n
32
33. Средний уровень ряда
СРЕДНИЙ УРОВЕНЬ РЯДАДЛЯ ИНТЕРВАЛЬНЫХ РЯДОВ
С РАВНЫМИ ИНТЕРВАЛАМИ ВРЕМЕНИ
Простая средняя арифметическая
y
/
n
y
=
i
где n - количество периодов времени
33
34.
Пример. Имеются следующие данные о динамикепроизводства продукции предприятием за 20152019 гг., тыс. шт.
2015 г.
2016 г.
2017 г.
2018 г.
2019 г.
205
213
222
229
236
Определить
среднегодовое
продукции за 2015-2019 гг.
производство
205 213 222 229 236 1105
Y
221 тыс. шт.
5
5
34
35.
2. Если ряд динамики является моментным сразличными интервалами времени между датами, то
для расчета среднего уровня используется средняя
арифметическая взвешенная:
t
где i – продолжительность i-го интервала времени
(интервал времени между двумя соседними
значениями;
Yi - средний уровень ряда для i-го интервала
времени
35
36.
С неравными интервалами времениЭта формула иногда дается как взвешенная средняя
хронологическая
y
=
y y t / 2 t
i
i 1
i
i
где ti – период времени между двумя
соседними значениями
36
37.
Пример. Известна списочная численностьперсонала организации по состоянию на
следующие даты (человек) :
01.01
01.03
01.06
01.09
01.01
след.год
1200
1100
1250
1500
1350
Среднесписочная численность персонала за
год составляет:
1200 1100
1100 1250
1250 1500
1500 1350
2
3
3
4
2
2
2
2
у
12
31300
1304 чел.
24
37
38.
3.Если ряд динамики является моментным сравноотстоящими уровнями, то используется
средняя хронологическая простая:
y1
yn
y 2 y3 ... y n-1
2 ,
y 2
n 1
где n-количество дат
38
39.
Пример. Известны товарные остаткимагазина на 1-е число каждого месяца
(тыс. руб.) :
01.01
01.02
01.03
01.04
180
140
160
200
Средний уровень товарных остатков за
первый квартал составил:
180
200
140 160
2 163тыс. руб.
у 2
3
39
40.
Средний абсолютный приростопределяется как простая средняя
арифметическая величина из цепных
абсолютных приростов и показывает,
на сколько в среднем изменялся
показатель в течение изучаемого
периода времени
40
41.
Средний абсолютный приростпоказывает, на сколько в среднем изменялся
изучаемый показатель при переходе от
предыдущего периода времени к смежному
последующему периоду времени
ΣΔi Σ(Yi Yi 1 ) Yn Y 1
Δ
,
s
s
n 1
где
n – число уровней ряда динамики;
S = n - 1 – количество цепных приростов
41
42.
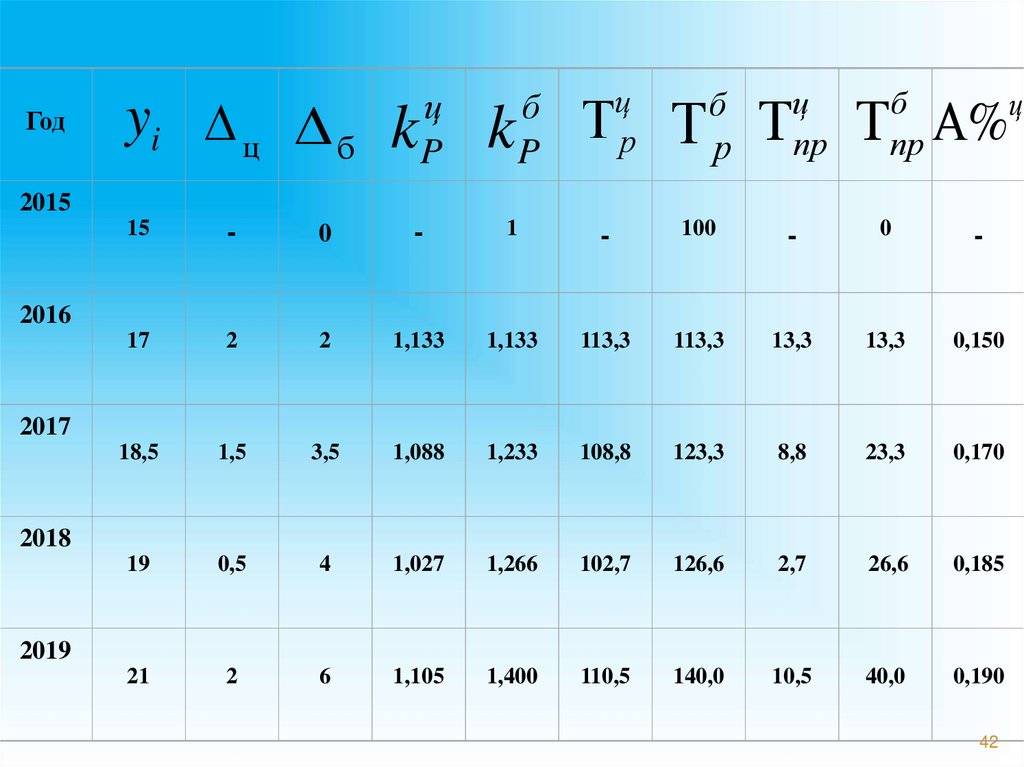
Годyi D ц Δ б k
ц
P
k
б
P
ц
р
б
р
ц
пр
%
б
пр
2015
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2016
2017
2018
2019
42
ц
43.
2 1,5 0,5 2Δ
1,5
5 1
21 15
Δ
1,5
5 1
43
44.
Среднегодовойкоэффициент
роста определяется как средняя
геометрическая
из
цепных
коэффициентов роста и показывает ,
сколько в среднем составлял рост
показателя
44
45.
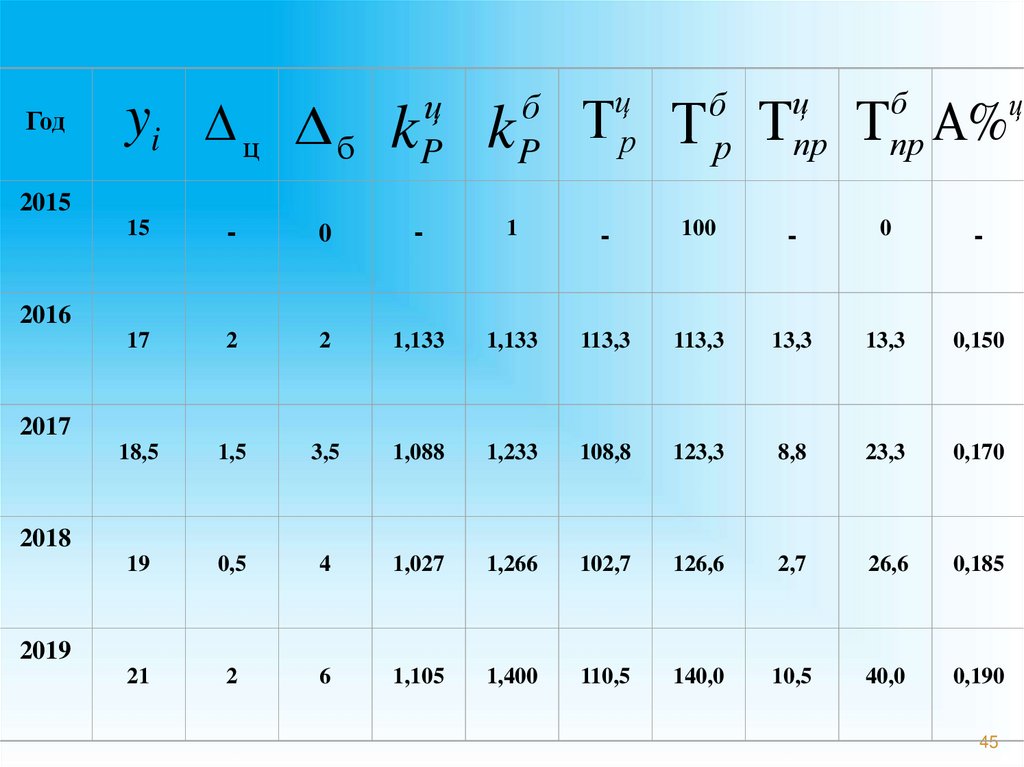
Годyi D ц Δ б k
ц
P
k
б
P
ц
р
б
р
ц
пр
%
б
пр
2015
15
-
0
-
1
-
100
-
0
-
17
2
2
1,133
1,133
113,3
113,3
13,3
13,3
0,150
18,5
1,5
3,5
1,088
1,233
108,8
123,3
8,8
23,3
0,170
19
0,5
4
1,027
1,266
102,7
126,6
2,7
26,6
0,185
21
2
6
1,105
1,400
110,5
140,0
10,5
40,0
0,190
2016
2017
2018
2019
45
ц
46.
Средний коэффициент ростарассчитывается по формуле средней
геометрической из цепных
коэффициентов роста:
k
n 1
ц
ц
ц
ц
2
3
4
n
k k k ... k
k 5 1 1,133 1,088 1,027 1,105 1,088
46
47.
yn21
k n 1
4
1,088
y1
15
47
48.
Среднегодовойтемп
роста
определяется
умножением
среднегодового коэффициента роста
на 100 и показывает , сколько
процентов в среднем составлял рост
показателя
48
49. Средний темп прироста
СРЕДНИЙ ТЕМП ПРИРОСТАПоказывает, на сколько процентов
увеличивается (или уменьшается)
уровень по сравнению с предыдущем в
среднем за единицу времени:
Т пр Т р 100
49
50.
Т пр 108,8% 100% 8,8%50
51.
Проблема сопоставимостиуровней рядов динамики
Смыкание рядов динамики
51
52.
Поскольку ряды динамикиформируются на протяжении
длительных периодов времени, их
уровни часто оказываются
несопоставимыми
52
53.
Причины1. Изменение цен
2. Изменение методики расчета
показателей
Изменение «границ» (организационных,
административных)
53
54.
Для обеспечения сопоставимости данныхчасто применяется метод смыкания рядов
динамики. Для смыкания ряда динамики
необходимо иметь переходное звено.
(Переходное звено – это период времени,
для которого изучаемый показатель
рассчитан как по старой методике (в старых
границах), так и по новой методике (в новых
границах).
Для переходного звена рассчитывается
коэффициент, действие которого
распространяется на все предшествующие
периоды времени
54
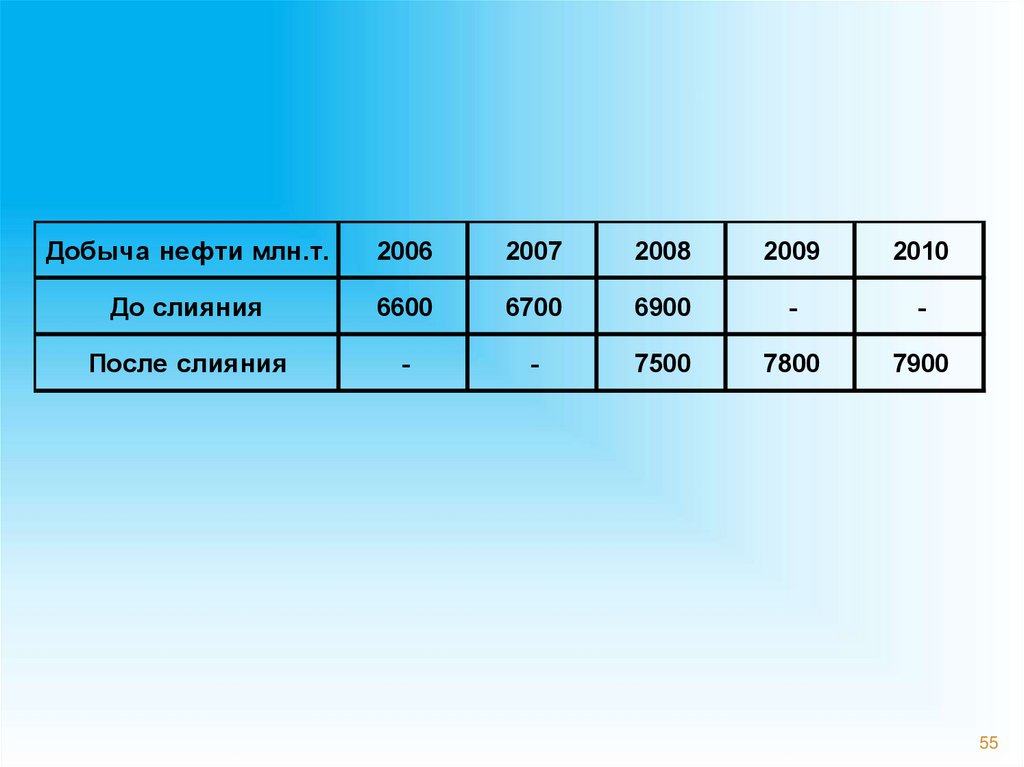
55.
Добыча нефти млн.т.2006
2007
2008
2009
2010
До слияния
6600
6700
6900
-
-
После слияния
-
-
7500
7800
7900
55
56.
7500К
1,087
6900
56
57.
y07 6700 1,087 7283y06 6600 1,087 7174
57
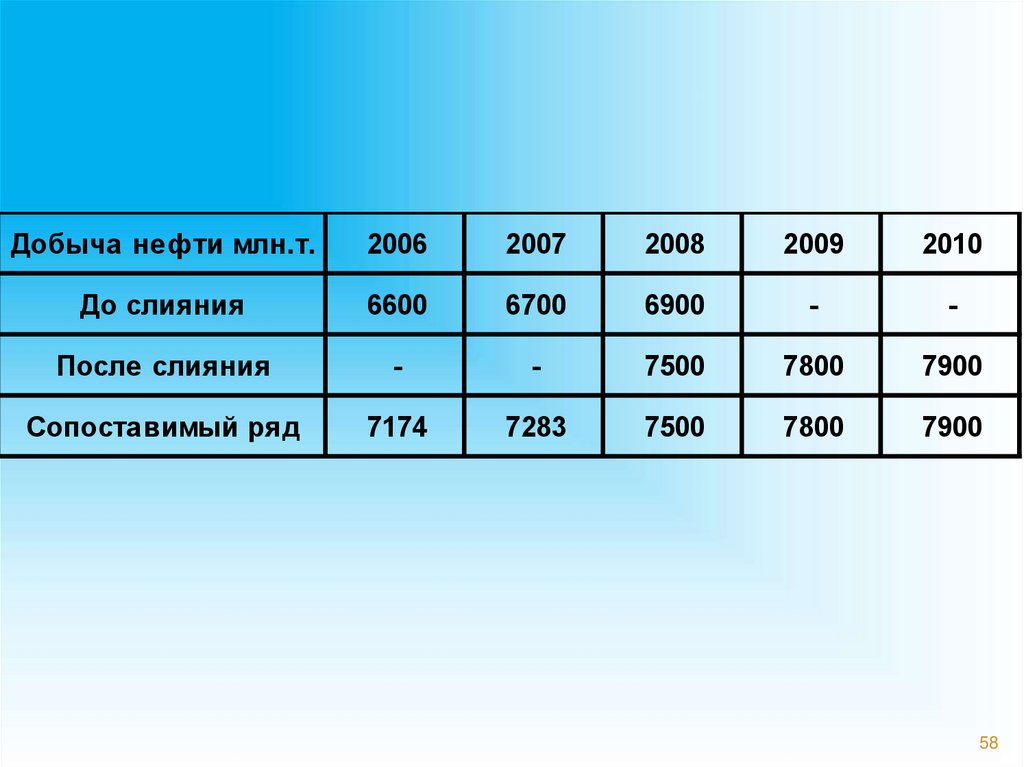
58.
Добыча нефти млн.т.2006
2007
2008
2009
2010
До слияния
6600
6700
6900
-
-
После слияния
-
-
7500
7800
7900
Сопоставимый ряд
7174
7283
7500
7800
7900
58
59.
Анализ основной тенденциирядов динамики
59
60.
Уровни рядов динамикиформируются под воздействием
большого числа факторов. Их
можно разделить на 3 группы
60
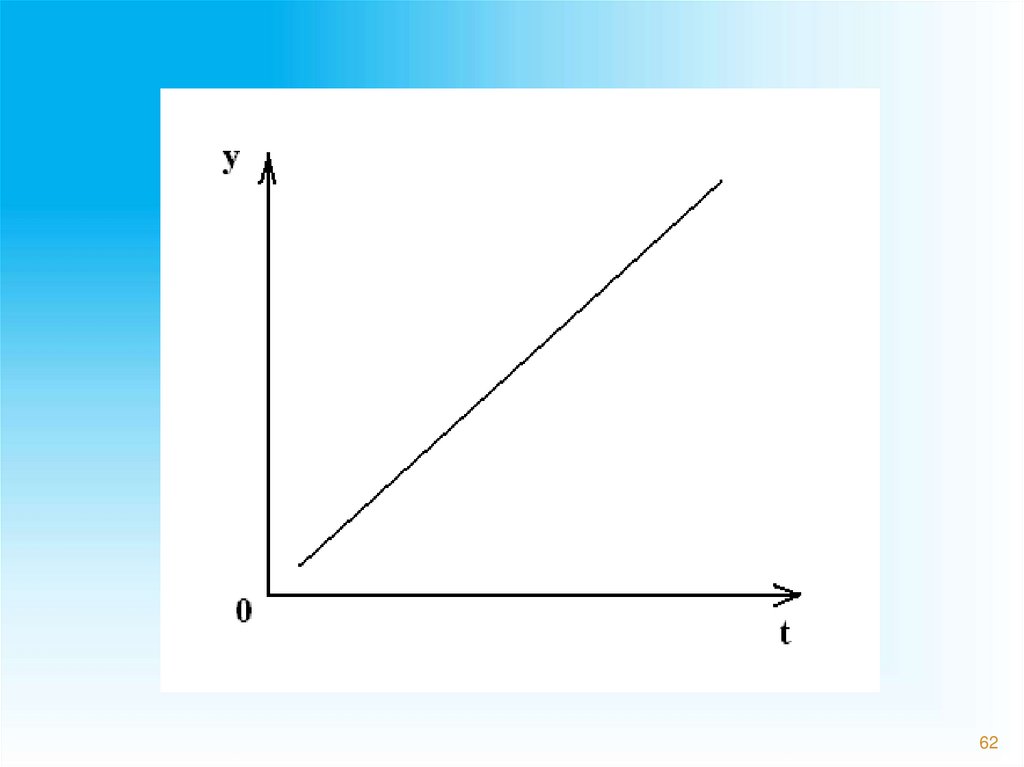
61.
1. Определяющие факторы –факторы, которые оказывают
постоянное и сильное воздействие на
изучаемый показатель. Они
определяют основную тенденцию
(тренд) ряда динамики
61
62.
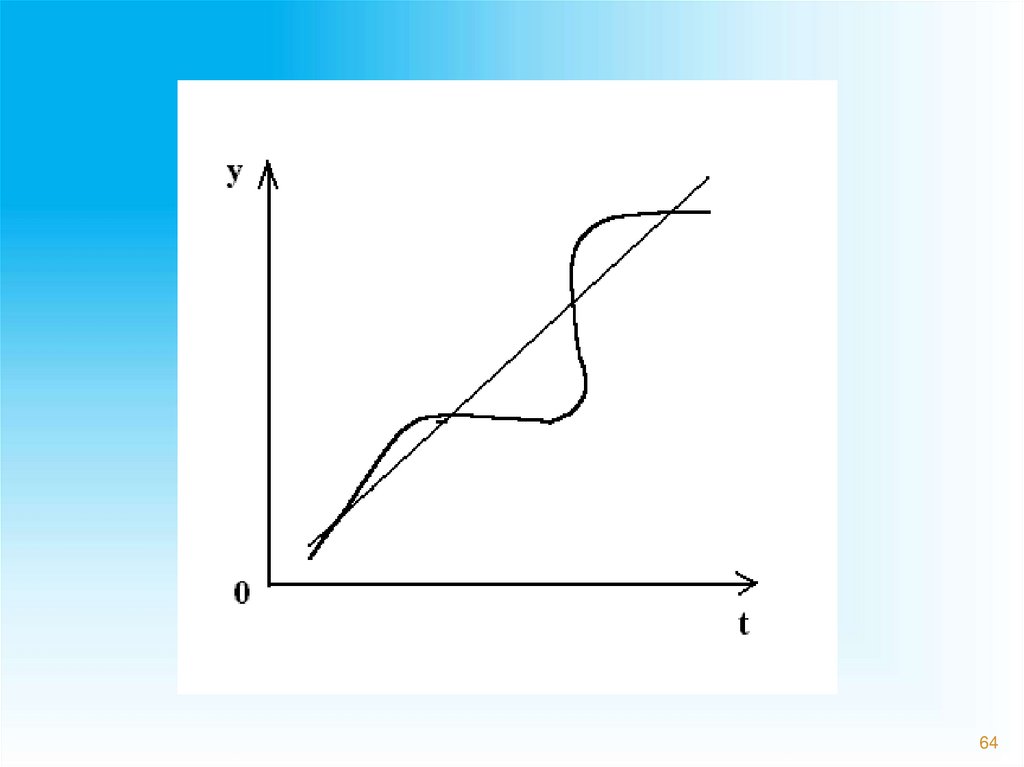
6263.
2. Сезонные факторы – факторы,которые вызывают сезонные
колебания относительно основной
тенденции
63
64.
6465.
3. Случайные факторы – факторы,которые вызывают случайные
колебания уровней ряда (например,
погодный фактор)
65
66.
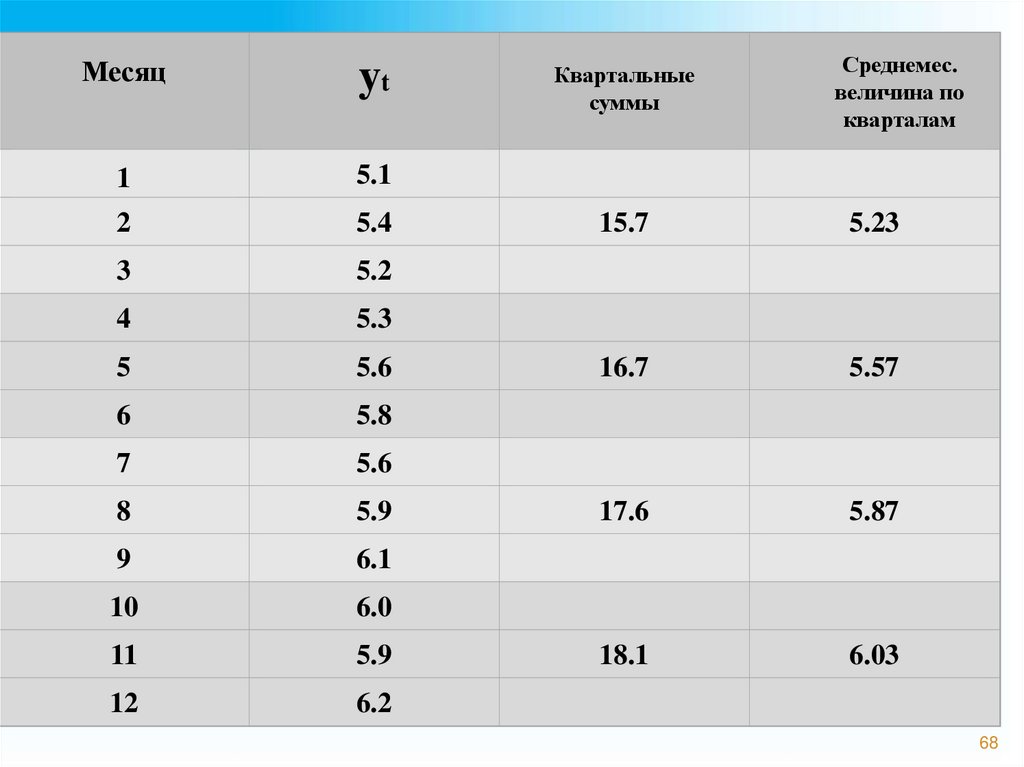
Метод укрупненияинтервалов
66
67.
Метод укрупненияинтервалов – замена исходных
уровней ряда средними
величинами, которые
рассчитываются для
укрупненных интервалов
67
68.
Месяцyt
1
5.1
2
5.4
3
5.2
4
5.3
5
5.6
6
5.8
7
5.6
8
5.9
9
6.1
10
6.0
11
5.9
12
6.2
Квартальные
суммы
Среднемес.
величина по
кварталам
15.7
5.23
16.7
5.57
17.6
5.87
18.1
6.03
68
69.
Метод скользящейсредней
69
70.
Метод скользящейсредней– замена исходных
уровней ряда средними
величинами, которые
рассчитываются для
последовательно смещающихся
интервалов времени
70
71.
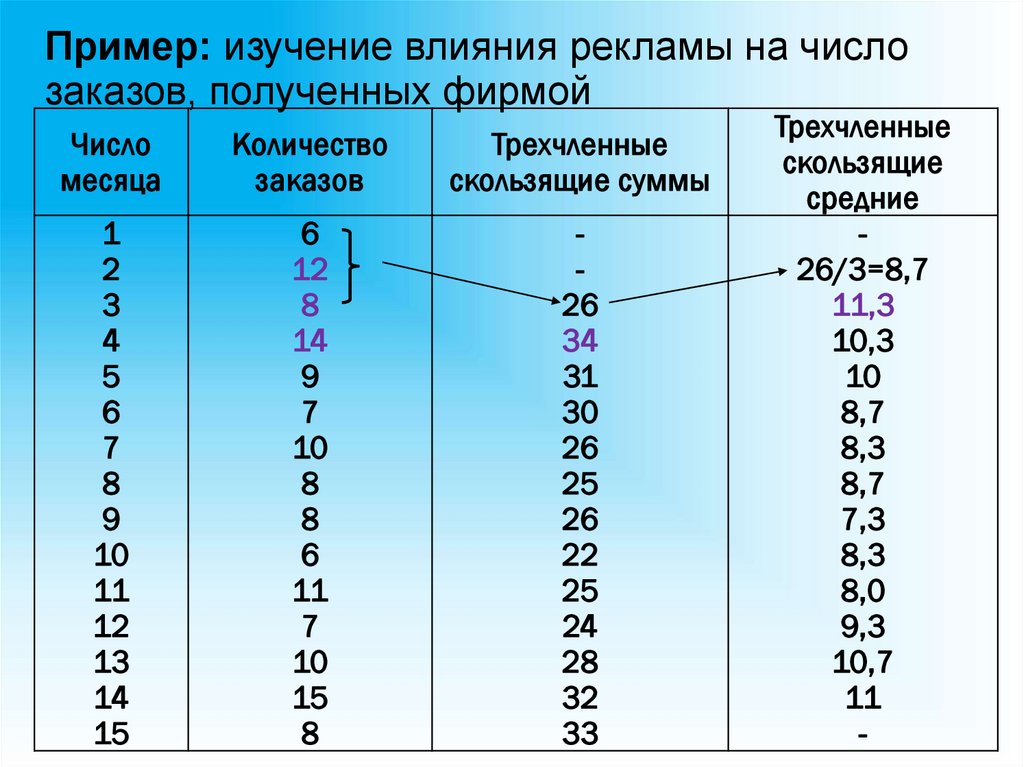
Пример: изучение влияния рекламы на числозаказов, полученных фирмой
Число
месяца
Количество
заказов
Трехчленные
скользящие суммы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6
12
8
14
9
7
10
8
8
6
11
7
10
15
8
26
34
31
30
26
25
26
22
25
24
28
32
33
Трехчленные
скользящие
средние
26/3=8,7
11,3
10,3
10
8,7
8,3
8,7
7,3
8,3
8,0
9,3
10,7
11
-
72.
1614
12
10
8
6
4
2
0
0
5
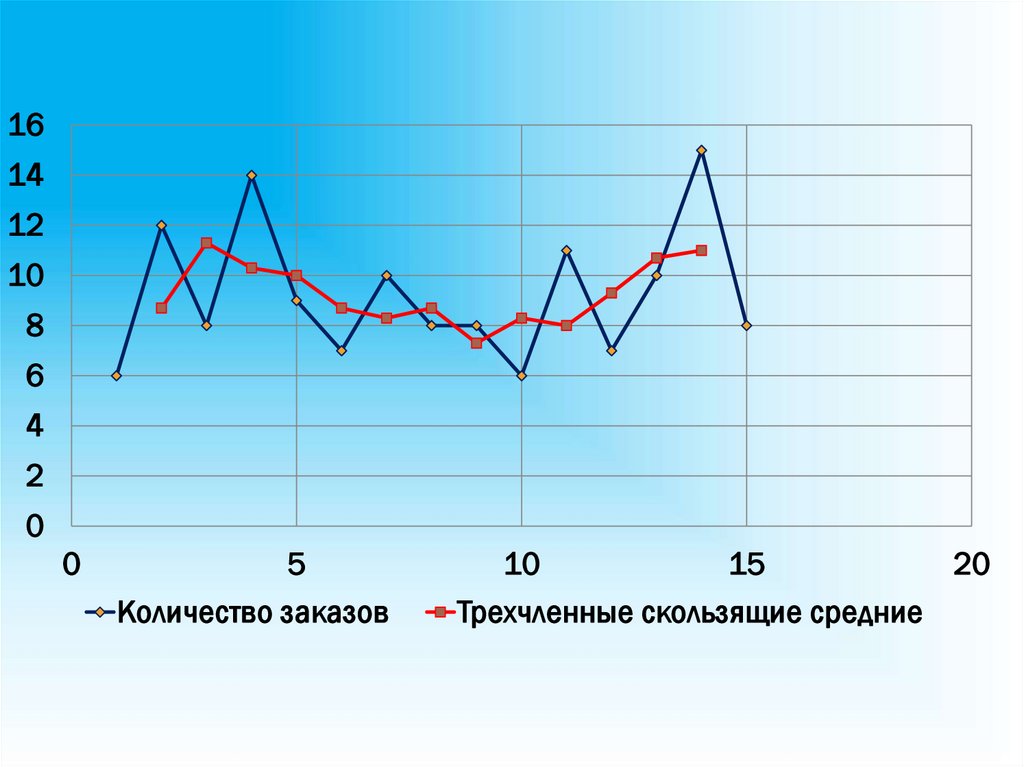
Количество заказов
10
15
Трехчленные скользящие средние
20
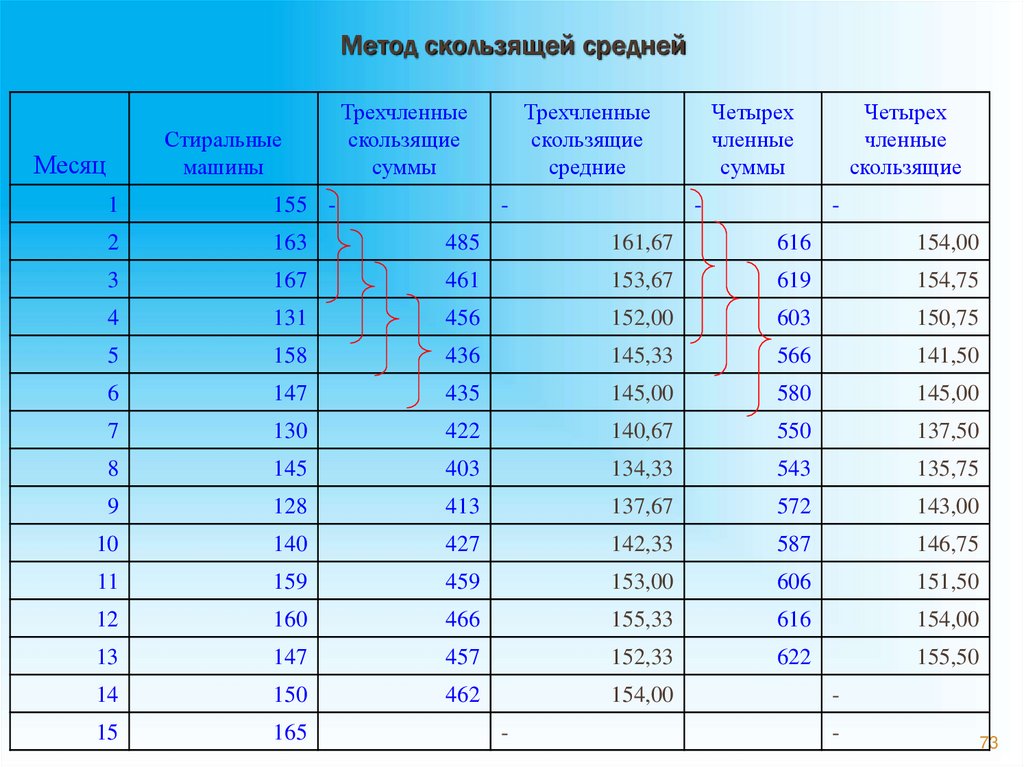
73. Метод скользящей средней
Стиральныемашины
Месяц
Трехчленные
скользящие
суммы
Трехчленные
скользящие
средние
-
Четырех
членные
суммы
1
155 -
2
163
485
161,67
616
154,00
3
167
461
153,67
619
154,75
4
131
456
152,00
603
150,75
5
158
436
145,33
566
141,50
6
147
435
145,00
580
145,00
7
130
422
140,67
550
137,50
8
145
403
134,33
543
135,75
9
128
413
137,67
572
143,00
10
140
427
142,33
587
146,75
11
159
459
153,00
606
151,50
12
160
466
155,33
616
154,00
13
147
457
152,33
622
155,50
14
150
462
154,00
15
165
-
-
Четырех
членные
скользящие
-
-
73
74.
Средняяиз нечетного числа уровней относится к
середине интервала
Если интервал сглаживания четный, то отнесение
средней к определенному времени невозможно, она
относится к середине между датами
Поэтому применяют центрирование – нахождение
средней из двух смежных скользящих средних,
которую относят уже к определенной дате
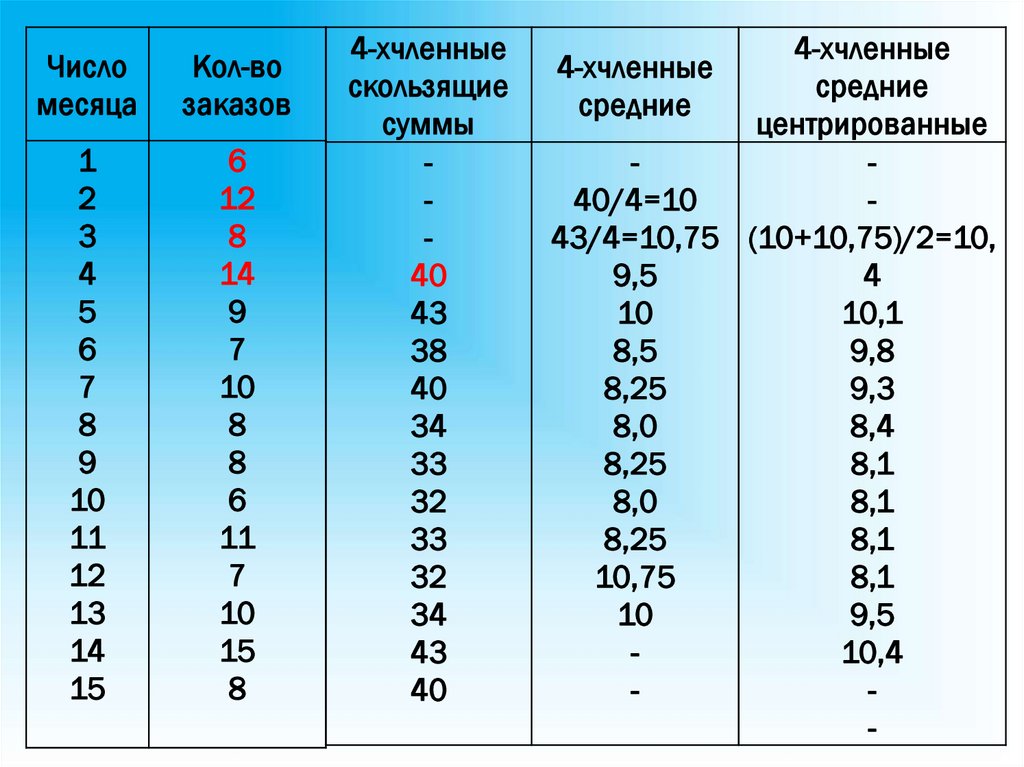
75.
Числомесяца
Кол-во
заказов
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6
12
8
14
9
7
10
8
8
6
11
7
10
15
8
4-хчленные
скользящие
суммы
40
43
38
40
34
33
32
33
32
34
43
40
4-хчленные
средние
центрированные
40/4=10
43/4=10,75 (10+10,75)/2=10,
9,5
4
10
10,1
8,5
9,8
8,25
9,3
8,0
8,4
8,25
8,1
8,0
8,1
8,25
8,1
10,75
8,1
10
9,5
10,4
4-хчленные
средние
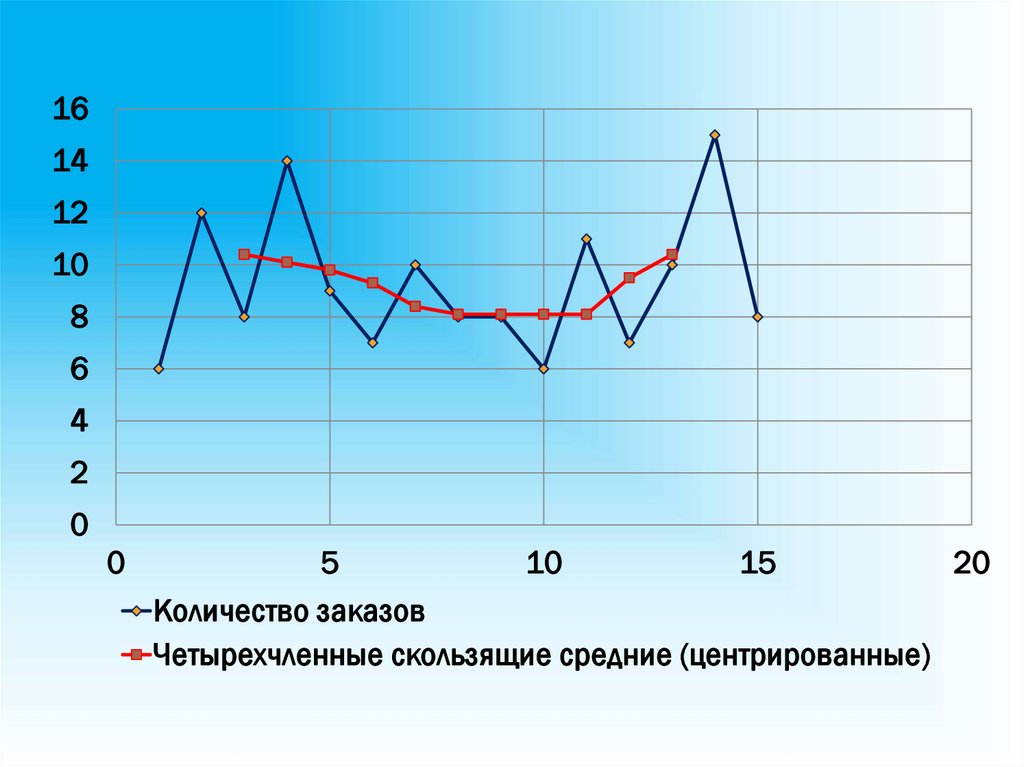
76.
1614
12
10
8
6
4
2
0
0
5
10
15
Количество заказов
Четырехчленные скользящие средние (центрированные)
20
77.
Недостаток метода простой скользящей средней:сглаженный ряд динамики сокращается, т.к.
невозможно получить сглаженные уровни для его
начала и конца
78.
Аналитическоевыравнивание рядов
динамики
78
79.
Уровни ряда рассматриваютсякак некоторая функция от
времени:
y t f(t)
79
80. Аналитическое выравнивание
линейная f (t) = a 0 a 1t ;2
па р аболи Ч еская f ( t ) a 0 a 1t a 2t ,
экспоненциальные f (t) = exp(a 0 + a 1t)
2
или f (t) = exp(a 0 + a 1t + a 2t ).
80
81. Аналитическое выравнивание
Линейная зависимость - в исходном временном ряду наблюдаютсяболее или менее постоянные абсолютные цепные приросты, не
проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость - абсолютные цепные приросты
обнаруживают некоторую тенденцию развития, но абсолютные
цепные приросты абсолютных цепных приростов (разности второго
порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости - в исходном временном ряду
наблюдается либо более или менее постоянный относительный рост
(устойчивость цепных темпов роста, темпов прироста, коэффициентов
роста), либо, при отсутствии такого постоянства, - устойчивость в
изменении показателей относительного роста (цепных темпов роста
цепных же темпов роста, цепных коэффициентов роста цепных же
коэффициентов или темпов роста и т. п.).
81
82.
Процедура выравнивания в этомслучае сводится:
к выбору вида функции;
к определению параметров функции;
к получению выравненных значений
уровней ряда на
основе функции
82
83.
Рассмотрим данный метод напримере линейного уравнения
(тренда):
Λ
y t a b t,
где a и b – параметры;
t – время
83
84.
Суть метода наименьших квадратов: выбрать такиепараметры а0, а1, ...аn, при которых сумма квадратов
отклонений расчетных значений уровней ряда от
фактических значений была бы минимальной:
85.
Линейный тренд лучше всегоиспользовать в тех случаях, когда
предварительный анализ показывает,
что уровни ряда изменяются с
примерно одинаковой скоростью, т.е.
когда цепные абсолютные приросты
примерно равны между собой
85
86.
Параметры a и b определяютсяпри помощи метода наименьших
квадратов (МНК)
86
87.
Применение метода МНК даетследующую систему уравнений для
определения параметров:
a t b t (y t t)
2
a n b t yt
87
88.
Данную систему уравненийможно существенно упростить,
если пронумеровать время таким
образом, чтобы
t 0
88
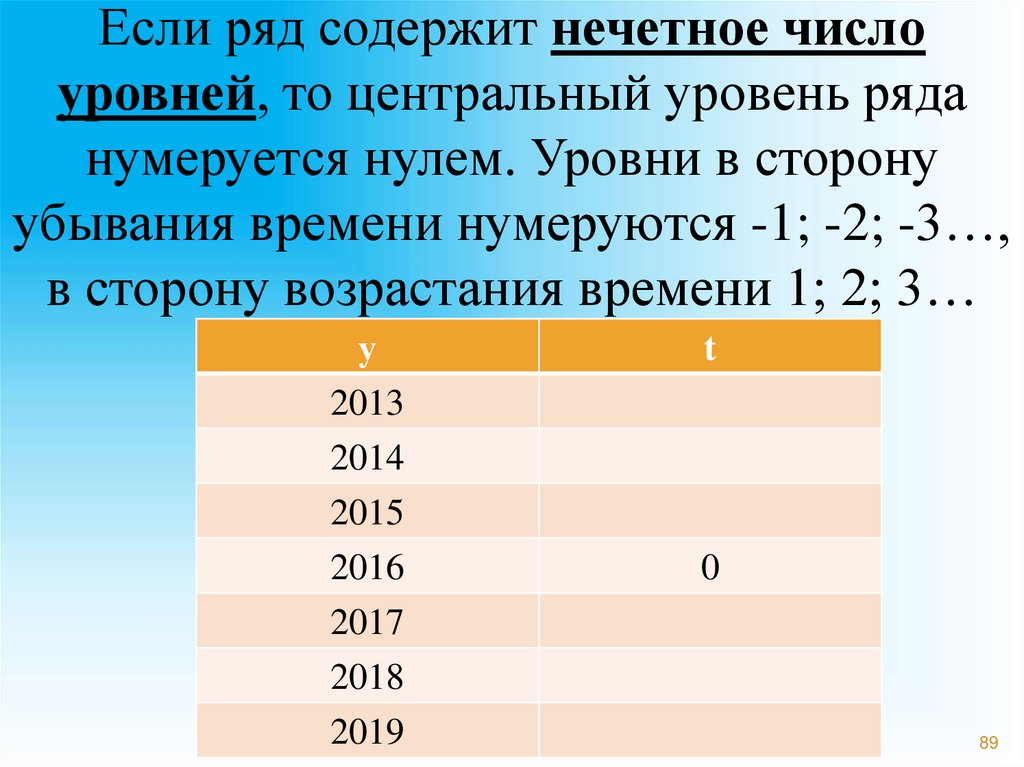
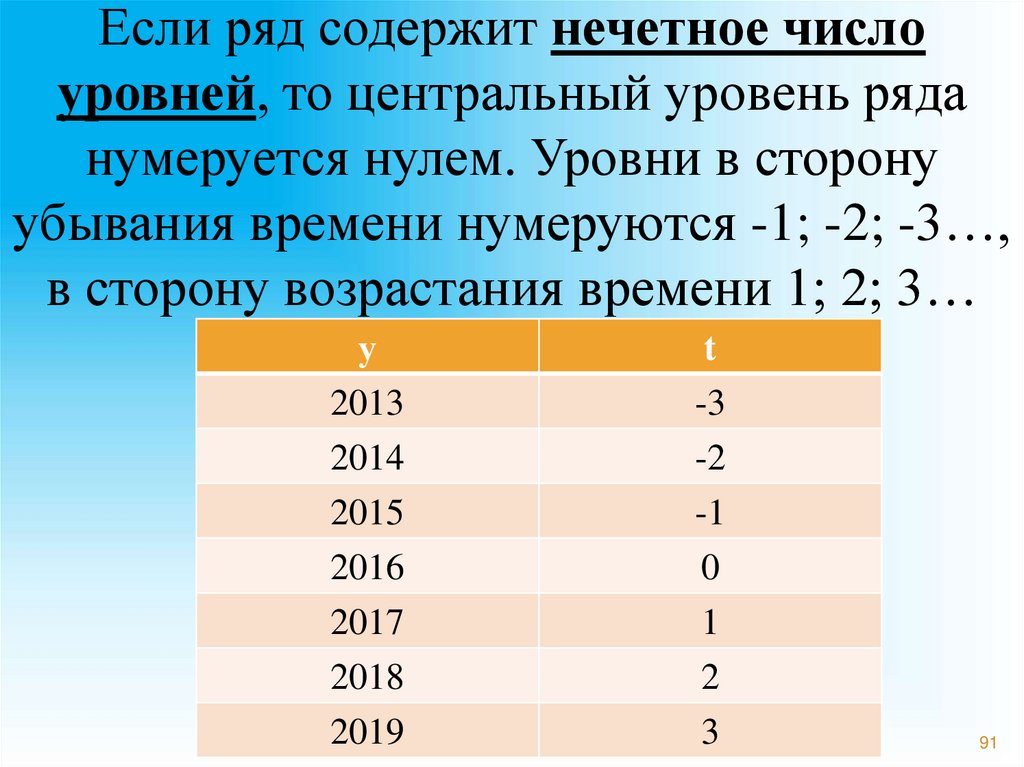
89.
Если ряд содержит нечетное числоуровней, то центральный уровень ряда
нумеруется нулем. Уровни в сторону
убывания времени нумеруются -1; -2; -3…,
в сторону возрастания времени 1; 2; 3…
у
2013
2014
2015
2016
2017
2018
2019
t
0
89
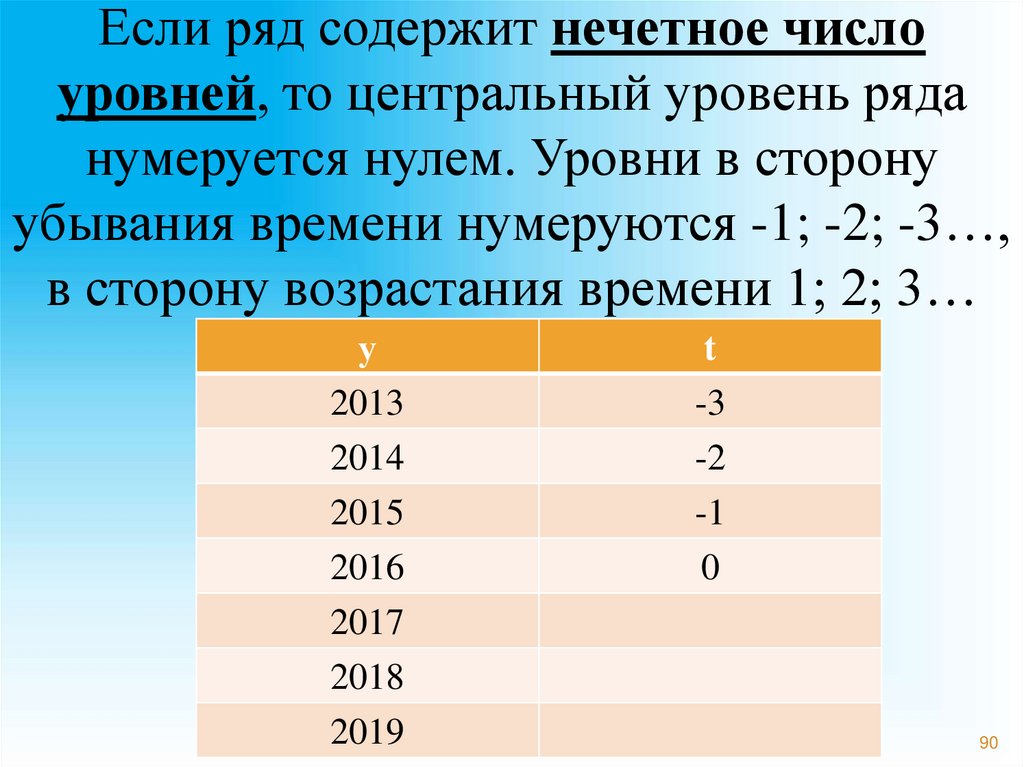
90.
Если ряд содержит нечетное числоуровней, то центральный уровень ряда
нумеруется нулем. Уровни в сторону
убывания времени нумеруются -1; -2; -3…,
в сторону возрастания времени 1; 2; 3…
у
2013
2014
2015
2016
2017
2018
2019
t
-3
-2
-1
0
90
91.
Если ряд содержит нечетное числоуровней, то центральный уровень ряда
нумеруется нулем. Уровни в сторону
убывания времени нумеруются -1; -2; -3…,
в сторону возрастания времени 1; 2; 3…
у
2013
2014
2015
2016
2017
2018
2019
t
-3
-2
-1
0
1
2
3
91
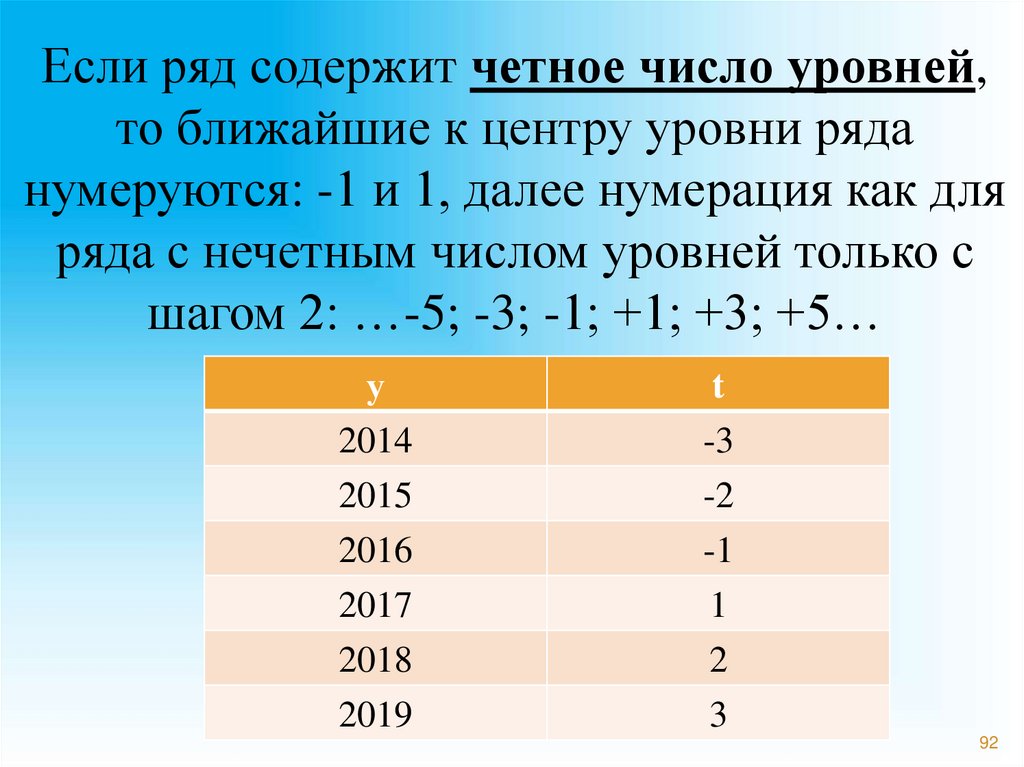
92.
Если ряд содержит четное число уровней,то ближайшие к центру уровни ряда
нумеруются: -1 и 1, далее нумерация как для
ряда с нечетным числом уровней только с
шагом 2: …-5; -3; -1; +1; +3; +5…
у
2014
2015
2016
2017
2018
2019
t
-3
-2
-1
1
2
3
92
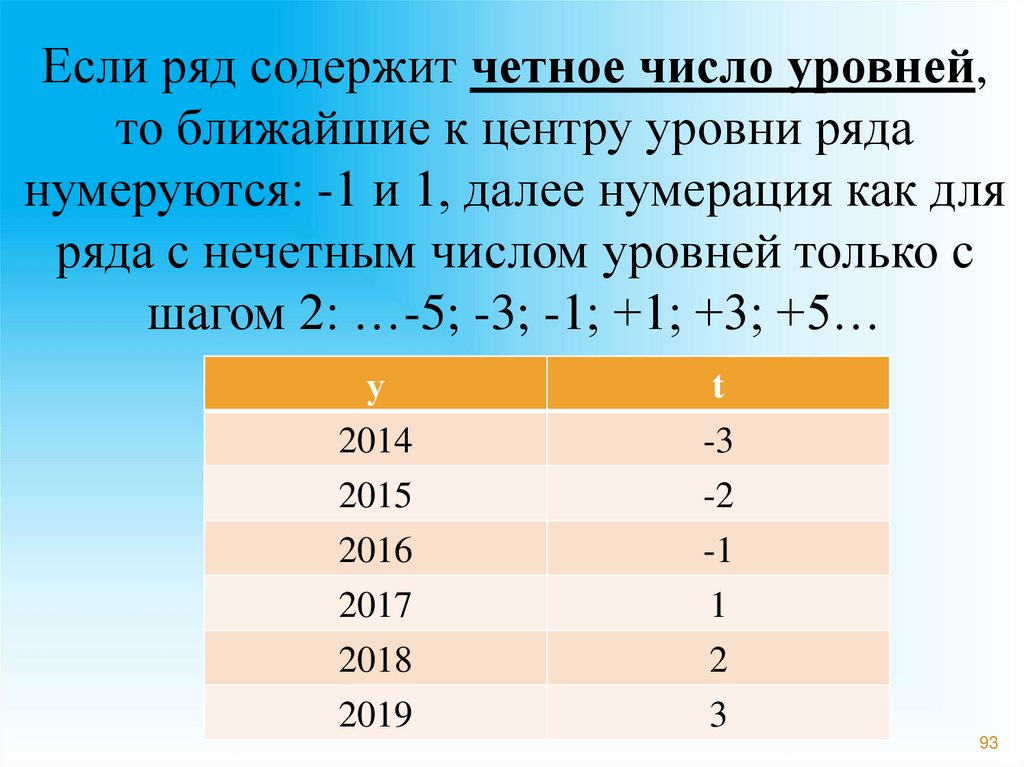
93.
Если ряд содержит четное число уровней,то ближайшие к центру уровни ряда
нумеруются: -1 и 1, далее нумерация как для
ряда с нечетным числом уровней только с
шагом 2: …-5; -3; -1; +1; +3; +5…
у
2014
2015
2016
2017
2018
2019
t
-3
-2
-1
1
2
3
93
94.
a n yty
a
t
n
(y t)
b t (y t) b
t
t
2
t
2
94
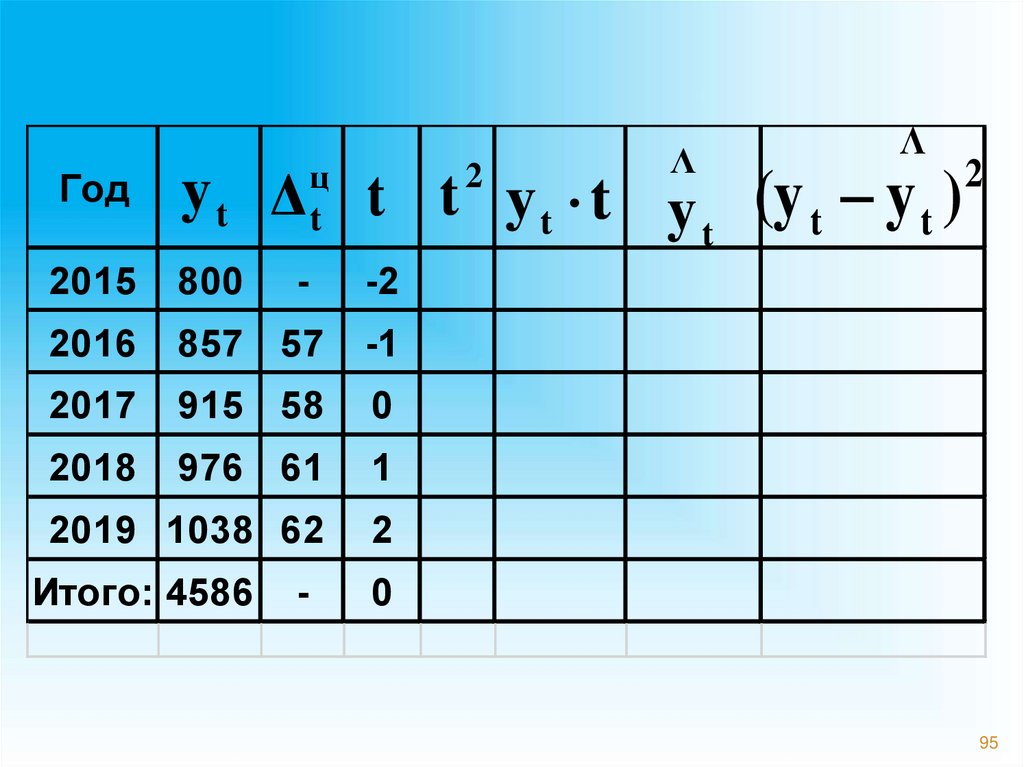
95.
ΛΛ
Год
y t Δ t t y t t y (y t y t )
t
2015
800
-
-2
2016
857 57
-1
2017
915 58
0
2018
976 61
1
2019 1038 62
2
Итого: 4586
0
ц
t
-
2
2
95
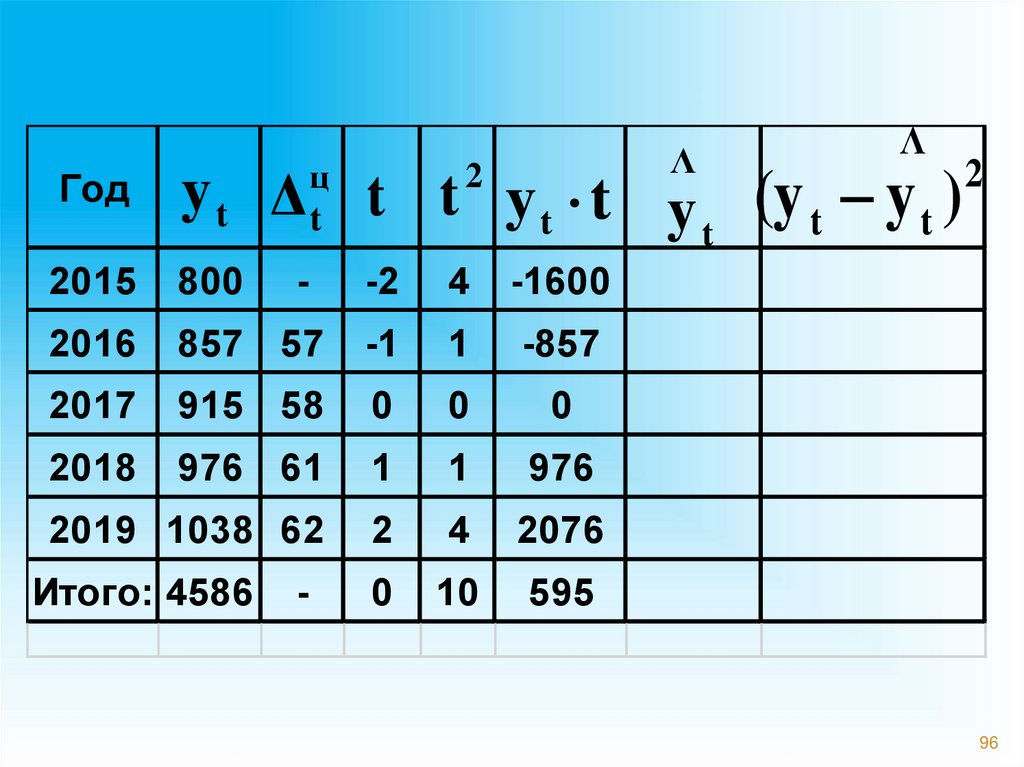
96.
ΛΛ
Год
y t Δ t t y t t y (y t y t )
t
2015
800
-
-2
4
-1600
2016
857 57
-1
1
-857
2017
915 58
0
0
0
2018
976 61
1
1
976
2019 1038 62
2
4
2076
Итого: 4586
0
10
595
ц
t
-
2
2
96
97.
4586a
917,2
5
595
b
59,5
10
Λ
y t 917,2 59,5 t
97
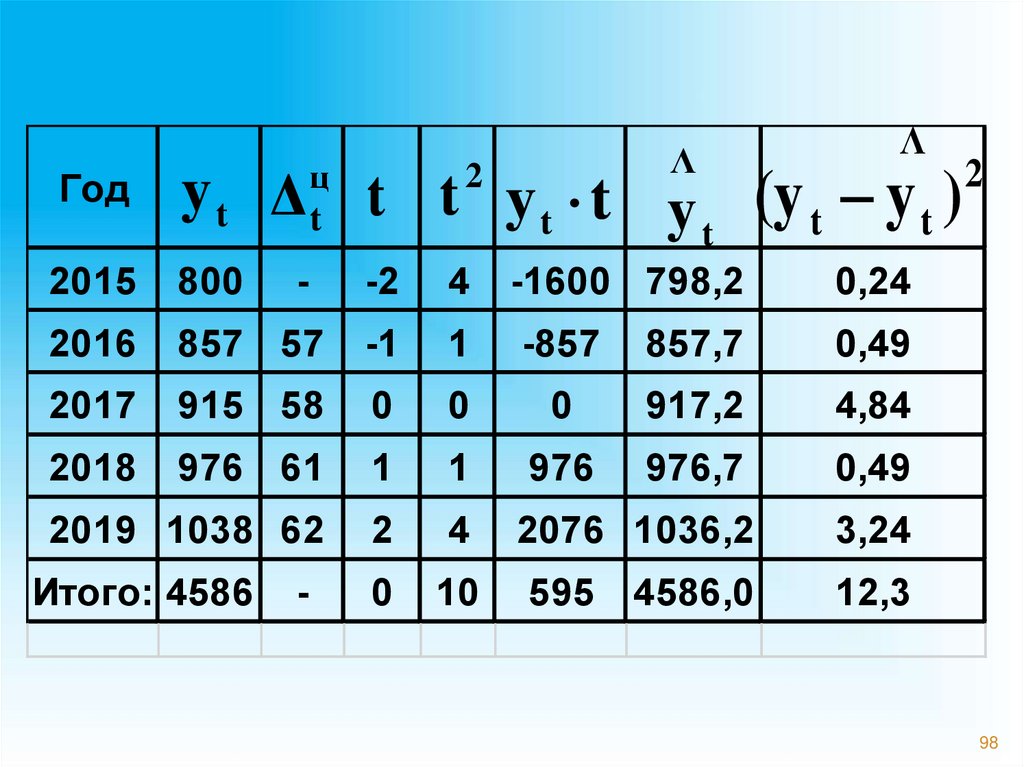
98.
ΛΛ
Год
y t Δ t t y t t y (y t y t )
t
2015
800
-
-2
4
-1600 798,2
0,24
2016
857 57
-1
1
-857
857,7
0,49
2017
915 58
0
0
0
917,2
4,84
2018
976 61
1
1
976
976,7
0,49
2019 1038 62
2
4
2076 1036,2
3,24
Итого: 4586
0
10
595
12,3
ц
t
-
2
4586,0
2
98
99.
После расчета основной тенденции строятграфик, где изображают фактические и
теоретические уровни ряда
Основная тенденция (тренд) показывает
воздействие систематических факторов на
уровень ряда.
Колеблемость уровней около тренда
объясняется воздействием циклических и
случайных факторов, она измеряется по формуле
среднего
квадратического
отклонения
и
коэффициента вариации.
100.
Абсолютную величину колеблемости уровнейряда
около
тренда
измеряют
с
помощью
среднеквадратического отклонения:
Относительной мерой колеблемости является
коэффициент вариации:
101. Ошибка аппроксимации (колеблемость уровней ряда около тренда)
yt)
y
y
(
t
2
n
=1.57
101
102. Относительная мера колеблемости
Vyt
1.57 / 917.2 0.0017
y
или 0,17%
102
103.
Выравнивание по параболе второгопорядка:
Λ
y a b t c t ,
2
где b – скорость изменения уровней
ряда динамики
c – ускорение
103
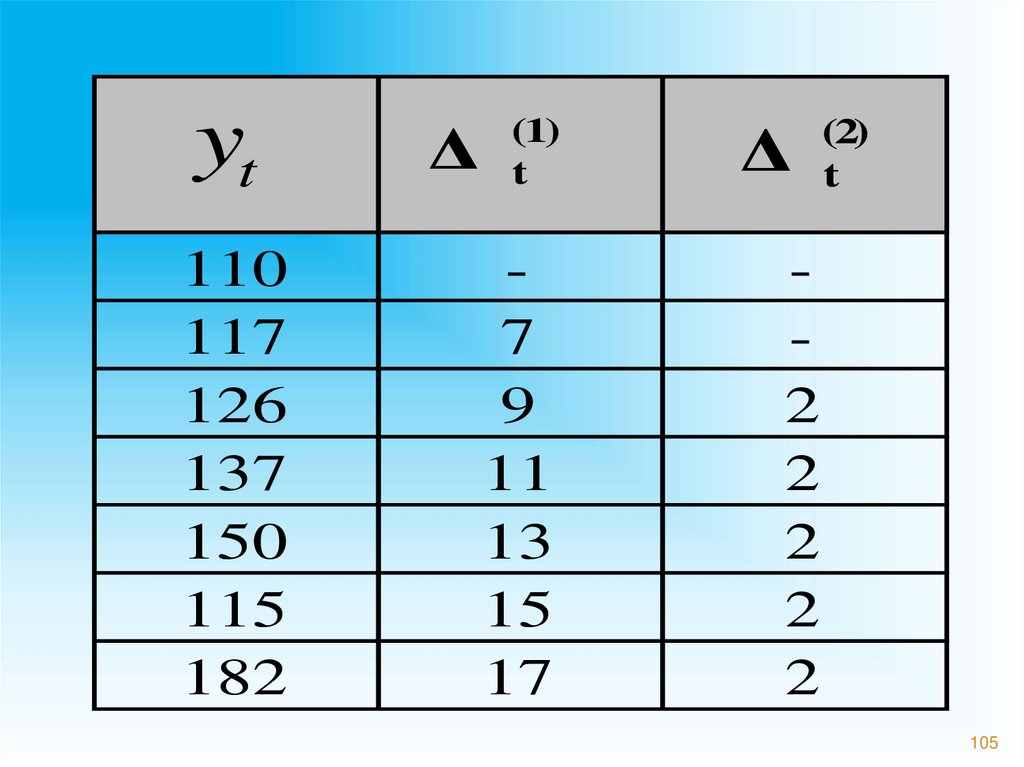
104.
Выравнивание по параболе второгопорядка производится, когда
предварительный анализ показывает, что
вторые разности примерно равны между
собой
(1)
Δ t y t y t 1 - первая разность;
Δ
(2)
t
Δ Δ
(1)
t
(1)
t 1
- вторая разность
104
105.
yt110
117
126
137
150
115
182
Δ
(1)
t
7
9
11
13
15
17
Δ
(2)
t
2
2
2
2
2
105
106.
Для определения параметровприменяется метод наименьших
квадратов:
a n b t c t yt
2
a t b t c t (y t t)
2
3
a t b t c t (y t t )
2
3
4
2
106
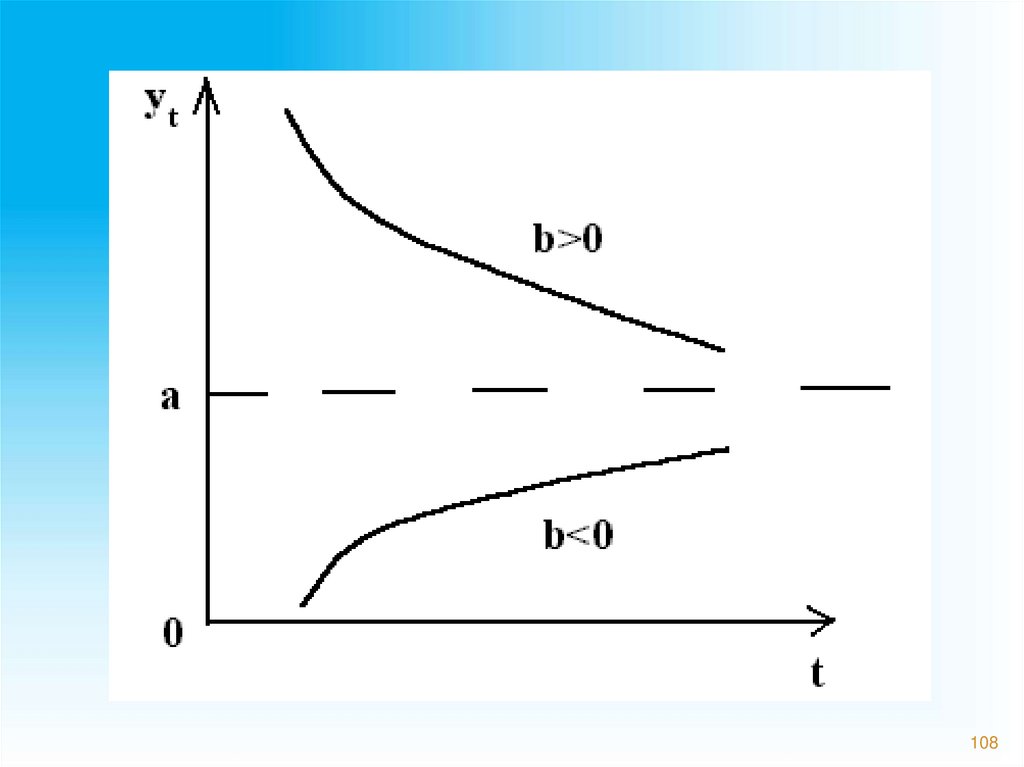
107.
Выравнивание по гиперболеприменяется в тех случаях, когда в
развитии ряда динамики происходит
насыщение
Λ
b
y a
t
107
108.
108109.
Для определения параметровиспользуется МНК:
1
a n b yt
t
yt
1
1
a b 2
t
t
t
109
110.
Выравнивание ряда динамики при помощипоказательных функций или экспоненты
применяется, когда предварительный анализ
показывает: уровень ряда динамики меняется с
приблизительно одинаковыми цепными
коэффициентами роста. При этом коэффициент
b интерпретируется как средний коэффициент
роста
Λ
yt a b
t
110
111.
Для определения параметров функцияприводится предварительно к линейному
виду при помощи логарифмирования
левой и правой частей уравнения
Λ
lg y lga t lgb
При этом мы находим не a и b,
а lga и lgb
111
112.
n lga t lgb lgy tt lga t lgb (lgy t)
2
t
112
113.
Расчет индексовсезонности
113
114.
Сезонным колебаниям свойственны болееили менее устойчивые изменения уровней ряда
по внутригодовым периодам: месяцам, кварталам.
Сезонные
колебания
устойчивые
изменения уровней ряда с периодичностью,
равной году.
Сезонность – результат влияния природноклиматических
условий,
особенностей
производства и потребления.
Для выявления сезонных колебаний обычно
анализируют месячные и квартальные уровни
ряда динамики за год или несколько лет.
114
115.
Задачи, которые необходимо решить в ходеисследования сезонности:
1. выявить наличие сезонности;
2. численно выразить сезонные колебания;
3. выделить факторы, вызывающие сезонные
колебания;
4. оценить последствия сезонных колебаний;
5. провести математическое моделирование
сезонности.
115
116.
Сезонныйхарактер
явления
—
возрастание или убывание уровней повторяется
регулярно с интервалом в один год (например,
производство молока и мяса по месяцам года,
потребление топлива и электроэнергии для
бытовых нужд, сезонная продажа товаров и т.д.).
116
117.
Приизучении
сезонных
колебаний
используются специальные показатели – индексы
сезонности (Is)
Совокупность
исчисленных
индексов
сезонности
характеризует
сезонную
волну
развития явления во внутригодовой динамике
117
118. Способы расчета индексов сезонности
СПОСОБЫ РАСЧЕТАИНДЕКСОВ СЕЗОННОСТИ
1. Для анализа внутригодовой динамики используют
метод постоянной средней (средней для всех
уровней ряда)
Индексы сезонности рассчитывают по формуле:
– сезонное значение уровня ряда
– среднее значение уровня
119.
Рассчитанныезначения
индекса
сезонности сравниваются со значением 100 %.
Если индекс сезонности превышает 100 % —
это свидетельствует о влиянии сезонного
фактора в сторону увеличения уровней
динамического ряда и наоборот.
119
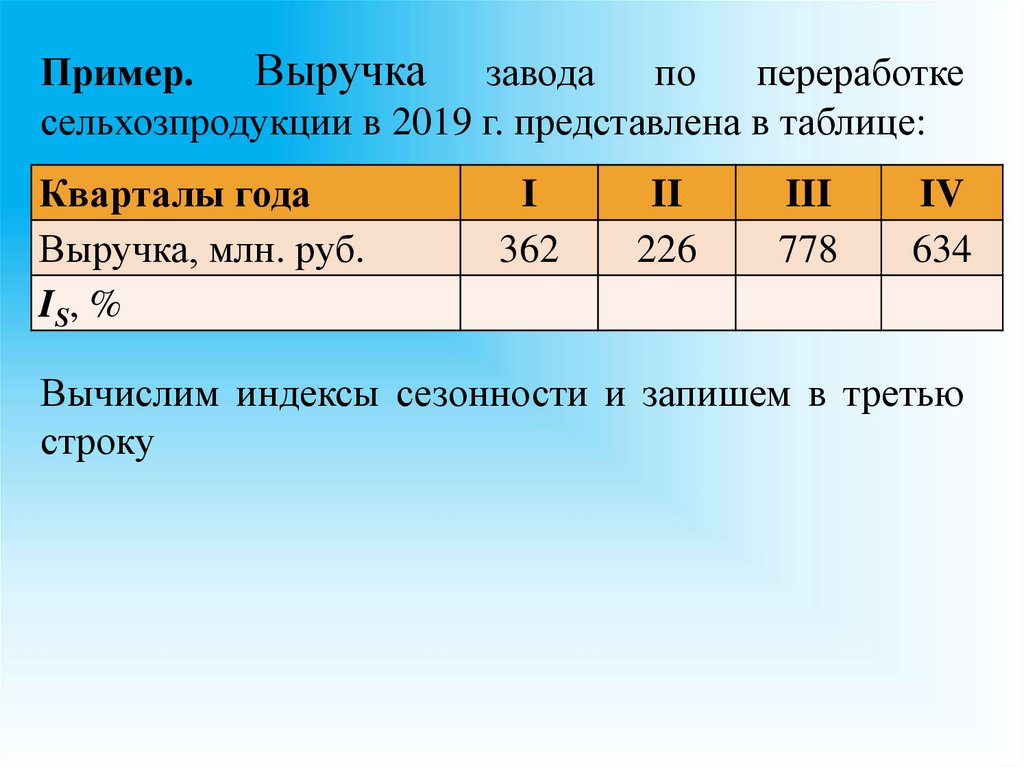
120.
Пример.Выручка завода по переработке
сельхозпродукции в 2019 г. представлена в таблице:
Кварталы года
Выручка, млн. руб.
I S, %
I
362
II
226
III
778
IV
634
Вычислим индексы сезонности и запишем в третью
строку
121.
Кварталы годаВыручка, млн. руб.
I
362
II
226
III
778
IV
634
I S, %
72,4
45,2
155,6 126,8
122.
2. Для анализа закономерности сезонныхколебаний данных одного года недостаточно, поэтому
изучают данные за несколько лет подряд (не менее 3-х):
1) вычисляют среднюю для каждого сезона (месяца,
квартала) за весь период:
n – число лет
2) находят средний уровень за весь изучаемый период
(среднюю из сезонных средних):
m – число сезонов
3) рассчитывают индексы сезонности:
123. Индекс сезонности при относительно неизменном годовом уровне
yiI s 100%
y
123
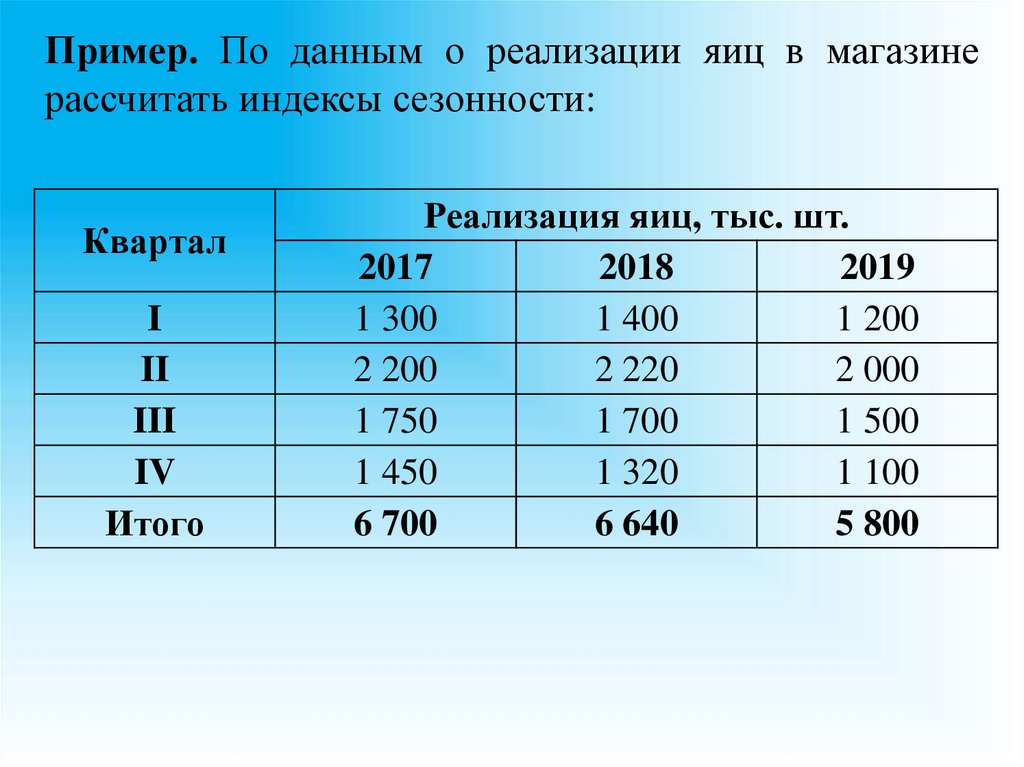
124.
Пример. По данным о реализации яиц в магазинерассчитать индексы сезонности:
Квартал
I
II
III
IV
Итого
Реализация яиц, тыс. шт.
2017
2018
2019
1 300
1 400
1 200
2 200
2 220
2 000
1 750
1 700
1 500
1 450
1 320
1 100
6 700
6 640
5 800
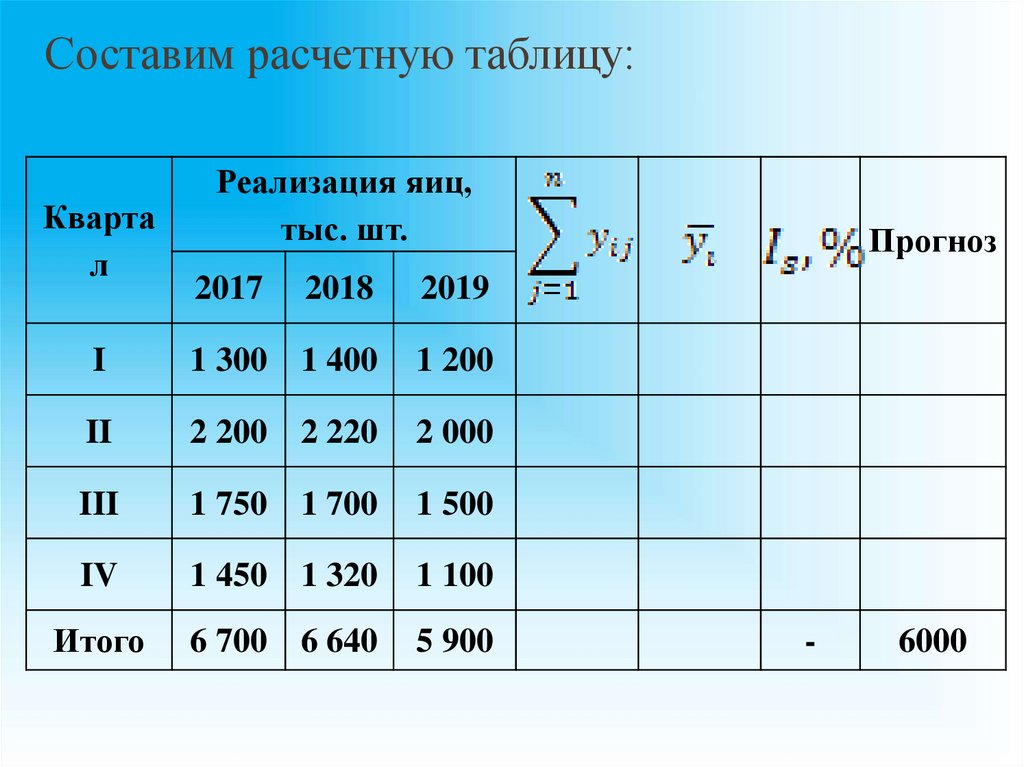
125.
Составим расчетную таблицу:Кварта
л
Реализация яиц,
тыс. шт.
2017
2018
2019
I
1 300 1 400
1 200
II
2 200 2 220
2 000
III
1 750 1 700
1 500
IV
1 450 1 320
1 100
Итого
6 700 6 640
5 900
Прогноз
-
6000
126.
Количество(кварталов) m=4
лет
n=3,
число
Средний уровень за период:
сезонов
127.
Зная годовой прогноз продажи яиц на 2021 г.(6000 тыс. шт.), можно с помощью индексов
сезонности
составить
прогноз
поквартальной
реализации
Например, для первого квартала:
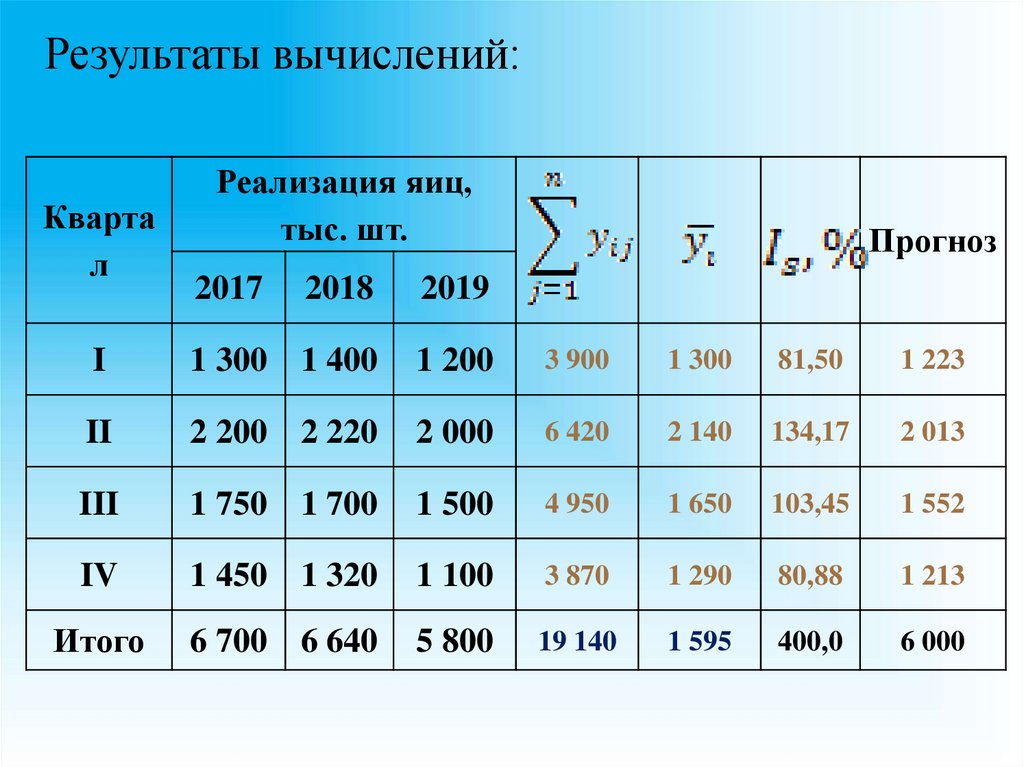
128.
Результаты вычислений:Кварта
л
Реализация яиц,
тыс. шт.
2017
Прогноз
2018
2019
I
1 300 1 400
1 200
3 900
1 300
81,50
1 223
II
2 200 2 220
2 000
6 420
2 140
134,17
2 013
III
1 750 1 700
1 500
4 950
1 650
103,45
1 552
IV
1 450 1 320
1 100
3 870
1 290
80,88
1 213
Итого
6 700 6 640
5 800
19 140
1 595
400,0
6 000
129.
Рассмотренныеспособы
измерения
сезонности используют, если ряд динамики не
содержит ярко выраженной тенденции.
Если ряд динамики содержит ярко
выраженную тенденцию, то до измерения
сезонных колебаний её влияние устраняют
методами сглаживания
130.
3. Ход вычислений прианалитическом
выравнивании:
1) вычислить
для каждого месяца (квартала)
выровненные уровни по соответствующему
аналитическому уравнению на момент времени t;
2) рассчитать отношения фактических уровней (yi) к
соответствующим выравненным уровням в
процентах:
yi
I t 100
yi
131.
3)найти средние арифметические из
одноименных периодов в процентах:
Ii
для
Ii
Ii
n
4)
5)
n – число одноименных периодов (месяцев,
кварталов)
вычислить средний индекс сезонности для всех
месяцев (кварталов)
проверить правильность расчетов:
средний индекс сезонности должен быть равным
100% (средняя арифметическая всех индексов)
сумма полученных помесячных индексов 1200
сумма поквартальных индексов 400
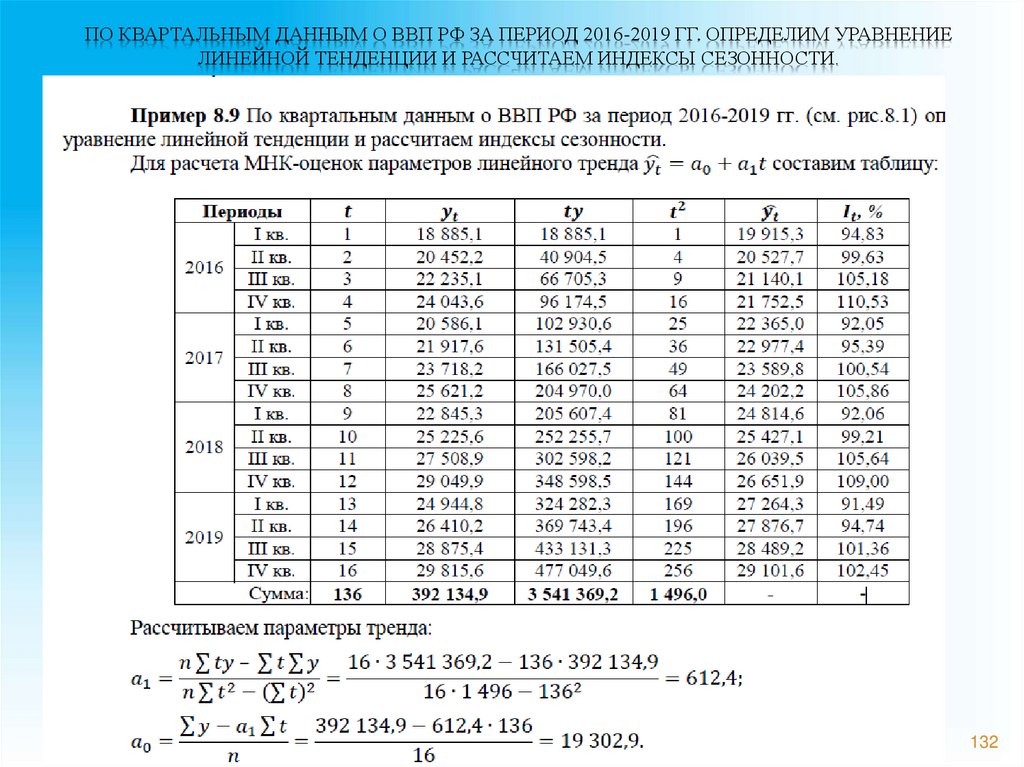
132. По квартальным данным о ВВП РФ за период 2016-2019 гг. определим уравнение линейной тенденции и рассчитаем индексы сезонности.
ПО КВАРТАЛЬНЫМ ДАННЫМ О ВВП РФ ЗА ПЕРИОД 2016-2019 ГГ. ОПРЕДЕЛИМ УРАВНЕНИЕЛИНЕЙНОЙ ТЕНДЕНЦИИ И РАССЧИТАЕМ ИНДЕКСЫ СЕЗОННОСТИ.
132







































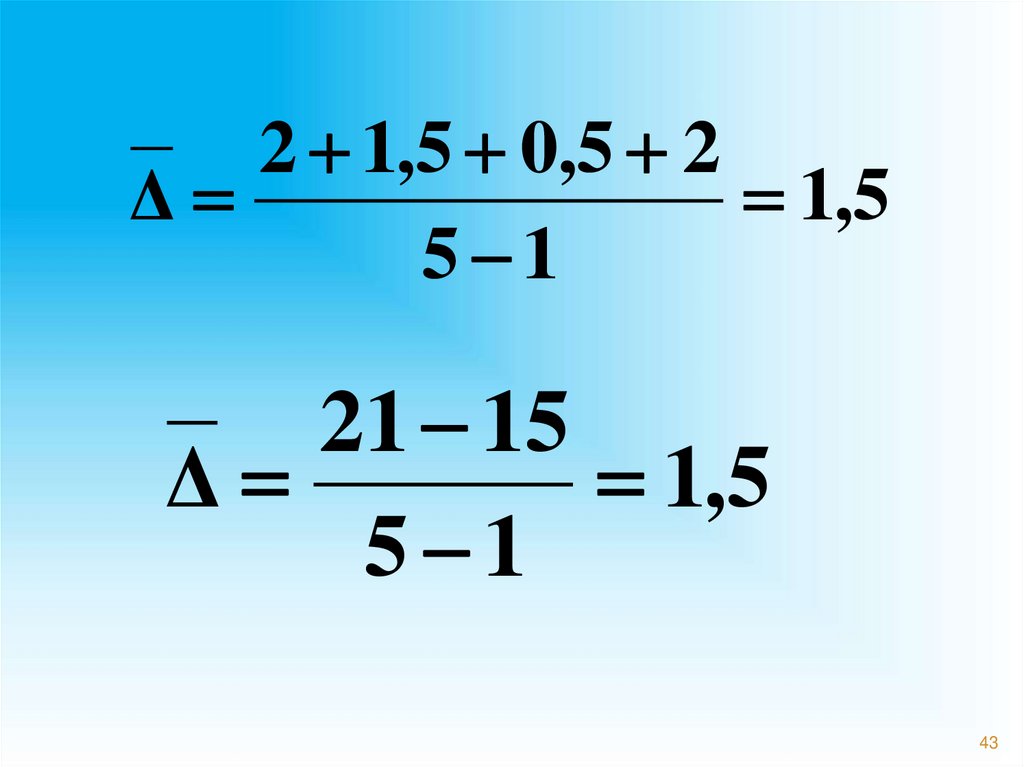


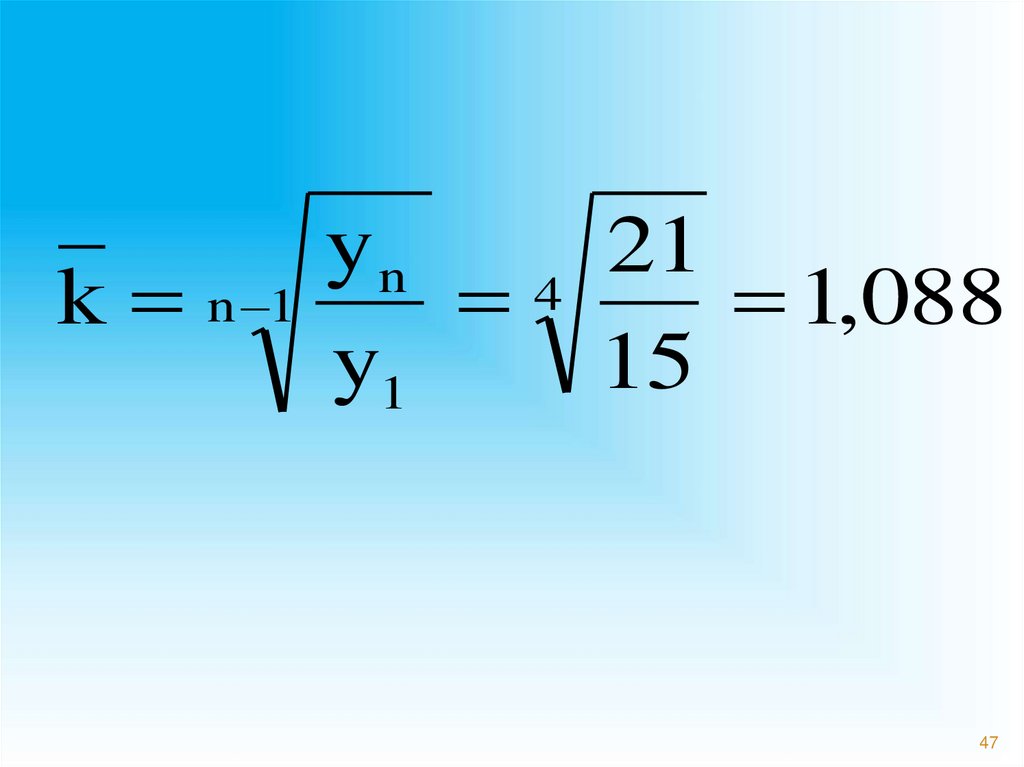


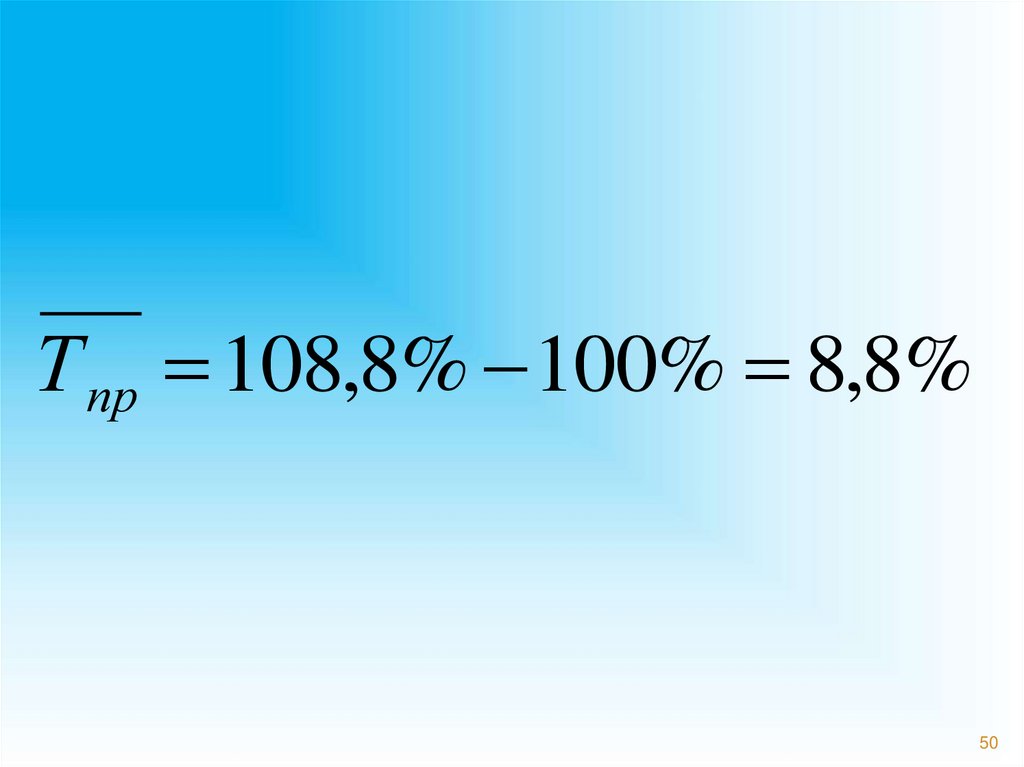





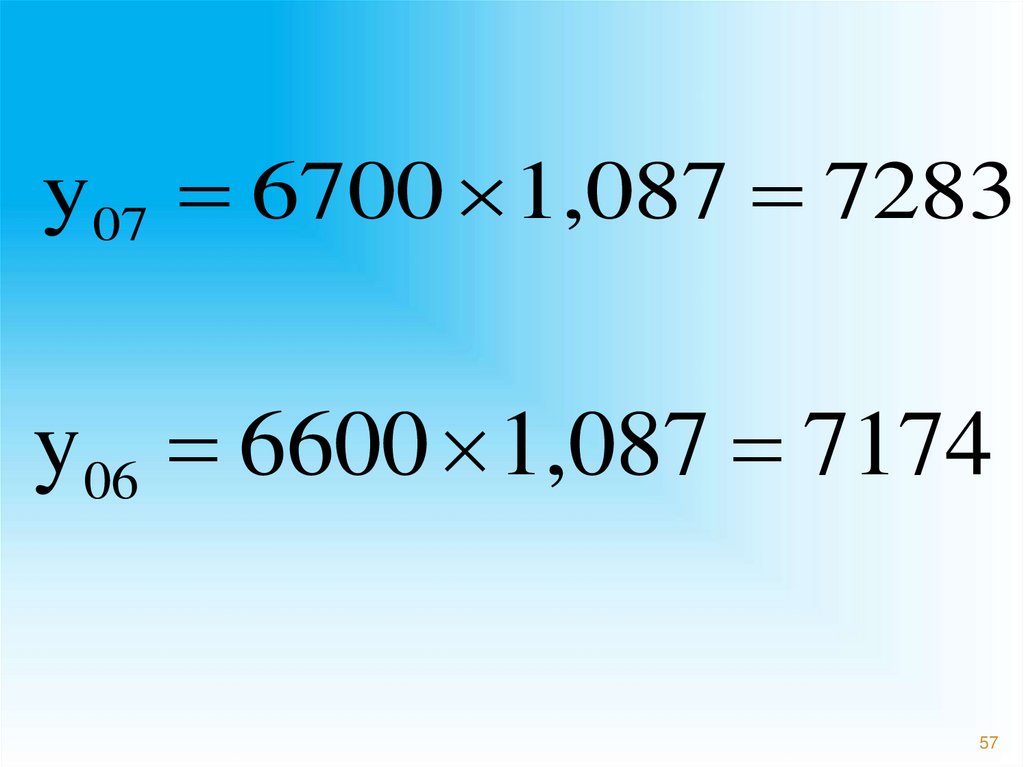






















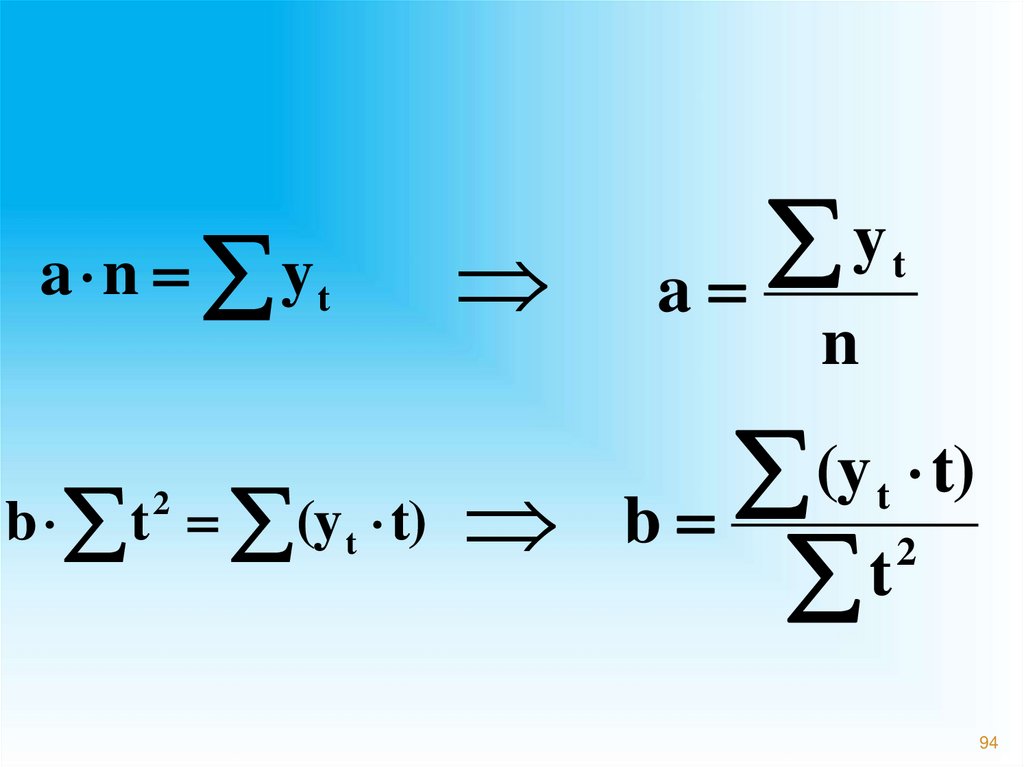
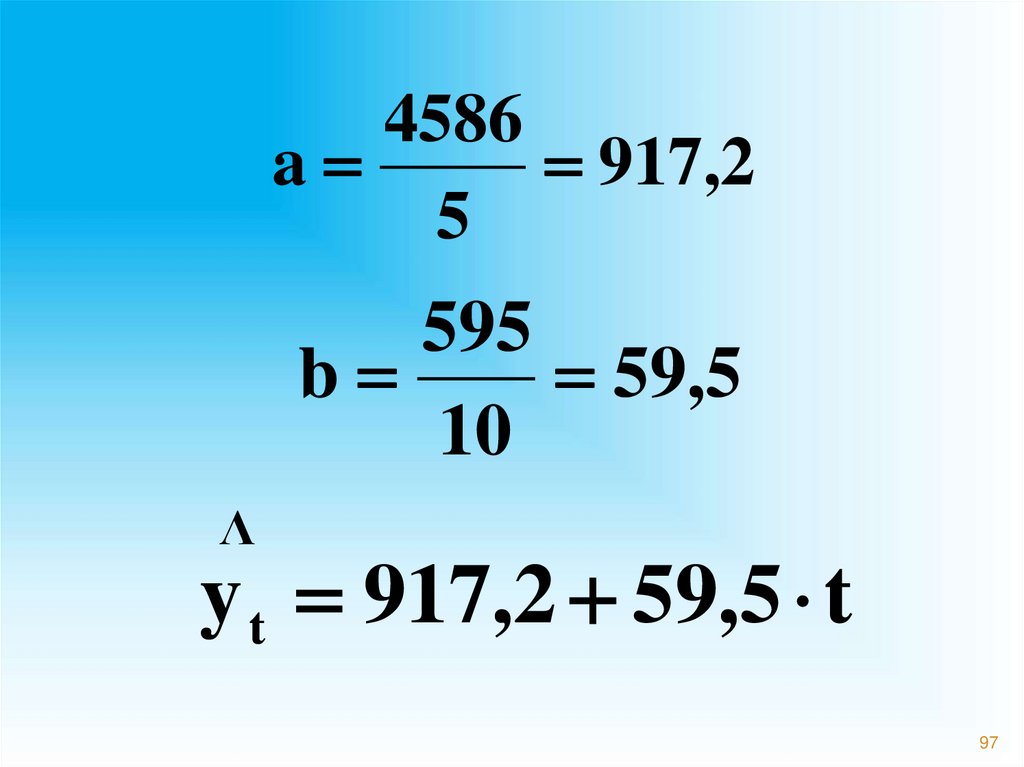








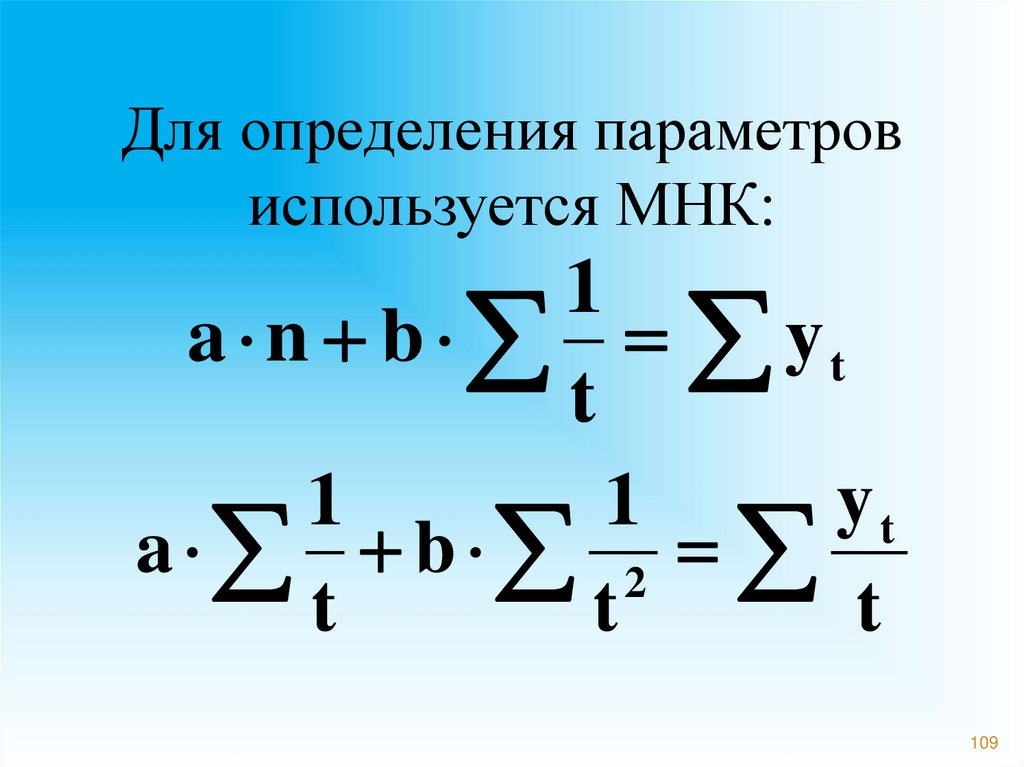


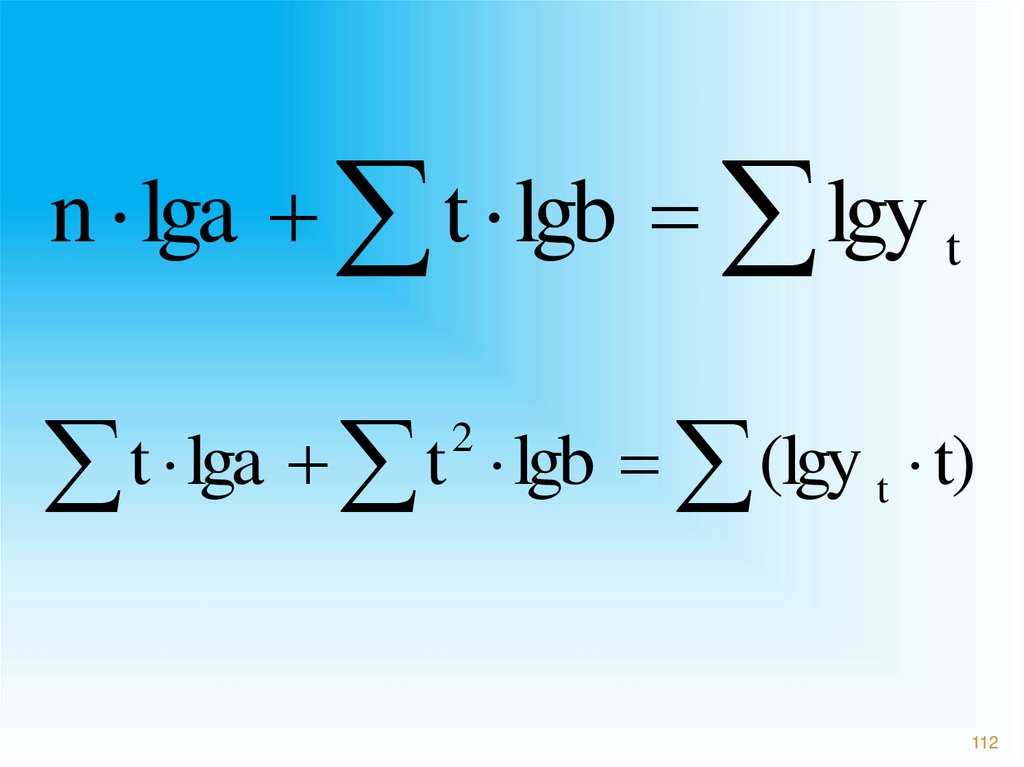
















 Математика
Математика








