070_Графы_Деревья_Бинарные_деревья

1.

ГРАФЫ
ДЕРЕВЬЯ
БИНАРНЫЕ ДЕРЕЬЯ
1

2.

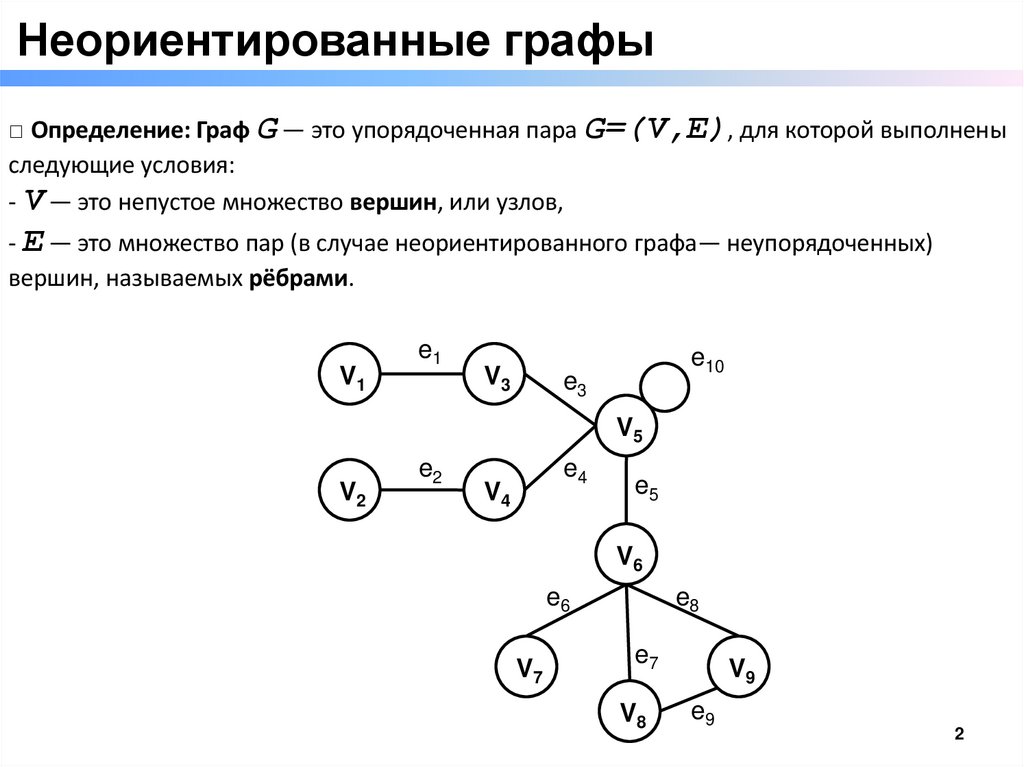
Неориентированные графы
□ Определение: Граф G — это упорядоченная пара G=(V,E), для которой выполнены
следующие условия:
- V — это непустое множество вершин, или узлов,
- E — это множество пар (в случае неориентированного графа— неупорядоченных)
вершин, называемых рёбрами.
V1
e1
V3
e10
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
2

3.

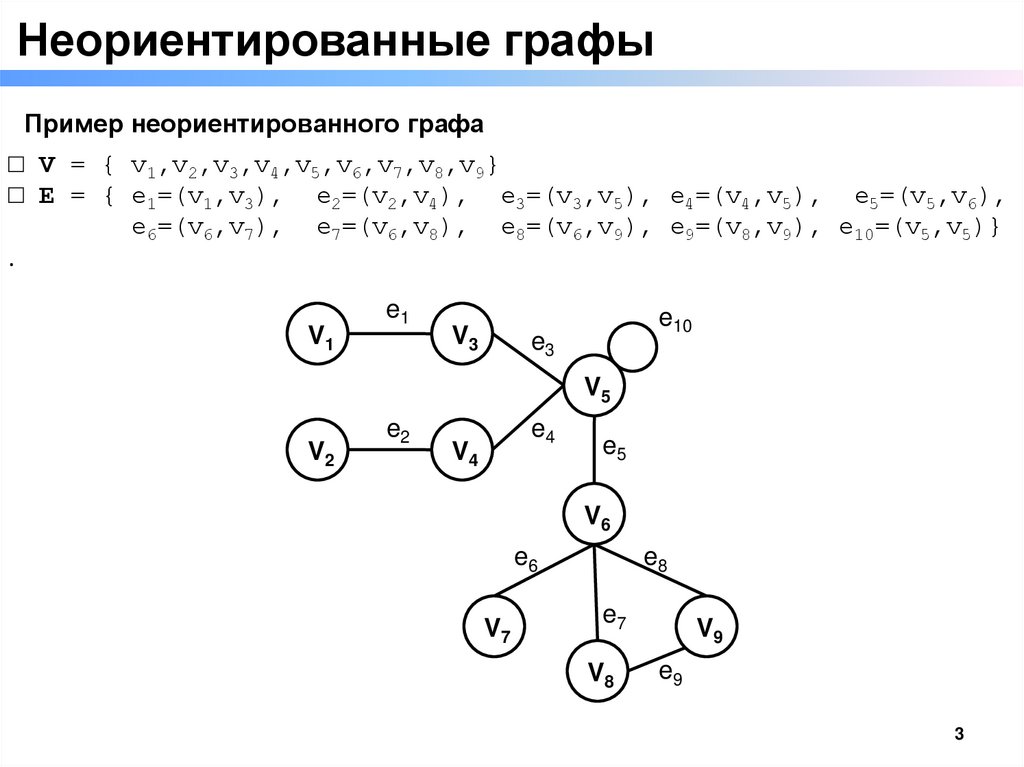
Неориентированные графы
Пример неориентированного графа
□ V = { v1,v2,v3,v4,v5,v6,v7,v8,v9}
□ E = { e1=(v1,v3), e2=(v2,v4), e3=(v3,v5), e4=(v4,v5), e5=(v5,v6),
e6=(v6,v7), e7=(v6,v8), e8=(v6,v9), e9=(v8,v9), e10=(v5,v5)}
.
V1
e1
V3
e10
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
3

4.

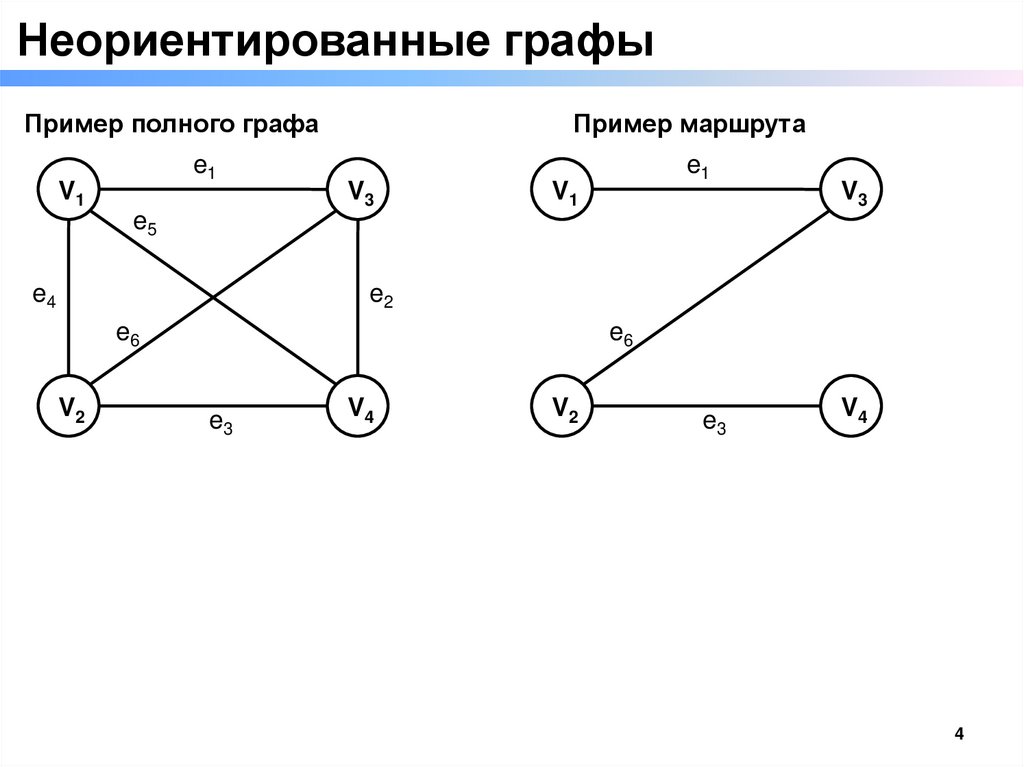
Неориентированные графы
Пример полного графа
e1
V1
Пример маршрута
V3
e1
V1
V3
e5
e4
e2
e6
V2
e6
e3
V4
V2
e3
V4
4

5.

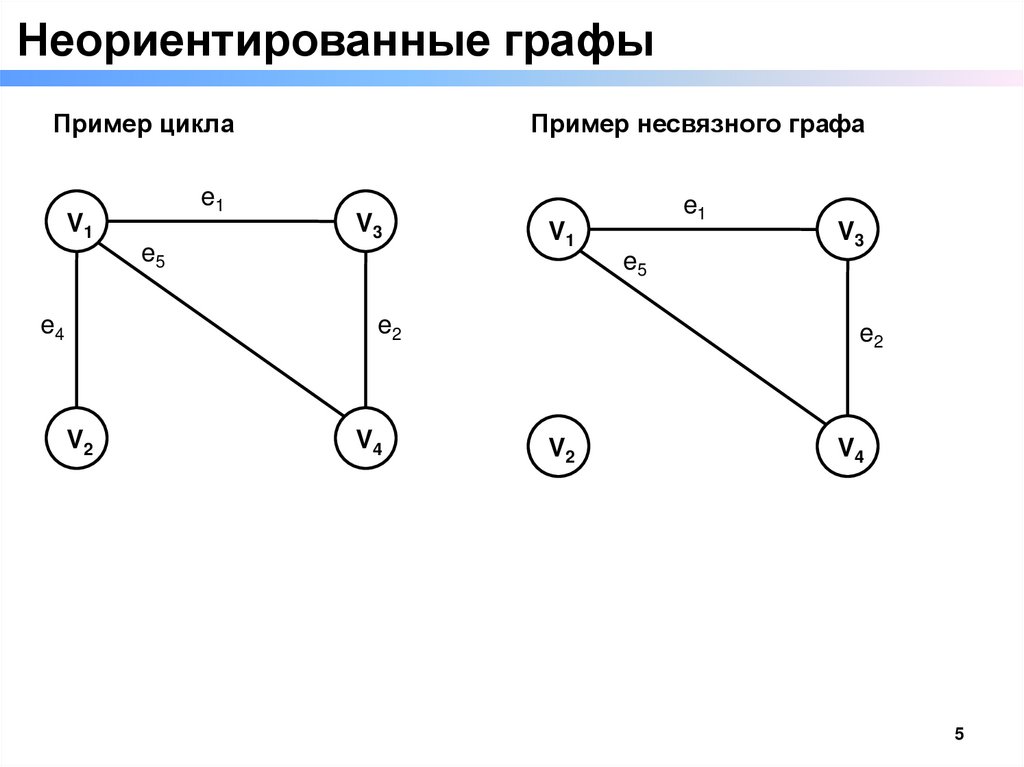
Неориентированные графы
Пример цикла
e1
V1
Пример несвязного графа
V3
e5
e4
V1
V3
e5
e2
V2
e1
V4
e2
V2
V4
5

6.

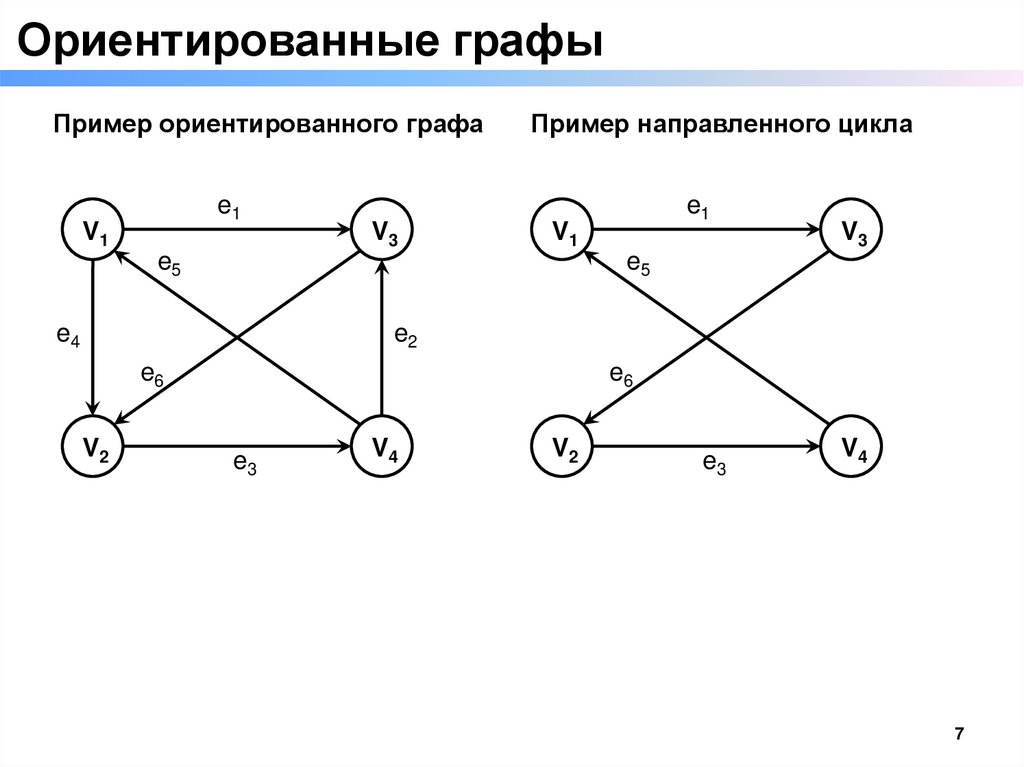
Ориентированные графы
□ Ориентированный граф — это просто граф в котором
ребра между вершинами имеют направление.
□ Каждое ребро — это один путь от вершины-источника до
вершины назначения.
□ Ребро определяется как соединение между парой вершин.
□ В ориентированном графе очень важен порядок пары —
обычно ребро (v,u) проходится только от v до u.
6

7.

Ориентированные графы
Пример ориентированного графа
e1
V1
V3
Пример направленного цикла
e1
V1
e5
V3
e5
e4
e2
e6
V2
e6
e3
V4
V2
e3
V4
7

8.

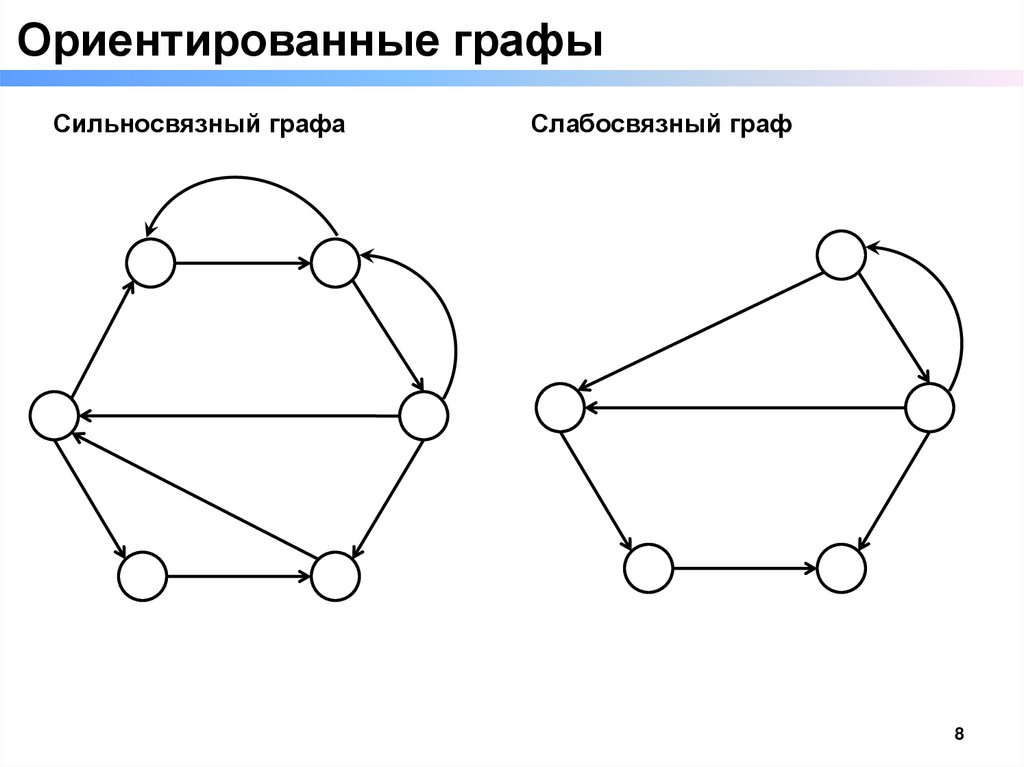
Ориентированные графы
Сильносвязный графа
Слабосвязный граф
8

9.

Методы представления графов
Матрица смежности
Матрица инцидентности
Список смежных вершин
9

10.

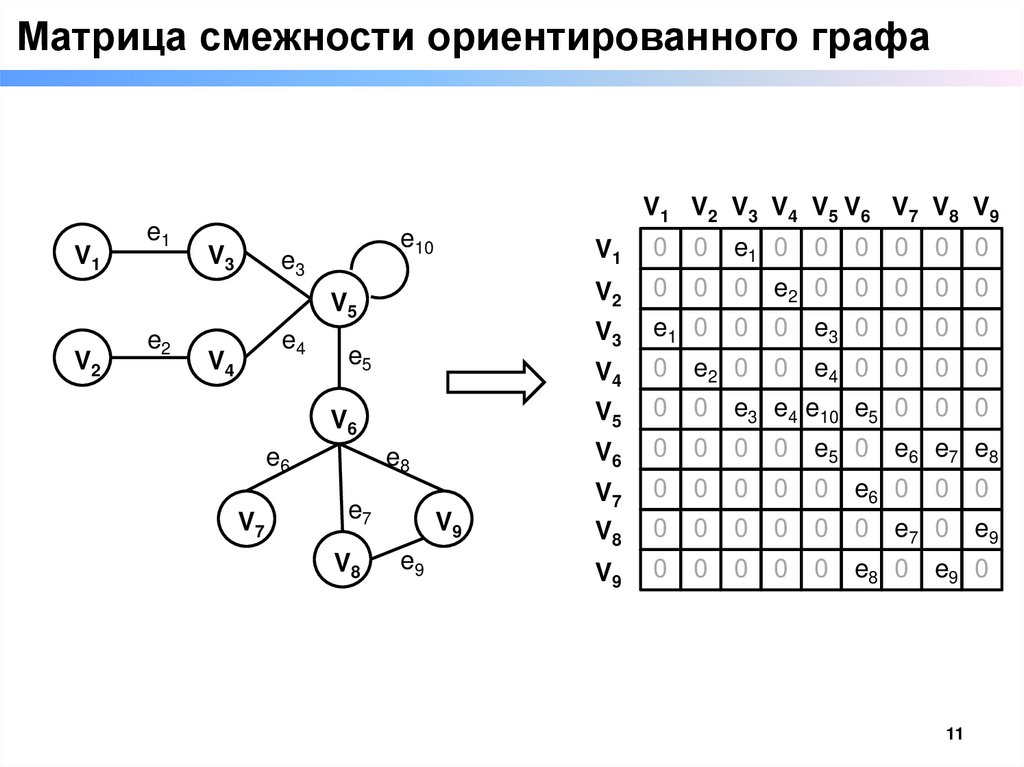
Матрица смежности
□ Любой граф G = (V,E) с М вершинами может быть
представлен матрицей размера М х М при условии, что
вершинам G приписаны произвольные метки.
□ Если вершины G обозначены v1, v2 ..., vM то элементы
aij матрицы смежности А определяются следующим
образом:
ek (vi , v j ) если v i и v j смежные
a ij
если v i и v j не смежные
0
10

11.

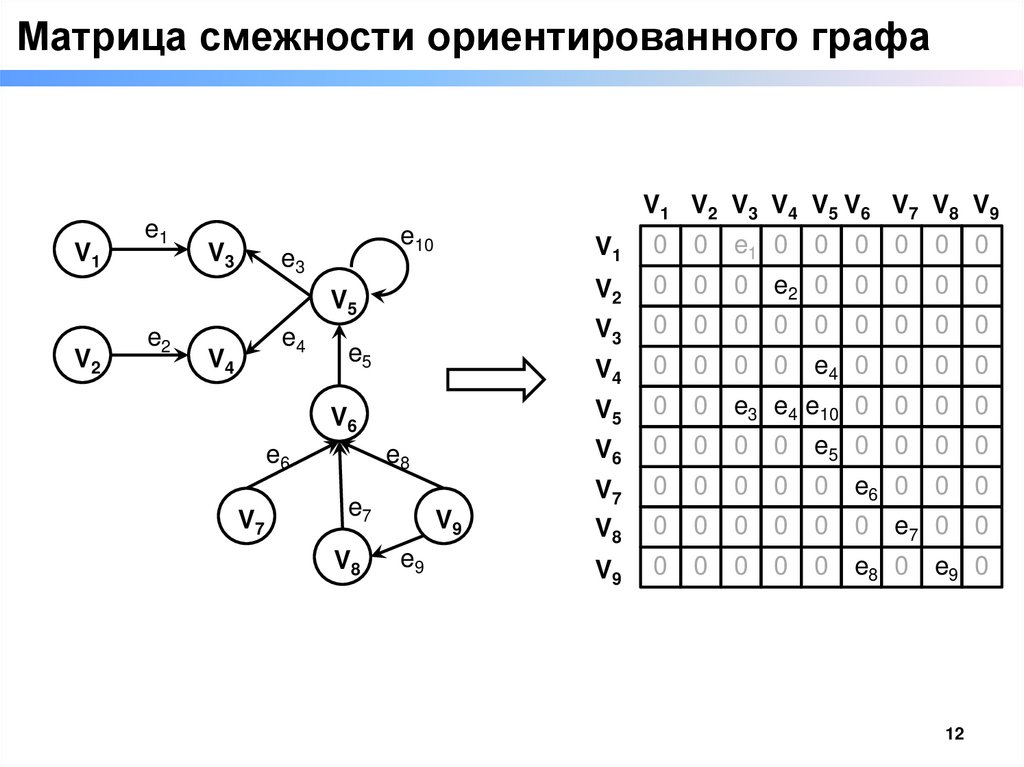
Матрица смежности ориентированного графа
V1
e1
V1 V2 V3 V4 V5 V6 V7 V8 V9
V3
e10
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
V1
0
0
e1 0
0
0
0
0
0
V2
0
0
0
e2 0
0
0
0
0
V3
e1 0
0
0
e3 0
0
0
0
V4
0
e2 0
0
e4 0
0
0
0
V5
0
0
e3 e4 e10 e5 0
0
0
V6
0
0
0
0
e5 0
V7
V8
0
0
0
0
0
e6 0
0
0
0
0
0
0
V9
0
0
0
0
0
e8 0
e6 e7 e8
0
0
e7 0
e9
e9 0
11

12.

Матрица смежности ориентированного графа
V1
e1
V1 V2 V3 V4 V5 V6 V7 V8 V9
V3
e10
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
V1
0
0
e1 0
0
0
0
0
0
V2
0
0
0
e2 0
0
0
0
0
V3
0
0
0
0
0
0
0
0
0
V4
0
0
0
0
e4 0
0
0
0
V5
0
0
e3 e4 e10 0
0
0
0
V6
0
0
0
0
e5 0
0
0
0
V7
V8
0
0
0
0
0
e6 0
0
0
0
0
0
0
0
0
e7 0
0
V9
0
0
0
0
0
e8 0
e9 0
12

13.

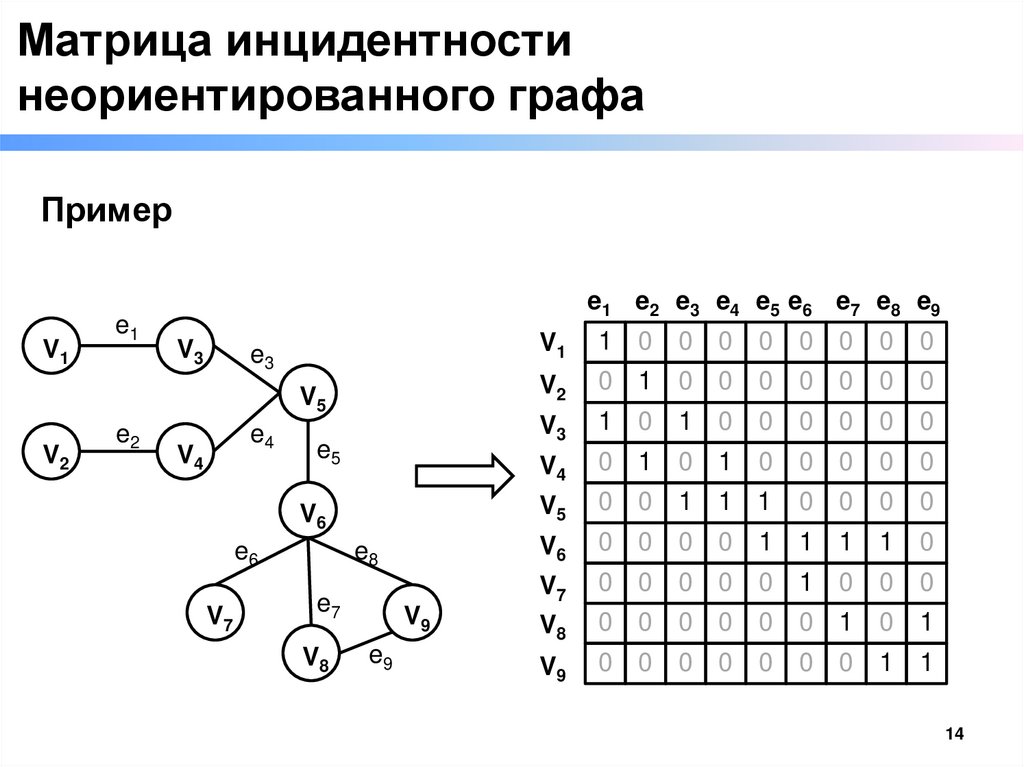
Матрица инцидентности
неориентированного графа
□ Если у неориентированного графа G вершины V обозначены
v1, v2 ..., vM, а ребра E — метками e1, e2,…,eN, то
матрица инцидентности определяется следующим образом:
1, если ребро e j инцидентно вершине vi
bij
0, если ребро e j не инцидентно вершине vi
□ Особенности
• В каждом столбце должны стоять две единицы, а все остальные символы - нули
• Не используется для графов с петлями, так как у петель одна вершина является и
началом, и концом.
13

14.

Матрица инцидентности
неориентированного графа
Пример
V1
e1
e1 e2 e3 e4 e5 e6 e7 e8 e9
V3
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
V1
1
0
0
0
0
0
0
0
0
V2
0
1
0
0
0
0
0
0
0
V3
1
0
1
0
0
0
0
0
0
V4
0
1
0
1
0
0
0
0
0
V5
0
0
1
1 1
0
0
0
0
V6
0
0
0
0
1
1
1
1
0
V7
V8
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
1
V9
0
0
0
0
0
0
0
1
1
14

15.

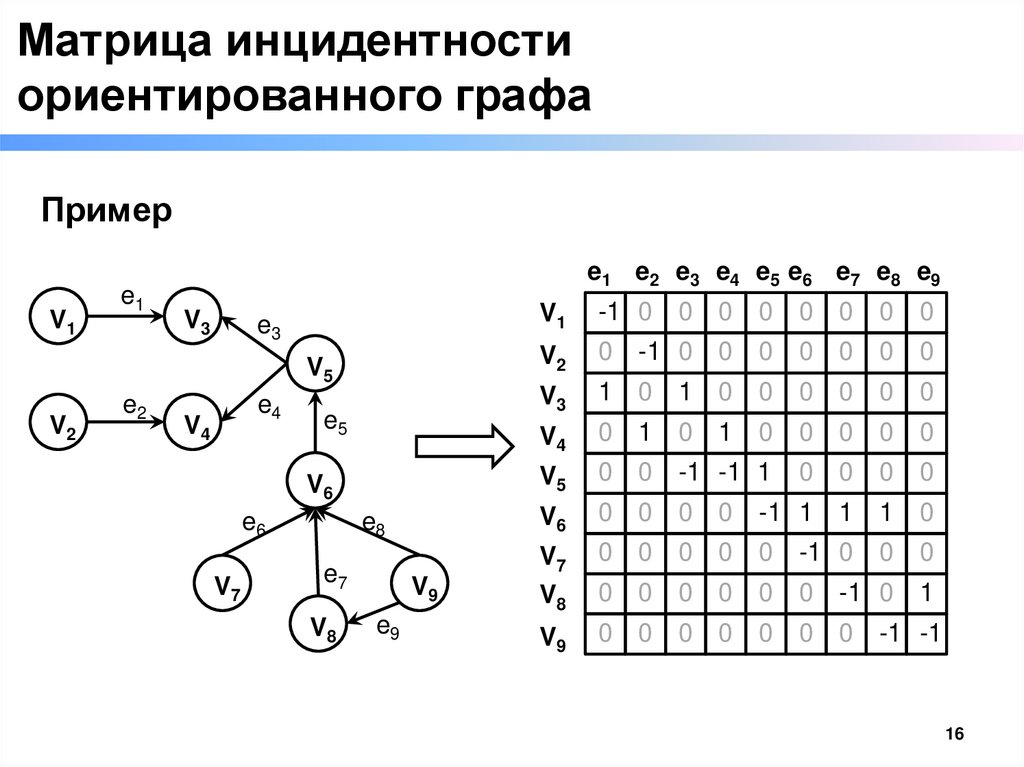
Матрица инцидентности
ориентированного графа
□ Если у ориентированного графа G вершины V обозначены
v1, v2 ..., vM, а ребра E — метками e1, e2,…,eN , то матрица
инцидентности определяется следующим образом:
1, если вершина vi начало ребра e j
bij 1, если вершина vi конец ребра e j
0, если вершине v и ребро e не инцидентны
i
j
15

16.

Матрица инцидентности
ориентированного графа
Пример
V1
e1
e1 e2 e3 e4 e5 e6 e7 e8 e9
V3
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
V1
-1 0
0
0
0
0
0
0
0
V2
0
-1 0
0
0
0
0
0
0
V3
1
0
1
0
0
0
0
0
0
V4
0
1
0
1
0
0
0
0
0
V5
0
0
-1 -1 1
0
0
0
0
V6
0
0
0
0
-1 1
1
1
0
V7
V8
0
0
0
0
0
-1 0
0
0
0
0
0
0
0
0
-1 0
1
V9
0
0
0
0
0
0
0
-1 -1
16

17.

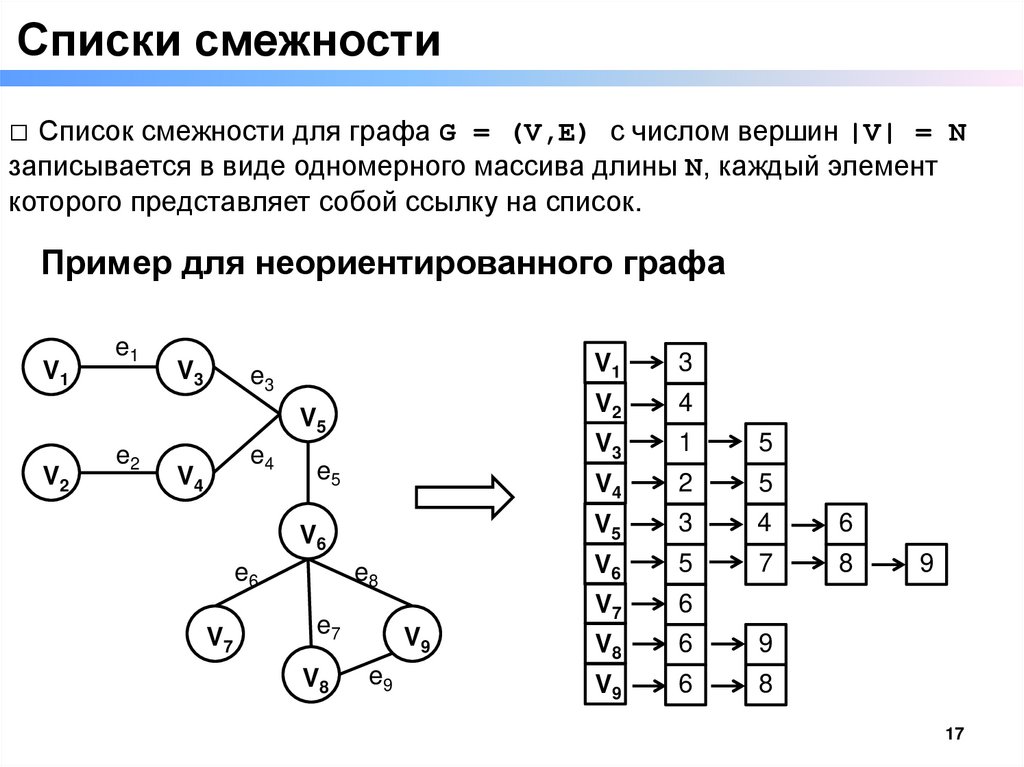
Списки смежности
□ Список смежности для графа G = (V,E) с числом вершин |V| = N
записывается в виде одномерного массива длины N, каждый элемент
которого представляет собой ссылку на список.
Пример для неориентированного графа
V1
e1
V3
e3
V5
V2
e2
e4
V4
e5
V6
e6
V7
e8
e7
V8
V9
e9
V1
3
V2
4
V3
1
5
V4
2
5
V5
3
4
6
V6
5
7
8
V7
6
V8
6
9
V9
6
8
9
17

18.

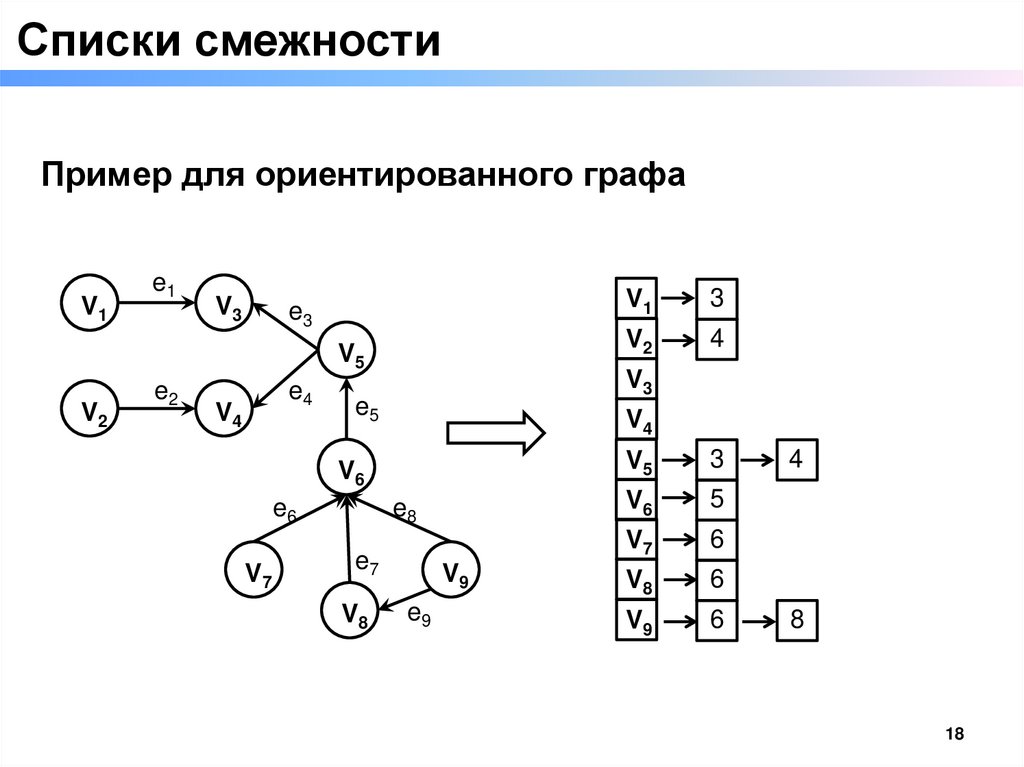
Списки смежности
Пример для ориентированного графа
V1
e1
V3
e3
V5
V2
e2
e4
V4
e8
e7
V8
V2
4
V4
V6
V7
3
V3
e5
e6
V1
V9
e9
V5
3
V6
5
V7
6
V8
6
V9
6
4
8
18

19.

ДЕРЕВЬЯ
19

20.

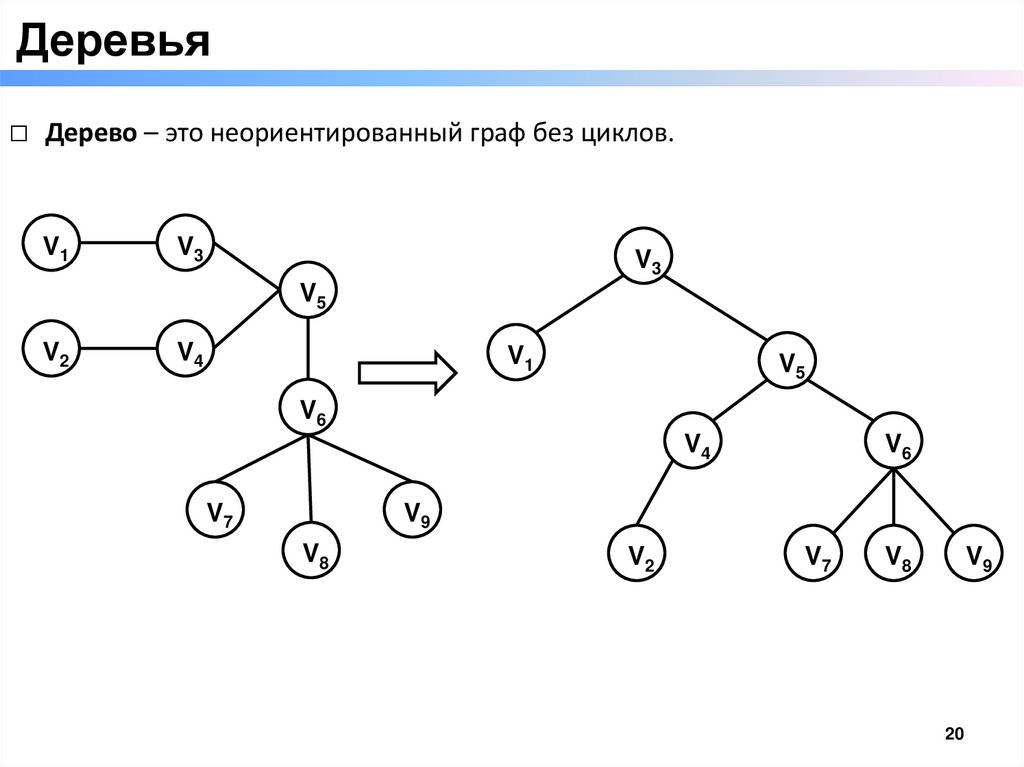
Деревья
□ Дерево – это неориентированный граф без циклов.
V1
V3
V3
V5
V2
V4
V1
V5
V6
V4
V7
V6
V9
V8
V2
V7
V8
V9
20

21.

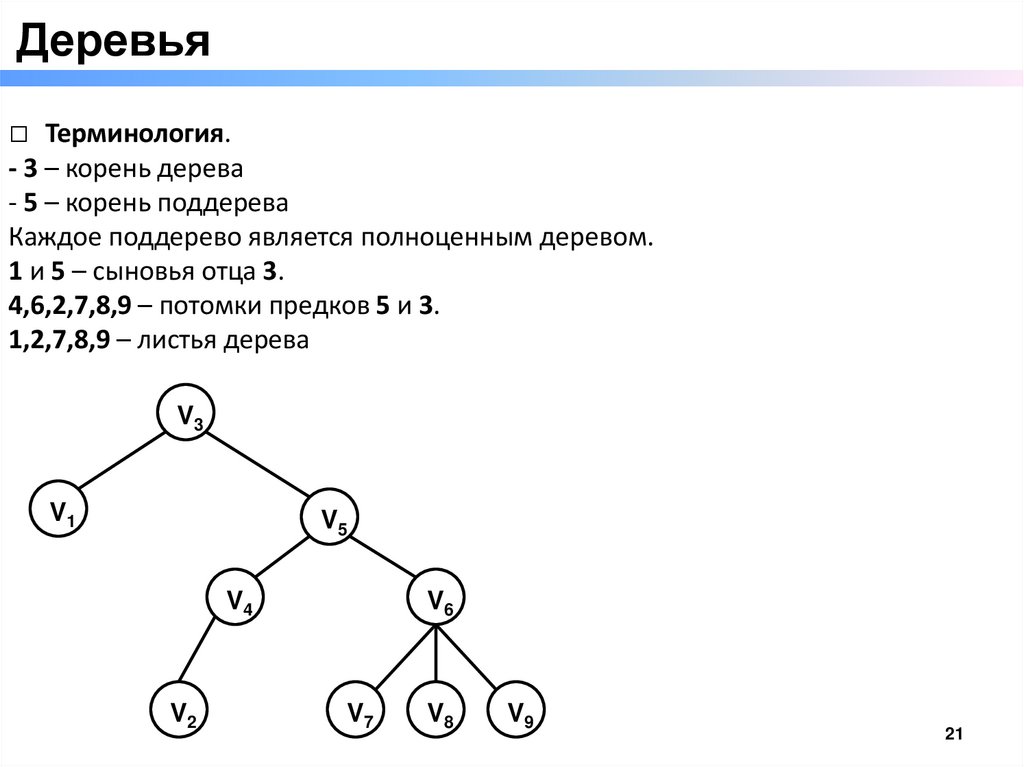
Деревья
□ Терминология.
- 3 – корень дерева
- 5 – корень поддерева
Каждое поддерево является полноценным деревом.
1 и 5 – сыновья отца 3.
4,6,2,7,8,9 – потомки предков 5 и 3.
1,2,7,8,9 – листья дерева
V3
V1
V5
V4
V2
V6
V7
V8
V9
21

22.

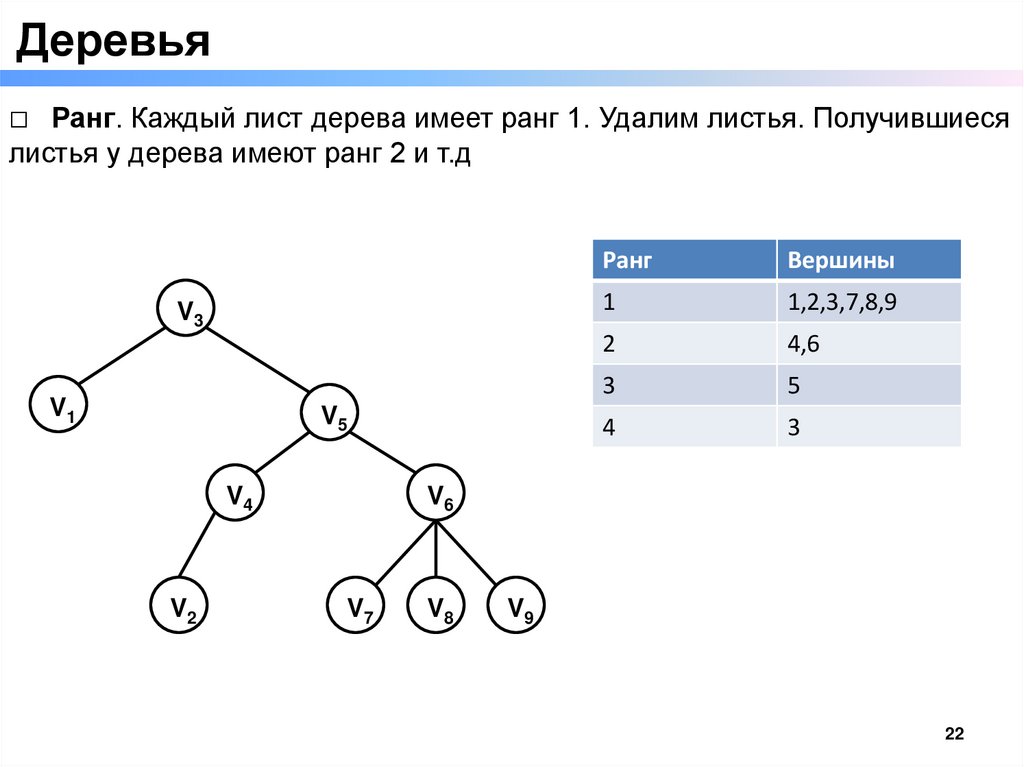
Деревья
□ Ранг. Каждый лист дерева имеет ранг 1. Удалим листья. Получившиеся
листья у дерева имеют ранг 2 и т.д
V3
V1
V5
V4
V2
Ранг
Вершины
1
1,2,3,7,8,9
2
4,6
3
5
4
3
V6
V7
V8
V9
22

23.

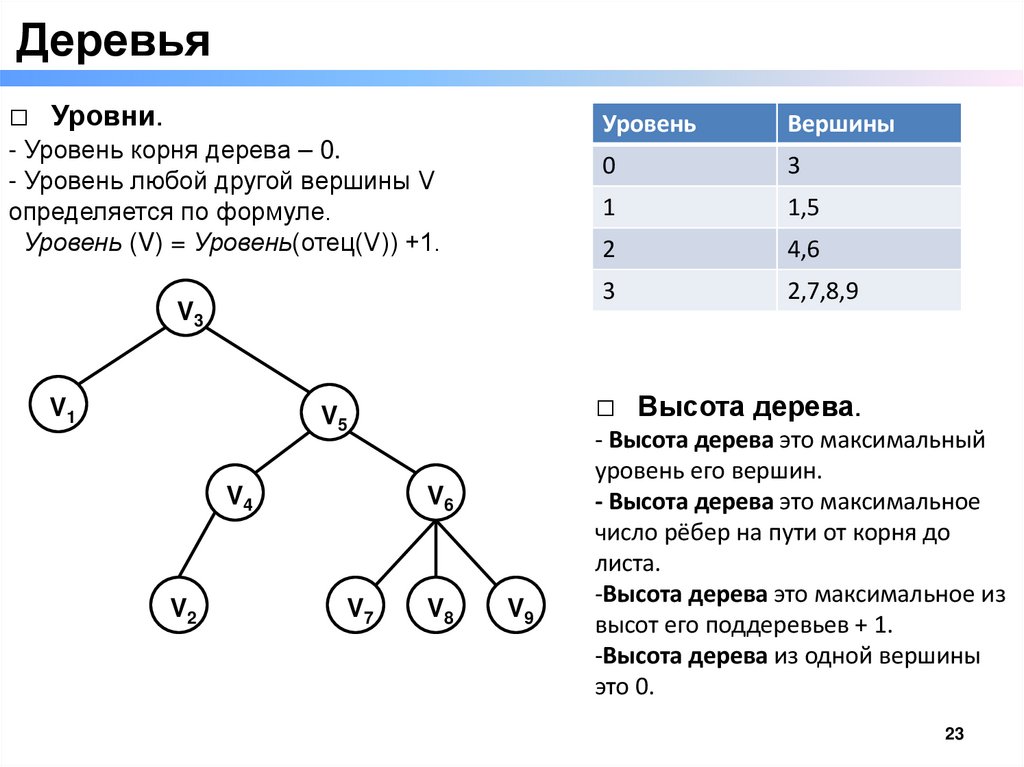
Деревья
□ Уровни.
- Уровень корня дерева – 0.
- Уровень любой другой вершины V
определяется по формуле.
Уровень (V) = Уровень(отец(V)) +1.
V3
V1
V2
V6
V7
Вершины
0
3
1
1,5
2
4,6
3
2,7,8,9
□ Высота дерева.
V5
V4
Уровень
V8
V9
- Высота дерева это максимальный
уровень его вершин.
- Высота дерева это максимальное
число рёбер на пути от корня до
листа.
-Высота дерева это максимальное из
высот его поддеревьев + 1.
-Высота дерева из одной вершины
это 0.
23

24.

Деревья
□ Методы хранения деревьев в памяти.
- Матрица смежности
– аналогично графам
- Матрица инцидентности – аналогично графам
- Списки смежности.
24

25.

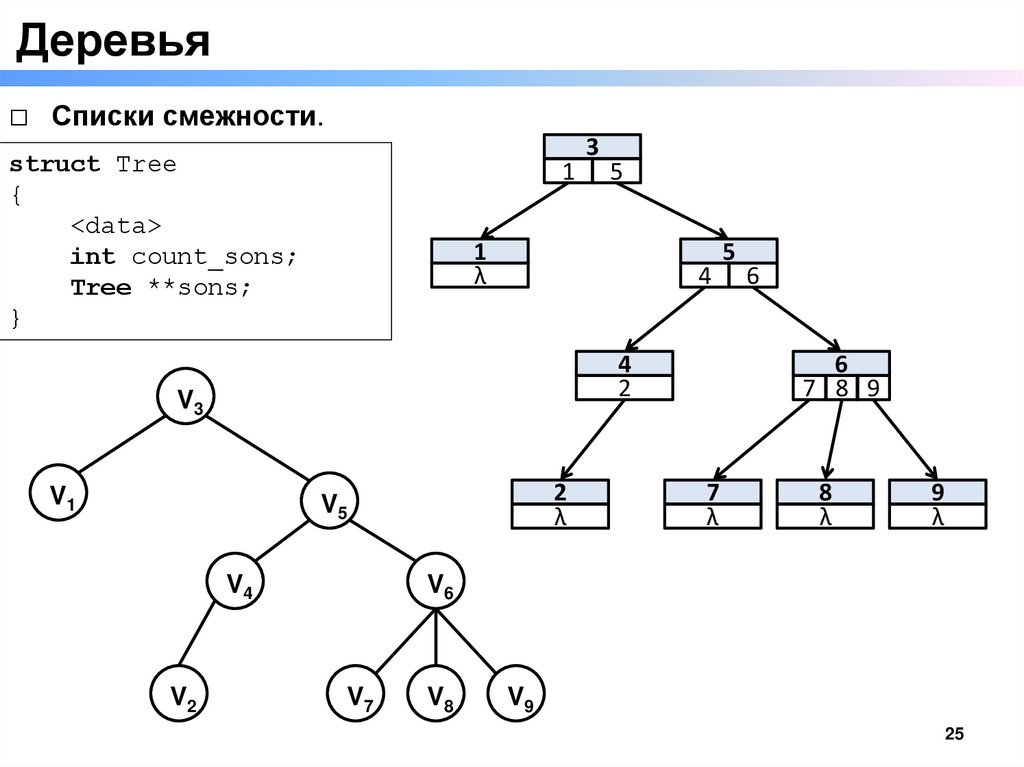
Деревья
□ Списки смежности.
struct Tree
{
<data>
int count_sons;
Tree **sons;
}
1
5
1
λ
4
4
2
V3
V1
2
λ
V5
V4
V2
3
5
6
6
7 8 9
7
λ
8
λ
9
λ
V6
V7
V8
V9
25

26.

БИНАРНЫЕ ДЕРЕВЬЯ
26

27.

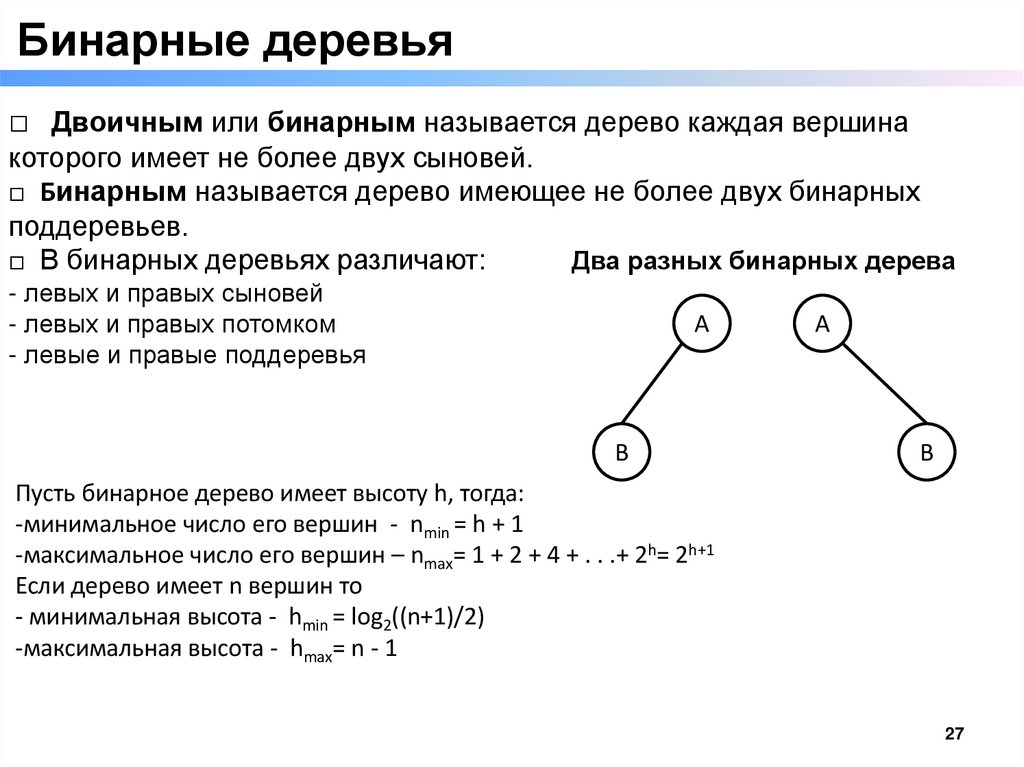
Бинарные деревья
□ Двоичным или бинарным называется дерево каждая вершина
которого имеет не более двух сыновей.
□ Бинарным называется дерево имеющее не более двух бинарных
поддеревьев.
Два разных бинарных дерева
□ В бинарных деревьях различают:
- левых и правых сыновей
- левых и правых потомком
- левые и правые поддеревья
A
B
A
B
Пусть бинарное дерево имеет высоту h, тогда:
-минимальное число его вершин - nmin = h + 1
-максимальное число его вершин – nmax= 1 + 2 + 4 + . . .+ 2h= 2h+1
Если дерево имеет n вершин то
- минимальная высота - hmin = log2((n+1)/2)
-максимальная высота - hmax= n - 1
27

28.

Бинарные деревья
□ Методы хранения бинарных деревьев в памяти.
- Матрица смежности
– аналогично графам
- Матрица инцидентности – аналогично графам
- Списки смежности.
- Двумерные таблицы 2*N
- Одномерные массивы
28

29.

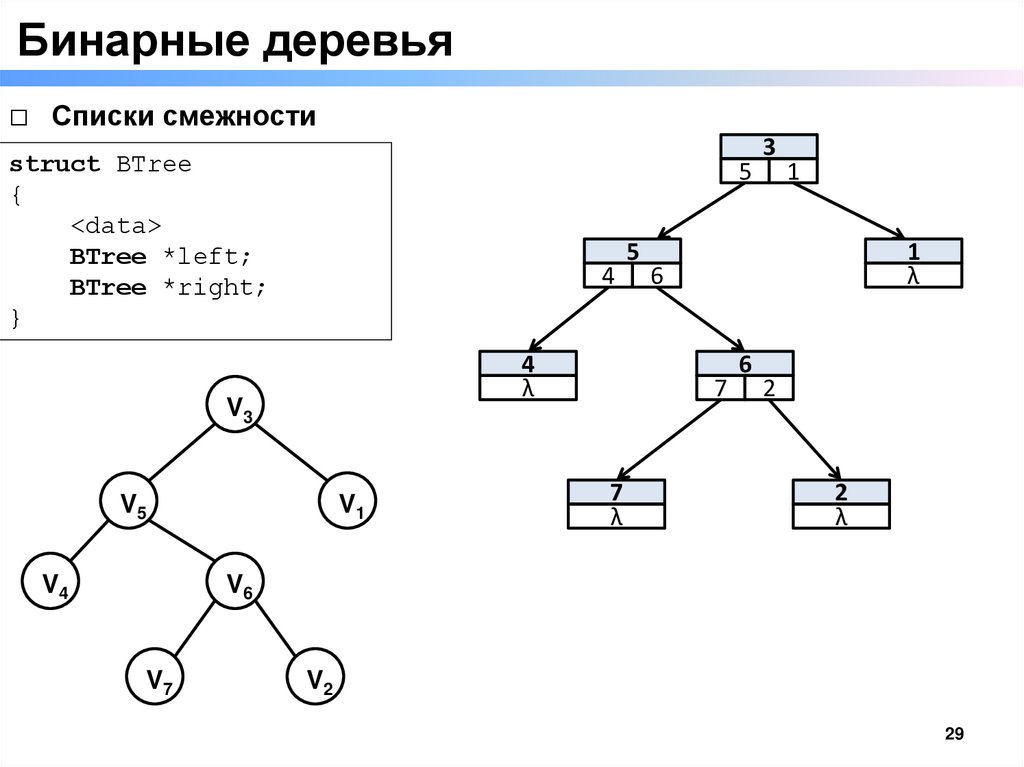
Бинарные деревья
□ Списки смежности
struct BTree
{
<data>
BTree *left;
BTree *right;
}
5
4
4
λ
V3
V5
V4
V1
5
1
1
λ
6
7
7
λ
3
6
2
2
λ
V6
V7
V2
29

30.

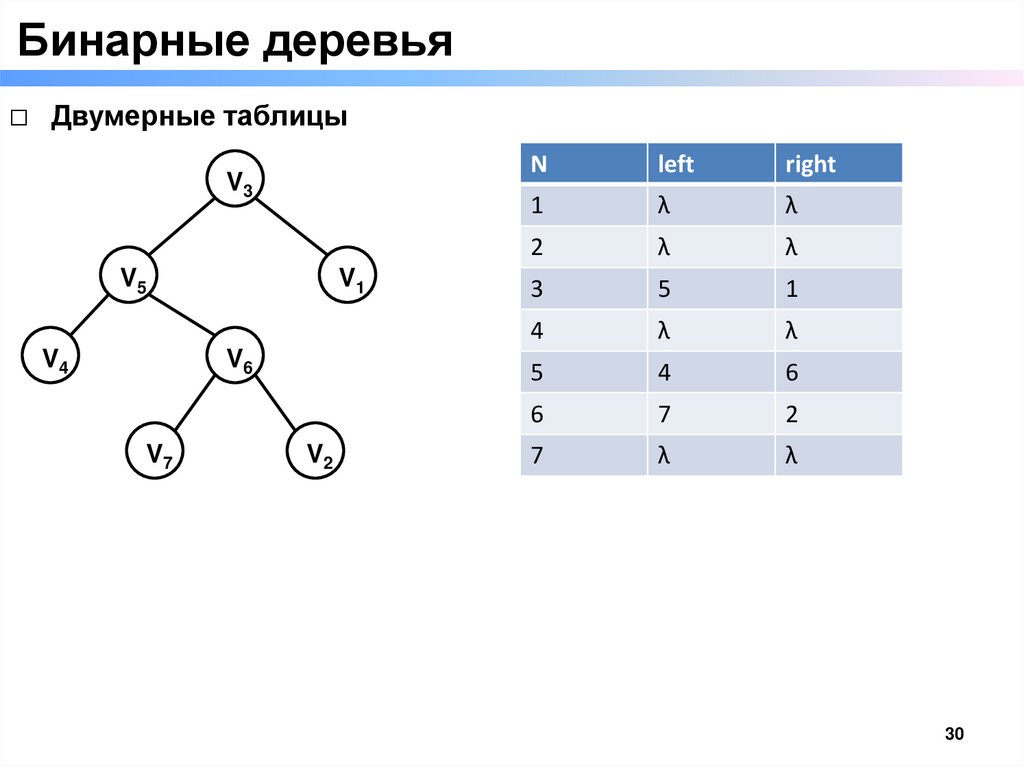
Бинарные деревья
□ Двумерные таблицы
V3
V5
V4
V1
V6
V7
V2
N
left
right
1
λ
λ
2
λ
λ
3
5
1
4
λ
λ
5
4
6
6
7
2
7
λ
λ
30

31.

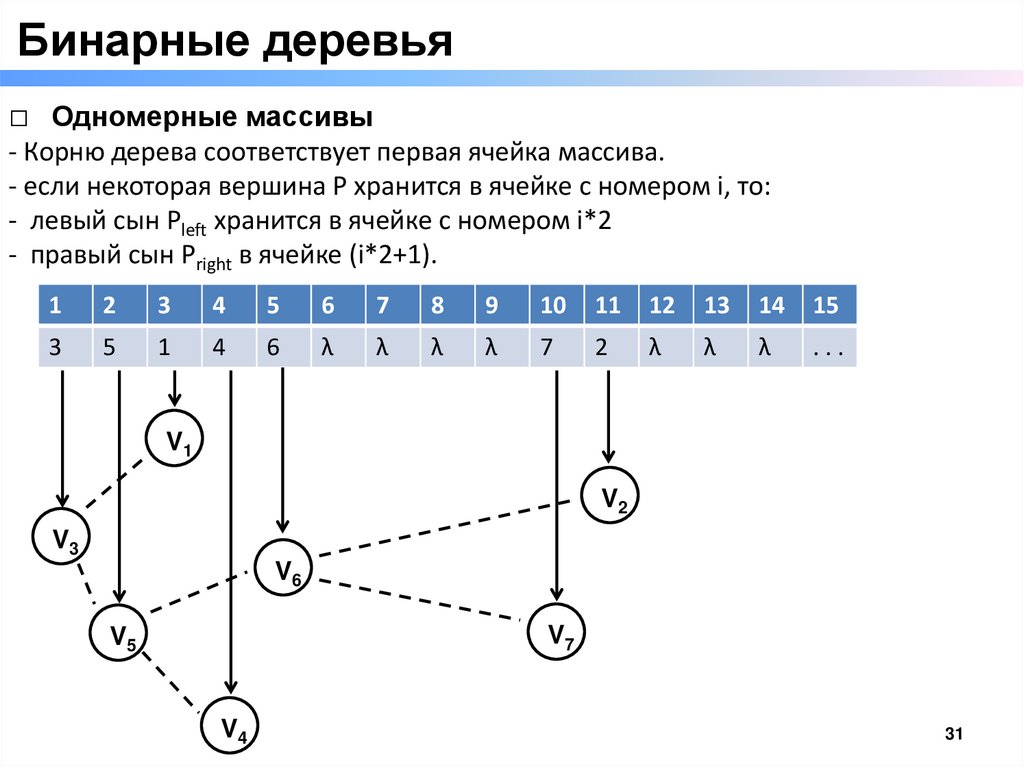
Бинарные деревья
□ Одномерные массивы
- Корню дерева соответствует первая ячейка массива.
- если некоторая вершина P хранится в ячейке с номером i, то:
- левый сын Pleft хранится в ячейке с номером i*2
- правый сын Pright в ячейке (i*2+1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3
5
1
4
6
λ
λ
λ
λ
7
2
λ
λ
λ
...
V1
V2
V3
V6
V7
V5
V4
31

32.

32

33.

33

34.

34

35.

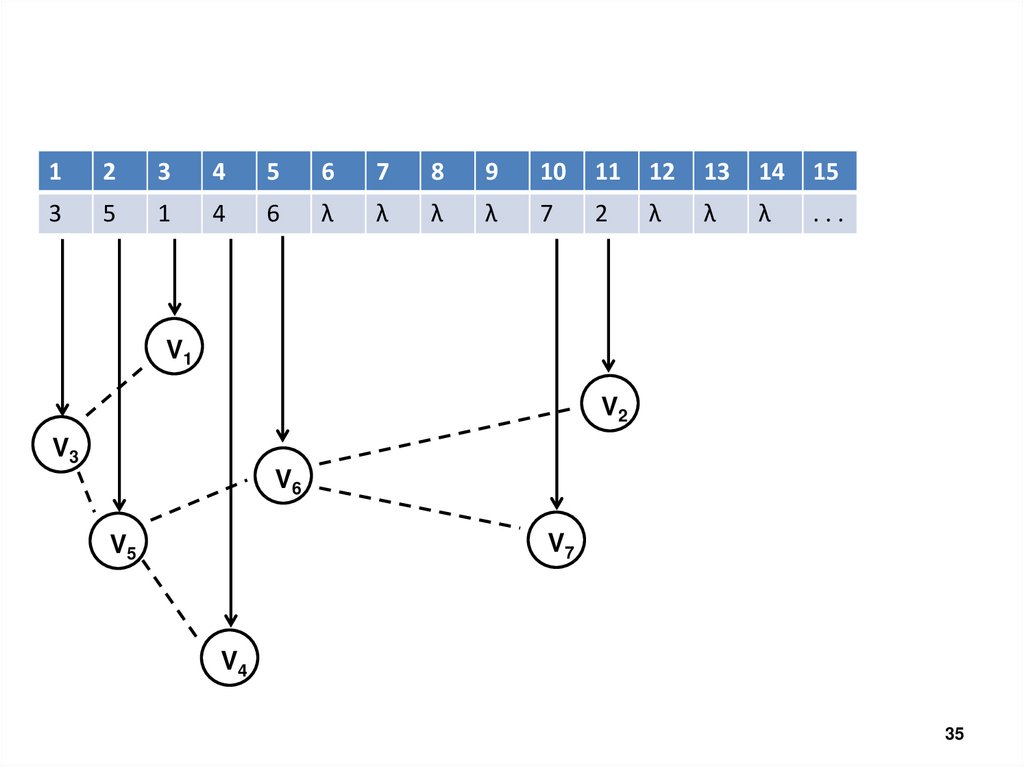
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3
5
1
4
6
λ
λ
λ
λ
7
2
λ
λ
λ
...
V1
V2
V3
V6
V7
V5
V4
35