Лекция 5. Регрессионный анализ

1.

Анализ взаимосвязей географических и
экологических данных.
Регрессионный анализ.
ЛЕКЦИЯ 5
1

2. Цель лекции: изучить основы регрессионного анализа и его реализацию в решении практических естественнонаучных задач

План лекции:
1. Системный подход в географии и экологии.
2. Основы регрессионного анализа
3. Линейные и нелинейные регрессии.
4. Реализация регрессионного анализа
2

3. Начнем с примера из жизни!

Что понимается под
словом «ПОГОДА»?
От чего зависит цена на
квартиру?
ВЫ ТОЛЬКО ЧТО ПРОДЕМОНСТРИРОВАЛИ ПРИМЕР
СИСТЕМНОГО МЫШЛЕНИЯ!
3

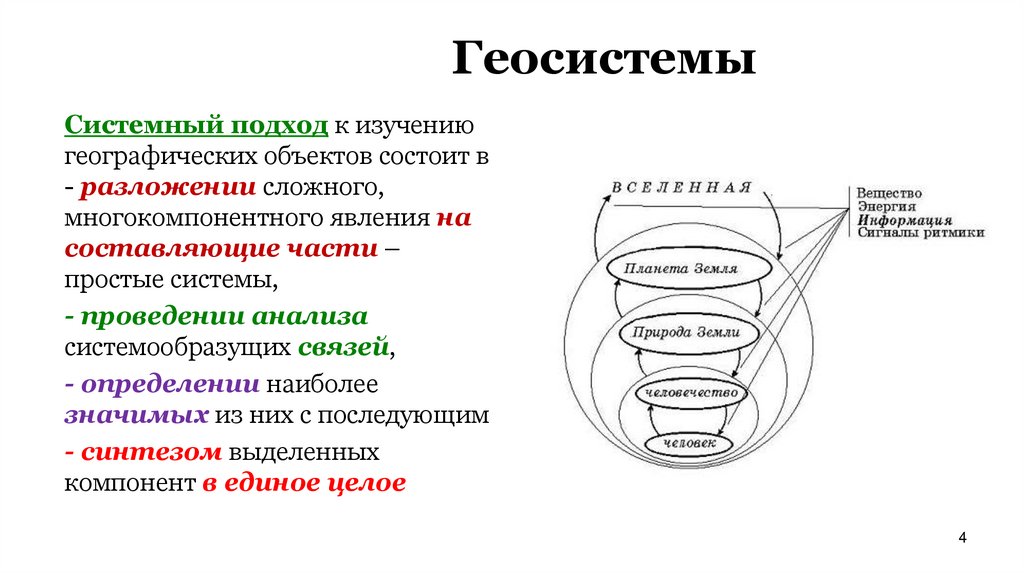
4. Геосистемы

Системный подход к изучению
географических объектов состоит в
- разложении сложного,
многокомпонентного явления на
составляющие части –
простые системы,
- проведении анализа
системообразущих связей,
- определении наиболее
значимых из них с последующим
- синтезом выделенных
компонент в единое целое
4

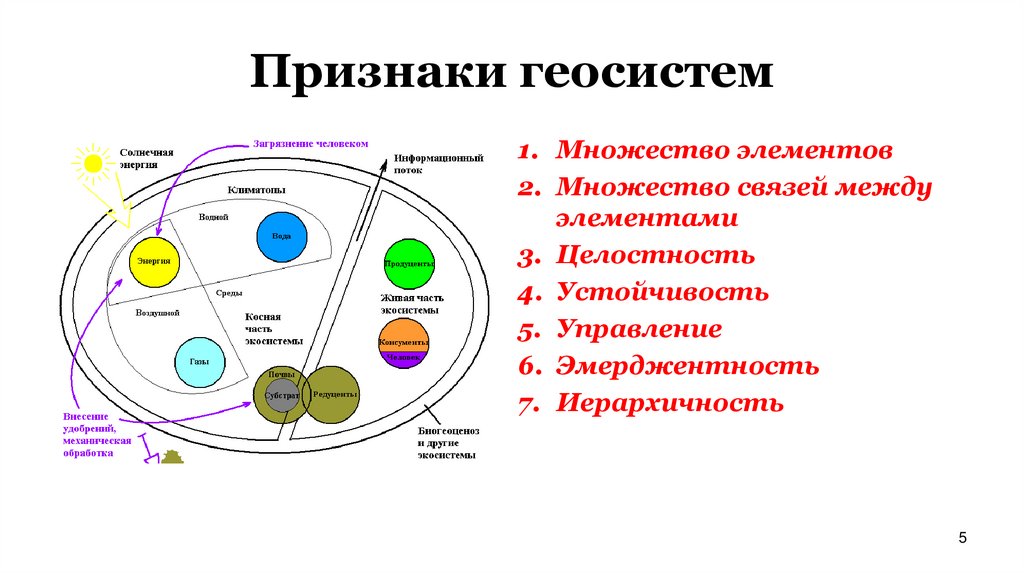
5. Признаки геосистем

1. Множество элементов
2. Множество связей между
элементами
3. Целостность
4. Устойчивость
5. Управление
6. Эмерджентность
7. Иерархичность
5

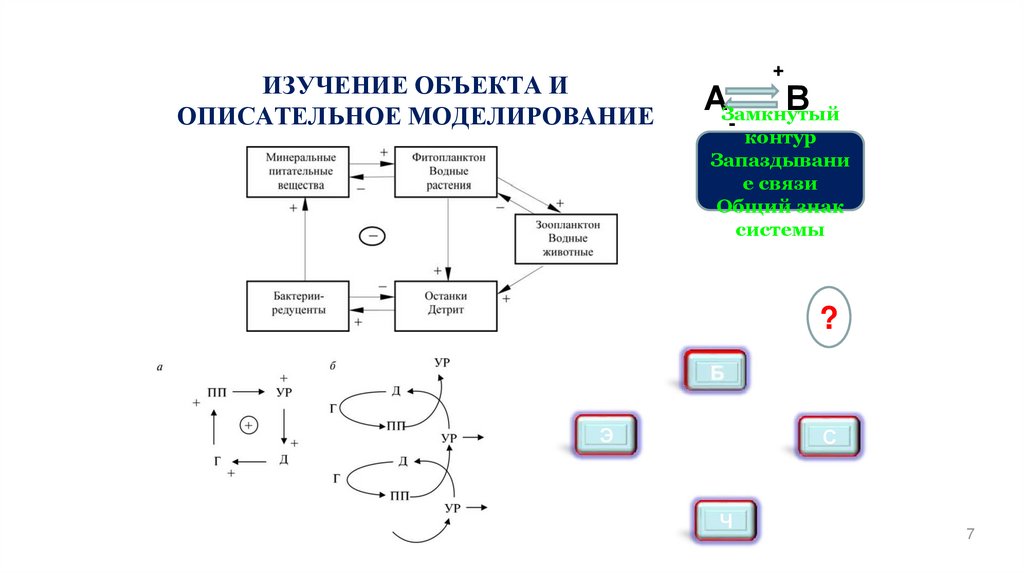
6. ИЗУЧЕНИЕ ОБЪЕКТА И ОПИСАТЕЛЬНОЕ МОДЕЛИРОВАНИЕ

Основные системные понятия
ИЗУЧЕНИЕ ОБЪЕКТА
И ОПИСАТЕЛЬНОЕ
МОДЕЛИРОВАНИЕ
Элементы
Свойства
Состояние
Процесс
Отношение
Параметр
ПРИМЕР «Город»
1. Элементы
Население (молодежь, трудоспособное население, пенсионеры)
Предприятия, малый бизнес (кафе, магазины и проч.)
Бюджет города
Инфраструктура (школы, больницы, дороги, жилой фонд)
2. Свойства (характеристики каждого элемента)
Свойства населения: численность, средний возраст, уровень безработицы
Свойства предприятий: объем производства, численность персонала, рентабельность.
Свойства малого бизнеса: количество рабочих мест, оборот.
Свойства бюджета: доходная часть, расходная часть, дефицит.
Свойства инфраструктуры: износ коммунальных сетей, качество дорог.
3. Параметры («правила игры» для системы)
Ставка налога на прибыль предприятий
Кредитная ставка для малого бизнеса в регионе
Нормативная обеспеченность жильем (м²/человека)
4. Состояние («моментальный снимок» города на дату X)
Состояние на 2020 год:
Численность населения = 50 000 чел.
Уровень безработицы = 15%
Рентабельность комбината = -5%
Миграционный отток = 1000 чел./год
Дефицит бюджета = 20%
Состояние на 2024 год:
Численность населения = 48 000 чел.
Уровень безработицы = 8%
Рентабельность комбината = 2%
Миграционный отток = 300 чел./год
Дефицит бюджета = 5%
5. Процесс (смена состояния системы)
6. Отношение (взаимосвязи между элементами)
Зависимость: бюджет города зависит от налоговых поступлений с предприятий и малого
бизнеса.
Конкуренция: предприятия и малый бизнес конкурируют за трудовые ресурсы
(население).
6
Поддержка: федеральные средства направлены на поддержку инфраструктуры города.

7. ИЗУЧЕНИЕ ОБЪЕКТА И ОПИСАТЕЛЬНОЕ МОДЕЛИРОВАНИЕ

+
АЗамкнутый
В
-
контур
Запаздывани
е связи
Общий знак
системы
?
Э
С
Ч
7

8. Идем дальше!

Мы выяснили, что на цену квартиры сказывается
микрорайон; материал, из которого построен дом; этаж;
природные блага (парки, водоемы и проч.); транспортная
обеспеченность и т .д.
Получается «рой точек». Это причинные факторы.
Но какой из них важнее? Что лучше: жить в 2-х минутах от
остановки или с видом на парк? На 1-м этаже благоустроенного
подъезда или в историческом центре города?
Задача: найти единственную линию, которая наилучшим
образом опишет этот "рой" точек. То есть, пройдет через все
эти хаотичные данные с минимальной общей ошибкой.
8

9.

Регрессия – зависимость среднего значения
какой-либо случайной величины от
некоторой другой величины или нескольких
величин.
Регрессионный анализ – раздел математической
статистики, объединяющий практические методы
исследования регрессионной зависимости между
величинами по данным статистических
наблюдений.
Впервые
термин
«регрессия»
был
введен
основателем биометрии Ф. Гальтоном (XIX в.),
идеи которого были развиты его последователем
К. Пирсоном (1908г.)
9

10.

В ходе регрессионного анализа определяется
аналитическое выражение связи зависимой
случайной величины Y (результативный
признак) с независимыми случайными
величинами
Х1, Х2, …Хm (факторами,
предикторами).
Практически речь идёт о том, чтобы,
анализируя множество точек на графике (т.е.
множество статистических данных), найти
линию, по возможности точно отражающую
заключённую
в
этом
множестве
закономерность,
тенденцию
–
линию
регрессии.
10

11.

Уравнение регрессии - это форма связи результативного признака Y
с факторами Х1, Х2, …Хm. В зависимости от типа выбранного
уравнения различают линейную и нелинейную (квадратичную,
экспоненциальную, логарифмическую и т.д.) регрессию.
В зависимости от числа взаимосвязанных признаков различают
парную и множественную регрессию.
Парная – исследуется связь между двумя признаками
(результативным и факторным).
Множественная (многофакторная) – между несколькими
признаками (результативным и несколькими факторными).
11

12. Последовательность этапов регрессионного анализа

1) Формулировка задачи. На этом этапе формируются предварительные
гипотезы о зависимости исследуемых явлений.
2) Определение зависимых и независимых (объясняющих) переменных.
3) Сбор статистических данных. Данные должны быть собраны для
каждой из переменных, включенных в регрессионную модель.
4) Формулировка гипотезы о форме связи (парная или множественная,
линейная или нелинейная).
5) Определение функции регрессии (заключается в расчете численных
значений параметров уравнения регрессии)
6) Оценка точности регрессионного анализа.
7) Интерпретация полученных результатов. Полученные результаты
регрессионного анализа сравниваются с предварительными
гипотезами. Оценивается корректность и правдоподобие
полученных результатов.
8) Прогноз неизвестных значений зависимой переменной.

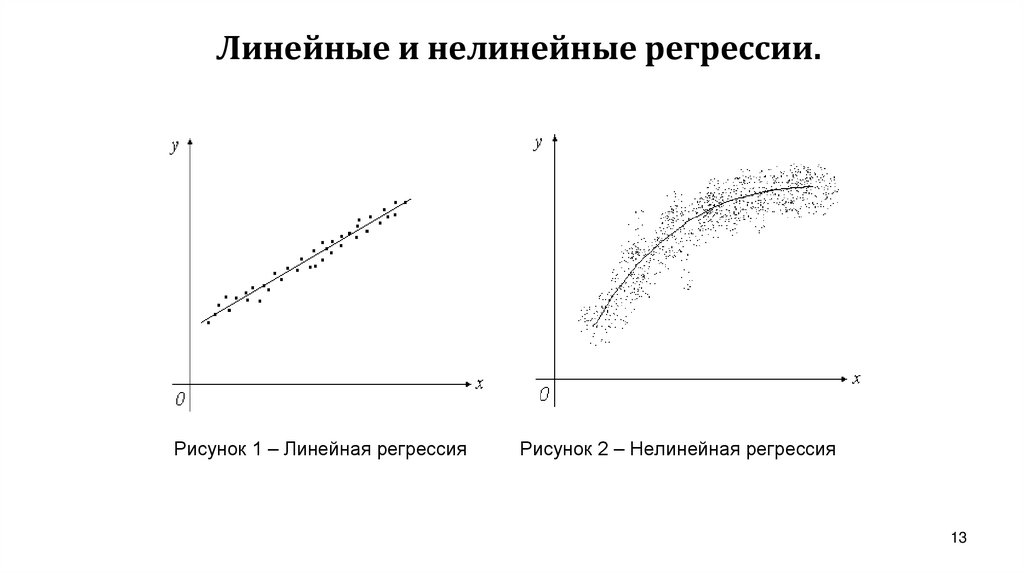
13. Линейные и нелинейные регрессии.

Рисунок 1 – Линейная регрессия
Рисунок 2 – Нелинейная регрессия
13

14. Линейная регрессия

.
МНК
14

15. Метод наименьших квадратов

Параметры уравнения регрессии могут быть определены с
помощью метода наименьших квадратов (МНК)
МНК основан на минимизации суммы квадратов отклонений
эмпирических (фактических) значений результативного признака от
теоретических, полученных по выбранному уравнению регрессии,
т.е.
15

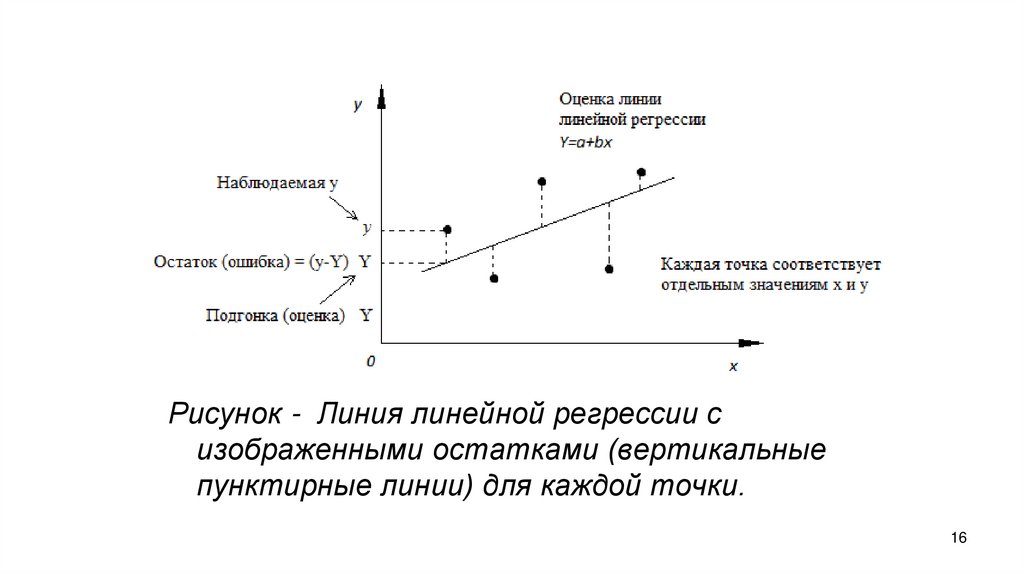
16.

Рисунок - Линия линейной регрессии с
изображенными остатками (вертикальные
пунктирные линии) для каждой точки.
16

17.

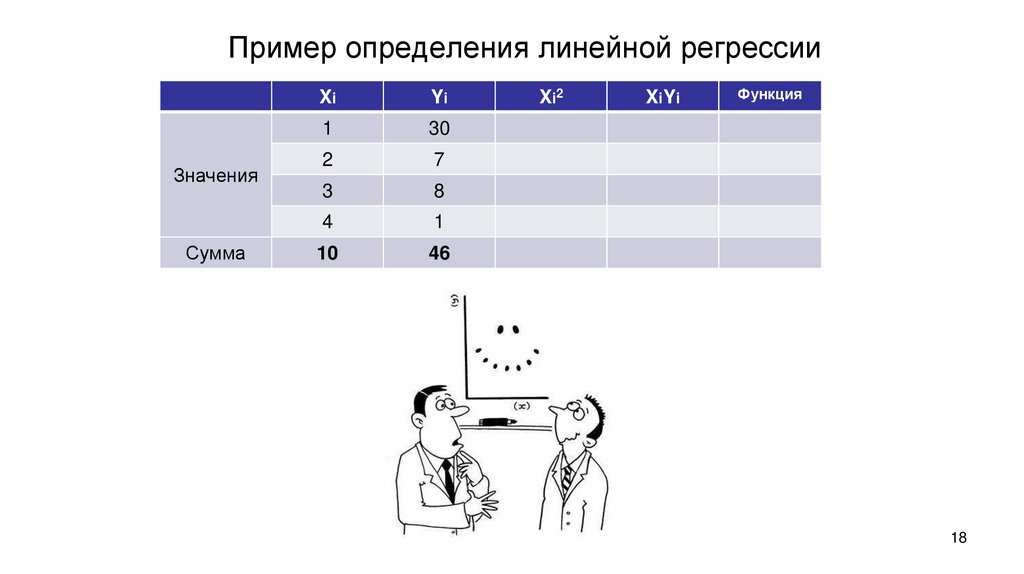
17

18. Пример определения линейной регрессии

Значения
Сумма
Xi
Yi
1
30
2
7
3
8
4
1
10
46
Xi2
XiYi
Функция
18

19. ЗАДАЧА 1.

19

20. Нелинейная регрессия

1) Полиномиальная
2) Гиперболическая
3) Степенная
4) Показательная
5) Экспоненциальная
y b0 eb1x
20

21. Гиперболическая зависимость

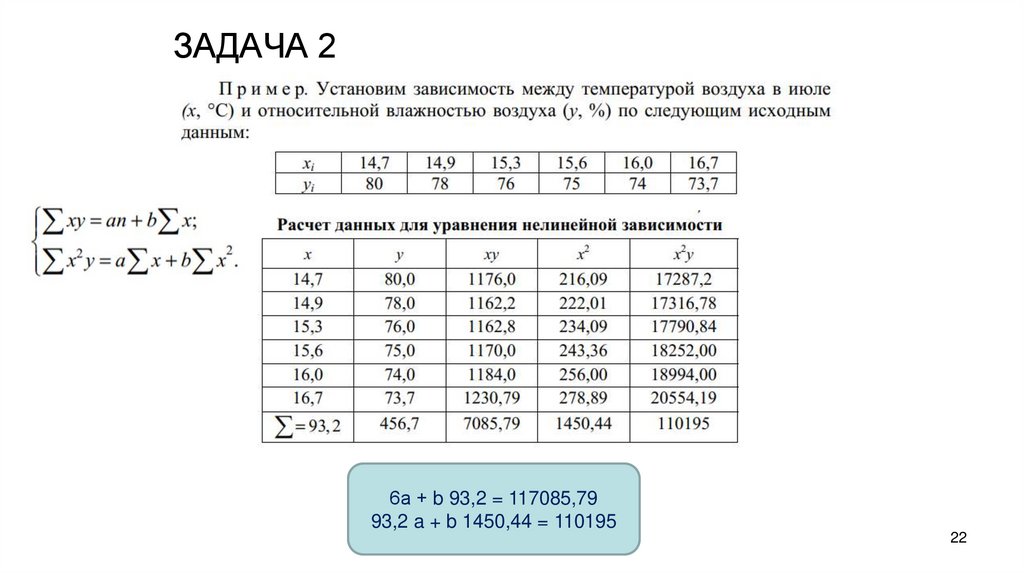
21

22. ЗАДАЧА 2

6а + b 93,2 = 117085,79
93,2 a + b 1450,44 = 110195
22

23. Параболическая зависимость

23

24. Множественная регрессия

Уравнение множественной линейной регрессии
yˆ a 0 a1 x1 a 2 x 2 ... a m x m,
где ŷ – теоретические значения результативного признака,
полученные путем подстановки соответствующих значений
факторных признаков в уравнение регрессии;
x1 , x2 ,... xm – значения факторных признаков;
a0 , a1 ,... am – параметры уравнения (коэффициенты регрессии).
24

25.

y na0 a1 x1 a2 x2 ... am xm ,
2
yx1 a0 x1 a1 x1 a2 x2 x1 ... am xm x1 ,
...
2
yx a
x
a
x
x
a
x
x
...
a
x
.
m
0
m
1
1
m
2
2
m
m
m
Здесь n – число наблюдений, m – число факторов в уравнении
регрессии.
Решение системы позволяет получить значения параметров
регрессии .
25

26. Зависимость от двух факторов

26

27. ОЦЕНКА ТОЧНОСТИ РЕГРЕССИОННОГО АНАЛИЗА Определение ошибки аппроксимации

Для оценки адекватности уравнения регрессии часто также
используют показатель средней ошибки аппроксимации
(величина не более 15% говорит о хорошо подобранном
уравнении)
n
yi yˆ
1
n
i 1
yi
100%.
27

28. ВЕРИФИКАЦИЯ МОДЕЛИ

Верификация – процесс установления
соответствия между численной моделью и
математической моделью.
Y = ax + b
Параметр а называется коэффициентом регрессии, знак
при нем показывает направление связи. Величина
коэффициента показывает, как в среднем изменяется
величина результативного признака при изменении
предиктора на единицу.
28

29. ВЕРИФИКАЦИЯ МОДЕЛИ

Для сравнения оценок роли различных факторов в
форсировании моделируемого показателя может
использоваться показатель:
Средние (частные) коэффициенты эластичности
показывают, на сколько процентов изменится объясняемый
фактор при изменении соответствующего объясняющего
фактора на 1%, при постоянных значениях всех остальных
объясняющих факторов модели.
29

30. Задание для самостоятельной работы

30